一道课后习题的多解与反思*
——对数比较大小问题
福建省福清华侨中学 (350300) 俞文锐
1.引言
对数比较大小问题是每年高考的热点题型,题型杂方法多,重点考查数形结合思想,化归转化思想,以及数学抽象、数学运算、直观想象等核心素养,那么对于底数不同、真数也不同的对数比较大小,究竟要应用什么方法予以解觉呢?本文以人教A版必修第一册一道习题为例对该问题进行探究.
2.试题呈现
例1 比较log23,log34,log45的大小(人教A版数学必修第一册P141拓广探索第13题)
3.解法探究
我们先比较log34,log45的大小.
解法一:(运用作差法+基本不等式比较大小)


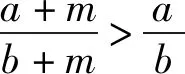
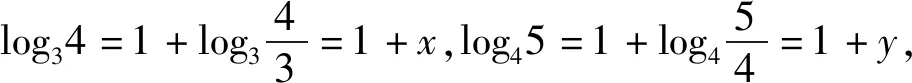
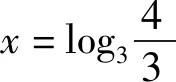

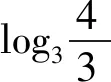

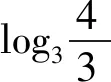

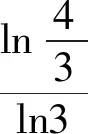
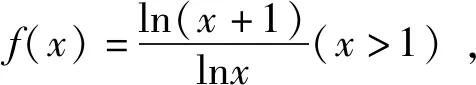
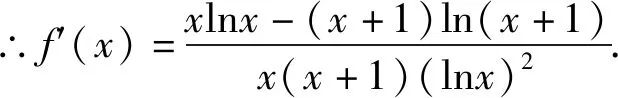
评析:通过构造函数,研究函数的单调性,利用单调性比较大小,也是我们常用的一种策略,解题教学中要给予充分的关注.
4、解题反思
本题中两个对数的底数和真数具有规律性,我们可以将它推广到一般性结论.
性质1 当a>1 时,loga(a+1)>log(a+1)(a+2).
证明:由解法 7 已知结论成立知.
性质2 当 1

性质3 设b>a>1,n>0,m≥1,则有
logam+n(bm+n) 性质4 若1 证明:性质3中取m=1可得性质4. 利用性质1、性质3、性质4我们可以轻松获得log23>log34>log45,对于底数、真数呈现以上规律性的对数我们可以快速比较大小,那么对于任意的底数不同、真数也不同的对数比较大小问题,我们能否获得一般性的结论呢? 例1 (2013年全国Ⅱ卷第8题)设a=log36,b=log510,c=log714,则( ). (A)c>b>a(B)b>c>a (C)a>c>b(D)a>b>c 例2 (2020年全国卷3理科第12题)已知55<84,134<83.设a=log53,b=log85,c=log138,比较a,b,c的大小. 结语:比较大小问题是经典的题型,教材中蕴含有多种解题方法,如作差法、构造法、单调性法、基本不等式法、不等式性质法、分析法、中间量法、图像法等,充分挖掘教材中的解题方法,通过一题多解教学,培养学生的数学运算能力,促进数学思维的发展,培养学生发散性思维能力,同时也让学生进一步体会到不同知识之间的紧密联系.通过对习题的拓展,学生依据从特殊到一般的推理,从特殊的命题log34>log45出发,得到一般性的命题:若b>a>1,n>0,m≥1,则有logam+n(bm+n)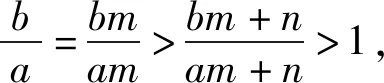

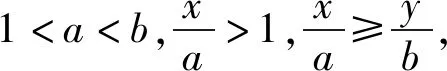
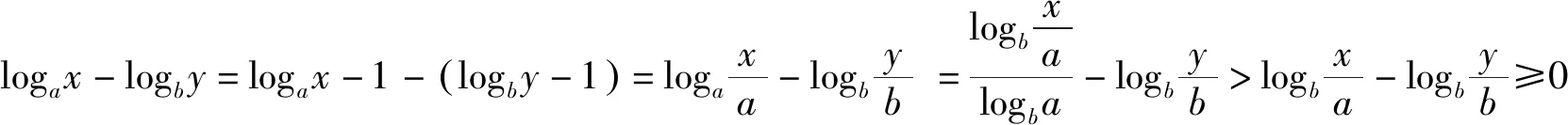
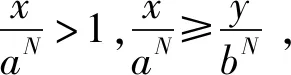
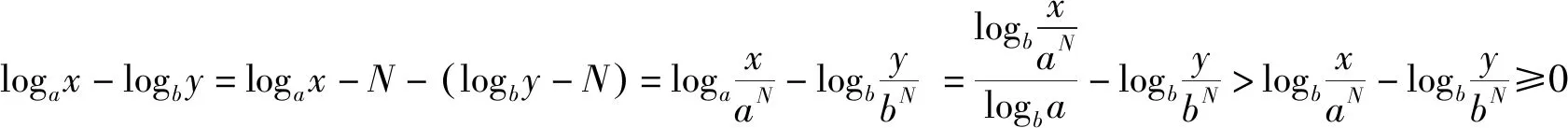
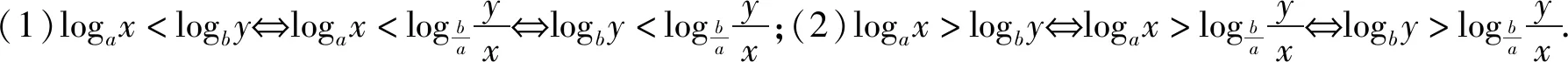
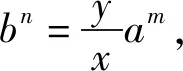
5、高考真题链接