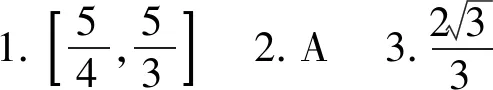一道联考试题的命制背景探究与求解
山东省宁阳县复圣中学 (271400) 张志刚
一、题目呈现
(2020高考浙江省3月联考(B)第10题)已知实数x,y,满足x2-4xy-5y2=5,则x2+2y2的最小值为( ).
二、命制背景
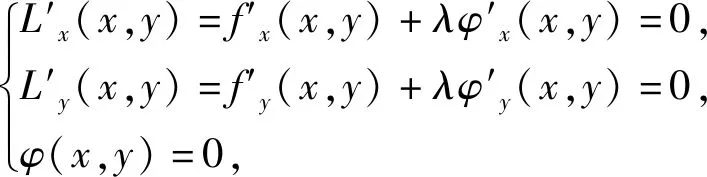

图1
拉格朗日乘数法的优点主要有两点:一是把目标函数和等式约束统一到一个拉格朗日函数中;二是将条件极值问题转化为无条件极值问题,即通过引入拉格朗日乘数来将含有n个变量和k个约束条件的约束优化问题转化为含有n+k个变量的无约束优化问题.因为在构造的拉格朗日函数中无论约束条件φ(x,y)=0如何,都满足限制条件.另外,L(x,y)=f(x,y)+λφ(x,y),其中φ(x,y)=0,不难发现求z=f(x,y)的极值点,其实就是求L(x,y)的极值点,两者的极值是等价的,且与λ无关,至于为什么增加一个λ,其实就相当于用待定系数法来确定这个拉格朗日函数.拉格朗日乘数法能够保证在取得最优乘数的情况下两者解的一致性,显然通过求解拉格朗日函数的最优解来求得原目标函数的最优解是一种更实际,更方便的做法.于是,我们可以用这种方法来破解一些简单的条件极值问题,例如本题可解答如下:
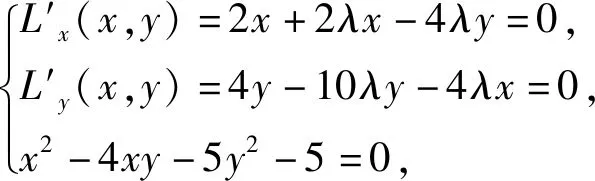
三、题目解答
拉格朗日乘数法作为一种应用广泛的约束问题优化算法,其理论上的优越性显而易见.然而,在实际操作中,对拉格朗日乘数法求极值的原理理解接受需要一个过程,求偏导对于高中学生来说也是陌生的,另外,在联立方程组求解时对学生运算求解能力要求较高,那么,本题如何用初等数学的方法解决呢?事实上,在高中阶段,解决此类问题可以分别从基本不等式、方程有解、函数最值(三角代换或导数)等途径寻求突破,消参减元转化是这类问题的基本解题原则,把双变量问题转化为一元函数或方程,再辅以相应的数学知识和方法就能解决.当然,鉴于该类题目的综合性,解答过程往往需要考生具备较高的数学抽象、逻辑推理、数学运算、直观想象等核心素养,转化与化归、函数与方程、分类讨论、换元法、配方法等典型数学思想和方法,颇具挑战性和选拔性.
思路一:换元法+基本不等式法
通过观察已知条件x2-4xy-5y2=5,可以发现,该等式可以通过因式分解等价变形为(x-5y)(x+y)=5,由“积为定值”的结构特征,联想到进行换元s=x-5y,t=x+y,从而将关于x,y的二元函数转化为s,t的二元函数,进而借助基本等式求出最值即可.
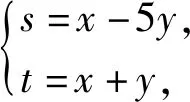

思路二:判别式法
转化为方程有解利用判别式△≥0也是处理该类试题的常见思路.利用目标函数构造二次的齐次式,分子、分母同时除以x2(或y2),借助换元法将二元方程转化为一元二次方程有解问题,利用判别式△≥0求解,于是有了如下解法.
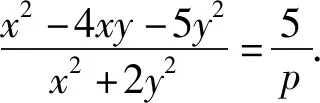
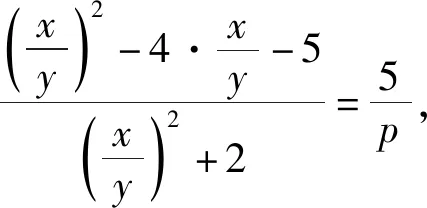
思路三:三角换元法
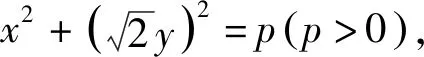
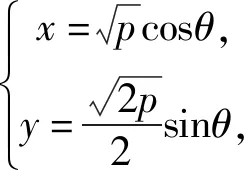

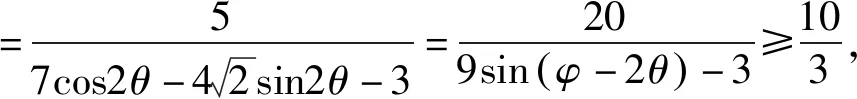
评注:使用三角代换,把双变量问题转化为单变量问题,利用正余弦函数的有界性,求平方和代数式的范围是常用方法和思路.
思路四:导数法
与思路二类似,利用目标函数构造齐次式,然后分子、分母同时除以x2(或y2),换元后将目标函数转化为分式函数的最值问题,然后通过导数方法研究函数的单调性,进而求出极值和最值.
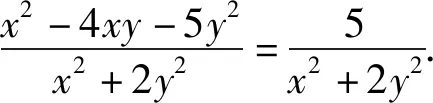
①当y=0时,x2+2y2=x2=5;


图2
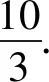
思路五:配凑法+平方非负性
通过观察、配凑,变形为完全平方公式形式,利用完全平方非负性,确定最值.
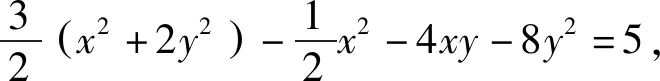
追根溯源可以让我们了解命题意图,横跨纵联也利于培养学生的发散思维.以拉格朗日乘数法为背景的二元二次方程条件下的二元最值问题,历来是高考和竞赛的热点和难点问题,题目一般是函数、方程与不等式知识的综合应用试题,解法多样,活泼灵动,技巧性较强.当然,在解题过程中,要防止没有思想的技巧,或者说揭示不出技巧背后的思想的做法是不可取的,违背了数学教育的育人之道,把数学变成了形式化的技巧.作为教师,一定要把技巧后面的思想挖掘出来,充分体现教学的简约性功能.
最后,读者可仿照上述方法求解以下三题.
1.(2020届浙江省宁波市高三期末考试)已知45x2-12xy+52y2=20,求3x2+4y2的范围.
2.(2017年清华大学中学生标准学术能力测试第12题)已知实数x,y满足5x2-y2-4xy=5,则2x2+y2的最小值是( ).
3.(2016年全国高中数学联赛甘肃赛区预赛第1题)若实数x,y满足x2+y2+xy=1,则x+y的最大值是.