从一道高考题再谈“类周期函数”
上海市上海中学东校 (201306) 汪海鹏
函数性质问题是高考和竞赛中常见的题型.周期性是函数的重要性质,很多题目中会出现周期函数的影子—与周期函数类似的函数,我们称之为类周期函数.这种题目在竞赛和高考中变化多样,形式新颖,可以很好的考查学生的数学综合素养,备受命题人青睐.
一、考题再现
题目(2021年上海高考21题)如果对任意x1,x2∈R使得都有x1-x2∈S,则称f(x)是S关联的.
(1)判断并证明f(x)=2x-1是否是[0,+∞)关联?是否是[0,1]关联?
(2)f(x)是{3}关联的,在[0,3]上有f(x)=x2-2x,解不等式2≤f(x)≤3;
(3)“f(x)是{1}关联的,且是[0,+∞)关联”当且仅当“f(x)是[1,2]关联的”.
该题目巧妙的在新定义的情景当中融入了类周期函数的性质,(2)、(3)中的“f(x)是{3}关联的“和”f(x)是{1}关联的“就可以看作类周期函数的综合问题.破解题目的关键就是结合题目中的新背景,通过分析类周期函数的性质和图像即可明确清晰.而(3)中的“不等式”型类周期问题的解决要求更高了,还考查到学生的不等式相关知识,以及其他数列思想,思维含量比较高,是体现数学能力的很好载体.
二、问题破解
解法1:(1)①设任意x1,x2∈R,且x1-x2∈[0,+∞),则f(x1)-f(x2)=2x1-1-2x2+1=2(x1-x2)∈[0,+∞),f(x)=2x-1是[0,+∞)关联的.
②设x1-x2∈[0,1],f(x1)-f(x2)=2x1-1-2x2+1=2(x1-x2)∈[0,2],故f(x)=2x-1不是[0,1]关联的.
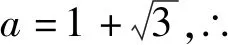
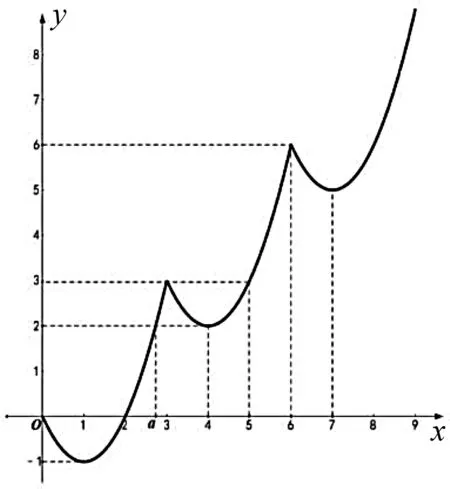
图1
(3)充分性:由f(x)是{1}关联的可知,对任意x∈R,函数f(x)满足f(x+1)-f(x)=1.由f(x)是[0,+∞)关联的可知函数f(x)单调不减.
设任意x1,x2∈R,且1≤x1-x2≤2,一方面f(x1)-f(x2)≥f(x2+1)-f(x2)=f(x2)+1-f(x2)=1,另一方面f(x1)-f(x2)≤f(x2+2)-f(x2)=f(x2)+2-f(x2)=2.即得f(x1)-f(x2)∈[1,2].
必要性:∵f(x+1)-f(x)≥1,f(x+2)-f(x+1)≥1,f(x+2)-f(x)≤2可以得到f(x+1)=f(x)+1.故对x
点评:(2)中函数类周期性质中,当自变量从一个周期变化到下一个周期时,其函数值发生了变化,其图像同时发生了左右平移和上下平移,解决此类问题的关键时抓住函数在主值区间上的图像,由此延拓到整个定义域上,从图像中找出规律,然后尝试离开图像,直接从局部解析式中得到整个解析式,求得问题的解.(3)中“不等式”型类周期问题的解决要求更高,它不但考查有关函数的知识,还要求学生具备不等式相关知识.
解法2:(1)x1-x2∈[0,+∞),f(x1)-f(x2)=(2x1-1)-(2x2-1)=2(x1-x2)∈[0,+∞),f(x)=2x-1是[0,+∞)关联;x1-x2∈[0,1],f(x1)-f(x2)=(2x1-1)-(2x2-1)=2(x1-x2)∈[0,2],f(x)=2x-1不是[0,1]关联.

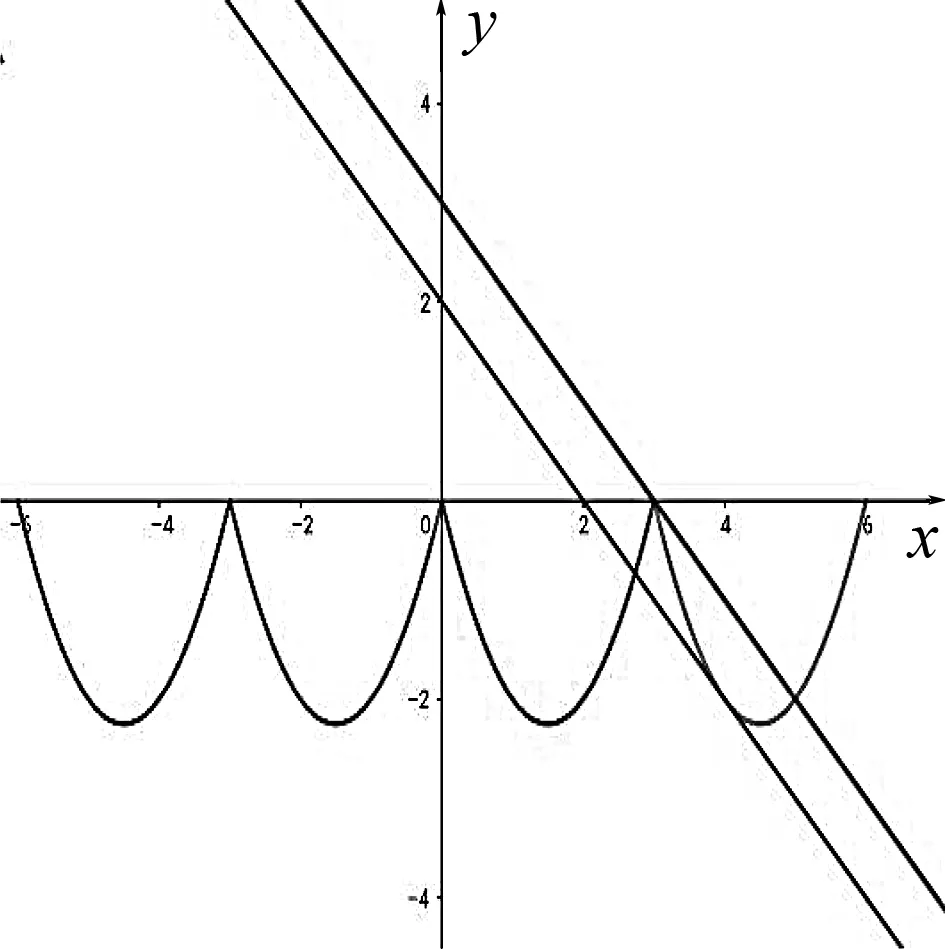
图2
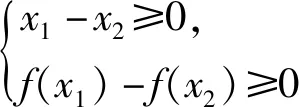
②当f(x)是[1,2]关联,有Δx∈[1,2],∴g(Δx)=f(x+Δx)-f(x)∈[1,2],当g(1)=f(x+1)-f(x)∈[1,2],g(2)=f(x+2)-f(x)∈[1,2]时,假设g(1)>1,有f(x+1)-f(x)>1.∴f(x+2)-f(x)>f(x+1)+1-f(x)>2,又∵g(2)=f(x+2)-f(x)∈[1,2],矛盾.故只有g(1)=1,易得g(2)=2.利用f(x+1)-f(x)=1得f(x)是{1}关联,依次可得g(n)=n,n∈Z+,即当Δx∈[n,n+1],有g(Δx)∈[n,n+1],当n→+∞时,Δx∈[0,+∞),g(Δx)∈[0,+∞).
点评:结合已知条件中定义的抽象函数的性质,利用化归思想,结合周期数列的处理方法,巧妙将题中的条件有效转化.
三、变式拓展
通过改变真题中类周期函数的形式,由平移型改为伸缩型或者为不等式型,合理改变给出函数类周期的条件,会得到以下相应的类似问题.
变式1 我们把定义在R上,且满足f(x+T)=af(x)(其中常数满足a≠1,a≠0,T≠0)的函数叫做类周期函数.
(1)当T=1,a=2时,某个类周期函数在0≤x<1时的解析式为f(x)=x2-2x,求函数y=f(x),x∈[n,n+1),n∈Z的解析式;
(2)对于确定的T>0且0 解析:(1)类周期函数在0≤x<1时的解析式为f(x)=x2-2x,当x∈[n,n+1),n∈Z时,x-n∈[0,1),则f(x)=2f(x-1)=22f(x-2)=…=2nf(x-n)=2n[(x-n)2-2(x-n)],所以f(x)=2n[x2-(2n+2)x+n2+2n],x∈[n,n+1),n∈Z. (2)类周期函数T>0且0 解析:由f(x)+2017≤f(x+2017)=f(x+1+2016)≤f(x+1)+2016可得f(x)+1≤f(x+1),同理由f(x)+2016≥f(x+2016)递推可知f(x)+1≥f(x+1),从而f(x)+1=f(x+1),进而知{an}是等差数列.a2018=a1+2017=2019. 类周期函数问题是函数综合知识考察类型的常青树,对这类问题的探究是基于周期函数的基础上,对函数性质作更深入的挖掘,它要求学生具有比较全面的函数基础知识,具有类比分析、数形结合等解题思想能力,是高考和竞赛试题中的难点,对学生有很好的考察功能.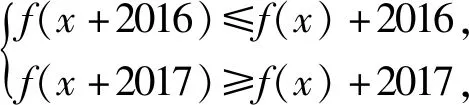
四、解后反思

