对2018年全国Ⅰ卷第21题的本质探究

四川外国语大学附属外国语学校 (400000) 郭海峰

2018年全国Ⅰ卷第21题考察了函数、导数以及不等式等知识，该问题考察了分类讨论、数形结合和等价转化等数学思想，全方位考察了学生的观察、分析、推理论证、运算求解等能力，体现了逻辑推理以及直观想象等核心素养.已经有很多文章讨论过该问题，本文将从“极值点偏移”的角度对该问题进行分析.

一、“极值点”偏移的理论基础

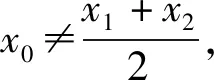
图1 极值点左偏

图2 极值点右偏

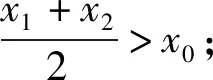
上述结论即是在探讨x1，x2，x0满足算术平均的关系时，探讨对应的函数值之间的关系.除了此类关系外，当x1，x2，x0满足其他关系时，对应的函数值是否有类似的关系呢？2018年新课标Ⅰ卷第21题即是属于此类问题，现将探究过程展示如下：

二、真题展示

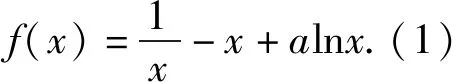
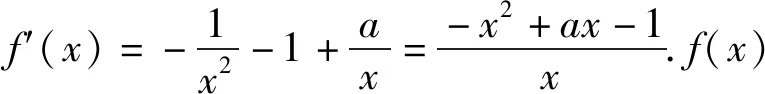
三、解法呈现

(1)构造函数，利用单调性进行判断

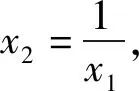
(2)利用对数均值不等式

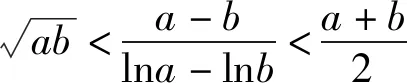
四、解法背景探究

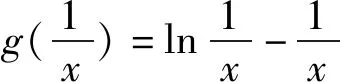
具体如图3所示，利用对称性构造出来的部分位于原函数的下方，由此即可得所证不等式成立；根据图像，我们还可得如下命题，对于函数g(x)=lnx-x，若g(x1)=g(x2)，则可得x1x2<1.同理可得，若对称过来的图象在原函数的上方，则获得相反的答案.

图3

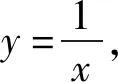
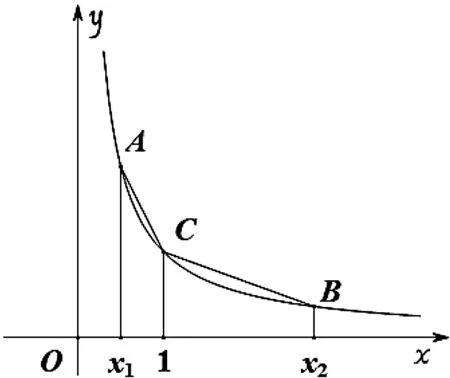
图4