深入探究,豁然开朗
——由一道解三角形题是否两解引发的思考
扬州大学附属中学 (225000) 胡丽媛
在近日的一次练习中,笔者选了2013年北京高考理科卷中的解三角形题,主要考查正弦定理、余弦定理在解三角形中的应用.本认为这是一道容易的解答题,但在批阅过程中发现不少学生产生了两解,为此,笔者进行了一些深入的探究与同行交流.
一、问题呈现
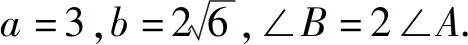
(1) 求cosA的值;(2) 求c的值.
二、解答过程
首先,给出参考答案:
部分同学对第(2)问解答如下:
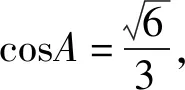
三、深入分析
对于上述解法二,不少采用这一思路的同学是缺失检验,即产生了两解.这不免让我们提出疑问:在三角形已知两条边及其中一边的对角的条件下,若运用余弦定理求第三条边,需要解一元二次方程,那么在出现两个不等的正数解时,是否都要思考“增解”问题呢?
而事实并非如此,分析如下:已知△ABC的两边a,b和一边的对角A,解三角形时,如果A为锐角,那么,可能出现以下情况.
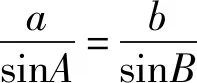
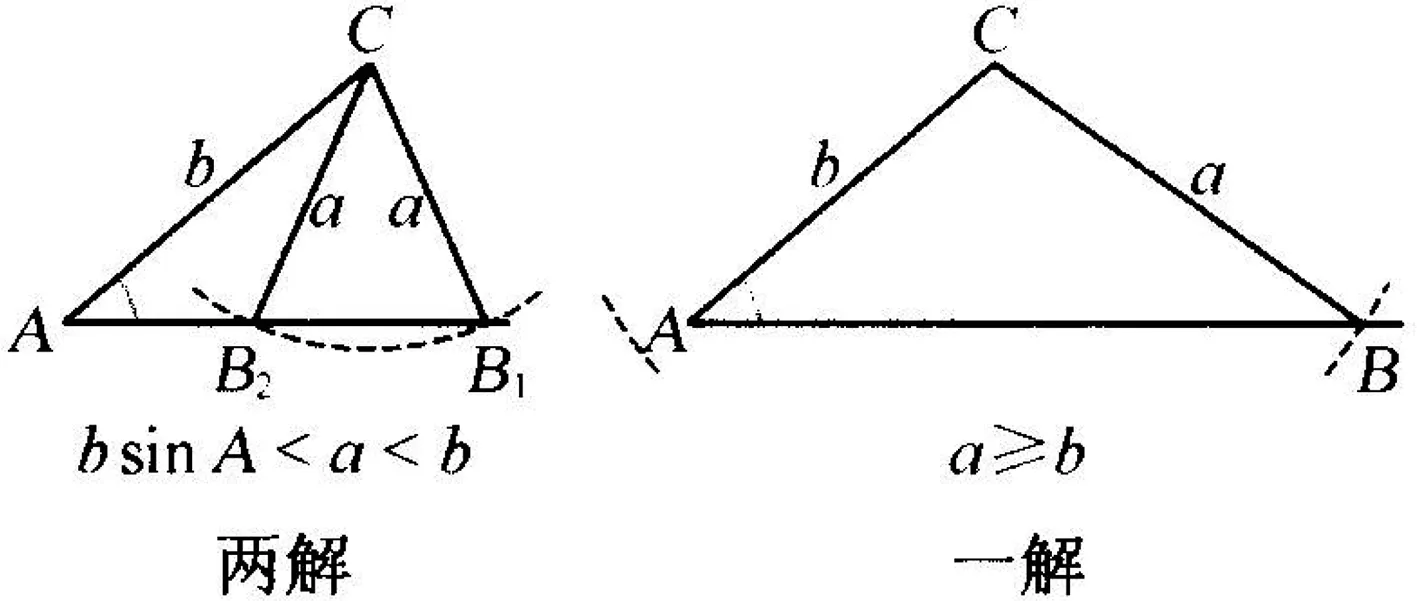
①当sinB>1,即a 图1 图2 ②当sinB=1,即a=b·sinA时,角B有一解,即三角形只有一解,如图2; ③当sinB<1,即a>b·sinA时,角B有锐角和钝角两种可能,由于角A是锐角,故角B能否为钝角决定了三角形解得个数.其中当a≥b,即A≥B时,角B有一解,即三角形只有一解,如图4;当a 图3 图4 那么,如果用余弦定理解出边长c,三角形解的个数情况如何呢? 这些结论显然与正弦定理所得结论是一致的.但这不免让我们产生质疑:已知“边边角”,由余弦定理得出的边长c,会不会不满足三角形成立的条件? 综上所述,当方程(*)有正根时,必然满足三角形成立的条件. 经过前面的分析得知,已知两边及其中一边的对角(锐角)解三角形时,使用余弦定理求解第三条边只要能解出正数解,则不需要作任何验证,那么本题中出现增解的原因究竟是什么呢? 由这题“增解”产生原因的分析,并不是因为运用余弦定理解一元二次方程产生了“增根”,应考虑使用余弦定理之前的条件的得出,是否“不可逆”.学生受知识背景、思维方式等因素的影响,在很多问题上会产生与教师预设不同的想法,而教师在很多时候也会受固定思维的影响,解法二的出现是练习中学生给出的,在出现了“增解”这样的体验之后,如果简单地告知学生避免使用余弦定理解这类题目,无疑是不合适的.学习数学,需要数学思维,可以说,数学的本质特性就是思维,通过对推理过程的严密分析,不仅能解决疑问,也是在帮助学生培养数学思维,让学生经历产生问题、分析问题、解决问题的过程,培养深入思考的习惯.作为教师,不能因固定思维的影响而停滞不前,只有自身做到对问题的“深入”,才能做到在学生面前的“浅出”,才能帮助学生更深刻的理解所学知识.
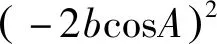
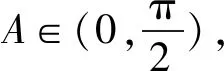
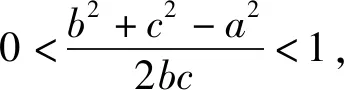
四、揭示错因
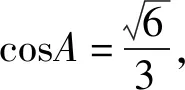
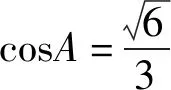
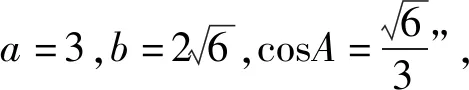
五、反思小结

