从“鸡兔同笼”问题看小学数学建模

黄家平

[摘 要]小学生处于具体运算阶段，对知识的理解要靠直观的形象支撑。学生对知识的学习与掌握，一方面是将知识转化为数学模型的过程，另一方面是对数学知识给予实际意义，还原成贴切的生活情境后，再利用对生活情境的理解来理解数学知识。因此，小学阶段的数学模型具有双面性，可以循环往复建构。

[关键词]数学建模;鸡兔同笼;信息提炼;归纳概括

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）08-0084-03

在小学数学教学中渗透模型思想，可以帮助学生将抽象的数学知识转化成直观的表象，建立经典的数学模型，与相关知识相结合。当学生接触相关知识时，就会不由自主地浮现出与之配对的模型，进而通过对模型的直接经验来反推数学理论，最终掌握数学知识的本质。数学模型思想，就是先将同类数学问题归纳概括出其主要特征，再根据主要特征将解答流程和分析步骤全部设计成固定程序，形成专门应对这类问题的解法。这样一来，就把问题改建成了模型，凡是结构与原理相似的所有题型都可以运用这种方法解决，这一过程我们称之为数学建模。现以小学数学中的“鸡兔同笼”问题为例，谈一谈如何培养小学生的建模意识。

一、对比教材，追根溯源

众所周知，“鸡兔同笼”问题的模型是二元一次方程组，这是到中学才涉猎的内容，然而，“鸡兔同笼”问题却编排在小学教材中。北师大版第九册“尝试与猜测”这一章节中，主要借“鸡兔同笼”问题讲授列举法。苏教版第十一册仅仅将“鸡兔同笼”问题变为一道练习题，借机传授“假设和替换”的解题策略。以上两版教材都只是将这部分内容作为案例或是以练习的形式编入教材中。人教版第八册的“数学广角”将“鸡兔同笼”问题作为一个独立的章节，教材对问题的来源、基本解法及应用范围解释得很详细。而北京版则分两次编排，第一次在第八册，主要介绍图表法，只是触及问题的表层，算是小试牛刀，虽然没有直接推出算式法，但是已经做好了足够的铺垫和预设，算法呼之欲出;第二次安排在第九册，提出方程思路，让“鸡兔同笼”问题借助方程模型完美诠释。

追根溯源，“鸡兔同笼”问题来源于《孙子算经》一书：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”这道趣味数学题对小学生来说，是否存在建模的可能？试想，如果在教学时，我们照本宣科，就题论题，那么学生的思维将很难得到发展，学生也很难掌握“鸡兔同笼”问题的精要所在。我们不妨通过问题的来源激发学生的兴趣，引发学生探究的强烈动机，再揭示课题，最终渗透建模的数学思想。

二、分层建模，从“头”算起

【例题1】一个铁笼里关着红腹锦鸡和荷兰侏儒兔若干只，从上面看有3个头，从下面看有8条腿，红腹锦鸡有几只？荷兰侏儒兔有几只？

由于题目中的头数和腿数均较少，因此教师可这样引导：“你们猜测一下，红腹锦鸡和荷兰侏儒兔各有几只呀？猜测的依据是什么？阐述一下自己的依据。”然后留出充裕的时间让学生深入思考。

生：红腹锦鸡有2只，荷兰侏儒兔有1只。因为1只红腹锦鸡有2条腿，那么2只红腹锦鸡就有4条腿，还剩4条腿，所以只有1只荷兰侏儒兔。

【例题2】一个铁笼里关着红腹锦鸡和荷兰侏儒兔若干只，从上面看有6個头，从下面看有20条腿，红腹锦鸡有几只？荷兰侏儒兔有几只？

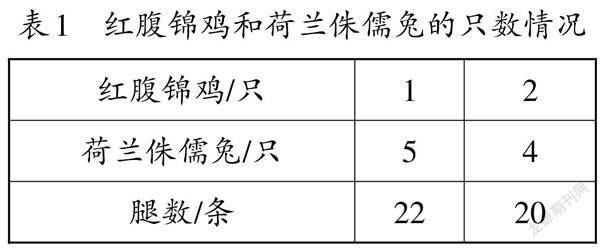
此时要求学生可以猜测推理，可以画图推导，也可以列出算式计算，或直接用算术法。相比例题1，例题2的各项数据变大了，可有些学生还是依赖于猜测推理，以6个头为前提，从1只红腹锦鸡和5只荷兰侏儒兔开始推演，不断调整鸡、兔的数量，直到腿数符合要求为止;有的学生则采取居中原则，将鸡、兔的只数平分，从3只红腹锦鸡和3只荷兰侏儒兔起算;有的学生则从1只荷兰侏儒兔和5只红腹锦鸡开始算，并列出表格（如表1）。

有的学生直接用画图（如下图）的方法把6个头都看成是红腹锦鸡的头，或把6个头都看成是荷兰侏儒兔的头。

这时，教师沟通了列表法和画图法之间的联系——形式不一，但是内涵和原理是一致的，都采用了假设法。借助学生的图示，初步形成解决这类问题的策略，于是教师制订粗略的解题程序。

（1）将所有的动物全部看成红腹锦鸡或荷兰侏儒兔，算出虚拟腿数。

（2）与实有腿数比较，算出差额。

（3）根据腿数的差额，在头数保持不变的前提下，给某几只动物增减腿数，使其变成另一种动物。

（4）确定最终数量，求出红腹锦鸡和荷兰侏儒兔各几只。

【例题3】一个铁笼里关着红腹锦鸡和荷兰侏儒兔若干只，从上面看有8个头，从下面看有26条腿，红腹锦鸡有几只？荷兰侏儒兔有几只？

要求学生自选方法，独立解答。由于学生已经有了列表法和画图法作为架子，建立了稳固的表象，后有方法沟通建立了统一的认识，概括提炼出了假设的基本思路，因此在解答例题3时，算术法已经呼之欲出，顺理成章。此时学生不仅能列出正确的算式，而且对算理也说得头头是道。

生：假设全是红腹锦鸡，那么腿有8×2=16（条），腿数相差26-16=10（条），4-2=2（条），荷兰侏儒兔有 10÷2=5（只），红腹锦鸡有 8-5=3（只）。

教师通过三个层次的逐步推进，数据由小变大，难度逐渐升级，方法由初级到高级，由直观到抽象，由列举推演到逻辑推理，可谓一步步将学生引入“鸡兔同笼”问题的正解中。这个过程体现了循序渐进、螺旋式上升的教学结构，始终保持不变的主线就是“假设”的主体思路。

三、抽象概括，建立模型

在数学学习中，抽象概括能力是核心素养之一，是形成方法和制订步骤的重要保障，也是数学建模的基础。抽象是从许多同类事物中提取共性，过滤掉非本质因素，并加以认识的思维活动。在数学中，抽象表现为抽取数量关系，提炼出几何性质。当学生在头脑中形成基本的数量关系后，教师还需加强引导，帮助学生厘清数量关系。在学生能初步用假设法解答“鸡兔同笼”问题后，教师要注意引导学生关注“鸡兔同笼”这类问题的基本特征，以及描摹出数量关系的框架。首先是已知两个未知量的和，以及两个未知量的不同倍数和，分别求两个未知量;其次是揭示解题方法以及原理依据，即假设法的设计思路;最后是带领学生深度思索：“哪些问题可以划归为‘鸡兔同笼问题？”93EE35CE-D1BE-4090-A9D4-1C955D4E12EE

在学生普遍感到困惑时，教师可以带领学生继续研究类似的“鳄鸭同游”和“鸡猪同行”问题，并发问：“‘鸡兔同笼问题有什么独特之处？‘鸡兔同笼问题只能是鸡兔吗？”经过前后对比分析，学生就能发现：“红腹锦鸡和荷兰侏儒兔同笼”问题不只是红腹锦鸡、荷兰侏儒兔同笼的问题，换成其他品种的鸡和兔子也行，甚至换成其他动物也行，只要两种动物一种是两肢，另一种是四肢即可，如鸡猪问题、牛鸭问题。甚至继续抽象，只要两种同属事物的相同部位存在2和4的配比，都可认定为“鸡兔同笼”问题，如汽车和自行车的轮子问题。

随后，继续抽象，剥离同种事物的束缚，只抽象出数据，甚至2和4的配比都可以更改，如“存钱罐里储存着5元和2元两种面值的钞票，数一数一共有8张，合计34元，存钱罐里面值5元和面值2元的钞票各有多少张？”的题目，探讨其与“鸡兔同笼”问题的相关性。

经过比较和分析，学生的思维再次得到提高，有学生说：“这里面值2元的钞票就相当于红腹锦鸡，而5元的钞票就相当于荷兰侏儒兔，只不过这只‘兔子长了5条腿。”

最后，教师让学生广泛联系生活，将熟悉的事物编写成“鸡兔同笼”问题，而且是“变异红腹锦鸡与变异荷兰侏儒兔同笼”的数学问题，也就是彻底解除2和4的配比限制。

课堂总结时，教师向学生提出问题：“通过对‘鸡兔同笼问题的研究，你获得了哪些启示？”概括地说，即从某一个问题出发，先研究解法，然后推广到所有类似问题，建立基础模型，最后不断抽离情境条件，逐渐提炼出数学问题。

回顾上述教学，在对“鸡兔同笼”问题的深度思考过程中，尽管每次思考的问题和方法不同，究其本质都是逐渐帮助学生建模的过程。第一层次着眼于单一的“鸡兔同笼”问题，主要是激发学生的解题动机;第二层次则指向“鸡兔同笼”这一类问题的基本结构和解题策略，形成一种初步的数学化思维;第三层次是抽象化的“理论模型”建构，剥离一切外在情境和非本质因素的束缚，建立完全抽象化的数学理论模型，其涵盖面更广。

四、拓展延伸，助力建模

帮助学生较为理想地建构起基本的数学思维模型，以及问题解决的思维模型，是一个极其复杂的教学过程，也是一个跨时较长的艰难历程。故而，在“鸡兔同笼”问题的教学中，教师不仅要做到上述三个层次，更要跳出这三个层次。尽管这个时候学生已经较为系统地抽象出数学模型，获得了一定的解决“鸡兔同笼”问题的经验，但是教师还得尝试把这一问题进行拓展、延伸，以扩充学生的学习容量，给予他们更多的学习体验。

1.介绍同类问题的不同现象

首先，利用现代多媒体技术展示一则数学故事，并引导学生进行阅读。在阅读中学生发现，中国古老的“鸡兔同笼”问题也会漂洋过海，摇身变为《算法童子问》中的“狗与章鱼的故事”。进而引导学生思考：“这是数学问题吗？如果是，那么与‘鸡兔同笼问题是一样的吗？”

其次，引导学生探究这个问题，尝试用已经掌握的数学思维模型去提炼和研究。学生将故事提炼为“一群狗与一堆章鱼在玩耍，远远望去，有着15个头，看看地上，有着88条腿。这里的章鱼和狗各有多少只？”，学生开动脑筋，运用前面积累的经验和形成的解题模型去研究问题。有的采取画图策略，画出15个圆圈代表头数，在每个圆圈下画上4条竖线，代表4条腿。假设全是狗，通过计算发现多出88-4×15=28（条）腿。为什么会多出腿呢？因为章鱼有8条腿，这样学生就会在部分图案上再补上4条腿，也就得出章鱼的只数和狗的只数了。

最后，教师还可以向学生介绍“龟鹤”问题，引导学生进行有效的学习迁移，让他们去审视该问题与前面的“狗与章鱼的故事”“鸡兔同笼”问题的本质联系，从而让学生在趣味化的学习中更好地解决数学问题。

2.研究变式问题的基本规律

除了让学生将问题进行迁移，教师还得再度拓展问题，以激发学生个性化学习的动力，让“鸡兔同笼”问题的模型建立得更扎实、更牢靠。

比如，设计出这样一类问题：赵小亮参加科学知识竞赛，一共50道问题，抢答对1题可以得到2分，答错则要倒扣1分。比赛结束后，赵小亮得到85分。赵小亮答错了多少题？在这里需要学生更进一步地阅读与思考，让他们深入理解“答错则要倒扣1分”的本质。经过自主思考和同伴互动学习，学生在思维交锋中悟出：倒扣1分，就是在获得的分数中减去1分，本质就是每答错1题，失去的分数是1+2=3（分），问题的核心堡垒被攻克，解决它就水到渠成了。

综上所述，数学学习要让学生经历数学建模的完整过程，掌握数学建模的整套科学流程。当学生学会建模之后，他们对待问题的站位会更高，眼光会更开阔，能窥一斑而知全豹。当然，这个过程不是一蹴而就的，需要长期积累。

[ 参 考 文 献 ]

[1] 徐晓良.“笨”方法也是“好”方法：《鸡兔同笼》单元重组引发的思考[J].小学教学设计，2020（32）：39-41.

[2] 罗增儒.基于综合实践活动的教学探究：“鸡兔同笼”听课札记[J].中小学课堂教学研究，2020（09）：42-44，49.

[3] 贲友林.课堂学习，让每位学生都“+1”：《“鸡兔同笼”问题》教学与思考[J].教育视界，2020（23）：21-28.

[4] 陈彩琴.深究鸡兔同笼中蕴含的数学思想，助力思维发展[J].数学教学通讯，2020（01）：45-46.

[5] 刘顺平.在假设与转换中解决“鸡兔同笼”问题[J].中小學数学：小学版，2021（09）：22-23.

（责编 覃小慧）93EE35CE-D1BE-4090-A9D4-1C955D4E12EE