解读教材，为实现儿童数学思维层面的进阶助力

【摘要】文章以苏教版小学数学教材为例，通过分析教材中“认识正比例”一课编排的内容，思考该教材在培养学生数学能力方面的意图，并进行了相关的教学实践，从教学实践中反思不足与应对策略，以期提高小学数学教师解读教材、运用教材的能力。

【关键词】正比例;小学数学;解读教材

作者简介：祝猛（1981—），女，江苏省仪征市仪化第一小学。

多年执教毕业班的经历让笔者越发感受到苏教版教材编者们的殚精竭虑，他们将知识点纵横排布，使知识点的发展呈现出螺旋上升的效果。同时，笔者也深刻意识到“草蛇灰线，伏延千里”的说法不只是对文学作品撰写技法的评价，也可以用来评价小学数学教材的编纂。教师作为教材的使用者、实施者，需要做一个有心人，努力深入理解教材，从而为实现儿童数学思维层面的进阶助力。本文以苏教版数学六年级下册第六单元第1课时的研究分析及实践为例，探讨小学数学教师如何从儿童出发理解教材、解读教材，为实现儿童数学思维层面的进阶助力。

一、教材分析

（一）苏教版教材分析

江苏教育出版社出版的小学数学教材即苏教版教材六年级下册在第六单元第1课时安排了“认识正比例”的内容，这部分内容是在学生已学习了比（苏教版教材六年级上册）和比例（苏教版教材六年级下册）的知识的基础上安排的。主要目的是让学生结合实际情境认识正比例的量。

笔者在实际教学时，发现对于这部分知识，学生学习兴趣不浓。究其原因，是这部分内容逻辑性强，学生学习起来感觉很抽象，不容易与自己的生活建立联系，无法结合自己的经验去理解。同时，判断两个量是否成正比例关系需要规范表达，通常教师会要求学生提供完整的“比的式子、数量关系式、判断结论”“三部曲”，这也让一些学生产生畏难情绪。因此，教师如果仅仅从教材提供的表格数据入手，会导致学生的学习稍显枯燥和被动。[1]

（二）其他版本教材的分析

笔者研究现行的小学数学教材，发现大多数版本教材都把这一部分内容编排在六年级下册，这是基于小学生的年龄及学习方式特点考虑的。人教版和苏教版异曲同工，其编排也是以小学数学的几大核心数量关系为基础，结合表格数据关系及变化来呈现。北师大版在编排正比例之前，先安排了“变化的量”一节，引导学生结合统计表和折线统计图，对什么是“相关联的量”进行概念建立，紧紧扣住“一个量变化引起另一个量变化”的核心，为后面的教学做铺垫。浙教版则让人眼前一亮，将正比例的图像与相关联的量的数据相结合，不同于上面提到的几个版本教材只是提到“一个量变化，另一个量也随之变化”这点，浙教版教材中引导学生进行了更为准确的描述—“时间是原来的几倍，路程也是原来的几倍，时间是原来的几分之一，路程也是原来的几分之一。”这样能够让学生结合已有的数学经验（两个量的倍数关系、分数关系）更形象地用数学语言准确描述比例的变化关系，从而促进自身数学思维的深层次发展[2]。

二、教材思考

通过对以上几个版本教材的分析与思考，笔者认为，孩子进行数学学习的起点是他们积累的生活常识和经验，小学阶段学生的数学学习思维具有明显的直观化特征。发现学习和深度学习的观点也告诉我们，要尝试引导学生在学习中充分调取前经验，尝试对新知进行初步建构。通过向学生提供一定的背景材料或情境，由学生独立操作、创造，让他们在对话、辨析过程中，不断经历观念打破、知识重构的过程，实现新旧知识之间的关联，完成对知识本质认识的不断进阶。

笔者认为“认识正比例”的教学设计应充分考虑儿童的心理特点、学习方式特点，从学生已有知识经验出发，进行如下实践。

三、教学实践

实践操作一：从研究一组数量的变化特征入手

1.教师出示一本笔记本。

师：假如这本笔记本的單价是1元，你还能知道什么？

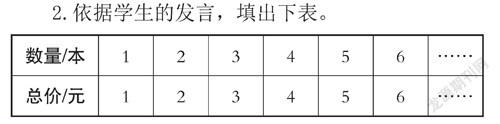
2.依据学生的发言，填出下表。

3.引导观察，同桌交流。

师： 想一想购买笔记本的总钱数与本数之间有怎样的关系？

生：总钱数随着笔记本数量的增加而增加。

师（追问）：在这个表格中总价和数量在不断地变化，什么又是不变的呢？

生：笔记本的单价不变。

4.归纳概括。教师根据学生的回答，板书（或PPT出示）相对应数量的比“1∶1=1 2∶2=1 3∶3=1 4∶4=1……”，在列举的过程中强调比值不变，在此基础上概括出总价和数量成正比例关系。

分析：教师从学生常见的笔记本的总价、数量入手，调动学生的生活经验，能在课堂上较快地揭示并概括出正比例概念。

思考：仅仅是基于这一组数据的特殊性，学生是否能真正地如教师所料的那样顺利地得出“比的变化关系”，真正理解比例的知识，这有待我们教师进一步思考。

实践操作二：从研究多组数量的共同规律入手

1.教师出示两张表格，如右上所示。

2.引发学生思考，在理解的基础上进行抽象概括。

师：请同学们认真观察这两个表格中的数量，思考这些数量的变化有没有什么共同点？

相信六年级下学期的学生通过独立观察，大多数都会发现每个表格中每两个相关联的数量都有一个量随着另一个量的变化而变化。教师会很顺利地引出教学任务—认识正比例。

思考：教师采用这样的导入，学生发现数量规律一定比“实践操作一”要慢得多。但教师通过设计多组数量，让学生充分观察，促使学生自主地利用类比的思想去发现不同组别数量中每组数量变化的共性，能够更有效地促进学生思维的发展，培养学生较深层次的数学思维[3]。

实践操作三：从研究多组数量的不同变化入手

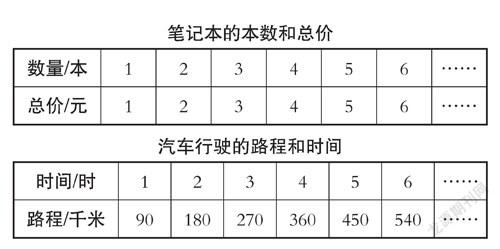
1.教师出示如下3张表格。

师：请同学们将3组表格的数据填写完整。

过程：学生们在独立填写表格时会意识到，第一个表格时间与路程、第二个表格本数与总价之间的变化是有规律的，而最后一个表格中红红的年龄与身高两个数量的变化并没有规律。在对比中，学生逐渐认识到时间与路程、本数与总价两个数量变化的共同规律，从而在理解的基础上概括出正比例概念。

思考：“实践操作三”与“实践操作二”相比，其导入增设了一组有不同变化规律的数量的表格。学生通过比较异同点，能更好地把握比例知识本质，分清知识间的联系与区别，从而达到对知识本质和规律的理性认识。

实践操作四：动态呈现，任务驱动

教师首先为学生依次呈现两张动态的折线统计图（图略），并给出学习任务，要求学生独立思考，分析数据，辨析异同。

用学生已经学过的折线统计图开展教学，为学生提供了观察、思考的空间，为他们发现问题、提出问题、分析问题、解决问题创设了情境。在任务驱动的基础上，让学生充分进行独立思考和小组合作。

生1：从两张折线统计图中可看出路程和时间两种数量关系式，即路程÷时间=速度。

生2：7小时行驶的路程相同。

生3：平均速度都是每小时80千米。

生4：一个是直线，一个是曲线。

生5：第一个折线图直线速度没变，第二个折线图速度变了。

……

因为有了对比过程中的直观感受，学生们自然抓住了“路程÷时间=速度”“速度变与不变”以及“直线”这三处核心。“正比例关系中两个相关联的量的变化方向相同，反比例关系中两个相关联的量的变化方向相反”，这里面的“正”与“反”需要在比较的过程中才能充分理解。

四、反思与策略

在进行教材分析与教学实践后，在笔者与同行的讨论中，同行针对苏教版教材与本节课教学实践提出了一些不足之处。

1.认为教材编排有不足：没有对什么是“两个相关联的量”进行更集中的解读与辨析。

针对这点，笔者提出其实苏教版教材在其他的例题中强调了“两个相关联的量”，比如苏教版教材第十册中的折线统计图就有所体现。此外，苏教版教材第十二册第四单元中的比例部分的内容也多次引导学生结合表格及数据进行分析比较两個数量的关系。当然，这就需要教师充分理解教材，关注知识点的排布，才能够真正在日常教学中将知识串点成线。比如在五年级折线统计图的教学中，教师不仅要让学生会看折线统计图，从中收集信息、分析信息，也要让他们初步感受折线图的动态变化过程;而在六年级下册比例知识的教学中，教师不仅要让学生对表格中相对应的两个数量是否有比例关系进行分析，也要让学生体会到“两个对应的量，一个变化，另一个也随之变化”的规律。从笔者在多个毕业班的教学实践来看，小学阶段的学生是具备相关认知能力的。但要达到这些教学目标也对教师提出了较高的要求，教师需要对教材有深入的研究思考[4]。

2.认为教学实践有不足：没有在本节课中对“两个量之间存在的不同关联”进行梳理与架构。

小学数学中研究的两个量可能是有关联的，比如商一定（通常是正比例关系）、积一定（通常是反比例关系），也有和一定、差一定，当然也有的两个量没有直接关联，比如身高与年龄、体重与年龄的关系等。教师架构两个量之间存在的不同关联的知识，有利于学生建立知识结构，为中学函数知识的学习打下基础。小学的正比例、反比例学习不仅为孩子们初中的函数研究打开了一扇门，也为孩子们建立了现实具体世界与数学抽象世界的桥梁。而上述教学实践中确实忽视了知识的架构。

笔者认为，教材为学生呈现的只是静态内容，而教师可以做的便是在深度理解及研究教材的基础上，为孩子们呈现知识建立、变化的动态过程，引发他们深层次的数学思考，用数学视野看待数学知识，看待世界中存在的数学现象。

从儿童出发，让儿童的数学基本思想方法和活动经验得到进阶，为他们的思维发展提供支持，将是小学数学教师的不懈追求。

【参考文献】

[1]在实践中创新，在创新中立意—成都市杨薪意名师工作室简介[J].小学教学（数学版），2021（02）：74.

[2]高爱萍.做思用合一：行知思想在小学数学教学中的实践[J].小学教学参考，2020（35）：55-56.

[3]张兰.贯彻“行知思想”优化数学教学[J].教学管理与教育研究，2019（20）：83-84.

[4]岳川.小学数学教学提升学生学习力的策略分析[J].数学学习与研究，2020（11）：160-161.