从问题中挖掘内涵 渗透类比思想

李欢 祝丽萍

【摘要】本文试着遵循波利亚“怎样解题表”的基本理念，让学生通过经历系列问题的解题思路探究过程，领悟蕴含在其中的“归纳”“类比”“一般化”“特殊化”“差异分析”等基本的数学思想方法，培育学生“透过现象，揭示本质”的数学抽象核心素养.

【关键词】类比思想;数学教学;抽象思维

1 问题的提出

沪教版《普通高中课程标准实验教科书》数学必修三第10章P9习题B组第1题是：

“1个平面把空间分成2部分，2个平面把空间分成3部分或4部分，3个平面把空间分成几部分？”由于学生对1维、2维及3维空间非常熟悉，所以很容易得出答案.但若将题目稍做改动，即“4个平面把空间分成几部分？”许多学生便对“4个平面最多把空间分成几部分”这一情况束手无措.其实这正是著名的几何学家斯坦纳提出的的经典问题“n个平面最多可将空间分割成多少部分？”的特殊情况.

鉴于“平面分割空间问题”在中学数学教学中并不是初次出现，而是有一系列类似问题，例如“点分割直线问题”“直线分割平面问题”等，但教材中没有系统的将类似问题整合，未给出研究系列问题的具体方法.

利用初等方法得出：

点最多能将直线分割的部分数：f1（n）=C0n+C1n，

直线最多能将平面分割的部分数：f2（n）=C0n+C1n+C2n，

平面最多能将空间分割的部分数：f3（n）=C0n+C1n+C2n+C3n.

最后猜想将结论推广至任意正整数维空间.

2 实践波利亚“怎样解题表”的探究式解题教学实录

2.1 直线分割平面问题

师 我们对n个点最多能将一条直线分为（n+1）个部分这个结论比较清楚，那么，上述问题是否可以进行推广呢？

生1 可以！

问题1 n条直线最多能将一个平面分成多少部分呢？

师 “类比是发现问题的开拓者”，同学们提出了一个很好的问题，但是n条直线满足什么条件才能将一个平面分成的部分最多呢？

生2 ①任意两条直线相交;②没有两条以上的直线通过同一点.

师 很好！为了方便叙述问题，记平面被直线最多分成的部分数为f2（n），如何计算f2（n）？

生3 可以先将问题特殊化，通过画图可直观得出当n=1，2，3…时，f2（1）=2，f2（2）=4，f2（3）=7…

师 非常棒！但我们对3条直线分割平面问题比较陌生，所以分析一下“7”是怎么得出的？

生茫然……

师 3条直线相交最复杂的情况便是交成一个三角形（图1），可以从有限部分与无限部分进行观察？

图1

生4 有限部分有1个，就是三角形的内部（①）;无限部分中与三角形有公共顶点有3个部分（②③④）;与三角形有公共边有3个部分（⑤⑥⑦）.把这些分割部分的数目加起来，即1+3+3=7，7个部分就是这样来的.

师 你能否仿照上述分析，回答4条直线最多可将一个平面分成几部分？

生5 1（1个四边形）+4（4个公共边）+6（6个公共顶点）=11.

师 为你点赞！通过类似地分析，相信同学们也能解决5条、6条等更多直线分割平面最多的部分数.但随着直线条数增多，画图难度就会加大.因此，你是否可以找到一般化的规律？即你能否一眼看出问题1的答案？

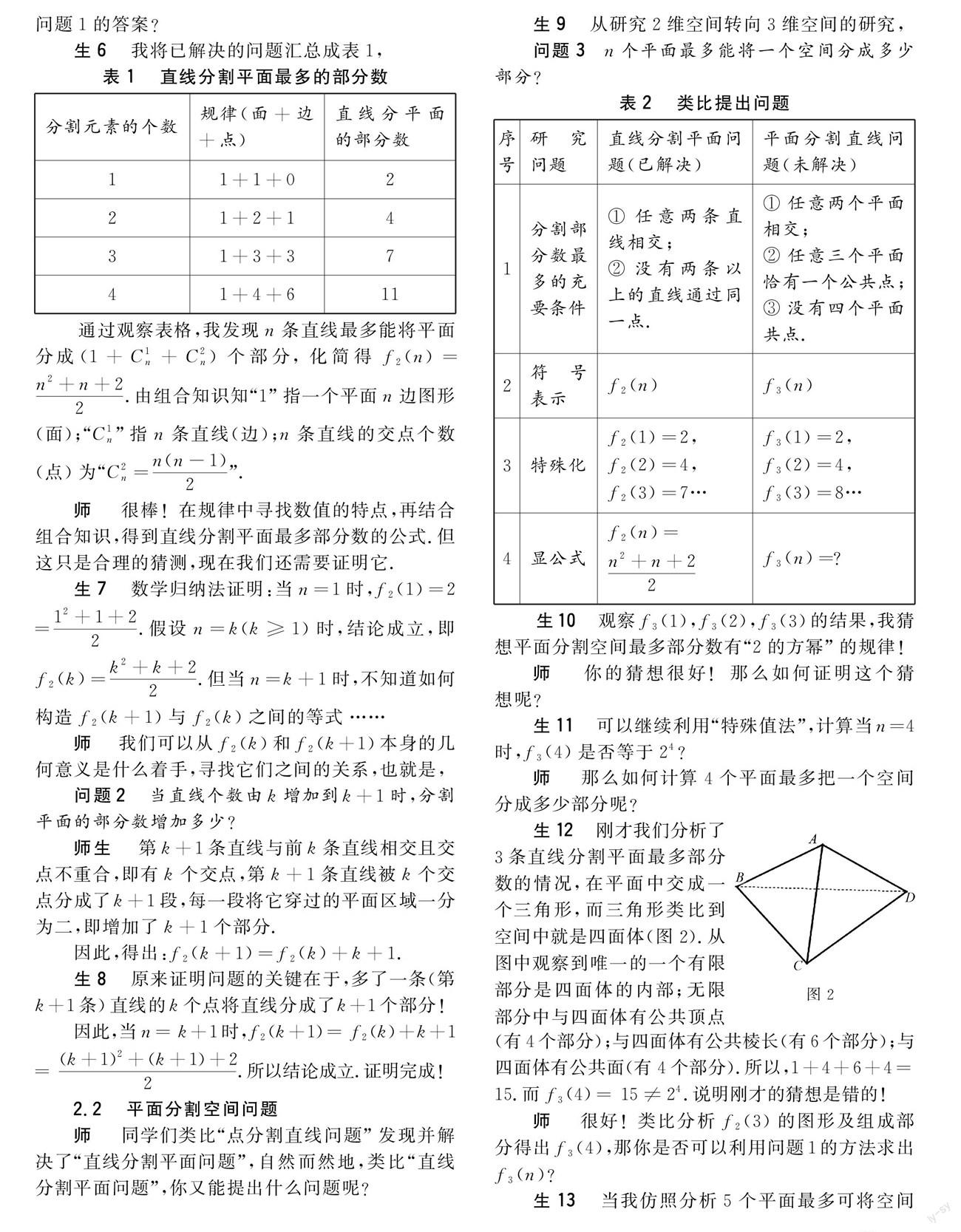
生6 我将已解决的问题汇总成表1，

通过观察表格，我发现n条直线最多能将平面分成（1+C1n+C2n）个部分，化简得f2（n）=n2+n+22.由组合知识知“1”指一个平面n边图形（面）;“C1n”指n条直线（边）;n条直线的交点个数（点）为“C2n=n（n-1）2”.

师 很棒！在规律中寻找数值的特点，再结合组合知识，得到直线分割平面最多部分数的公式.但这只是合理的猜测，现在我们还需要证明它.

生7 数学归纳法证明：当n=1时，f2（1）=2=12+1+22.假设n=k（k≥1）时，结论成立，即f2（k）=k2+k+22.但当n=k+1时，不知道如何构造f2（k+1）与f2（k）之间的等式……

师 我们可以从f2（k）和f2（k+1）本身的几何意义是什么着手，寻找它们之间的关系，也就是，

问题2 当直线个数由k增加到k+1时，分割平面的部分数增加多少？

师生 第k+1条直线与前k条直线相交且交点不重合，即有k个交点，第k+1条直线被k个交点分成了k+1段，每一段将它穿过的平面区域一分为二，即增加了k+1个部分.

因此，得出：f2（k+1）=f2（k）+k+1.

生8 原来证明问题的关键在于，多了一条（第k+1条）直线的k个点将直线分成了k+1个部分！

因此，当n=k+1时，f2（k+1）=f2（k）+k+1=（k+1）2+（k+1）+22.所以结论成立.证明完成！

2.2 平面分割空间问题

师 同学们类比“点分割直线问题”发现并解决了“直线分割平面问题”，自然而然地，类比“直线分割平面问题”，你又能提出什么问题呢？

生9 从研究2维空间转向3维空间的研究，

问题3 n个平面最多能将一个空间分成多少部分？

生10 观察f3（1），f3（2），f3（3）的结果，我猜想平面分割空间最多部分数有“2的方幂”的规律！

师 你的猜想很好！那么如何证明这个猜想呢？

生11 可以继续利用“特殊值法”，计算当n=4时，f3（4）是否等于24？

师 那么如何计算4个平面最多把一个空间分成多少部分呢？

生12 刚才我们分析了3条直线分割平面最多部分数的情况，在平面中交成一个三角形，而三角形类比到空间中就是四面体（图2）.从图中观察到唯一的一个有限部分是四面体的内部;无限部分中与四面体有公共顶点（有4個部分）;与四面体有公共棱长（有6个部分）;与四面体有公共面（有4个部分）.所以，1+4+6+4=15.而f3（4）=15≠24.说明刚才的猜想是错的！

师 很好！类比分析f2（3）的图形及组成部分得出f3（4），那你是否可以利用问题1的方法求出f3（n）？

生13 当我仿照分析5个平面最多可将空间分割成多少部分时，我发现这一问题在平面上的类比图形是什么？是5条直线还是4条直线分割平面？又如何类比？不容易想清楚了.说明不能利用问题1方法归纳猜想公式.

师 非常棒，那我们只能源于以前的经验和知识另辟新径！由于孤立的问题有时候难以解决，解决系列问题有时要比解决孤立问题更好入手.因此，现在我们把极端情况（有零个分割元素的情况）也考虑在内，那么被“分割”成的部分数都是1;零个点最多把直线分成1个部分;零条直线最多把平面分成1个部分;零个平面最多把空间分成1个部分.记直线被点最多分成的部分数为f1（n）.

师 整体观察上表（表3）中已解决的问题，看看表中的数字间有什么联系？

生14 我发现表格中呈“阶梯型数值”有规律，例如（表4）联想到3+4=7，7+8=15.

师 这是一个独特的联系.也就是说表中已出现的每个数都可以由它“头上”的数与“左肩”上的数相加而得到.可为什么会有这么神奇的规律呢，能否用几何意义分析？比如这里的“8”代表什么？“7”又有何意义？

生15 “8”指3个平面分空间最多为8个部分;

师生 “7”指在再添加一个平面（第4个平面），第4个平面与原来的3个平面都相交，并且又不过原来3个平面的交点，从而不过原来任两平面的交线，这就交出了3条新直线，这3条新直线把新添加的平面分为7个部分（就是表3中的“7”），每一部分把它穿过的（由前3个平面分成的）区域一分为二，因此“空间分割”增加了7个部分，而原有8个部分，这就是15=7+8的逻辑推理过程.

生16 通过类比、归纳还可以得到递推公式：

f2（n）=f2（n-1）+f1（n-1）.  （1）

f3（n）=f3（n-1）+f2（n-1）.  （2）

师 你观察得可真仔细，为你点赞！但这只是合情合理的猜想，我们仍需像推理“15=7+8”的来源一样严格分析递推公式，以此肯定或否定它.但刚才我们已经证明了平面分割空间最多部分数的特殊情况，即n=3到n=4的过渡，你能完全类似分析由n-1到n的过渡发生的情况吗？

生17 “f3（n-1）”指n-1个平面分空间最多为f3（n-1）个部分;“f2（n-1）”指再添加一个平面（第n个平面），第n个平面与原来的n-1个平面都相交，并且又不过原来任3个平面的交点，从而不过原来任两平面的交线.这就交出了n-1条新直线，这n-1条新直线把新添的平面分为f2（n-1）个部分，每一部分把它穿过的（由前n-1个平面分成的）区域一分为二，因此“空间分割”增加了f2（n-1）个部分，而原有f3（n-1）个部分，所以现在空间共被分割成的“部分数”是f3（n）=f3（n-1）+f2（n-1）.

师 我们已严格证明递推公式（2），你能利用递推公式的相关知识推出它的显公式吗？

生18 移项得：f3（n）-f3（n-1）=f2（n-1）.递推，得f3（n）=f3（1）+f2（1）+f2（2）+…+f2（n-1）

=2+12∑n-1i=1i2+∑n-1i=1i+（n-1）=16（n3+5n+6）.

生19 咦！那也可以先利用递推公式猜测得出显公式，再像问题1一样用数学归纳法证明它.并且将问题2类比可以得到问题4，

问题4 当平面个数由k增加至k+1时，分割平面的部分数增加多少？

第k+1个平面与前k个平面都相交但不过任2个平面的交线，即有k个交线，第k+1个平面被k个交线分成了f2（k）个部分，每一部分把它穿过的空间区域一分为二，即增加了f2（k）个部分.

因此，得出：f3（k+1）=f3（k）+f2（k）.  （数学归纳法其余步骤此处省略）

该等式意味着，多了一个（第k+1个）平面的k条直线将平面分成了f2（k）个部分.

师 你说的完全正确！类似地你可以仿照递推公式（2）的几何思考过程并重新证明问题1.

（学生模仿生16证明过程，限于篇幅，此处省略.）

2.3 平面分割空间问题的推广

师 尽管我们中学阶段只学习了3维空间及以下空间，但同学们是否可以大胆尝试一下，猜想4维空间被分割的显公式，

问题5 n个三维空间最多可将一个四维空间分成多少部分？

生20 递推公式：f4（n）=f4（n-1）+f3（n-1）.由于我们已经掌握f3（n-1）的计算公式，所以利用“累加法”猜测出问题4的显公式为：

124（n4-2n3+11n2+14n+24）.

师 如果推广至任意正整数维空间呢？

问题6 n个k-1维空间最多可将一个k维空间分成多少部分？

生21 递推公式：fk（n）=fk（n-1）+fk-1（n-1）.至于推出“fk（n）”的显公式需要知道“fk-1（n-1）”而“fk-1（n-1）”又要知道“fk-2（n-2）”，也就是说计算“下式”总要用到“上式”，但“上式”是什么，我就想不出来了.

生22 “3维空间分割4维空间问题”需化归为“平面分割空间问题”才能解决，而“平面分割空间问题”需化归为“直线分割平面问题”才能解决，但“直线分割平面问题”又与“点分割直线问题”息息相关，所以不管是哪类问题，最终都要化归为“点分割直线问题.”而以前我们就已经知道“点分割直线问题”就是要找与直线交点.

师 很棒！换言之就是区域的变化数与交点的变换有关系！重新从几何意义分析已解决的问题，任意一条直线上增加了n个点，交点增加了n个，直线上的区域数就增加了n个部分，几何元素由任意一条直线（C0n）变成了“直线+点”（C0n+C1n）;任意一个平面上增加了n條不平行且三条之间不过同一点直线，交点增加了C2n个，平面的区域数也就增加了C2n个部分，几何元素由任意一个平面（C1n）变成了“平面+直线+点”（C0n+C1n+C2n），……这不是偶然，这正是分割部分数公式的本质原因！

（证明需要大学拓扑学欧拉-庞加莱公式和数学归纳法，限于学生已有知识，不再赘述）

类似地，你能重新改写问题（见表5）的显公式吗？

生23 可以！

师 基于上述规律，你能猜想出任意正整数k维空间被分割的公式吗？

生24 fk（n）=C0n+C1n+…+Ck-1n+Ckn.

师 这其实是大学数学拓扑学中的知识，

定理：一个k维欧氏空间Rk最多可以被n个k-1维欧氏空间Rk分割成的区域数为fk（n）=∑ki=0Cin.

师 至此我们完成了分空间最多部分数的探索，发现并证明研究分空间最多部分数工具—递推公式和数学归纳法，它的显公式与组合数有关，当我们越发现系列问题的本质时问题变得就越简单.

参考文献：

[1]波利亚著;涂泓，冯承天译.怎样解题——数学思维的新方法[M].上海：上海科技教育出版社，2011.

[2]季苹，《从“备学生”转向“研究学生”—基于学生研究的数学教学》，[M]，教育科学出版社，2015.7.