微元法在高中物理解题中的应用

高永生

【摘要】在高中物理解题中使用微元法，可以通过宏观分割的方式将物理变量分割成若干个“元过程”，从而有效简化分析过程，构建起理想模型，极有助于顺利攻克习题.本文主要结合运动学、“功”和“能”、动量、电磁学方面的例题，围绕微元法的具体运用一一做了阐释.

【关键词】微元法;高中物理;运动学

新课程改革背景下，高中物理课程标准针对学生“科学思维”这一核心素养发展提出了更高要求.微元法是物理学科中常用的方法，也是高中生解答物理题目的重要工具，其采用宏观分割的方式，根据需要将物理变量分割成若干个“元过程”以简化分析过程，从而构建起理想模型，最终顺利完成问题解答.合理利用微元法不仅能够提升学生的物理解题能力，而且有助于改善其物理思维.

基于此，本文结合多年高中物理教学经历与经验，对微元法的应用进行归纳总结，以期为今后的教学和教研提供一定的启示.

1 在“运动学”的解题中应用微元法

人教版高中物理教材开篇就是运动学的相关知识.在匀变速直线运动研究中，教材通过图示的方法说明v-t的图像中阴影部分面积等于总位移，鉴于部分学生对此存在理解偏差且在解题中出现错误，教师可以充分利用微元法，引导学生的解题思路，从而深化其对于运动学知识的理解和掌握^[1].

例1 某物体正在做加速直线运动，已知该物体初速度为v₀，加速度为a，经过时间t，请尝试推导物体的位移x与时间t的关系式为x=v₀t+at².

解析 根据微元法，可以把物体的运动过程分解成若干个细小的“微元”，在平面直角坐标系中能够看出，这些“微元”以t为高，以在纵轴上所取的长度为上下底的梯形，当t不断缩小，所构成的梯形则无限趋近于长方形（如图1），而其中阴影的面积则可以表示为总位移.经过微元的过程，位移x与时间t的模型得到了优化，也可以直观看出，阴影部分的面积能够通过长方形和三角形相加获得，故根据图形所示，阴影的面积为x=v₀t+at².

这是一道比較简单和典型的位移问题，微元法的运用既能更有规律地呈现出速度与时间的变化，又能让模型变得更为理想，故而学生在计算过程中能够通过数形结合的方式直观了解位移的几何含义，进而完成推导论证.

2 在“功”和“能”的解题中应用微元法

能量守恒定律是高中生需要掌握的重要理论，相关题目中经常见到的变力做功问题，极易让很多学生一头雾水，找不到解题思路.围绕做功和能量的转化进行分析，教师可以引入微元法，启发学生结合函数等方面的知识，找到解题思路，形成理性作答^[2].

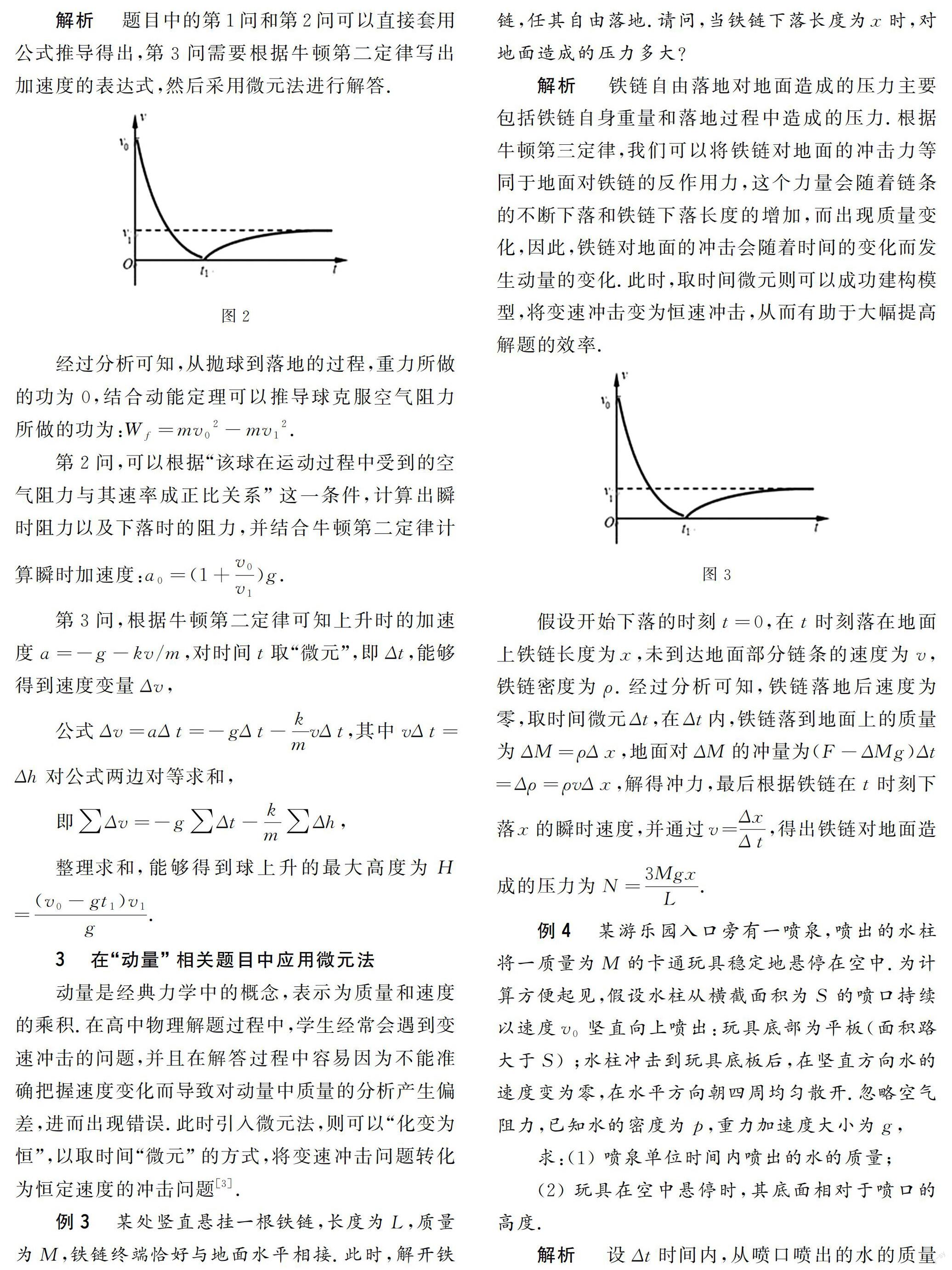
例2 甲以v₀的初速度将一质量为m的球竖直向上抛出，假设该球在运动过程中受到的空气阻力与其速率成正比关系，并且其速率随时间的变化规律如图2所示.那么，当球向上运动在t₁到达最高点，然后匀速下落，落地时速率为v₁.

请计算（1）该球从抛出到落地过程中克服空气阻力所做的功;

（2）球抛出瞬间的加速度;

（3）球上升的最大高度.