重视探究过程，升华基本作图

阙成

【摘要】尺规作图作为初中数学几何教学中的一个基本内容，对学生培养空间想象、数学推理以及探究应用能力起到了重要的作用.在考试中，也出现过不少基于基本作图方法的题型.但在实际教学中，笔者发现学生对于基本作图的原理和作法掌握比较牢固.但对于需要分析题意，将"尺、规"作为工具达到问题解决的探究型问题比较茫然，无从下手.以下针对这一问题进行教学反思.

【关键词】尺规作图;基本作图;探究应用题呈现

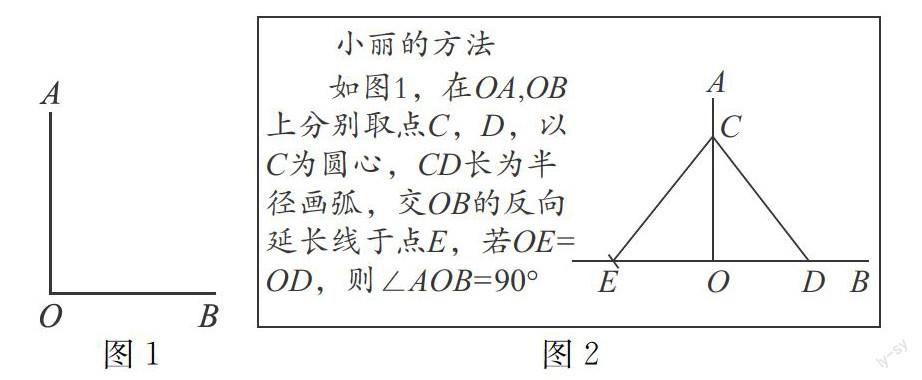
"直角"在初中几何学习中无处不在.如图1，已知∠AOB，请仿照小丽的方式，再用两种不同的方法判断∠AOB是否为直角（仅限用直尺和圆规）.

本题的作图不再是机械的作法，而是考察了作法背后灵活的思维以及知识迁移能力.最后，再通过尺规作图的基本作图方法规划作图步骤.所以，作图前的分析过程虽未呈现在答案中，但价值却在作法之上.

解析

方法1想到勾股定理逆定理中通过三角形三边之间的数量关系判定直角三角形的方法.若以点O 为端点在射线OA、OB上任取C、D两点，OC、OD、CD 满足OC2+OD2=CD2，则可说明∠AOB为直角.为了实现这一目的，我们可以先假设直角成立，为方便起见选取一组勾股数作为直角三角形边长，如3、4、5.由于圆规可用来截取相等的线段，我们只需要利用圆规作出表示3份和4份的两条直角边 OC、OD，再利用直尺连接CD，利用圆规验证 CD长度是否为对应的5份，

以此来判定∠AOB是直角.

方法2 想到圆中直径对直角，只要在射线 OA、OB上任取两点C、D以C、D为直径作圆，若点O 在圆上，则∠AOB=90°。

在这道题的解决过程中，很多同学无从下手.在与学生的交流中发现学生遇到了以下几点困惑：

1.学生在平时的练习中，更多接触到的是尺规基本作图，以及给出作法后的理由阐述问题.对于这一道题没有做好心态和方法上的准备;

2.学生在阅读材料后，难以联想到其他思路，也没有找到分析的方法;

3.即便是想到了利用勾股定理逆定理可以用来判定直角，但依舊无法利用尺规来实现.

针对这几个问题，我也开始反思教学中存在的一些不足.

2教学回顾

在实际教学中，以苏科版数学教材为例，五种尺规基本作图以.阅读作法，根据作法中的步骤操作"为主，在教学中，会有以下几点疏漏：

（1）学生很容易将其当做独立的学习内容，难以与其他知识点联系在一起.

（2）对于尺规作图的教学集中在具体的作法上，教师介绍作法，学生根据作法动手操作，但忽视了对作法原理的探究.使得作图与教材前后的内容相割裂.

（3）书本以及练习中配套的练习往往比较简单，是对基本作图的方法的不断重复.对于作图前的分析阶段锻炼不够.

同时，课标要求会利用基本作图作三角形与圆的相关图形，在实际教学中，也存在仅仅.就事论事"的情况，忽略了作图与三角形、圆中性质的联系.学生学完以后，基本上都还只局限在上课教过的图形作法上.把尺规作图当成是学习的目标，而不是解决实际问题的工具.

3教学改进尝试

根据这些教学中暴露出的问题，笔者也作出了几方面的教学尝试.

3.1深挖基本作图教学

以作一个角的平分线为例.学生在接触尺规作图之前，学生已经通过量角器、折纸、刻度尺、角尺等手段从几何直观和理性推理两方面得到了各种各样的作法，进而不难发现可以用"SSS，证明画法的正确性.这时，可以让学生体会到画角平分线的实质是构造两个用一条公共边的全等三角形.从而找到用"直尺和圆规，替换以上工具的来画角平分线的的办法.这程，实际上也是引导学生主动探索用直尺与圆规作角平分线的方法和原理.

3.2关注知识间的联系与交互

在一定量的按要求作图后，针对学生并没有真正应用尺规解决新问题，可以设计一些需要分析、整合已学内容的问题.如：

例题

本题以作四边形 ABCD为背景，考查了作平行线与做一条线段等于已知线段的两倍.其中作平行线的方法就是对学生推理能力，几何直观，转化思想的考验.可以请学生联系所学内容，分析探究.

法1直线的平行关系可通过构造同位角、内错角的相等关系转化.这就将问题转化为"作一个角等于已知角，的基本作图.

法2根据"垂直于同一条直线的两直线互相平行，构造平行线.具体来说，作 AB的垂线，再作过点C 且垂直于这条垂线的垂线.这样，就转化为"过一点作已知直线的垂线，的基本作图.其中，学生也提出"作 AB的垂线，作法不唯一，尝试、交流中发现可以过点C 作AB的垂线，或直接作 AB的中垂线.这又涉及到"作一条线段的垂直平分线，的基本作图.

法3根据"平分、等腰得平行，进行构造.作∠ABC的平分线，再以点 C为圆心，CB长为半径作弧，交角平分线于一点.连接点C与该点即为AB的平行线.这里，用到了"作一条线段等于已知线段，和"作一个角的平分线，两种基本作图.

以上三种作法，通过作图前的分析，寻找能够得出两直线平行的相关判定与方法，形成知识间的迁移.而且在学生探究的过程中，体验到了作图方法与几何推理间的密切联系.最终，学生发现还是通过五种基本作图来完成，但体会却更为深刻.

学生在进一步思考后还有很多非常好的想法.

法4以BA、BC为一组邻边构造平行四边形.利用平行四边形对边平行的性质得到平行线.

至此，学生体会到各个知识间丰富的交互与迁移，应用意识、创新思维达到真正的锻炼.

3.3深挖例题资源

回到文章一开始的问题，很多学生在做题过程中其实并没有仔细读题，"小丽的方法，实际上是一跳而过.在本题的评讲过程中，很多学生也只是记下了正确答案，之后就将本题弃之一边.那么这道题的价值就没有足够的体现，之后遇到探究型作图学生依旧一筹莫展.针对这一情况，课堂评讲可设置问题如下：

（1）小丽的方法原理是什么？

设问分析这实际上也是中考中常见的"给出作法，说原理，问题.对于学生来说，思维是正向的，切入难度低.学生可以从两三角形全等的角度阐述原理，也可以根据等腰三角形三线合一的相关知识分析.学生在试图说理的过程中，就是在进行知识间的迁移.

（2）解析给出的两种方法都是构造直角三角形，还有没有其他方式或模型可以迁移呢？

设问分析作图前的分析是解决本题，也是此类问题的关键所在.这个问题的设置，也是为了让学生明白，方法是多样的，是不唯一的.这是对学生灵活应用已有知识的考验，也是对创新精神的磨炼.

4结语

综上，从这一道题的分析与作图可以看出学生在尺规作图的学习中还存在很多的问题，基本作图只是一种工具，更需要学生灵活的思维，迁移知识的能力.而这，也是今后教学过程中需要注意的.我们不仅要培养学生具体操作的能力，更需要让学生学会分析，学会联想，真正发展学生的数学素养.

参考文献

[1]张万梅.一道中考尺规作图题画法赏析和思考[J].中小学数学（初中版）.2020（06）

[2]陆蓉.一道尺规作图题的阅卷收获[J].初中数学教与学.2020（03）

[3]孙喜军.一道中考尺规作图题的多解及探究[J].数学教学，2020（06）：19 -21.