如何理解分数的意义

何奶群

（五年级）

如何更好地理解分数的意义？可以采用以下教学过程。

一、画图表征，唤醒分数的原认知

教师提问：“[14]可以表示什么？用画图的方式举例说明。”学生独立思考，组内交流，教师巡视，寻找典型答案。

预设学生会有以下几类答案（如图1）。

二、讨论交流，直击分数本质

1.寻找相同点，理解分数的意义

先让学生分别说一说每幅图的意思，接着教师追问：“图③和图④分别涂了1个爱心和4个正方形，为什么不用1和4来表示，而要用[14]表示？”学生通过讨论发现，图③是把4个爱心看作一个整体，图④是把16个正方形看作一个整体。

在学生观察、比较图①～④后，教师提出问题：“这四幅图有什么相同點？”引导学生发现都是把一个物体、一个计量单位或一些物体看作一个整体，用单位“1”表示;都平均分成了4份，取了其中的1份，可以用[14]表示。

2.观察图式，体会分数的多元表征

教师引导学生观察图④并提问：“除了[14]，还可以用哪个分数表示？”学生独立思考，组内交流，发现还可以用[28]，[416]来表示。

教师继续提问：“用[416]表示，是怎么想的？”先引导学生完整表述：把16个正方形看作单位“1”，平均分成16份，其中的4份可以用[416]表示，再让同桌互相说一说[28]的意思。

三、变式练习，理解单位“1”的含义

1.理解“相同数量，却用不同分数表示”

教师出示题目：一袋糖有12颗。

（1）第一次拿出2颗，拿出了全部的[（   ）（    ）]。

（2）第二次再拿出2颗，拿出了剩余的[（   ）（    ）]。

让学生解答后进行对比思考：“同样是2颗糖，为什么一会儿用[212]表示，一会儿用[210]表示？”引导学生体会虽然都是2颗糖，但对应的单位“1”不同，所以表示的分数也不同。

2.理解“相同分数，却表示不同数量”

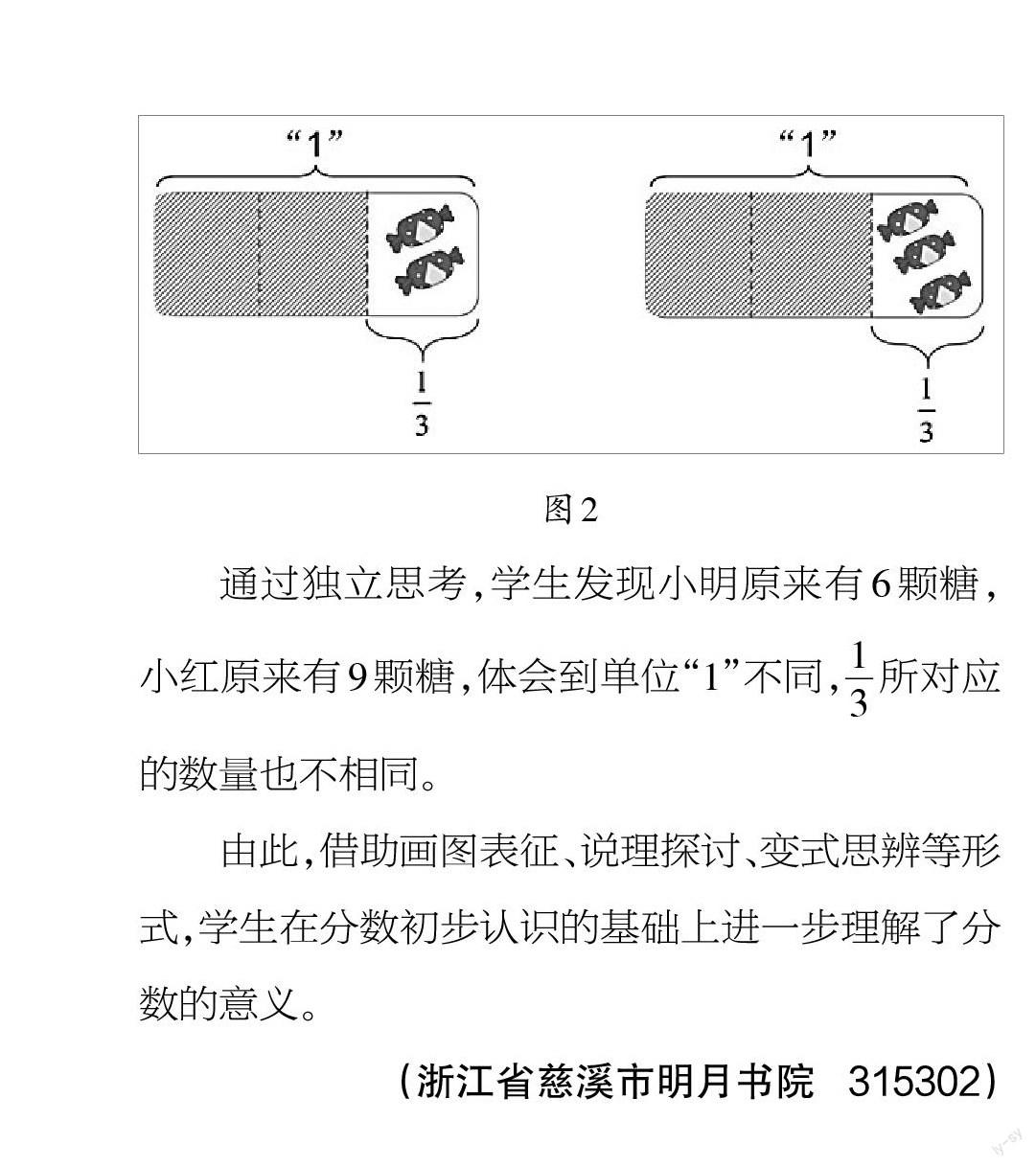
教师出示题目：小明和小红都取了各自糖果数量的[13]，小明取出了2颗，小红取出了3颗。他们原来分别有几颗糖？

让学生独立解题，并提示他们用图式表示题意（如图2）。

通过独立思考，学生发现小明原来有6颗糖，小红原来有9颗糖，体会到单位“1”不同，[13]所对应的数量也不相同。

由此，借助画图表征、说理探讨、变式思辨等形式，学生在分数初步认识的基础上进一步理解了分数的意义。

（浙江省慈溪市明月书院   315302）