基于“一题一课”的小学数学练习教学策略

平燕

【摘   要】基于“一题一课”开展练习教学，可以从学生错误之处、知识迁移之处、思维渗透之处精选教学内容。教学时可采用“构建问题场域，激活数学思维”“设计任务序列，促进思维进阶”“建立内化机制，融通数学思维”等策略，加深学生对知识本质的理解，促进学生高阶思维的自然生长。

【关键词】练习教学;一题一课;高阶思维;策略

练习是学生巩固知识、培养能力、锤炼思维的重要载体。受“知识本位” 观影响，目前练习教学呈现“重数量、轻质量;重技能、轻思维;重全面、轻提升”等问题。为此，笔者基于“一题一课”开展练习教学，引导学生通过对“一题”的深入研究，进一步理解知识、掌握方法，实现“学一题、透一点、通一类”的教学目标，促进学生高阶思维的发展。

基于“一题一课”的练习教学，聚焦主题，通过数学变式，进行结构化设计，为构建高效课堂提供了新思路。“一题一课”的练习教学，需要教师转变教学观念，深入研究“生”“题”“课”，激发学生学习数学的兴趣，培养学生的创新思维、逆向思维;提升学生的学习力，培育数学核心素养。

一、“一题一课”的练习教学内容选择

好的素材可以触发学生深度思考，好的“一题”应具备一定探究价值，具有通性通法，应基于教材又高于教材，是能让学生深度参与的核心问题。

（一）学生错误之处寻“题”

错误能折射出教师“教”或学生“学”中存在的问题。群体性错误或重复性错误，更能暴露学生的思维偏差。比如解决立体图形切割后体积与表面积的变化问题、阴影部分的周长与面积相关问题时，学生经常出现错误。如果能以“一题”为引线进行适当改编、重构，不仅能帮助学生攻克难点，还能促进学生发展思维，积累经验。

（二）知识迁移之处寻“题”

数学知识间有着千丝万缕的联系，从知识点联系密切、类型相同或者解题方法相通的习题中寻题，能达到“学一题，通一类”的效果。比如“用小正方形拼面积最小的长方形”和“用小正方体拼体积最小的长方体”等内容，可以整合成“一课”，引导学生整体理解，建立完整的认知结构。

（三）思维渗透之处寻“题”

有些习题蕴含着丰富的数学思想，如转化、化归、数形结合等对学生后续学习会产生重要影响。抓住数学思想方法“渗透点”来寻题，对习题进行适度加工，将附在“一题”上的数学思想显露出来，可以提高学生的数学核心素养。

二、“一题一课”的练习教学策略探寻

如何选择合适的“一题”进行开发，使其承载“一课”的研究价值？下面笔者结合“等积变形”一课，谈谈教学设想与实践。

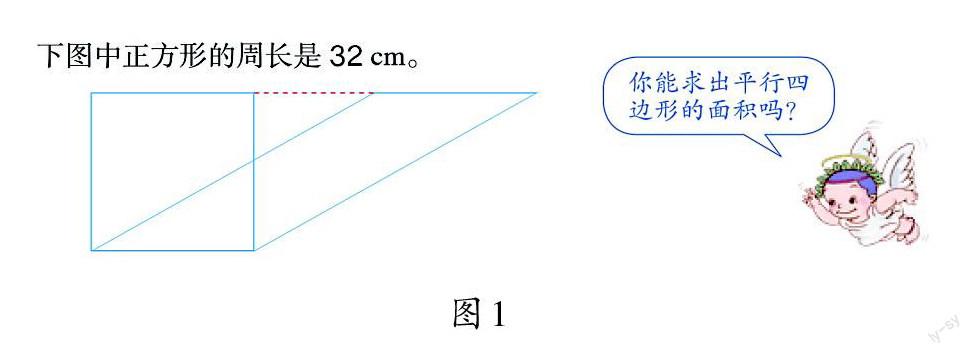
小学阶段平面图形教学中没有专门编排关于“等积变形”的教学内容，但配备的练习中很多问题都能借助“等积变形”来解决（如图1）。

大部分学生对“等积变形”停留在工具性理解水平，遇到图2这样的问题，学生很难主动从“等底等高”的内在本质中读取相关信息并解决问题。因此，我们试图根据学生的认知规律，设计教学序列，通过任务驱动，开放探究空间，引导学生发现其内在的等积变形方法，感悟转化的数学思想，发展几何直观。

（一）构建问题场域，激活数学思维

好的问题可以激活学生的思维，过于细碎的问题容易让学生产生认知惰性。因此，教师要精心设计问题，依托核心问题，激活学生的数学思维，促进学生展开独立自主的探究和个性化的思考。

1.提炼核心问题，激发思维内需

核心问题是一节课的“课眼”，是教师进行教学设计的核心。本节课根据教学目标及学生认知特点，提炼出的核心问题是“为什么三角形形状不同，面积却相等”，以此问题为基点不断聚焦、生成，激发学生不同的思维内需。

2.串联辅助问题，搭建思维平台

围绕核心问题设计相应的辅助问题，用符合学生的认知规律和知识形成的逻辑顺序的问题，串成问题链，为学生的思维发展提供“支架”，有助于学生全面、深入地思考。如本节课构造平行线环节，教师通过问题串“为什么要添这条线？这条线与哪条线平行？找到平行线有什么好处？如何进行面积的转化……”帮助学生理清思路，找到问题解决的突破点。

（二）设计任务序列，促进思维进阶

教学时要在相对开放的情境中，创设一些挑战性学习任务，让学生经历操作、观察、思考、交流等数学活动，引导学生进行自主、高效的探究。探究过程强调生生互动、师生互动，引导学生探究知识本质，积累经验，促进思维进阶。

1.任务驱动，激活经验

奥苏伯尔曾说过：“影响学习最重要的因素是学生已经知道了什么。”教學中，要关注学生的学习起点，通过创设低起点、高落点的任务，激活学生原有经验，调动学生思维，让学生在完成任务的过程中，自然习得知识，发展能力。

【教学片段】

（1）任务布置。

如图3中，大小正方形的边长分别是8cm和4cm，选3点连接成一个三角形。

①画一画：找到和你所画三角形面积相等的三角形，画在同一副图上，涂上阴影，并算出面积。

②想一想：你画的两个三角形为什么面积相等？

（2）汇报交流。

先收集展示学生典型作品，然后全班学生分享交流想法。（如图4）

（3）总结提炼。

思考：为什么这些三角形面积相等？

小结：等底等高的三角形面积相等。

本环节创设开放的任务情境，接纳学生之间的差异，引发学生多层次思考。一方面强化学生对三角形底、高等概念的理解。另一方面，通过学生在问题解决过程中生成丰富的感知材料，引发对三角形变形与面积变化之间关系的思考。学生在完成任务时呈现出不同的思维水平，让个人模糊的认识在全班交流中逐渐清晰。

2.动静融合，直击本质

感悟数学本质是学生深入思考的表现，但学生在学习新知时，易受无关因素干扰而忽略知识本质。因此教学中要借题发挥，让学生充分经历自主探索解决问题的过程，通过化繁为简、动静融合等方式突出知识的本质。

【教学片段】

师：请在图5中，找出和△AGD面积相等的三角形。

生：△AGC、△AGB、△ABC、△BCG。

师：这道题中等高怎么理解呢？

生：AG和BD是平行线。平行线之间的距离处处相等。

师：如果要继续画和他们面积相等的三角形可以怎么做？

生：只要底AG不变，顶点D在直线BD上移动，得到的三角形面积都相等。

（几何画板演示，如图6，教师有意识地在分别形成锐角三角形、直角三角形、钝角三角形时稍作停顿，引导学生观察。）

师：观察三角形的变化，有什么发现？

生：这些三角形形状不同，但底和高相等，面积也相等。

师：如果以GD为底，怎样快速找出与△AGD面积相等的三角形？

教师用课件演示以GD为底时，与△AGD面积相等的三角形画法（如图7），师生共同小结等积变形的方法。

本环节动静融合，让学生经历从图形变化中提炼出“等积变形”模型的过程，提升学生透过表面看本质的能力，通过动态的演示，突破“变与不变”的思维局限，发展学生的几何直观。

3.小题大做，深化模型

“就题论题”容易造成思维的固化，发展高阶思维要注重培养学生的思辨能力。教学时要充分挖掘习题的价值，借助一题多变、一题多问、一题多用等，引导学生进行深入的研究，实现知识的融会贯通。

【教学片段】

（1）对比优化。

学生独立思考、尝试求△BGE的面积，然后四人小组交流汇报。

生：我是先用大正方形的面积加梯形的面积算出整个图形的面积，然后减去空白部分△ABG和△BDE的面积，结果是32cm2（如图8）。

生：我把大三角形分成三个小三角形，分别求出每个小三角形的面积再相加，也是32cm2（如图9）。

生：我发现△BGE和△BGC面积相等，直接用8×8÷2=32cm2。

师：为什么△BGE和△BGC面积会相等？

生：连接CE，CE和BG是一组平行线，将点E移动到点C，那么△BGE和△BGC的面积相等，恰好是大正方形面积的一半，是32cm2（如图10）。

师：你是怎么知道这两条对角线是相互平行的？

生：因为正方形靠在一起，对角线的倾斜度一样，都是45度。

师：真会观察和思考。找到这隐藏的平行线有什么好处？

生：根据平行线特点，移动顶点时，三角形的高不变，就能进行面积转化了。

（几何画板再次演示：拉动顶点，再一次引导学生观察等积变形过程。）

小结并板书：找平行线，移动顶点。

（2）变化正方形大小，感受三角形面积变化。

师：如果右边正方形的边长减少或增加，那么三角形的面积会发生怎样的变化？

学生猜测并说理，教师进行几何画板演示（如图11）。

生：因为平行线的位置和大正方形的大小都没有变，所以三角形底和高都不变，面积也不变。

师：看来小正方形的大小改变不影响三角形面积。你还有什么想问吗？

生：左边正方形的大小发生变化时，三角形面积会不会变呢？

生：如果左边大正方形的大小发生变化，三角形底和高都会变化，所以面积也会变化。

（3）习题变式，巩固模型。

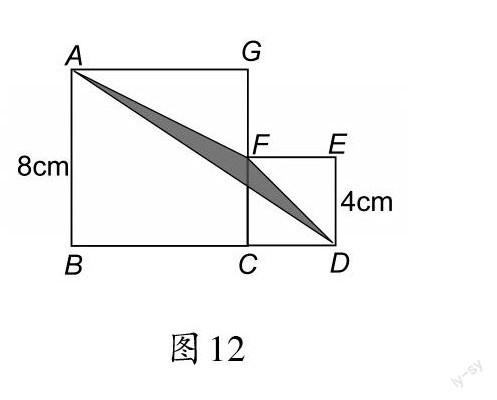
学生自主计算△AFD面积（如图12）。

结合同一幅图，经历从找平行线到自主构造平行线的过程。同一素材多次利用，不断打破学生的认知平衡，帮助学生把前面环节中内化的模型外显出来，让思维得到延续。一题多解，让学生既发散了思维，又体验了“等积变形”的便捷。一题多问，通过对“正方形的变化引起三角形面积的变化”进行思辨，深化对等积变形本质的理解。

（三）建立内化机制，融通数学思维

数学的学习是探索、发现和再创造的过程。因此要特别重视学生对知识的对比、联结、延伸等，有效建立内化机制，给学生交流、反思的机会，优化认知结构，促进思维的融通。

1.由此及彼，迁移“拓”思维

“一题一课”重要的目标是“学一题，透一点，通一类”，因此要注重知识迁移，引导学生将得到的结论和方法推广到别的习题中，激活关联思维。

【教学片段】

拓展习题1：图13中，已知长方形ABCD中，AB=6cm，AD=10cm，求四边形EFGH的面积。

生：把四边形EFGH分成两个三角形，顶点E、G分别往下移，变形成一个大三角形（如图14），求出面积是6×10×6÷2=30cm2。

生：△EHF的面积是长方形ABFH面积的一半，△HFG的面积是长方形HFCD面积的一半，所以涂色部分是长方形面积的一半。

拓展习题2：图15中，四边形ABCD的周长是57厘米，且点O到四条边的距离都等于6厘米。那么四边形ABCD的面积是多少？

小组汇报（如图16）：把四边形ABCD分成四个三角形，因为△OAB、△OAD、△OCD、△OBC的高都是6厘米，所以我们可以把4个三角形的底移到一起，变成一个大三角形（如图17），面积是57×6÷2=171cm2。

师：看来利用“等积变形”，可以把复杂图形转化成简单图形。

以上过程，学生经历了自主迁移等积变形基本模型的过程，将原四边形分割成多个三角形，既沟通了图形间的联系，又加深了对模型的理解，充分体现了思维的灵活性。

2.反思联结，融通“促”建构

教学中要注重挖掘知识间的内在联系，引导学生通过反思联结，纵向拉伸、横向贯通，不断将新知纳入原有认知结构中，实现数学思维由浅入深的建构。

本节课在回顾环节以“是不是只有三角形才能进行等积变形”引发学生思考，丰富学生对等积变形内涵的思考，让学生借助微课整体梳理，從等面积变形（梯形和平行四边形的等积变形、平面图形的割补转化）到等体积变形（铁块熔铸问题、排水法求体积问题），自然地实现了知识的融通与思维的生长。

基于“一题一课”，选择简约的素材，设计挑战性任务，提炼核心问题，可推进学生对知识本质的深刻理解，促进学生高阶思维的自然生长。

参考文献：

[1]鲍善军.一题一课：指向高阶思维能力培养的教学策略研究[J].小学教学参考（数学），2020（6）.

[2]邵珠利.一题一课在习题教学中的实施策略[J].教学月刊·小学版（数学），2016（6）.

[3]史宁中.推进基于学科核心素养的教学改革[J].中小学管理，2016（12）.

（浙江省杭州市钱塘区新湾小学   311228）