基于SOLO分类理论的一题之思
田秋月 谢琰翡

【摘 要】教师结合SOLO分类理论,分析六下年级学生在解决一道题的过程中所反映的思维水平层次。研究发现:多数学生处于关联结构水平,思维较广、深度不足。对此,教师得出“方程、算术殊途同归”“理清思路,夯实基础”两个维度的结论,提出“分化问题步骤”“转化信息表征”“强化关联结构”这三点建议。
【关键词】方程;思维层次;SOLO分类理论;实证研究
一、问题的提出
随着《义务教育数学课程标准(2022年版)》的颁布,“方程”即将走出小学教学内容范畴。方程是问题解决的常用方法,将它取消也会给教学中带来一些疑惑:(1)学生在解决问题时喜欢用方程还是算术方法?(2)影响学生选择使用解题方法的因素有哪些?(3)学生使用哪种方法更能更准确、高效地解决问题?(4)不同方法所体现出的思维层次是怎样的……笔者试图对这些问题进行研究,为后续教学活动中应采取的应对措施提供参考。
二、研究的设计
(一)研究对象
笔者以SL校六年级两个自然班共71名学生为研究对象,开展了聚焦一道题的调查。研究对象为使用浙教版教材的学生,他们从四年级下册开始进行了较为系统的方程相关知识的学习。
(二)测试内容
浙教版教材六年级下册《反比例应用问题》一课中有类似这样的一道练习题:“同学们爬山,上山的速度是60米/分,下山时从原路返回,速度是80米/分,往返一共用了70分钟。他们上山的路程是多少米?”教学浙教版教材四、五年级下册《列方程解题(二)》与《分数四则混合运算》时,在巩固练习中也会安排类似的题目。本题可根据两个数量关系,用两种思路:一是以“总时间”为等量的“两商之和”结构列方程解题;二是以“路程”为等量的“积”相等列方程解题。当学生学习浙教版教材五年级下册的《工程问题》、浙教版教材六年级上册《应用问题(一)(二)》之后,又会从“工程问题”的角度结合“分数应用问题”的数量关系进行解题。此题又在浙教版教材六年级下册以“比例”的形式出现。综合运用整个小学阶段的所学知识,学生解决本题时可选的数学方法较多。
(三)评价工具
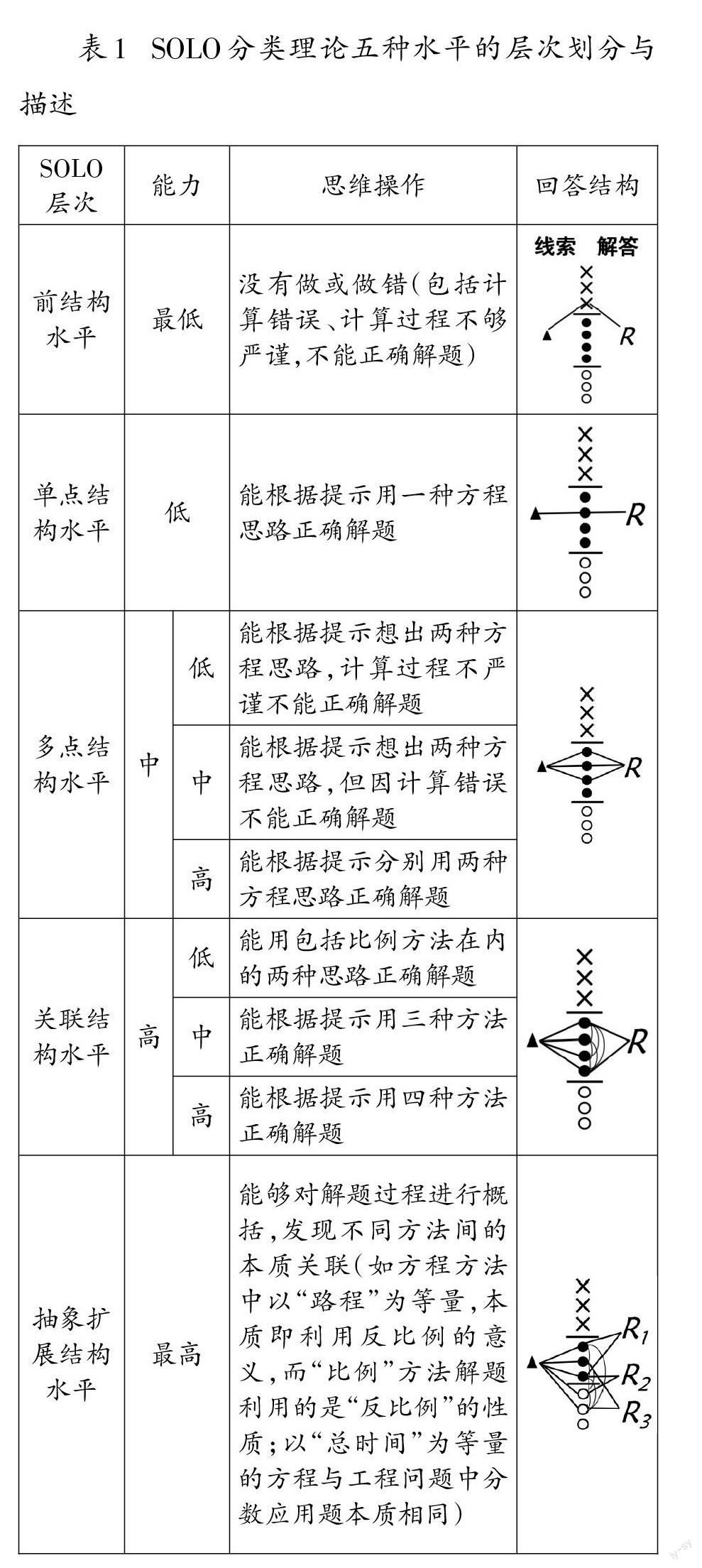
为了精准分析学情,笔者参考SOLO分类理论五种水平层次的划分,对照能力框架,确定本题具体作答水平层级,对掌握算术方法解题进行关联性评价(如表1)。
三、研究的结果
(一)总体表现
总体看来,5.6%的学生不能使用任何方法正确解答本题。仅从方法效用上看,“工程问题”思路的正确率最低、理解难度最大,其他三种方法解题正確率的差异不显著(如图1)。相比较而言,以“路程”为等量列方程解题的正确率略高于其他两种方法(如图2),达84.5%,且在方法的理解程度上(97.2%)存在明显优势。
(二)SOLO层次分析
依据SOLO分类理论,笔者对六年级71名学生解决此题的情况,按5种思维水平层次进行了分类统计(如表2)。
根据图3,结合表2,分析可得以下结论:
关联结构水平人数最多,约占测试总人数的60.6%。有94.4%的学生能用不止一种方法正确解答本题。大部分学生处于多点结构水平向关联结构水平的过渡的阶段,思维层级处于抽象扩展结构水平的比率相对较低。由此可见,从学生的思维水平层次来看,学生掌握一种或多种方法解题的能力强。然而,学生对解题过程进行概括,发现不同方法间的本质关联能力略有不足。
(三)典型作答分析
为了清晰地说明不同的思维水平层次,笔者从问卷中选取了对应的学生作答。
1.前结构水平。这部分学生主要表现为不理解题意及各个数据信息的含义,故作答不能体现正确的思路。被试学生中,1人作答区域空白,4人列出了不成立的数量关系(如图4-1、4-2)。
2.单点结构水平。研究对象中有4人只能读取单一信息、从一个维度进行思考。因对问题的考虑不够全面、严谨,不能从另一个维度用方程正确解题(如图5)。
3.多点结构水平。处于这一水平层次的学生有11人,主要表现为:①只能用方程的两种思路正确解题,但对“比例”方法束手无策,无法在提示与所学的知识间建立关联(如图6-1);②能根据提示“路程一定,速度与时间成反比”得到“时间比”,但不能在“时间比”与题中条件“总时间70分钟”间建立关联(如图6-2)。
4.关联结构水平。处于这一水平层次的学生人数最多,有43人。说明就本题而言,超过总数一半的学生已经达到高认知思维水平,不仅能用“比例”方法解题,还能清晰地列出“工程问题”方法的对应数量关系(如图7)。原因有两点:①作为一道基础练习题,虽然方法很多,但难度不大。② “比例”方法解题的关联性较强,能掌握“比例”方法解题的学生至少也能理解另外三种方法中的两种。
5.抽象扩展结构水平。达到这一思维水平的学生不仅能用四种方法正确解题,还能对不同方法进行抽象、归纳、对比,提炼出方法间的关联与共性(如图8),这类学生的思维具有一致性、整体性和深刻性。
四、启示与建议
在上述测试问卷与调查数据中,通过SOLO分类理论分析不同学生在解答同一道题时所反映的思维水平层次,可得到如下启示。
(一)方程、算术殊途同归
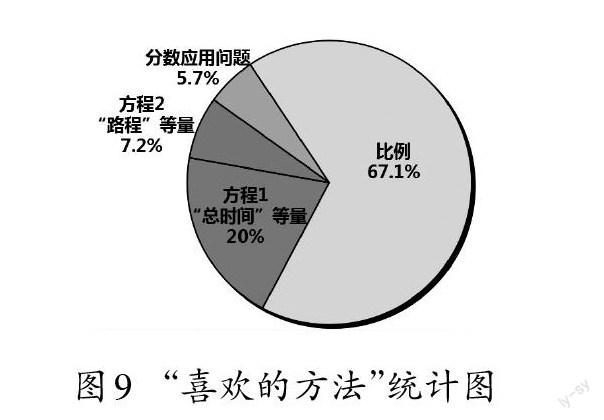
略高的正确率不能说明方程在解决本题中存在显著优势,且方程相关前期铺垫的时间、精力成本较高。“比例”方法因其思路简单、步骤清晰更易受六年级学生的欢迎,另一份有关学生主观维度的调查——“解决本题的四种方法中你最喜欢哪个”,也反映了此法的受欢迎程度(如图9)。有67.1%的学生更倾向于选择“比例”法解答本题,并表达了自己的选择理由(如图10)。因此,课堂教学中去“方程”可行。
(二)理清思路,夯实基础
怎样帮助学生更好地掌握、理解较受欢迎的“比例”方法呢?本研究继续分析不能使用此法解题的16名学生的作答,以此提出改进课堂教学的措施和建议。
1.分化问题步骤
用“比例”方法解决此类问题时,学生的困难在于没有整体性的解题策略,不能对信息和数据进行综合分析和考量。因此,课堂中,教师应帮助学生理清解决此题的步骤(如图11),让学生体会已知条件在对应解题环节的介入使用,理解分化出的四个解题小步骤串起来就是解决本题的过程。
2.转化信息表征
所有学生都能根据提示由“速度比”得到“时间比”,学生的共性困难在于识别不出模型——如何将“时间比”与已知条件“总时间70分钟”进行关联。此时需要用可视化的工具帮助学生理解:用线段图将计算时间的问题转化为“按比例分配”的模型,再往前追溯,实质又为“归一问题”(如图12)。
即使是六年级的学生,使用线段图转译信息也有难度。因此,在三年级第一次学习“归一问题”时,让学生尝试将文字表述的题转化成线段图再进行解释、表征具有十分重要的意义。
3.强化关联结构
思维水平处于由关联结构向抽象扩展过渡阶段的学生人数的急剧下降,说明课堂教学中还应关注学生分析问题的能力,帮助学生从看似不相关的问题中抽象、提炼出问题的共性模型,从而对症下药地选用合适的解决问题的方法。如同样用画图法解决“鸡兔同笼”问题,可用面积图(如图13)呈现思路,而此图又可结合不规则图形面积的转化进行解释(如图14),以此强化学生对不同问题、不同情境的整体性和深刻性认知。
基于SOLO理论分析学生解决问题的情况,可有效地反映同一道题不同学生的思维水平层次,评价不同学生的学习质量,为课堂教学中培养学生深刻理解、关联运用小学阶段数学知识解决问题的能力提供建议。
(浙江省杭州市胜利实验学校 310008)

