类比在初中数学概念教学中的应用
陈琴

【摘要】类比推理,属于逻辑推理的范畴。类比是分析与探索初中数学知识的重要方法之一。在初中数学中,概念、原理和基本性质是学好数学的基础,本文谈谈类比在概念、定理和基本性质教学中的应用。
【关键词】初中数学;类比;概念教学
发展学生核心素养是现代教育改革与发展的主要趋势之一。无论是中小学阶段的十大数学核心概念还是高中阶段的六大数学核心素养,都将逻辑推理能力单独列出来。而逻辑推理能力包括了三大内容:类比、归纳和演绎。
概念、原理和基本性质是数学教学中的核心内容,在数学教学过程中,让学生通过一些熟悉的事物进行合理的类比,以完成学习内容。学生如果能牢固掌握概念和原理,就可以运用逻辑推理能力解决新问题,从而提高其思维能力。但是,在现实教学中我们经常在“时间紧,内容多”的情况下忽略了概念教学,匆匆而过。这是本末倒置的,笔者在多年的教学经验中获悉,概念非常重要,必须认真设计好每一节概念课。本文笔者将探讨类比在概念教学中的一些应用。
一、情景类比,体验新识的乐趣
对于一些抽象,学生难以理解的概念,教师可以设计一些学生
熟悉且具有趣味性的故事情景,让学生在良好的氛围中轻松学习掌握抽象枯燥的概念。例如,八年级(下)学生开学学习“函数”,这是一个非常抽象,非常难理解的概念,笔者查阅了很多书籍,终于在《趣味数学》这本书中看到了它是这样讲解“函数”这个概念的:孙悟空大战牛魔王。孙悟空师徒几人因为要过火焰山,需要借助芭蕉公主的芭蕉扇,而芭蕉扇在牛魔王手上,所以只有战胜牛魔王才能拿到芭蕉扇,牛魔王虽然不是孙悟空的对手,但是,他会变,第一次变成一只白鹤,飞走了,孙悟空一看,马上变成一只凤凰,凤凰可是百鸟之王,白鹤当然斗不过凤凰;第二次牛魔王变成了一只香樟,假装在吃草,孙悟空立刻变成了一只猛虎,扑了过去;第三次牛魔王变成一头狮子,反过来擒猛虎,悟空一看,变成一只巨象,用长长的鼻子卷狮子;牛魔王没办法,只能拿出绝招,显身大白牛,悟空身体变得高万丈,拿金箍棒朝牛魔王打去。首先,我们从这个“变”字谈起,孙悟空和牛魔王都能变,我们要从变化的观点来研究数与量之间的关系。牛魔王因为打不过孙悟空,所以想尽办法逃走,因此先变,而孙悟空总是跟随着牛魔王的变化而变化的,并且这种变化有一定的原则。在一个变化过程中,发生变化的量称为变量,始终不变的量称为常量,所以在这个故事中,牛魔王和孙悟空都是变量,牛魔王总是先变,称为自变量,孙悟空是随着牛魔王的变化而变化的,称为函数,唐僧始终不会变,称为常量。后来在讲解“函数”这个概念时,笔者就用这个故事类比“函数”,果真收到了不错的效果,打破了外界给予学生的对函数的恐惧和茫然感,从而自然的过渡到新课讲解环节。
二、新旧知识类比,实现知识的迁移
纵观初中三年数学概念、定理中有相当多的知识和旧知识,无论在形式上还是实质上都非常相似,所以在教授新知时,教师可以引导学生将新知识与学过的知识进行类比,不但可以达到温故而知新的效果,还可以发现新知识。例如:在教授八年级(上)分式的概念时,教师可以让学生先回忆分数的有关概念性质,然后再引出分式的概念,与分数类似,分式的分母也不能为零,所以当分母不为零时,分式才有意义.类比分数的性质,让学生也可以猜测分式的性质。我们可以看出,分式与分数不仅形式上类似,性质也相似,所以只要让学生先复习分数的有关概念性质,也就可以很容易掌握分式的概念和性质了,从而实现知识的迁移。又例如:在教授九年级(下)相似三角形时,教师可以先让学生复习全等三角形的有关性质与判定方法,再过渡到相似三角形的学习,这样自然而然实现知识的迁移。还有,讲解不等式的性质时,可以类比等式的性质,讲授不等式的解法时可以类比一元一次方程的解法;讲授二次函数的相关概念性质时可以类比一元二次方程等等。新旧知识的类比,不仅可以让学生感受到数学的发展,也实现了知识的迁移。
三、数形类比,让知识得以升华
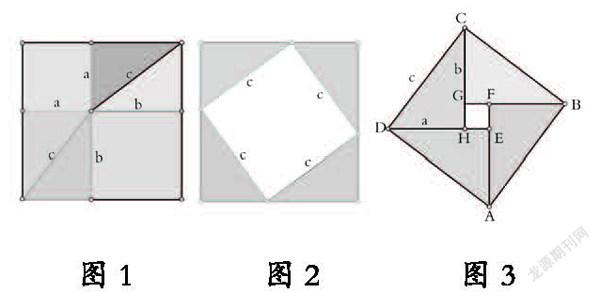
数形结合是初中生学习数学方法中非常重要并且很常用的一种。教师在教学中让学生将数与形进行类比,能让学生更牢固的掌握知识,更深刻的理解数学概念或性质。例如:将九年级(上)的一元二次方程根的判别放到了二次函数的图象中时,学生会发现原来两者之间是有联系的,这时就能更深刻的掌握一元二次方程和二次函数的性质了。又例如,八年级(下)勾股定理的探索,教师一般先通过一些特殊图形带领学生得出结论,即直角三角形两条直角边的平方和等于斜边的平方。我们知道这样得出的结论是不严谨的,没有经过证明的定理是不能用于证明其他题目。教师可以带着学生用几何图形进行证明,这一步绝对不能省,不能因为课时紧而省略。我们来看看用图形证明勾股定理其中两种方法。方法一:做4个直角边长分别为a、b(b﹥a)的直角三角形,斜边长为c,两个边长分别为a和b的正方形,拼成图1的大正方形,则大正方形的边长是(a+b),面积是a2+b2+4·ab。再做4个直角边长分别为a、b(b﹥a)直角三角形,斜边长也为c,和一个边长为c的正方形,拼成图2的大正方形,我们可以看出大正方形的边长也是(a+b),面积是c2+4·ab, 可以看出两个大正方形面积相等,整理得a2+b2=c2。方法二:如图3,做4个全等的直角三角形,直角边为a、b(b>a), 斜边为c,两个边长分别为a和b的正方形,拼成图1的大正方形,则大正方形的边长是(a+b),面积是a2+b2+4·ab。再做4个直角边长分别为a、b(b﹥a)直角三角形,斜边长也为c,和一个边长为c的正方形,拼成图2的大正方形,我们可以看出大正方形的边长也是(a+b),面积是c2+4·ab, 可以看出两个大正方形面积相等,整理得a2+b2=c2。方法二:如图3,做4个全等的直角三角形,直角边为a、b(b>a), 斜边为c,拼成图3所示形状,每个直角三角形的面积等于ab. ∵ RtΔDAE ≌ RtΔABF,∴ ∠EDA = ∠FAB.∵ EDA + ∠EAD = 90°,∴ ∠FAB + EHAD = 90°;∴ 四边形ABCD是一个边长为c的正方形,它的面积等于c2.∵ GH =HE =EF=FG= b-a ,∠AED = 90°.∴ 四边形GHEF是一个边长为(b-a),面积等于(b-a)2的正方形.∴(b-a)2=c2-4·ab∴ a2+b2=c2。
四、防止盲目類比,纠正学生容易产生的错误认识
采用类比可以让学生在学习中尝到许多甜头,所以他们乐意使用类比,但学生在使用类比时往往只根据形式类似就进行了类比,从而造成错误。例如:八年级(上)幂的运算中,积的乘方就是先的把积中的每一个因数分别乘方,再把所得的幂相乘。 (ab)n=an·bn当学生学习了积的乘方后,往往会把之前学过的完全平方公式给混淆了,会写成这样(a+b)2=a2+b2或(a-b)2=a2-b2,这就是简单的类比所造成的错误。又例如在学习了分式的基本性质后,在化简分式时常出现这样的错误,学生简单的把分子分母中的a约去,好像分式(a+2)/(a-2)学生化简后等于-1,这也是简单的类比,造成的错误。类似这种错误,学生在整个初中阶段会经常出现,所以就需要教师在用类比法进行教学时,务必引导学生想通想透,不能盲目类比。
类比是数学方法论中最基本的方法之一,也是培养学生逻辑推理能力的其中一项,用好了能获得新的成果,但是要真正用好它并不容易,这需要教师的知识面广,并且能预知学生在学习过程中可能出现的错误,才能引导学生在类比中想通想透。又需要学生自己能够在教师引导下,自觉的探究、反思,最后形成自己的逻辑思维能力。
参考文献:
[1]陈显强.浅谈归纳法和类比法在数学中的应用[J].广东广播电视大学学报,1999,02.
[2]陆月华,周建平.类比法在数学教学中的应用[J].小学教学研究,2018,07.
[3]姚英.浅谈类比法在数学教学中的应用[J].赤峰教育学院学报,1999,3.
[4]黄晓菲.趣味数学[M].广东世界图书出版公司,2014,9.A111222F-54FD-42D8-A308-1781E4F26EE3

