基于信赖域算法的精馏塔优化

刘星伟，贾胜坤，罗祎青，袁希钢，2

（1 天津大学化工学院，天津 300354； 2 化学工程联合国家重点实验室（天津大学），天津 300354）

引 言

分离过程是化学工业生产过程中的重要过程，而精馏分离是化工生产过程中最主要的分离方法[1]。精馏塔的严格优化与设计对于降低精馏过程能耗，节约生产成本，减少生产过程的碳排放和环境污染具有重要意义[2-4]。

精馏塔优化设计的决策变量既包含回流比、压力、再沸比等连续变量，又包含总塔板数、进料板位置等离散变量，因此对精馏塔决策变量进行同时优化属于混合整数非线性规划(mixed-integer nonlinear programming, MINLP)问题，其优化求解面临很多困难。在传统的精馏塔优化工作中，往往直接将总塔板数和进料位置作为整数变量进行优化[5-7]。Viswanathan 等[8]假设回流流股和再沸流股同时进入多个塔板，并且采用0-1二元变量来表示流股具体进入的位置，构造了一种精馏塔级数优化的超结构模型，并在许多工作中都得到了广泛应用[9-11]。但是，对于此模型的优化仍然是MINLP 问题，后续研究者提出了多种方法，将0-1二元变量进行连续化松弛，以达到降低优化问题求解难度的目的。Lang等[12]假设流股可进入多个平衡级，采用可微分的微分分布函数来表示进入一个平衡级的流量占总流量的比例，从而使进料位置和总塔板数等整数变量转化为连续变量，实现了塔板数的连续化。Neves 等[13]受到Lang 等工作[12]的启发，不再采用微分分布函数，而是直接采用0-1 之间的分数代表进入一个平衡的流量占总流股流量的比例，再通过不等式约束使分数趋近整数，最终得到整数。Kraemer等[14]同样首先假设回流流股和再沸流股同时进入多个塔板，并且采用0-1二元变量来表示流股具体进入的位置，然后再松弛二元变量为连续变量，最后引入非线性Fischer-Burmeister 函数来驱使这些连续变量收敛为0-1二元变量值。

在上述精馏塔的优化工作中，研究者通过使进料流股和回流流股同时进入多个平衡级，建立进料位置和总塔板数优化的超结构。这种精馏塔模型的超结构较为复杂，因此很难应用到复杂精馏流程中。本文从结构优化的角度，将精馏塔优化中较为困难的进料位置和总塔板数优化转化为空间结构的分布优化，即在精馏段和提馏段预设多于需要的平衡级数，采用结构参数代表平衡级是否存在，再通过精馏段和提馏段的实际平衡级数来表示进料位置和总塔板数。

在结构优化的研究中，信赖域优化算法更常被用来求解优化问题。不同于线搜索优化算法，信赖域优化算法采用先步长、后方向的策略，其在当前迭代点的邻域内构造优化子问题，并逐步逼近原问题的最优解。信赖域算法具有很好的适用性和稳健性，并且可以保证优化的全局收敛性[15]，另外，信赖域算法可以方便地与流程模拟软件进行联用，因此，其在精馏塔优化中有许多优势。

本文从结构优化的角度对精馏塔进行建模，采用信赖域优化算法对模型进行优化，并搭建了流程模拟软件Aspen Custom Modeler 与Matlab 结合的优化方法。为了证明提出的优化方法的可行性和收敛性，本文采用该优化方法分别对单一精馏塔、直接精馏序列和部分热耦合精馏塔进行优化设计。

1 模型与优化算法

1.1 精馏模型

本文从结构优化的角度建立精馏模型，将总塔板数和进料位置的优化转化为塔板空间分布的结构优化，并用0-1二元结构参数表示塔板的存在性。如图1 所示，在精馏段和提馏段预先设置多于需要的平衡级数，每一个方框代表一个平衡级，当二元结构参数为1时，代表平衡级起到分离作用（灰色），取0 则表示平衡级不存在。这样，通过优化0-1 二元结构参数的分布，就可以实现对总塔板数和进料位置的同时优化，将精馏过程的优化转化为二元结构参数分布结构的优化。

图1 精馏塔结构参数模型示意图Fig.1 Schematic diagram of distillation column structure parameter model

为了避免优化求解0-1 二元变量的MINLP 问题，本文采用Dowling 等[16]提出的绕流效率模型将二元变量连续化。如图2 所示，图中L为液相流股，V为气相流股，其基本思想是为每一平衡级增加绕流流股，流入第j个平衡级的气液相流股，被分为两部分：一部分进入该平衡级进行分离；另一部分绕过该平衡级。进入平衡级的流量占总流量的比例则用绕流效率εj表示。再将该平衡级上的汽液平衡流股与绕流流股混合，就得到离开该平衡级的气液相流股。

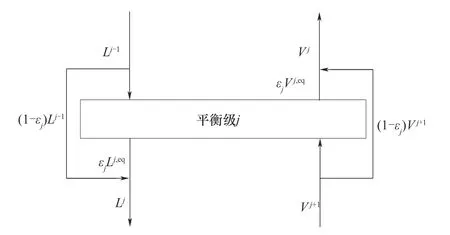
图2 绕流效率模型Fig.2 Illustration of bypass efficiency model

1.2 移动渐近线算法

在优化算法方面，本文采用信赖域优化算法中的移动渐近线法（MMA），其最早由Svanberg[17-18]提出，并被应用于机械工程的结构优化问题中[19-20]。该算法对于一个一般的非线性约束优化问题[式(1)]，在当前迭代点xk处采用子问题[式(2)]进行近似。

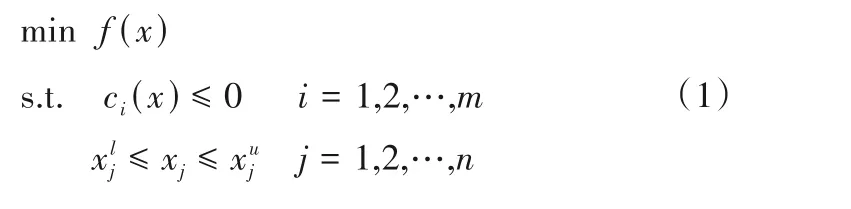
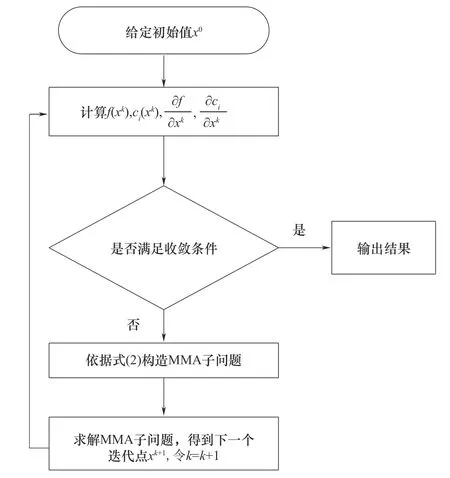
图3 MMA算法Fig.3 MMA algorithm

1.3 优化方法

MMA 算法仅需要目标函数值、约束函数值、目标函数和约束函数关于决策变量的梯度信息即可构造出子问题，求解子问题即可得到下一个迭代点，因此很容易和流程模拟软件结合使用。本文在Aspen Custom Modeler（ACM）中建立精馏模型方程，在Matlab 中执行MMA 优化算法，通过ACM 和Matlab 联用传输模型和优化算法之间的信息，具体的优化方法如图4所示。

图4 精馏塔优化方法Fig.4 Optimization method of distillation column

本文采用联立方程法进行精馏模型的求解，该方法可以较容易地获取优化所需要的梯度信息。但是，由于精馏塔的MESH 方程是一个强耦合的非线性方程组，为了解决其稳态解的求解困难问题，本文采用Ma 等[21]提出的虚拟瞬态连续性模型(PTC)来辅助精馏模型方程的求解。该模型引入虚拟持液量的概念，采用动态模拟方程来实现MESH 方程组的求解。当该动态模型方程积分至稳态时，即可以获得MESH 方程的稳态解。ACM 可以方便地输出优化所需要的信息，并将优化信息传入Matlab 执行MMA 的一步迭代过程。之后，优化算法将会给出下一个迭代点，将此迭代点传入ACM 中进行稳态模拟计算。若稳态模拟计算失败，则采用虚拟瞬态连续性方程进行动态积分，进而获得当前迭代点的稳态模拟结果。因为动态积分过程所需时间较长，因此优先执行稳态模拟过程，稳态模拟失败再执行动态积分过程，以减少模拟所需要的时间。重复以上迭代过程，直到满足收敛条件便可获得最终的优化结果。

2 算例分析

本文采用1.3 节中所提出的优化方法对3 个算例进行优化，优化的目标函数均为年度总费用（TAC）。TAC 由设备费和操作费构成，设备费根据精馏塔塔板数、塔径和换热器的换热面积计算，操作费由再沸器和冷凝器的换热量算出，具体计算公式可参考Jiang 等[22]的工作。每一个优化算例分别从5 个不同的初始点进行优化，以此说明所提优化方法的可行性及收敛性。

2.1 乙苯-苯乙烯二元混合分离

在本算例中，一个单精馏塔被用于分离乙苯和苯乙烯的混合物，混合物的进料情况如图5 所示，规定塔顶和塔釜产品的摩尔分数高于95%。因为苯乙烯在压力较高时易于发生聚合，因此塔顶的压力选为6 kPa。优化变量包括每一平衡级的绕流效率、回流比（RR）和再沸器的汽化分率（Vf）。本算例为每个塔节设置25 个平衡级，每个塔节有25 个绕流效率作为决策变量，因此该优化问题的决策变量数为52，约束个数为2。结合目标函数和精馏过程应满足的约束条件，可以得到式（3）所示的约束问题，该问题的结构同样适用于后面两个优化算例。

图5 乙苯-苯乙烯分离塔的结构Fig.5 Structure of ethylbenzene-styrene column

本文的优化初始值选择回流比为5，再沸器的汽化分率为0.5，绕流效率分别从5 个不同的初始点0.1、0.3、0.5、0.7 和0.9 进行优化，不同初始点的优化结果如表1 所示。表中的N1和N2分别表示精馏段和提馏段绕流效率之和，即精馏段和提馏段的塔板数。

表1 乙苯-苯乙烯分离塔的优化结果Table 1 Optimization results of ethylbenzene-styrene column

如表1所示，在5个不同绕流效率初始点的优化计算中，绕流效率ε都收敛到0 或1，因此，最终得到的塔板数为整数。绕流效率模型在不对分数绕流效率进行惩罚时，绕流效率仍趋于0 或1，Dowling 等[16]解释这一现象，在绕流效率为分数时，意味着存在一部分流股绕过塔板，此时的热力学效率较低，因此绕流效率趋于0 或1。许多应用绕流效率模型对精馏塔进行优化的工作中，最终都得到了整数绕流效率的优化结果[21,23-24]。该结果一方面说明了绕流效率模型的有效性；另一方面也说明移动渐近线法可有效找到该问题的最优值。另外，从不同的初始值进行优化，MMA算法均可找到该问题的一个局部最优值，说明MMA 优化算法的收敛性较好。图6给出了以绕流效率0.1 为初值时，N1（精馏段绕流效率之和）、N2（提馏段绕流效率之和）和目标函数TAC随迭代次数的变化。从图中可以看出，仅需要36次迭代即可得到最终的优化结果。

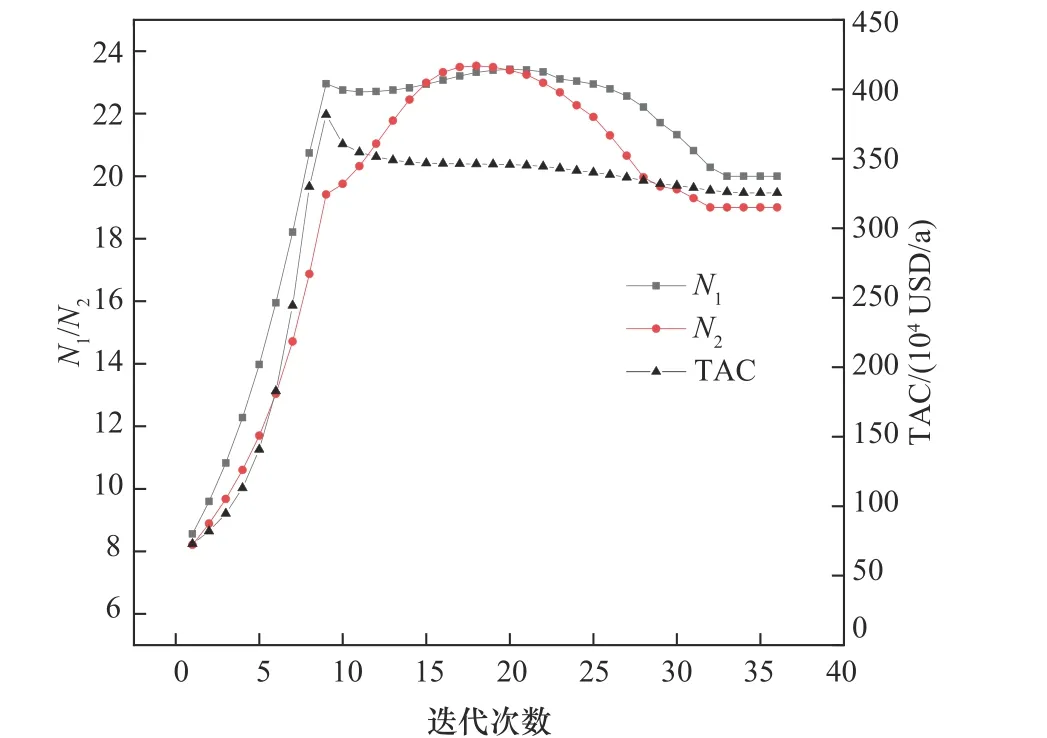
图6 N1、N2和TAC随迭代次数的变化Fig.6 Variation of N1,N2 and TAC with iteration

从5 个不同的初始点进行优化，最终优化结果并不完全相同，说明绕流效率模型有较多的局部最优解。通过枚举可以知道，该精馏结构的最优精馏段平衡级数为19，提馏段塔板数为18，回流比为6.48，塔釜汽化分率为0.8380，对应的最优TAC 为324.474×104USD/a。对比得到的5 个最优结果，虽然均未得到全局最优值，但与全局最优值相差较小，这说明MMA 优化算法用于精馏塔优化同样可以获得较好的结果。本方法无法保证获得全局最优解，但是具有较好的稳健性，为获得较好的局部最优解甚至全局最优解，可以从多个初始点出发进行计算，以选取最好的局部最优解。

2.2 直接精馏塔序列

直接精馏塔序列是分离三组元混合物的基本方法之一。在本算例中，采用直接序列对苯、甲苯和对二甲苯进行分离。产品的进料情况如图7 所示。本算例要求三个产品的摩尔分数不低于95%，塔顶的压力固定为1 bar（1 bar=105Pa），优化变量包括每个平衡级的绕流效率、两个精馏塔的回流比（RR1、RR2）和两个精馏塔再沸器汽化分率（Vf1、Vf2）。本算例仍为每个塔节设置25个平衡级，因此本优化算例包括3 个约束条件，104 个优化变量。表2 展示了最终的优化结果，表中的N1、N2、N3和N4的含义如图7所示。

图7 直接序列精馏塔结构Fig.7 Structure of direct sequence distillation column

如表2 所示，在5 个不同初始点的优化计算中，从不同初始值开始优化，绕流效率最终均收敛为0或1，相应的平衡级数为整数，这说明在本算例中MMA 优化算法同样可以找到局部最优解。本算例优化变量比2.1 节算例多一倍，在这种情况下，不同初始值均能收敛到局部最优解，说明MMA 优化算法的收敛性和稳定性较好。

表2 直接序列精馏塔的优化结果Table 2 Optimization results of direct sequence distillation column

2.3 部分热耦合的精馏过程

精馏操作所消耗的能量占化工生产总能量消耗的很大比例，部分热耦合的精馏过程常常被作为一种精馏设计的节能措施[25-30]。但是，由于部分热耦合精馏流程中存在质量和能量的耦合，因此求解难度增加。本节考虑对图8 的精馏结构进行优化，进料为正己烷、正庚烷和正辛烷。两个精馏塔的塔顶压力均固定为1 bar，三个产品纯度均要求摩尔分数不低于95%。优化变量包括每个平衡级的绕流效率、两个精馏塔的回流比（RR1、RR2）、第二个精馏塔的再沸器汽化分率（Vf）以及进入第二个精馏塔精馏段的气量占第二个精馏塔提馏段气量的比例（Sf）。本算例仍为每个塔节设置25 个平衡级，因此本优化算例包括3 个约束条件，104 个优化变量。表3 展示了最终的优化结果，表中的N1、N2、N3和N4的含义如图8所示。

图8 部分热耦合精馏结构Fig.8 Structure of partially thermally coupled distillation process

如表3 所示，在5 个不同初始点的优化计算中，不同初始值的优化结果的绕流效率均为0或1，这说明绕流效率模型在具有热耦合精馏结构中依然有效。5 个不同的初始值均获得了优化结果，这一方面说明所提优化框架稳健性较好，对于含有热耦合结构的优化过程依然有效，另一方面说明MMA 优化算法有较好的收敛性，在含有热耦合结构的优化中依然有效。

表3 部分热耦合精馏过程优化结果Table 3 Optimization results of partially thermally coupled distillation process

3 结 论

（1）从结构优化的角度，将精馏塔总塔板数和进料位置的优化转化为二元结构参数分布结构的优化，并结合绕流效率模型将二元离散变量转化为连续变量。该模型可以降低精馏塔模型的复杂程度，实现对总塔板数和进料位置的同时优化。

（2）采用联立方程法对精馏塔进行建模，采用虚拟瞬态连续性方程来辅助精馏稳态模拟计算，实现了精馏塔决策变量的同时优化。分别对一个单一精馏塔、直接序列精馏塔和热耦合结构精馏塔进行优化设计。结果表明，虚拟瞬态连续性方程可有效辅助稳态模拟的计算。

（3）结合MMA 算法的特点，将Aspen Custom Modeler 和Matlab 耦合链接，充分利用了Aspen Custom Modeler 的模拟能力和Matlab 的优化计算能力。该优化方法可保证本文3个优化算例的正常运行，体现了该方法的稳健性。

从优化算例来看，初始值的选取会对优化结果产生影响，如何选取初始值以获得更好的结果值得进一步探究。本文建立的优化方法对许多优化算法同样适用，因此，不同优化算法在精馏塔优化中的表现是未来一个值得研究的方向。