基于数据驱动的气动柔性关节Takagi-Sugeno模糊系统建模与预测控制
陈 诚,黄 剑,刘 磊,伍冬睿
(华中科技大学人工智能与自动化学院,湖北武汉 430074)
1 引言
近年来,随着机器人技术的发展[1-2],机器人已经成功应用到了航天、工业、康复医疗、仿生学等各个领域[3].而人机交互过程对机器人机构的柔顺性和动作的安全性提出了挑战.由于缺乏物理柔顺器件,电机驱动的机器人在安全性和舒适性上有所欠缺.气动肌肉作为一种本质柔顺的新型驱动器,具有高负载/自重比、清洁环保、成本低等优点[4],近年来,吸引了大量相关研究[5].然而,气动肌肉的参数时变性和磁滞性等非线性特性使气动系统的高精度控制成为一个难点.
近年来,研究者们提出了许多针对气动系统轨迹跟踪控制问题的算法.文献[6]针对氢驱动的气动肌肉驱动器,提出了一种模糊自整定比例积分微分(proportion integration differentiation,PID)控制器,在响应速度、稳态误差、超调等方面相比传统PID控制器都有显著提升.文献[7]将滑模控制成功应用于对拉式气动肌肉驱动的关节.文献[8]在动态面控制的基础上引入非线性干扰观测器,消除了模型不确定性和外界扰动的影响,提升了控制精度.以PID控制为代表的无模型控制算法实现简单、应用广泛,然而通常鲁棒性差,难以提升控制精度,且稳定性无法在理论上得到保证.而滑模控制等基于模型的控制算法,其控制性能则依赖于系统模型的准确性.
预测控制作为处理约束优化问题的先进控制算法,能够综合利用目标系统的历史信息和模型信息,针对给定的性能目标函数不断地对系统进行滚动优化,并根据实际测得的输出对象对系统进行校正,具有自适应能力、鲁棒性和在线优化的能力,近年来在复杂非线性系统已得到了广泛应用[9].文献[10]利用区间二型Takagi-Sugeno(T-S)模糊模型来描述具有参数不确定性的非线性被控对象,提出了一种反馈预测控制算法.文献[11]提出了一种自适应T-S模糊预测控制算法,T-S模糊系统的参数可根据跟踪误差在线调整.现有的预测控制方法中,T-S模糊建模多是在工作点附近对非线性被控对象进行线性化处理建立预测模型,然后针对分区线性化模型依据线性系统预测控制的思路进行控制器设计.基于线性矩阵不等式(linear matrix inequalities,LMIs)的方法常被用来计算控制器增益,预测控制的性能指标函数为LMIs提供约束以提升控制性能.这类优化问题的求解和矩阵逆运算都增加了在线运算的计算量,控制系统的复杂性往往较高.
上述方法中,当目标系统的非线性和不确定性很强时,基于专家知识往往难以建立准确的T-S模糊系统模型.而基于数据驱动的建模方法不需要被控对象的先验知识,仅利用输入输出数据便可确定模糊系统的隶属函数和模糊规则,近年来基于数据驱动的模糊系统建模研究大量涌现[12].文献[13]将T-S模糊结构和多元高斯核作为隶属函数合并提出了一种动态简约模糊神经网络.文献[14]提出了一种自动进行T-S模糊系统结构辨识和参数优化的方法,并能以可接受的精度找到最优的规则数.此外,一些机器学习的方法也开始被引入T-S模糊系统建模.文献[15]首次提出用机器学习的方法训练T-S模糊系统并成功应用于回归问题,通过多组实验验证了应用此类方法训练的T-S模糊系统具有较强的泛化性能.文献[16]则将统一正则化和批量归一化结合到了T-S模糊系统回归器的训练中.然而,现有的关于数据驱动建模方法在实时控制问题中的应用研究较少.此外,T-S模糊系统存在模糊集和规则数冗余和近似的情况,进行模糊集和模糊规则的简化,可提升计算效率,便于在实时控制中应用[17].
针对以上问题,本文提出了一种基于数据驱动的T-S模糊系统建模和预测控制方法,主要工作归纳如下:1) 结合多种机器学习训练算法,应用MBGD-RDA算法对T-S模糊系统进行建模,并基于相似性度量,进行模糊集剪枝和模糊规则简约,实现T-S模糊系统结构的简化;2)提出了基于T-S模糊系统的单层神经网络(single layer neural network,SNN)预测控制器且控制系统的稳定性得到了保证;3)通过仿真和实验验证了本文提出的方法的有效性:仿真结果表明,数据驱动建模的T-S模糊系统可准确预测被控对象的动态性能,且在模糊集和规则减少的情况下仍能保持较高的预测精度;实验结果表明,所提出的控制器相比传统的模糊逻辑控制器,轨迹跟踪控制精度显著提高.
2 气动柔性关节动力学建模
气动柔性关节的原理如图1所示.
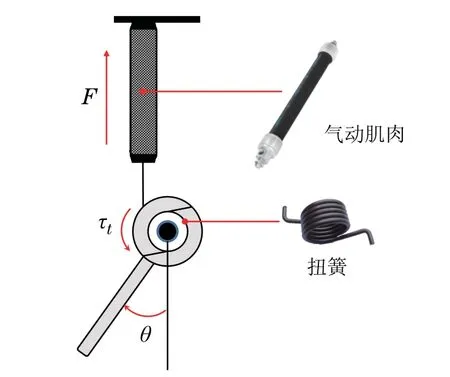
图1 气动柔性关节原理图Fig.1 Schematic diagram of the pneumatic flexible joint
该关节的驱动部分由一根气动肌肉和一个扭簧组成,气动肌肉通过钢丝绳与下方的圆盘连接,扭簧安装于圆盘转轴的轴心处.当气动肌肉充气收缩时,通过钢丝绳对圆盘产生向上的拉力F,带动关节顺时针旋转,与此同时扭簧旋转压缩,产生逆时针方向的力矩T,与气动肌肉产生的力矩形成对抗;当气动肌肉放气伸长时,气动肌肉拉力F减小,在扭簧回复力矩的作用下,关节逆时针旋转恢复到初始位置.
根据文献[18],建立柔性关节动力学模型
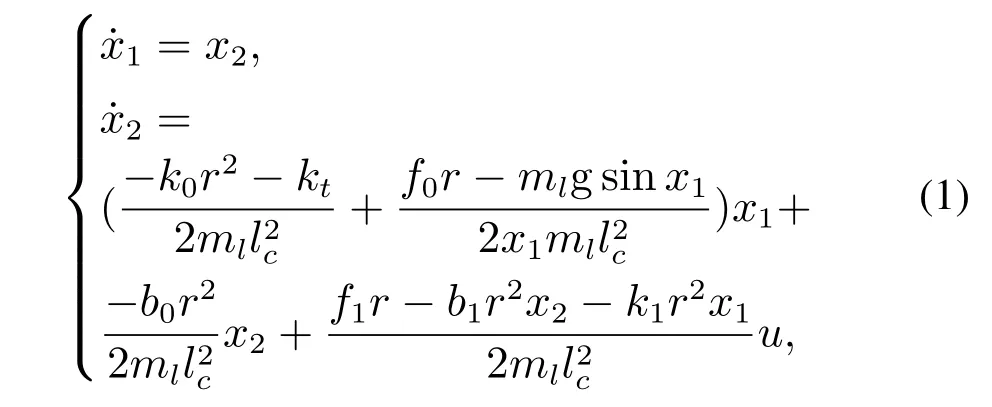
其中:x1和x2为状态变量,表示关节旋转角度θ和角速度;p表示气动肌肉内部气压,与控制信号u为线性关系;p0表示气动肌肉气压状态的临界值;k0,k1,b0和b1是气动肌肉状态相关的参数;kt是扭簧刚度;ml为关节摆杆的质量;lc为摆杆的质心到关节圆心的距离;g为重力加速度;r为圆盘半径.模型参数取值如表1所示.
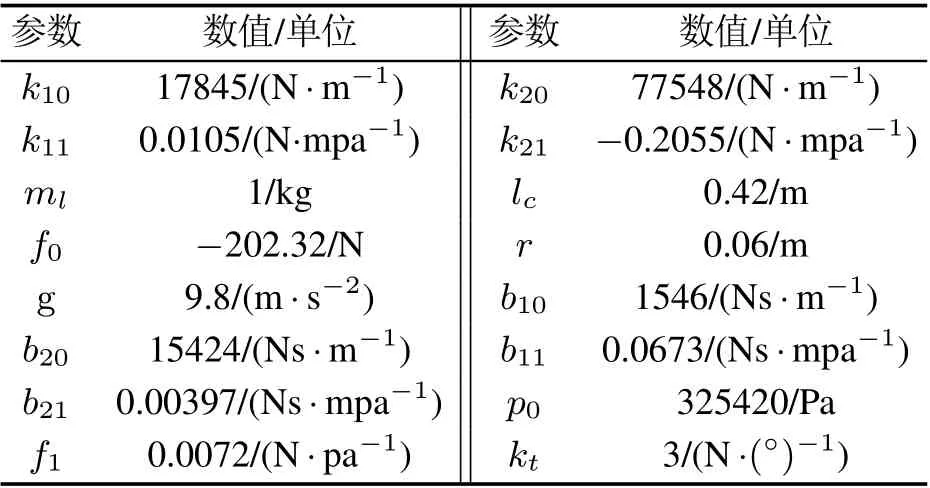
表1 气动柔性关节模型参数表Table 1 Model parameters of the flexible joint
3 基于T-S模糊系统的预测控制器设计
3.1 T-S模糊系统

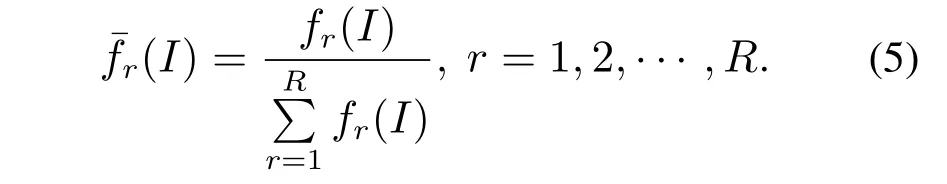
最终,T-S模糊系统的输出可表示为
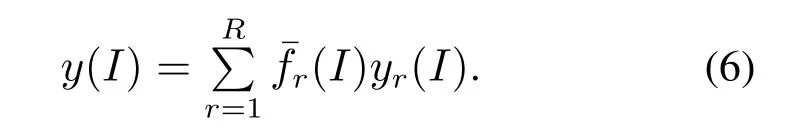
3.2 数据驱动的T-S模糊系统建模
考虑使用数据驱动的方法来对T-S模糊系统进行建模,逼近气动柔性关节的动力学模型.给被控对象输入开环的正弦控制信号驱动关节运动,采集控制信号和运动信号构建T-S模糊系统的离线训练数据集.数据集输入为当前时刻的控制信号和前两时刻的运动轨迹,u(k+1),y(k),y(k-1),输出第p-1 时刻后的运动轨迹,y(k+p).设置T-S模糊系统的结构,包括隶属函数个数和对应规则数,使用MBGD-RDA算法对系统进行离线训练[15].
采用梯度下降的方法在线优化T-S模糊系统的隶属函数参数cr,n,σr,n和后件参数ar,n.设代价函数为

3.3 T-S模糊系统简化
上述T-S模糊系统的隶属函数个数和规则数是人为设定,可能存在冗余或者相似.因此,本节基于相似性分析的方法,进行模糊集和模糊规则的删除和合并.
A和B为两模糊集,定义模糊集A和模糊集B的相似性计算方法如下:
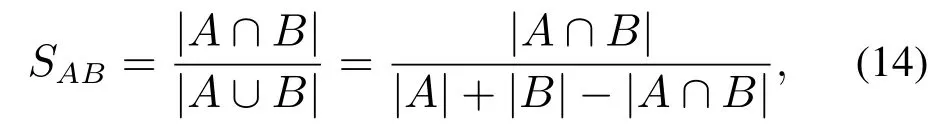
其中:∩和∪分别表示交集和并集;|·|表示模糊集的大小.由式(14)可知计算模糊集的相似度需要计算两个模糊集交集和并集的大小,而本文使用的高斯函数的边界为非线性,其交集和并集区域大小难以计算,因此考虑先使用梯形函数对高斯函数进行近似描述,再以梯形函数的相似性来衡量高斯隶属函数的相似性.
3.3.1 模糊集相似性度量
一个高斯隶属函数可以用一个梯形函数近似.蓝色曲线为高斯隶属函数G(x),红色为近似的梯形函数T(x),如图2所示.
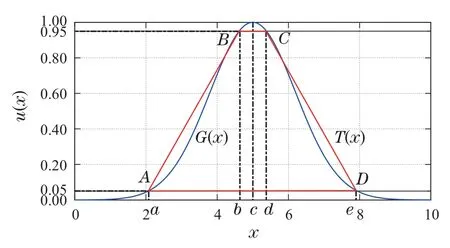
图2 模糊集的α-截集Fig.2 α-cut of a fuzzy set
高斯函数为
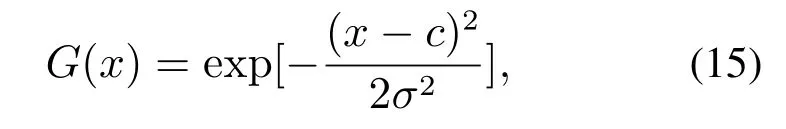
梯形函数表示为

其中参数a,b,d,e根据引入的两个α-截集确定.
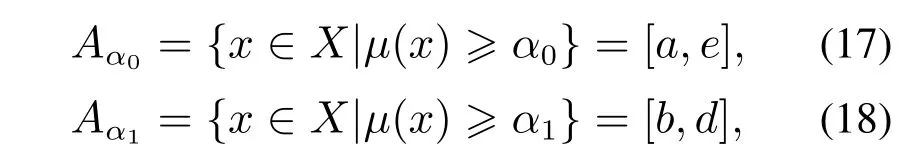
其中:α0=0.05,α1=0.95.
由以上分析可知,一个梯形函数可由a,b,d,e四个参数确定,函数的中心为c=0.5(a+e).下面通过分析梯形函数的相似性来度量对应模糊集的相似性.
以两个梯形函数T1,T2为例,其对应的参数分别为a1,b1,c1,d1,e1和a2,b2,c2,d2,e2.假设c2>c1,分3种情况讨论.
情况1如图3所示,模糊集T1包含模糊集T2,T1⊂T2.两模糊集的相似度的计算方法如下:
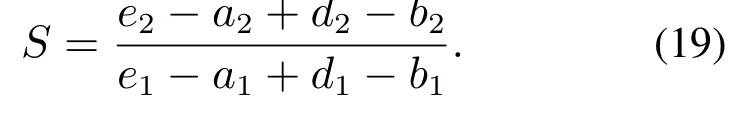

图3 情况1下两个模糊集的相似度Fig.3 Similarity of two fuzzy sets for case 1
情况2a如图4所示,模糊集T1和模糊集T2底部有重合,顶部无重合部分.两模糊集的相似度的计算方法如下:
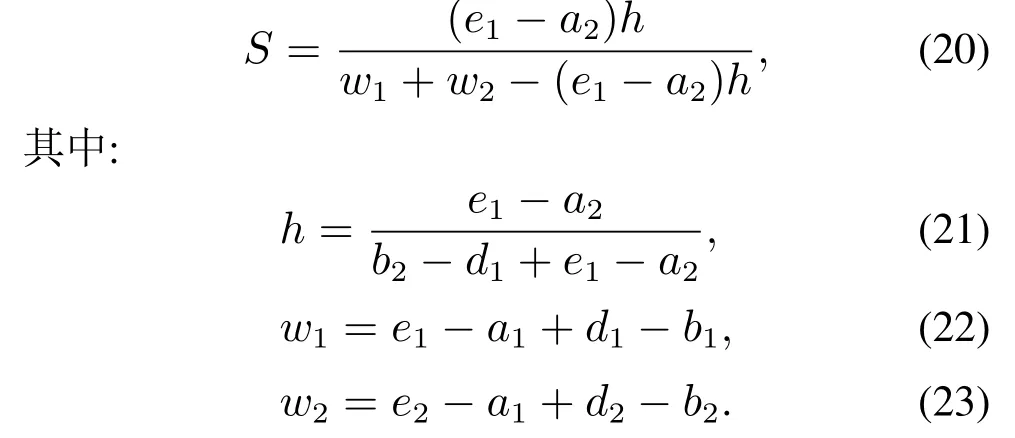
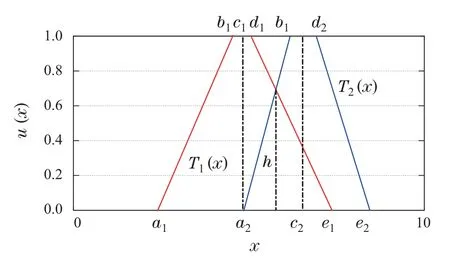
图4 情况2a下两个模糊集的相似度Fig.4 Similarity of two fuzzy sets for case 2a
情况2b如图5所示,两模糊集上下部分都有重合.两模糊集的相似度的计算方法如下:
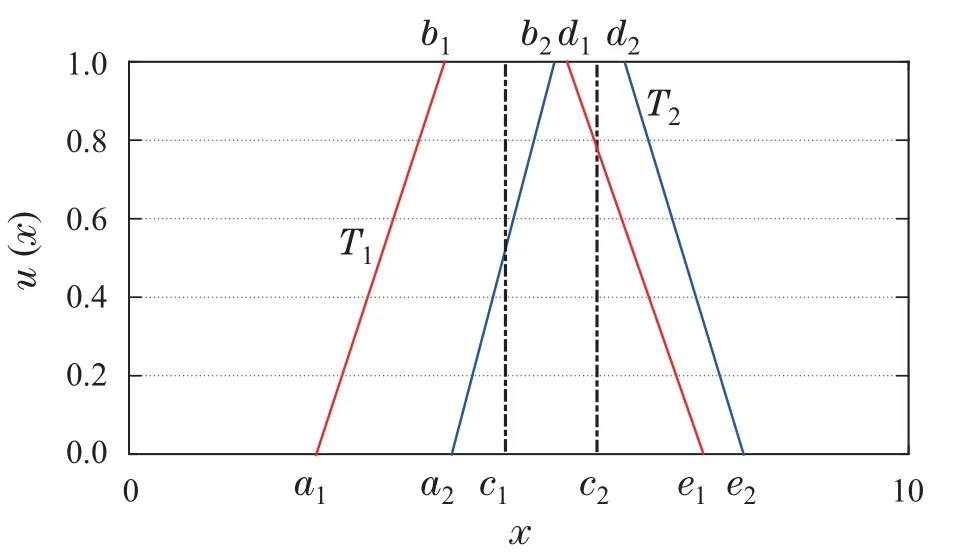
图5 情况2b下两个模糊集的相似度Fig.5 Similarity of two fuzzy sets for case 2b

情况3a如图6所示,相似度计算方法如下:

图6 情况3a下两个模糊集的相似度Fig.6 Similarity of two fuzzy sets for case 3a
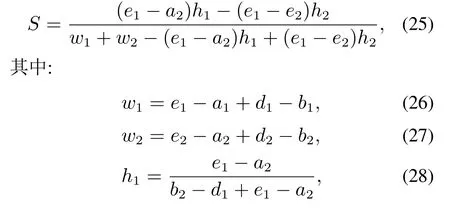

情况3b如图7所示,相似度计算方法如下:
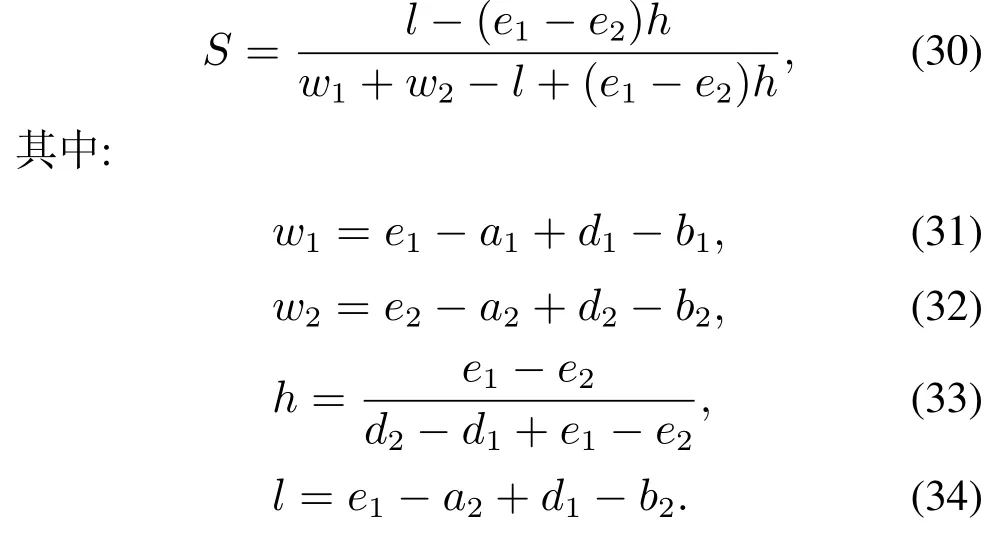
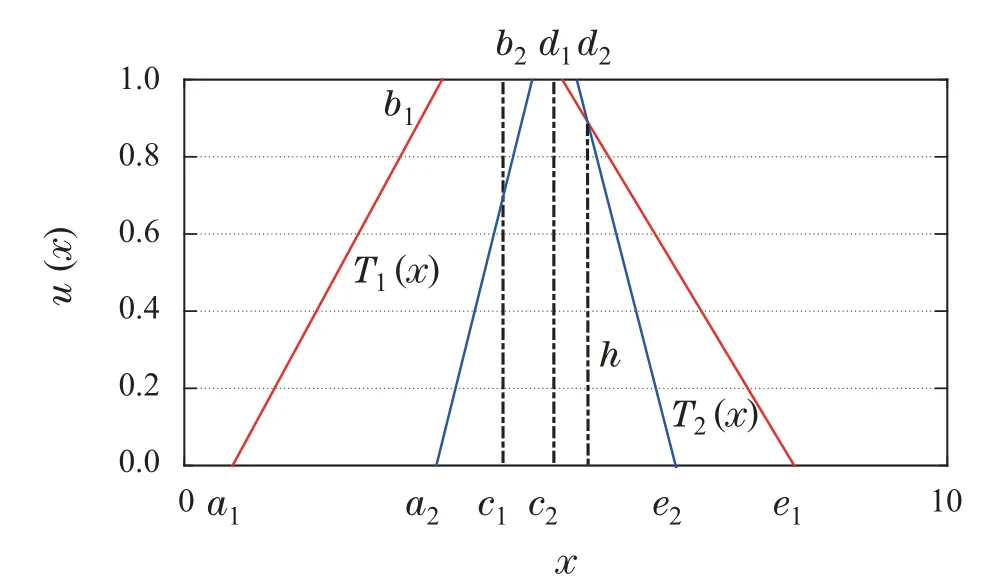
图7 情况3b下两个模糊集的相似度Fig.7 Similarity of two fuzzy sets for case 3b
此外,当模糊集的隶属函数无交集时,相似度为0.
3.3.2 T-S模糊系统简化
基于上述模糊集相似性度量方法,本节对T-S模糊系统进行模糊集剪枝和规则约简.
1) 模糊集剪枝.
模糊集剪枝包括两种情况:除去冗余模糊集和合并相似模糊集.
a) 除去冗余模糊集.
模糊集Xr,n,计算其与全集Un的相似性S(Xr,n,Un),其中,∨In ∈Un,In为第n个输入.若S(Xr,n,Un)>λr,则移除规则Rr的前件中的Xr,n.λr为移除冗余模糊集的阈值.
b) 合并相似模糊集.
若两模糊集的相似性S(T1,T2)>λm,则合并模糊集T1和T2为Tm.λm为合并相似模糊集的阈值.针对本文研究的高斯隶属函数的模糊集,T1和T2合并后的模糊集Tm对应高斯隶属函数的均值和方差为T1和T2对应高斯函数均值和方差取平均.
2) 规则约简.
规则约简包括规则删除和规则合并两种情况.
a) 规则删除.
b) 规则合并.
当两条模糊规则的前件十分相似但后件不同,可合并这两条规则.假设第r条规则对应的前件为Xr,1,Xr,2,···,Xr,N;第k条规则对应的前件为Xk,1,Xk,2,···,Xk,N.两条规则的相似度为

其中i=1,2,···,N.当S(Xr,Xk)超过阈值λc,所有的模糊集对均被认为相似,这两条规则可合并为一条规则.前件模糊集的合并方式与上述合并相似模糊集方法相同,而对应后件可取两条规则后件的均值

3.4 基于T-S模糊系统的预测控制器设计
基于第3.2节和第3.3节建模得到的T-S模糊系统,本节设计基于T-S模糊系统的SNN预测控制算法,算法框图如图8所示.
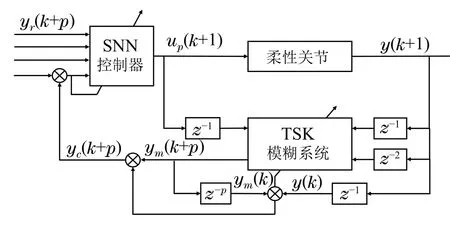
图8 基于T-S模糊系统的预测控制框图Fig.8 Block diagram of the predictive control based on T-S fuzzy system
定义SNN的输入到输出节点的权值系数为vi(k),输出层选择Sigmoid函数作为激活函数,Sigmoid函数具有指数形状,具有实现简单、导数容易获得、易于标准化等优点.SNN输出得到的控制信号可描述为
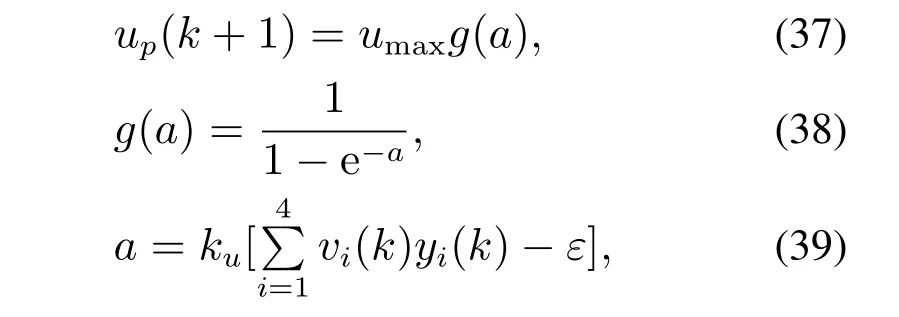
其中:ku为控制信号的放大系数,umax为控制信号的最大值,ε为设定的控制网络的阈值,g为Sigmoid函数.up(k+1)为SNN计算得到的控制信号.
T-S模糊系统通过当前时刻的控制信号,up(k+1)和前2个时刻的轨迹,y(k),y(k-1)预测被控对象第k+p时刻的状态,ym(k+p).根据单值预测的思想,控制信号每隔p步改变一次,因此加入矫正项,y(k)-ym(k)来补偿预测误差.第k+p时刻的预测输出为

SNN控制器的4个输入为
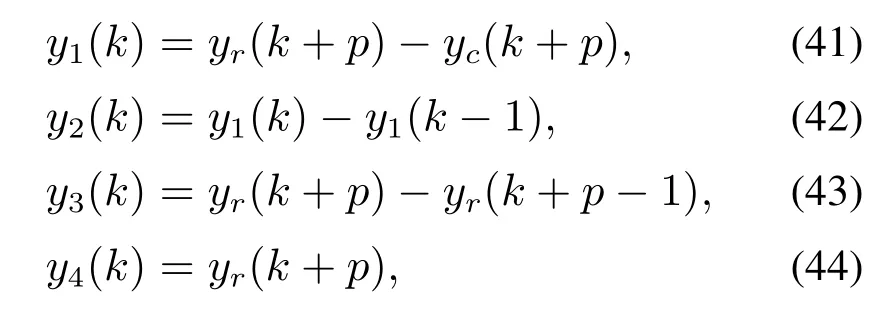
其中:yr(k)为k时刻的期望轨迹,y(k)为k时刻的实际轨迹.
设SNN控制器的性能指标函数为

根据式(2)-(6)可得
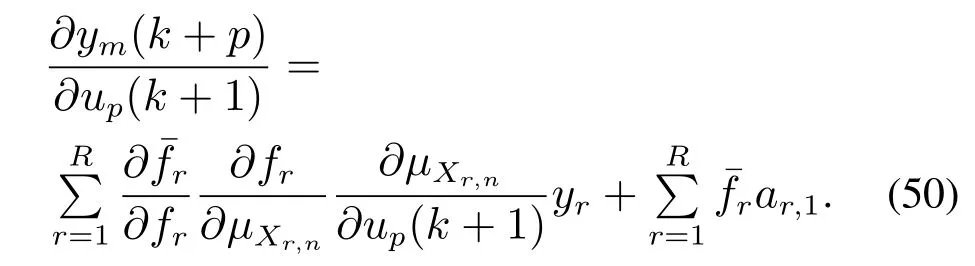
SNN控制器的权值系数可以通过以上方法进行在线更新,本文提出以下定理以保证参数更新过程中系统稳定.
定理1如果SNN控制器参数在线更新的学习率ηi满足以下不等式:
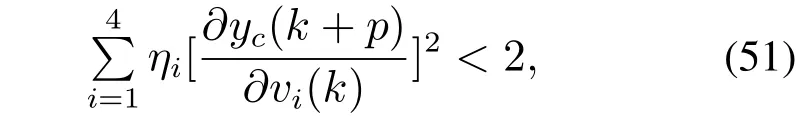
那么SNN控制器的学习过程可以收敛,系统渐近稳定.
证选择以下李雅普诺夫函数:
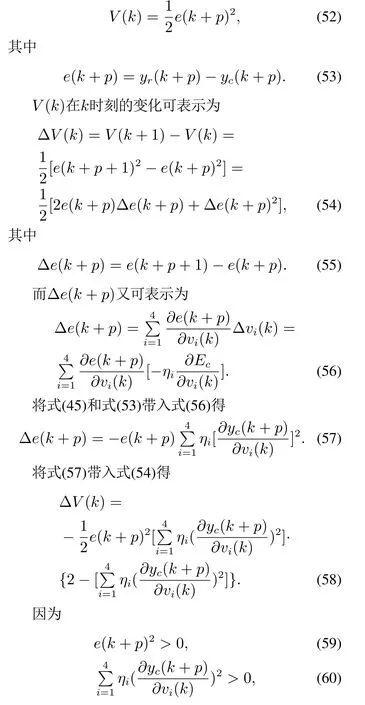
且根据式(51)可得

因此ΔV(k)<0.因此SNN参数更新过程整个系统渐近稳定,即当时间t →∞时,模糊系统的预测误差e(k+p)→0. 证毕.
此外,SNN的初始权值对控制性能有很大的影响,为进一步提升控制效果,考虑使用遗传算法对SNN的初始权值参数进行优化.
4 仿真与分析
本节根据式(1)所示的气动柔性关节动力学模型和相关参数,在MATLAB2013b/Simulink环境下对所提的控制方法进行验证和分析.仿真环境下优化得到的SNN初始权值和训练得到的T-S模糊模型将应用于后面的实物实验.
4.1 数据驱动的T-S模糊系统建模
首先,对气动柔性关节模型输入一个变频率的正弦控制信号驱动关节运动,采集运动数据,构建数据集.然后使用第3.2节所述数据驱动的建模算法对T-S模糊系统进行训练.该T-S模糊系统为3输入1输出,每个输入变量对应3个高斯隶属函数,因此一共27条模糊规则,每条规则对应后件如式(2)所示.
训练得到的T-S模糊系统的3输入对应的模糊集.而观察发现,输入3对应的模糊集T1和T2具有相似性,如图9所示.因此,根据前文所述的T-S模糊系统简化方法,模糊集T1和T2可合并为新的模糊集Tnew,输入变量3的模糊集数量减少为2.相应的,模糊集T1和T2对应的3·3·2=18条模糊规则可合并为9条,T-S模糊系统的规则总数由27简化为18.取对应后件参数的平均值作为合并后的后件参数.
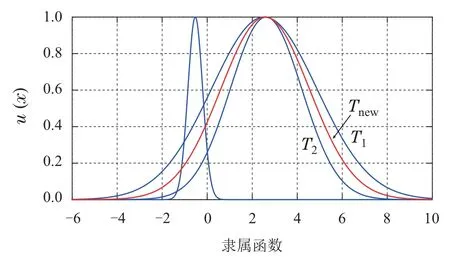
图9 输入变量3对应的模糊集Fig.9 Fuzzy sets of the input variable 3
为验证离线训练得到的T-S模糊系统预测的有效性,选用一个正弦控制信号驱动柔性关节运动,将相应信号输入T-S模糊系统,观察系统的预测输出曲线,此处预测范围p=3.此外,引入了一个3输入1输出的自适应神经模糊推理系统(adaptive network-based fuzzy inference system,ANFIS)作为对比.为了公平比较,ANFIS的隶属函数、后件和规则设置均与T-S模糊系统相同.使用MATLAB的ANFIS工具箱中的Hybrid方法对ANFIS系统进行训练,训练epoch数选择为3,训练的数据集与T-S模糊系统相同.
关节轨迹的预测结果如图10所示,预测误差如图11所示.由图10的预测结果可知,本文所提算法训练的T-S模糊系统及结构简化后的T-S模糊系统的预测轨迹与实际轨迹几乎重合,而ANFIS的预测输出与实际轨迹偏差较大.由图11可知,T-S模糊系统的最大预测误差小于0.2°,简化后的T-S模糊系统预测精度略有下降,最大误差为0.33°,而ANFIS系统的预测误差则超过10°,远大于T-S 模糊系统.因此,所提的数据驱动的T-S模糊系统可实现对被控对象动态特性的精准预测,而简化结构后的T-S模糊系统在模糊规则减少的情况下预测精度仅下降0.1°.
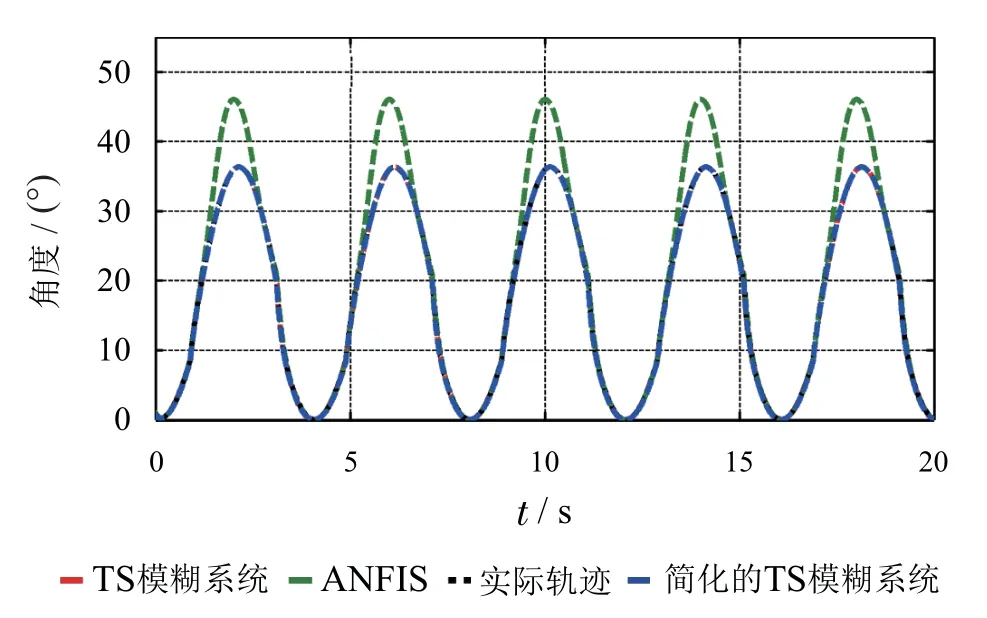
图10 预测轨迹曲线Fig.10 Trajectory prediction results
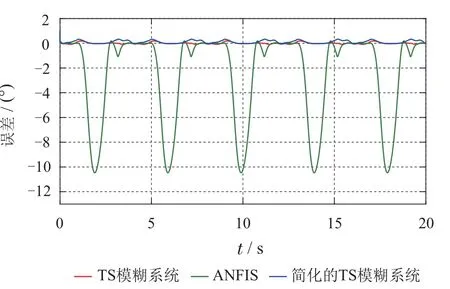
图11 预测误差对比Fig.11 Prediction errors comparison
4.2 SNN初始参数寻优
根据被控对象的动力学模型(1),使用遗传算法优化SNN控制器参数.优化前,采用试错法选择SNN控制器参数
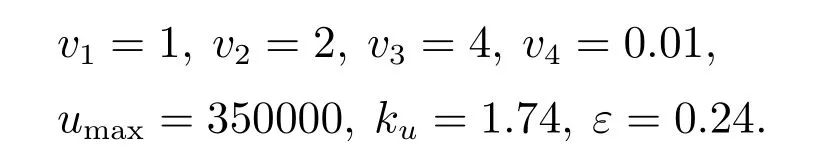
遗传算法中,每代个体数设置为20,总共进化代数为100,80%个体与适应度最高的个体交叉繁殖,10%个体发生变异.控制器参数的优化范围设置为

遗传算法优化后的SNN控制器参数为

图12和图13为遗传算法优化SNN初始参数前后轨迹跟踪结果对比,图中SNN-TS表示通过试错法设置初始参数的控制器,SNN-TS-GA表示通过遗传算法优化初始参数的控制器,SNN-SPTS-GA表示使用结构简化的T-S模糊系统的优化参数后的控制器.观察图12可发现,所有算法均可有效实现轨迹跟踪控制,但各算法跟踪轨迹与参考轨迹有不同程度的偏离.由图13可发现,对初始参数进行寻优后,算法SNN-TSGA和SNN-SPTS-GA的精度得到了明显提升,最大误差均低于1°,而SNN-TS的最大误差约为4°.可发现SNN-SPTS-GA的T-S模糊系统结构更加简单,算法的控制效果与简化前相近.此外,本文引入了滑模控制(sliding mode control,SMC)与文章所提方法进行比较.由图12和13可发现,SMC的跟踪轨迹在波谷附近与参考轨迹有一定的偏离,轨迹跟踪误差明显大于本文所提算法.而在实时控制中ANFIS系统体现出了较差的泛化能力,基于ANFIS的SNN预测控制器无法实现对柔性关节的轨迹跟踪控制.

图12 轨迹跟踪结果对比Fig.12 Comparison of the trajectory tracking results

图13 轨迹跟踪误差Fig.13 Trajectory tracking errors
5 实验与结果
5.1 平台介绍
气动柔性关节实验平台如图14所示,包括:气动肌肉、拉压力传感器、位移传感器、电磁比例阀和装有xPC系统工控机.空压机中的压缩空气经电磁比例阀控制,向气动肌肉系统提供气压,气动肌肉的随着充放气进行收缩拉伸运动,从而带动关节旋转.关节的角度数据通过的安装与转轴处的编码器实时获取后通过数据采集卡传入xPC系统目标机,目标机根据实时反馈的数据,通过宿主机传入的控制算法计算出实时控制信号.控制信号通过NI数据采集卡转化为模拟信号调节电磁比例阀的开度,从而控制气动肌肉内部气压,实现关节旋转角度的实时控制.

图14 气动柔性关节实验平台Fig.14 Experiment platform of the pneumatic flexible joint
5.2 实验结果与分析
本节通过实际实验验证所提的基于结构简化的T-S模糊系统的SNN预测控制器(SNN-SPTS-GA)的有效性.其中,T-S模糊系统通过MBGD-RDA算法经过离线训练和结构简化得到,SNN预测控制器的初始参数通过遗传算法优化确定.SNN控制器的初始参数为
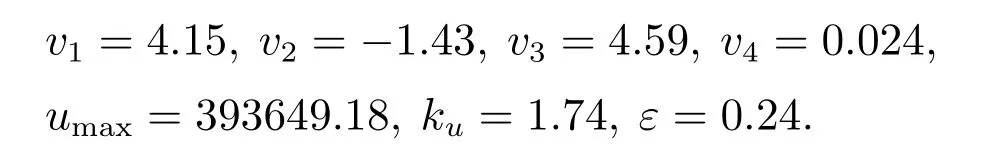
引入一个传统模糊控制器(fuzzy logic controller,FLC)作为对照,其输入为误差e和误差导数˙e,输出为控制信号变化率Δu,模糊规则设计与去模糊化方法与文献[19]相同.
图15为SNN-SPTS-GA和FLC轨迹跟踪曲线,可看出FLC的跟踪轨迹在峰值处偏离参考轨迹较多,而所提的SNN-SPTS-GA算法的轨迹与期望轨迹贴合更近.图16为对应的轨迹跟踪误差曲线,可发现,FLC的最大误差大于5°,而所提的SNN-SPTS-GA的最大跟踪误差在稳态时维持在3°以内.SMC作为典型的基于模型的控制算法,也与本文所提方法进行了比较.观察图15可发现,相比另外两算法,SMC的跟踪曲线与参考轨迹有较大偏离.而由图16可发现,SMC的跟踪误差远大于本文所提算法,其最大误差大于8°.因此,实验结果表明,所提的SNN-SPTS-GA算法相比传统的FLC和SMC跟踪精度有显著提升.
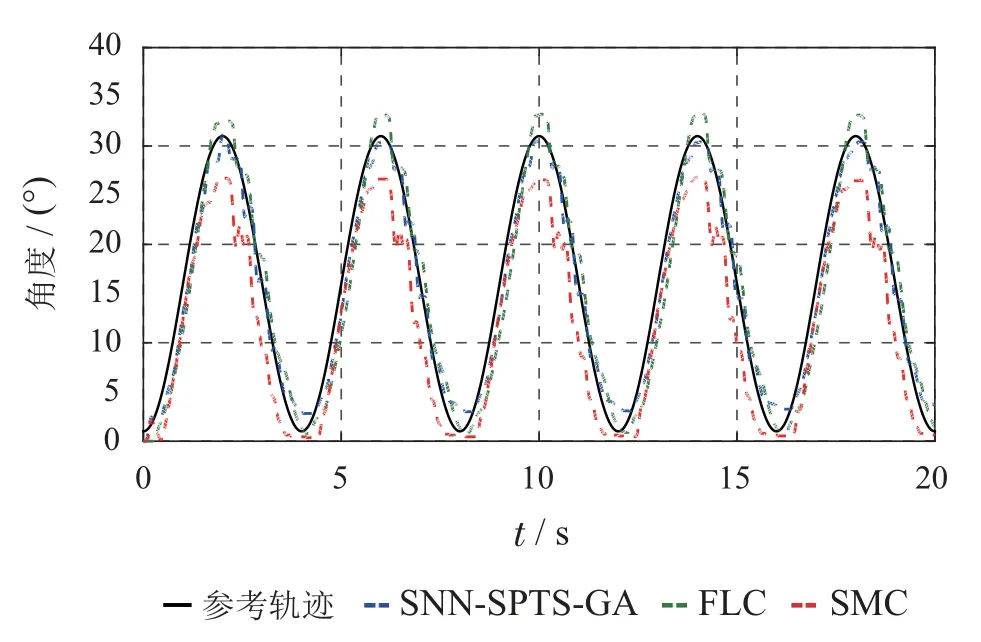
图15 轨迹跟踪曲线Fig.15 Tracking trajectories
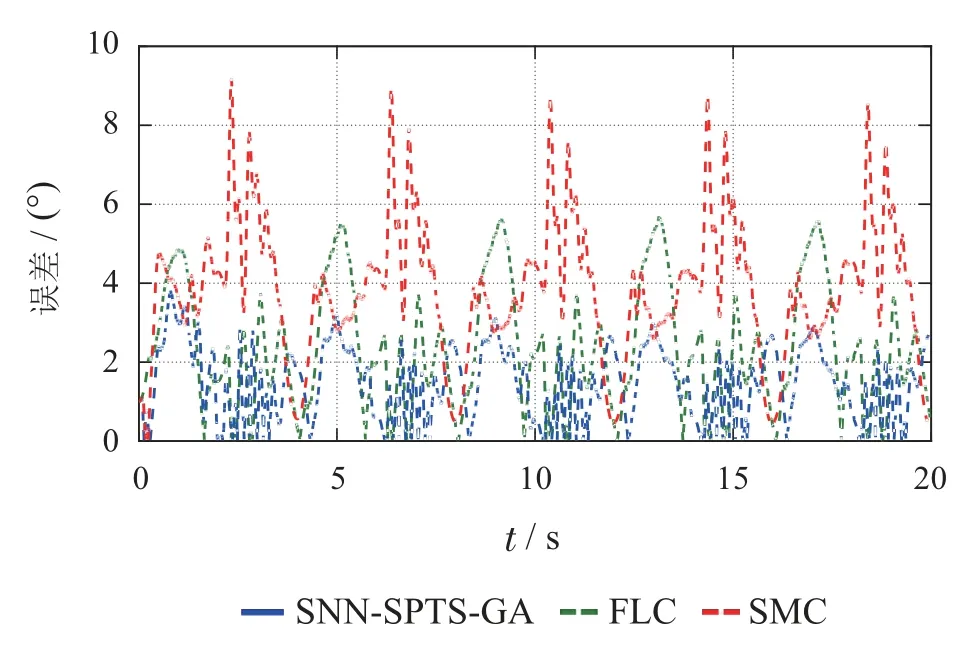
图16 轨迹跟踪误差Fig.16 Trajectory tracking errors
6 结论
本文针对气动柔性关节动态特性复杂、高精度控制困难的问题,设计了基于数据驱动的T-S模糊系统建模与预测控制算法.使用MBGD-RDA算法对T-S模糊系统进行离线训练,使其能够准确逼近被控对象的动态特性.设计了基于模糊集相似性度量的模糊系统简化方法,简化了T-S模糊系统结构.基于T-S模糊系统,设计了SNN预测控制器,并可在线更新SNN控制器参数.使用了遗传算法对SNN的初始权值进行了寻优.使用了梯度下降的方法在线优化T-S模糊系统参数.仿真和实验验证了所提算法的有效性.仿真结果表明,本文所提的基于数据驱动建模的T-S模糊系统在模糊规则数减少的情况下,仍能维持较高的预测精度,达到好的控制效果.实验结果表明,本文所提SNN-SPTS-GA预测控制器可实现对气动柔性关节的高精度轨迹跟踪控制,其控制效果优于传统的模糊逻辑控制器.
在算法上,笔者将研究预测准确度更高、结构更简单、泛化性能更好的模糊系统结构,提升控制器性能.在应用上,笔者将基于本文的方法,研究气动驱动的外骨骼机器人的控制问题,提升外骨骼控制效果.

