跳变约束下马尔可夫切换非线性系统滤波

杨衍婷 梁 彦

(1.咸阳师范学院数学与统计学院,陕西咸阳 712000;2.西北工业大学自动化学院,陕西西安 710072)

1 引言

在实际跟踪中,信息不仅可以来源于雷达、红外等骨干装备,还可以来源于飞行航路、道路等形成的等式不等式约束[1].例如,直升机受限于最大升限的高度约束和最远航程的距离约束,高超弹服从一定动力学约束,扩展目标服从目标几何关系约束,编队飞行服从队形几何限制约束,海航、民航、车辆服从一定航路,道路约束等.这些约束信息具有自己固有的存在形态且不受外界干扰从而有很大的利用价值.例如,在目标跟踪中,可以利用目标的最大最小速度限制提高跟踪精度.因此,充分挖掘系统特性和环境限制等带来的约束信息,可以使得动态系统面临的建模不确定在状态估计中得到一定程度的弱化,从而提高估计性能.通常地,约束可以分为两大类:等式约束和不等式约束.由于等式约束包含更精确的系统信息,因而在实际中可以明显改善滤波精度,所以,等式约束滤波问题的研究具有重要的理论价值和现实意义.

对于线性等式约束滤波,通常采用系统模型缩减法[2]、伪量测法[3]、以及投影法[4]这3种方法来实现.系统模型缩减法计算复杂度较低,可以实现最小均方误差估计,但是可能出现不同的消元产生不一样的估计结果以及消元过程失去物理意义等缺点[5].伪量测法不需专门设计滤波器,处理简单,但是会产生奇异的协方差矩阵从而带来数值不稳定问题[6].投影法将无约束状态估计投影到约束空间,所产生的估计结果不一定是最优的[4].对于非线性的等式约束,即使是线性系统也不一定能得到封闭形式解析最优解.非线性等式约束滤波的方法主要包括投影法[7]、伪量测法[8]、基于泰勒级数展开的近似[3]、基于确定性采样的无迹卡尔曼[8]、以及基于滑动水平估计的滤波方法[3]等.目前,线性等式约束滤波的研究已日趋成熟,非线性等式约束滤波研究取得了较大进展,但是非线性等式约束问题的本质挑战尚未解决:非线性等式约束通常需要近似,很难得到解析最优解,因为要考虑估计精度与计算量之间的折中,所以具体问题采用具体的算法,很难给出严格统一的滤波框架.实际中,往往出现非线性等式约束的情况.例如,在非合作机动目标跟踪中,目标的运动若直接用简单线性模型进行刻画,则非常不准确,如果想要获得满意的估计精度,需要对不确定系统进行非线性建模.因此,研究非线性等式约束下系统的滤波问题意义重大.

进一步地,在实际中,由于机动目标运动非合作性,无论是系统状态所受约束还是动态系统演化,都存在无法用单一模型刻画的情况.例如,在交叉道路机动目标跟踪中,一方面,感兴趣的目标在交叉道路上的机动运动很难用单一典型目标运动模式(诸如匀速直线,匀加速直线或转弯运动等)来进行有效建模;另一方面,对于被观测目标,由于可选择的运动道路的多样性,其实际的运动状态约束亦很难靠单一的约束直接进行描述.多模型估计[9-11]被认为是目标运动不确定性的主流机动目标跟踪方法.在多模型估计中,跳变马尔可夫过程是描述时变系统不确定模态的典型方法.跳变马尔可夫过程[12-13]通过不同时间段内不同系统的演化模式覆盖系统整个的演化过程.它重在有效刻画模型间的切换,认为相邻时刻不确定参数或模式往往服从一定的概率转移关系,更加符合机动目标跟踪等实际工程的应用,因而在目标跟踪[14-15]、信号处理[16]、过程控制[17]、故障检测与诊断[18]等领域得到广泛应用,相关离散时间跳变马尔可夫系统的状态估计问题受到了广泛关注.

针对上述跳变约束下马尔可夫切换非线性系统滤波问题,若直接采用伪量测法,将量测和约束扩维,则状态上存在一个马尔可夫链,量测上存在两个马尔可夫链,交互式多模型方法不能够直接使用.进一步地,跳变马尔可夫过程和系统的非线性耦合,在交互式多模型方法中如何得到快速高精度的估计结果是难点.Zhou[19-21]考虑了系统在不同模式下的切换,但这种切换不是依概率的,系统多个模式间的推进不服从跳变马尔可夫过程,并且在每个模式下,文献[19-21]的系统演化是线性的.Zhou[22-23]考虑了系统模型不确定下的状态估计问题,这种模型的不确定性综合了模式切换结果,与跳变马尔可夫过程有着本质的不同.此外,Zhou[19,21,23]将系统误差建模为外部扰动,针对系统模型不确定和外部扰动,设计了鲁棒滤波器.本文系统模型不确定是具有特定的马尔可夫切换性质的,系统误差是服从一定的统计规律的随机噪声,综上所述,文献[19-23]中的方法不适合本文所提问题的滤波器设计.因此,本文提出一种新的非线性约束滤波算法,主要创新点如下:针对状态切换与跳变约束共存,定义了新假设集,以包含双跳变马尔可夫参数可能取值,基于最优贝叶斯滤波,推导出状态与假设的后验概率递推更新;基于线性统计回归,利用伪量测法,给出了非线性系统滤波的近似解析最优解;最终给出所提算法的稀疏网格积分近似最优估计实现.

2 问题描述

考虑离散时间跳变马尔可夫约束非线性系统如下所示:

注1在实际中,存在系统状态所受约束和系统运动无法用单一模型刻画的情况.以机动目标跟踪为例,在交叉道路下,目标的机动运动很难用匀速直线,匀加速直线或匀速转弯运动等来进行有效建模.此外,由于道路交叉,目标的实际运动状态约束亦很难靠单一约束直接进行描述.

3 基于最优贝叶斯滤波状态后验概率递推

由于系统是涉及两个马尔可夫跳变参数的多模态,考虑多模态系统一种直接方法就是在每一时刻求取每个模态下的状态后验概率,之后进行输出综合.因此,依据跳变马尔可夫参数取值,假设

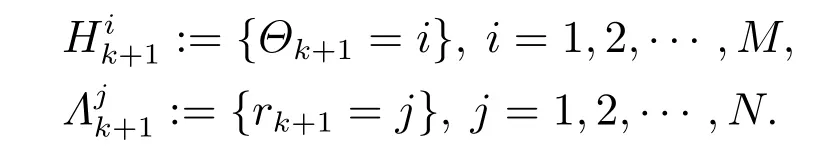
由于所考虑问题是非线性约束系统,对于非线性等式约束,一种直接的处理方法是考虑伪量测法.设zk是真实量测yk和约束扩维后形成的新的量测,则所考虑系统状态上存在一个马尔可夫链Θk,而量测上存在两个马尔可夫链Θk,rk,对于这样的系统的滤波问题,交互式多模型方法不能够直接使用,因此,需要探索新的方法完成系统的状态估计.

记Z1:k代表量测序列{z1,z2,···,zk}.根据最优贝叶斯滤波,有

定理1状态后验概率p(xk+1|Z1:k+1)递推如下:

4 基于统计线性回归的非线性系统滤波

由于系统非线性,这里,采用统计线性回归方法线性化非线性函数[24-25].统计线性回归线性化时考虑了先验随机变量的不确定性,因此,在统计意义上,所得到的线性化函数比简单使用一阶截断泰勒级数展开准确.

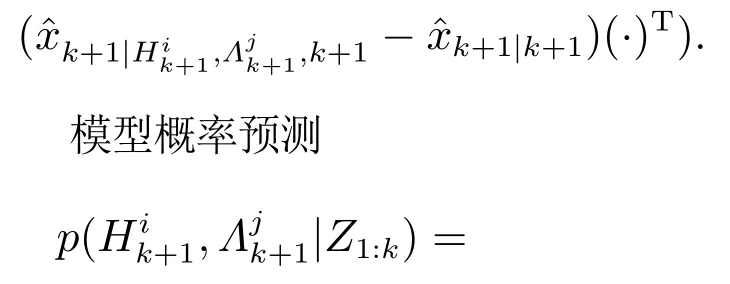
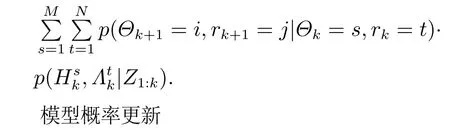
5 非线性系统滤波的稀疏网格积分实现

精度为3级时的稀疏网格积分精度达到了泰勒展开的5阶截断,优于无迹卡尔曼高斯函数泰勒3阶截断,同时计算量较小.无迹卡尔曼滤波器只是稀疏网格积分滤波器精度为2级时的一个特例.因此,本文采用文献[27]中的稀疏网格积分方法.精度级为3级时,根据矩匹配原则,可得nx维稀疏网格积分点和相应的权重如下:

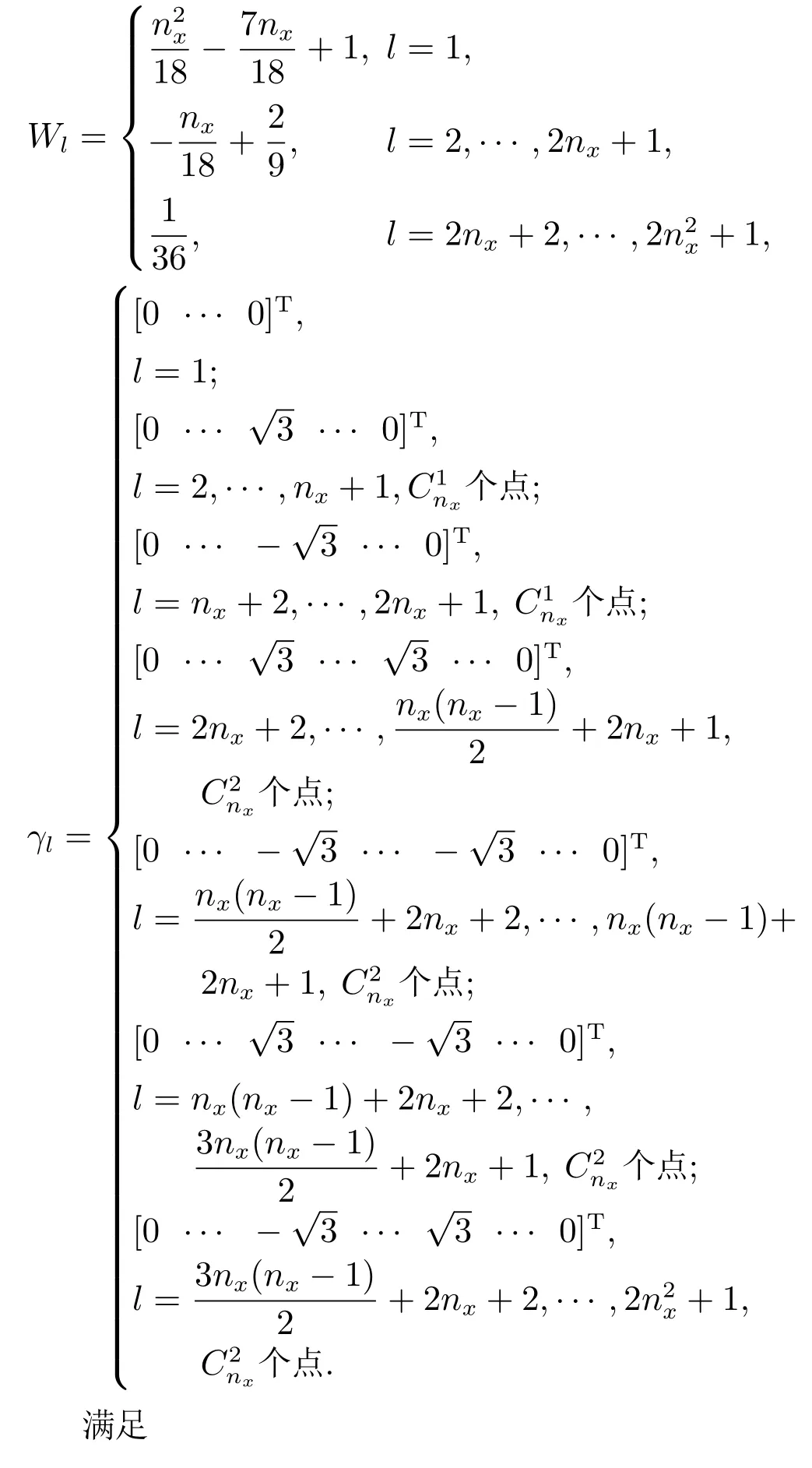
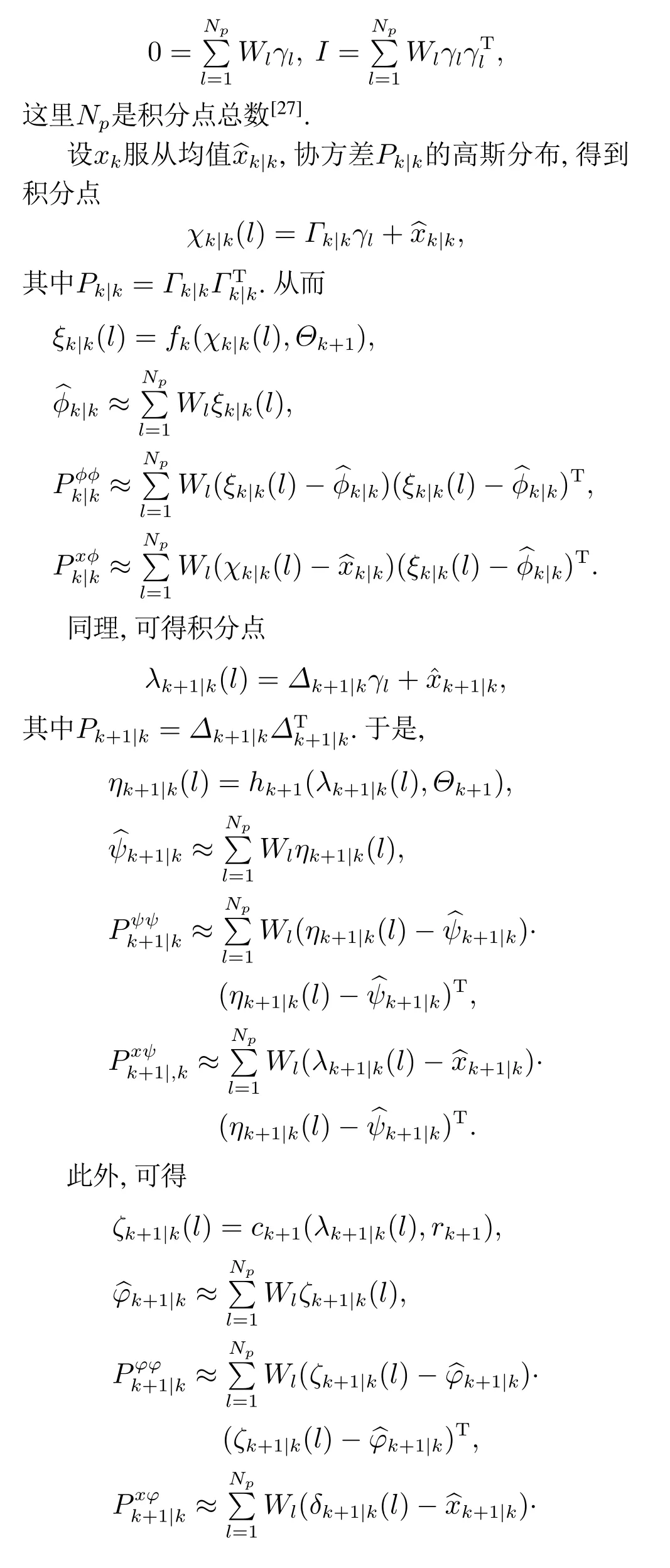
6 仿真验证

系统过程噪声协方差

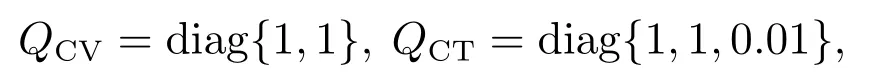
传感器采样周期为T=1 s.

在仿真场景中,目标共运行了100 s.在前25 s,目标做CV运动,在接下来的25 s,目标做CT运动,在随后的25 s,目标继续做CT运动,这时,速度放大1.5倍,最后的25 s,目标再一次回到CV运动上来.雷达量测

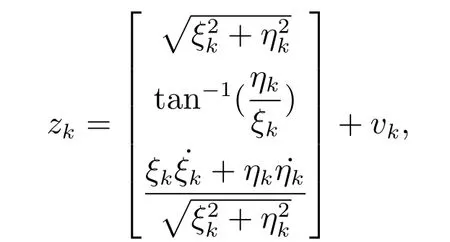
量测噪声协方差为Rk=diag{502,0.0012,25}.

在CV运动时,目标受限于直线约束

在CT运动时,从25到50个采样时刻,目标受限于小圆约束

在仿真中,产生量测数据时,采用投影法使目标运动满足约束.

目标的运动服从马尔可夫跳变过程,基于CV和CT两种模式,转移概率矩阵为

在仿真中,对于本文所提出的跳变约束非线性系统滤波算法,处理非线性函数时分别采用统计线性回归方法与泰勒展开方法(即基于统计线性回归的CMJF与基于泰勒展开式的CMJF),与传统的基于泰勒展开的交互式多模型算法,基于统计线性回归的交互式多模型算法(即基于泰勒展开式的IMM,基于统计线性回归的IMM)相比较,基于1000次蒙特卡洛仿真实现,4种算法的目标在ξ方向的均方根误差如图1所示,目标在η方向的均方根误差如图2所示,目标角速度估计和均方根误差如图3所示.从图中可以看出,无论位置,速度,角速度估计中,基于统计线性回归的CMJF算法优于其它3种算法.4种算法状态估计均方根误差均值如表1所示.

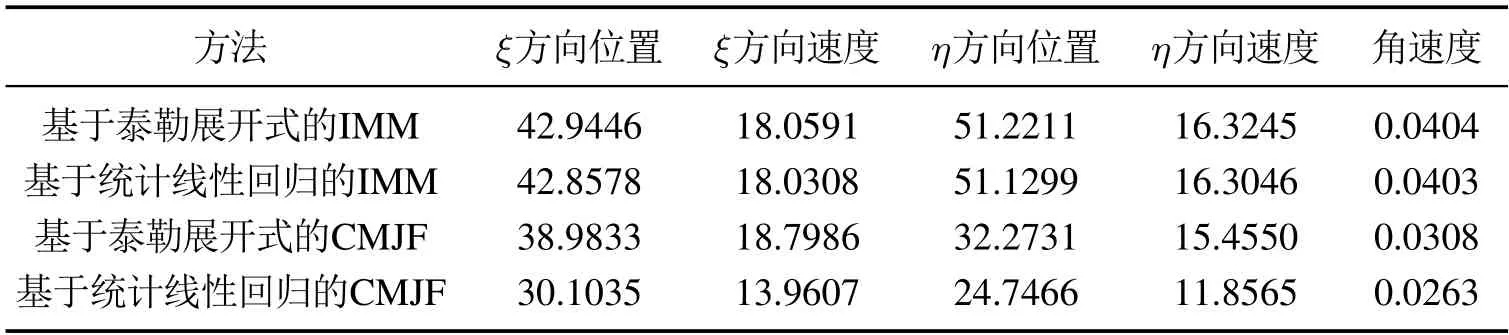
表1 4种算法的状态估计的均方根误差的均值Table 1 The mean of root mean square errors of state estimations for four algorithms

当系统过程噪声协方差增大到2.5倍时,4种算法的均方根误差如图4,图5所示,目标角速度估计和均方根误差如图6所示.4种算法均方根误差均值如表2所示.

表2 当系统过程噪声协方差增大时4种算法的状态估计的均方根误差的均值Table 2 The mean of root mean square errors of state estimations for four algorithms when the covariances of system process noises increase

从图1-6和表1-2中可以看出,系统过程噪声增大,约束起显著作用,利用约束可以提高系统状态的估计精度.在仿真中发现当系统非线性程度较强时基于泰勒展开的滤波算法容易发散,本文在仿真中剔除了误差较大的估计值.此外,从图1-2和图4-5可以看出,基于统计线性回归的CMJF算法降低了峰值误差,而对于目标跟踪而言,峰值误差的降低有着重要意义.峰值误差过大会导致后续数据关联失效从而导致航迹丢跟.

图1 目标在ξ方向的均方根误差Fig.1 Root mean square errors of the target in ξ

图2 目标在η方向的均方根误差Fig.2 Root mean square errors of the target in η

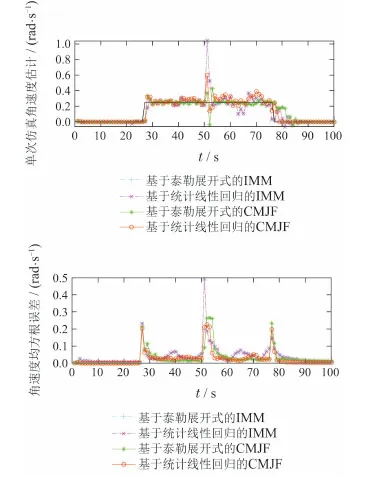
图3 目标角速度估计与均方根误差Fig.3 Angular velocity estimations and root mean square errors of the target

图4 过程噪声协方差增大时目标在ξ方向的均方根误差Fig.4 Root mean square errors of the target in ξ when the covariances of system process noises increase

图5 过程噪声协方差增大时目标在η方向的均方根误差Fig.5 Root mean square errors of the target in η when the covariances of system process noises increase

图6 过程噪声协方差增大时目标角速度估计与均方根误差Fig.6 Angular velocity estimations and root mean square errors of the target when the covariances of system process noises increase

基于统计线性回归的CMJF算法与比较算法的平均运行时间如图7所示,其中,仿真实现是在Intel(R)Core(TM)i5-4200M CPU@2.50 GHz 2.49 GHz的计算机上,利用MATLAB 2019a.同时,运行时间同时使用“tic”和“toc”函数度量.明显地,尽管基于统计线性回归的CMJF算法的平均运行时间稍微长于其他比较算法,然而它的运行时间很短,大约2.1×10−3s.这表明基于统计线性回归的CMJF算法的运行时间满足大多数工程实际的应用要求.

图7 平均运行时间比较Fig.7 Comparison of the average running time

基于统计线性回归的CMJF算法与比较算法在ξ方向,η方向的位置平均协方差如图8所示.从图8可以看出,基于统计线性回归的CMJF算法与比较算法在收敛速度上差不多,在10～20的采样时刻,基于统计线性回归的CMJF算法与比较算法均趋于收敛,其中,算法中尖峰的出现是由于目标机动造成的.

图8 平均协方差比较Fig.8 Comparison of the mean covariance

7 结论

本文利用线性统计回归线性化非线性函数,将线性化的约束扩维到真实量测中.在概率密度高斯假设下,推导出状态与假设概率后验估计递推更新,给出所提算法稀疏网格积分滤波实现.由于系统状态演化,量测和约束建模不局限于同一个马尔可夫切换过程,从而应用更加广泛.

附录A 定理1的证明

由全概率公式,状态xk+1的条件后验概率展开如下:

附录B 定理2的证明

根据定理1,基于卡尔曼滤波可得定理2的结论.