基于迭代学习和神经网络的船用起重机控制

林静正,方勇纯,卢 彪,郝运嵩,曹海昕

(南开大学人工智能学院机器人与信息自动化研究所,天津 300350)

1 引言

近些年,伴随着人类社会的高速繁荣,加大资源开采,扩张活动领域是必然的发展趋势.作为覆盖地球71%表面积的重要战略资源,海洋逐渐受到关注,海上作业活动也日益频繁,比如货物的吊运输送、设备的投放回收、船只间的补给等.在这些作业任务中,船用起重机扮演着不可或缺的角色.因此,对其展开研究具有非常重要的实际意义和广阔的应用前景.

与陆上起重机类似,船用起重机是一种典型的欠驱动系统.目前,对陆上起重机系统的研究已取得较大的进展:国内外学者基于输入整形[1]、滑模控制[2]、自适应控制[3]、预测控制[4]等理论提出了多种控制器设计思路.然而,对船用起重机控制的研究还未成熟,仍面临着许多难题.首先,船用起重机系统内部存在摩擦力,未建模动态,参数不确定等干扰,使得基于模型设计的控制器难以保证在实际应用中达到预期的精度;更为重要的是,船用起重机需要在恶劣的海洋环境中进行作业,不可避免地会受到海浪、大风这类未知外部干扰的影响,使负载的定位精度下降,摆动加剧,给控制器的设计带来了极大的挑战.

为了解决上述问题,国内外学者陆续投入到对船用起重机的研究中来.在文献[5]中,Fang等人利用欧拉-拉格朗日法对船用起重机进行了建模,并设计了非线性控制器使状态变量较好地跟踪参考轨迹.在此基础上,Lu等[6]通过状态变量转换,将船体运动引起的动力学方程与起重机自身动力学方程结合,简化了控制器的设计.在文献[7]中,Hong等讨论了在海面较平稳时海浪对船用起重机状态的影响.一些学者基于滑模控制理论[8],模糊控制理论[9],神经网络算法[10]设计控制器来完成控制任务.Küchler等[11]通过预测海浪来进行补偿,同样对海浪特性进行研究的还有文献[12],然而,他们只关注了海浪的周期性质,并没有充分考虑海浪的非周期部分,在真实环境下效果可能无法到达预期.此外,许多控制器都假设所建模型是完全准确的,在控制器中包含大量的系统参数.而在很多应用场景下无法获得精确的参数信息,因此会大大降低控制效果[13].

根据上述分析,本文提出了一种基于迭代学习和神经网络的控制方法,通过补偿未知干扰,使起重臂和绳长到达期望位置,同时抑制负载摆动.本文首先将船用起重机动力学模型拆分为有驱和无驱部分以便后续控制器设计;接着通过周期估计器估计未知周期,并经过迭代学习补偿未知周期干扰;之后利用双层神经网络对非周期干扰进行估计补偿;在对未知干扰进行补偿后,基于反馈线性化设计控制输入.通过Lyapunov分析方法证明了期望平衡点是全局有界的.最后在所搭建的模拟船用起重机实验平台上进行了大量实验,充分验证了所设计控制器的有效性和鲁棒性.本文的主要贡献为

1) 提出了一种基于迭代学习和神经网络的控制方法.在有持续未知干扰的情况下,可以从理论上保证系统状态的全局一致有界性.

2) 对船用起重机系统受到的未知干扰进行了充分的考虑,将其拆分成周期与非周期两部分,利用迭代学习和神经网络分别进行补偿.使系统对干扰的估计更加准确完备,增强了控制器的鲁棒性.

3) 基于Stewart平台搭建了船用起重机实验系统,可以真实地模拟船用起重机工作环境.通过设计大量实验,充分验证了在恶劣环境下所提控制器的有效性.

本文其他部分安排如下:第2节对海浪干扰和船用起重机系统进行了建模分析,并描述了控制目标;第3节分别对周期和非周期干扰进行估计补偿,并利用反馈线性化设计了一种基于迭代学习和神经网络的控制器;第4节通过Lyapunov方法进行了稳定性分析;第5节展示了在模拟船吊平台上的实验结果;最后,在第6节对本文工作做了总结与展望.

2 问题描述

本节分析了船用起重机受到的干扰,将未知干扰分为周期与非周期干扰.基于此给出了船用起重机在未知干扰下的动力学模型,并描述了具体的控制目标.

2.1 干扰分析

船用起重机系统受到的干扰主要由海浪引起.通常将这类海浪干扰dp视为由N个具有不同幅值、周期以及相位的正弦函数叠加的形式[11-12]:

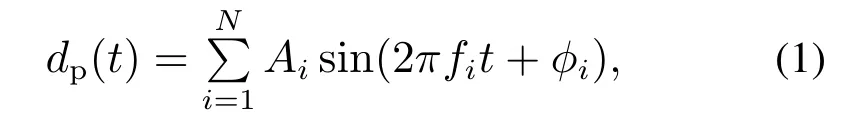
其中:Ai,fi,φi分别代表第i个正弦函数的幅值、频率和相位.定义T为的最小公倍数,则式(1)中的干扰具有周期性:

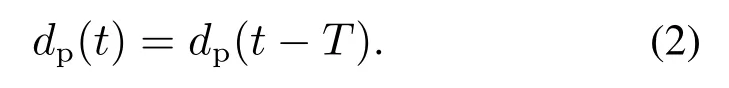
本文将这部分干扰视为周期性的,且结构和参数未知的一种干扰.需要说明的是,出于安全考虑,在海况极其恶劣的情况下,船只停止作业.因此本文考虑的船用起重机工作时所受海浪干扰有界,作如下合理假设.

假设1未知周期干扰具有已知上界Md,其周期T未知,但同样具有已知上界TM[15-16].

当海况平稳时,海浪可看作是若干正弦波叠加的模型,但当海面有风浪时,干扰会体现出非周期性质[17].并且,系统内部存在各种摩擦力、参数不确定等未知干扰.因此,在对船用起重机所受干扰做了详细考虑分析后,本文将未知干扰分为周期未知干扰与非周期未知干扰两部分,分别进行估计补偿.

2.2 系统模型及变换

图1是船用起重机的示意图,由船体、起重臂、吊绳、负载组成.Ts={Os,xs,ys,zs}表示动坐标系,Te={Oe,xe,ye,ze}表示大地坐标系.由海浪引起的船体俯仰运动以及升沉运动分别为α(t),h(t).基于欧拉-拉格朗日方程可以得到如下的动力学模型[14]:

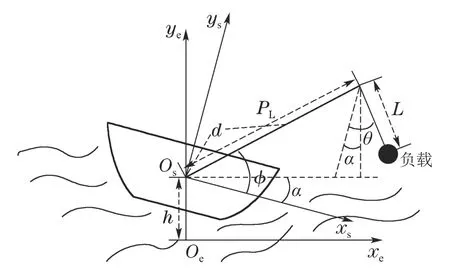
图1 船用起重机示意图Fig.1 Schematic model of the offshore boom crane

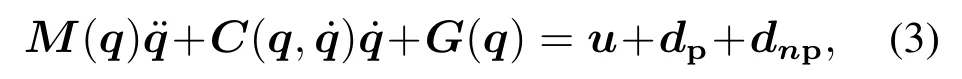
其中:

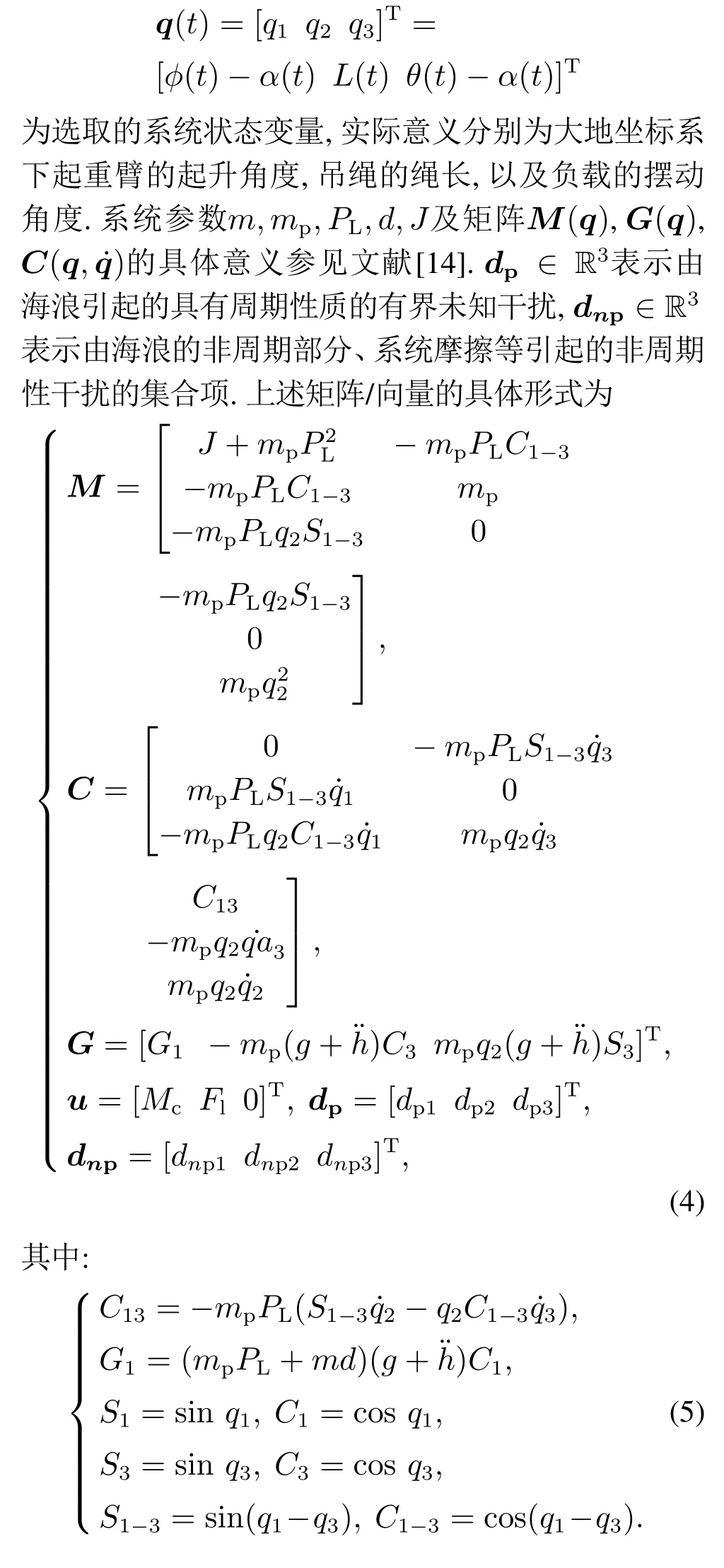
为了便于随后的分析,把式(3)拓展为以下形式:

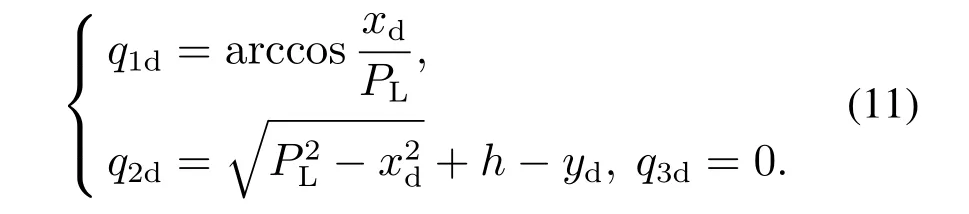
3 干扰补偿和控制器设计

本节中,首先设计了周期估计器对未知周期进行预测,并通过迭代学习控制补偿未知周期干扰;接着设计了双层神经网络以及权重更新律,来补偿未知非周期干扰;最后基于反馈线性化设计控制器.

3.1 周期估计器

3.2 周期干扰估计

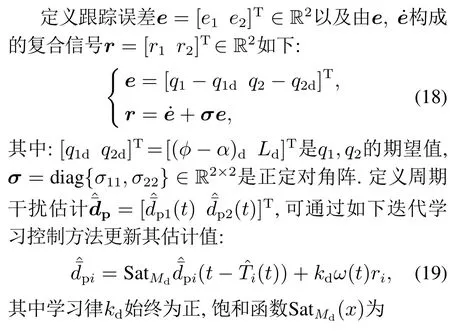
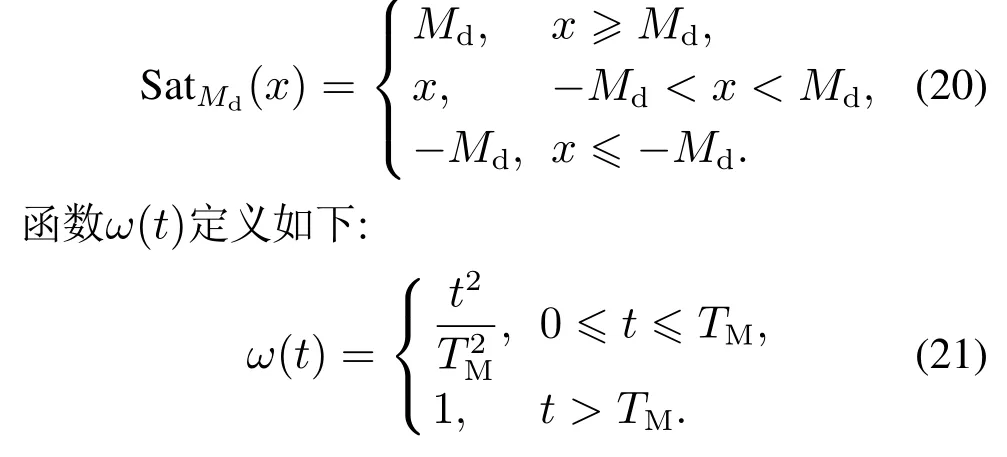
3.3 非周期干扰估计

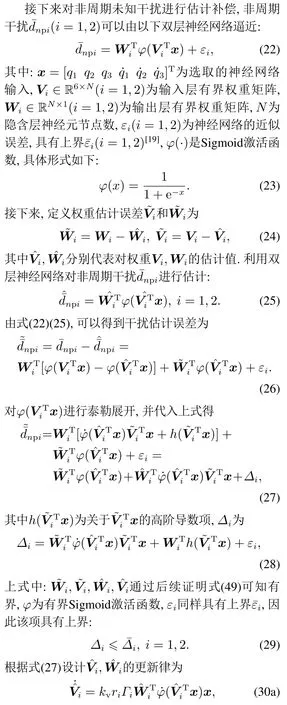
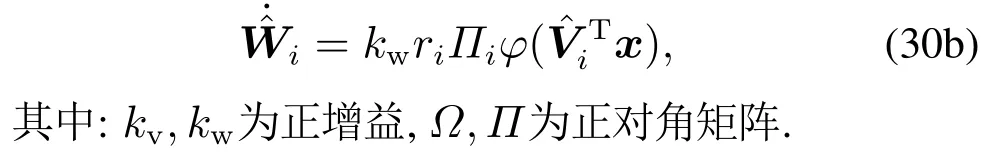
3.4 控制器设计

本小节在上述对未知干扰估计结果的基础上进行控制器的设计.对式(18)中的r求导并代入式(10)中:

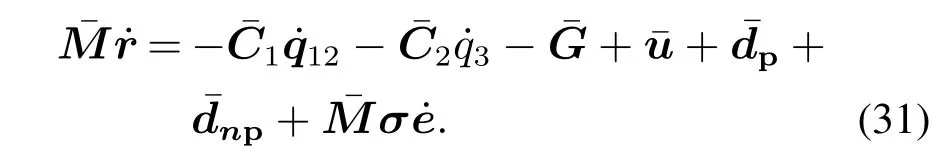
根据式(16)(19)(25)(30),设计神经网络与迭代学习控制相结合的反馈控制器:

4 稳定性分析

本节将对闭环系统期望平衡点的稳定性进行分析.

定理1对于受到海浪等未知干扰的欠驱动船用起重机系统(10),通过所设计的迭代学习更新律(16)(19)以及神经网络权重更新律(30),能够对未知干扰进行有效估计和补偿.在此基础上,提出的控制器(32)能够保证在有持续未知干扰的情况下,使起重臂以及绳长跟踪误差渐近收敛,负载摆角全局有界:

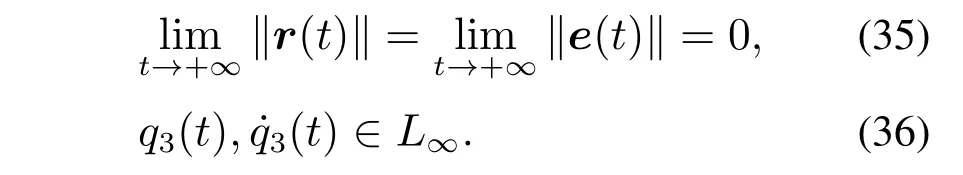
为了证明定理1,设计如下李雅普诺夫候选函数:

广东省9家“三甲”医院药师对互联网药事服务认知情况的调查分析 ……………………………………… 汪小惠等（2）：159

其中:第1项积分项是为了解决迭代学习的学习误差,第2项为误差信号相关项,后两项是为了解决神经网络权重的估计误差所设计.对式(37)求导,并代入学习律(19)-(21)(30)以及闭环系统方程(34),化简可得

至此,根据式(52)(54),可以得出结论:在有持续未知干扰的情况下,起重臂q1(t)和绳长q2(t)渐近收敛,负载摆角q3(t)全局有界.对定理1的证明结束.

5 实验结果

本节通过在模拟船吊实验平台上进行实验,对所提出的方法进行了验证.所搭建的实验平台如图2所示.一个缩小比例的悬臂起重机安装在一个Stewart六自由度平台上,该平台能够提供所需要的俯仰、升沉运动来模拟船用起重机的工作环境.悬臂和吊绳分别由两个带有编码器的伺服电机驱动,提供力/力矩的同时实时读回幅角φ(t)与绳长L(t).另外,在悬臂顶端安装有一个编码器用来测量摆角θ(t).为了保证控制的实时性,控制周期设定为10 ms.

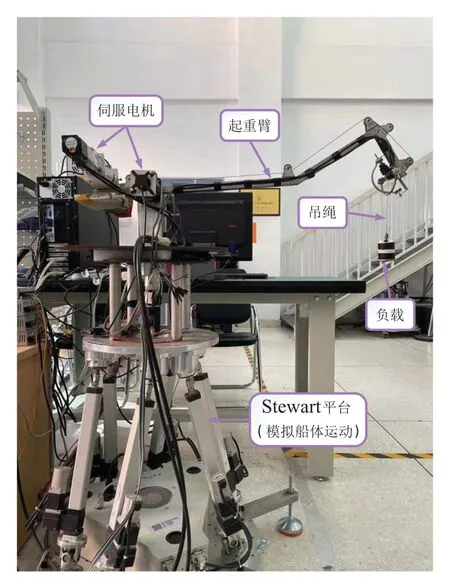
图2 船用起重机实验平台Fig.2 Experimental testbed

实验平台的各项参数如下:

所设计的控制器的各项控制参数如下:

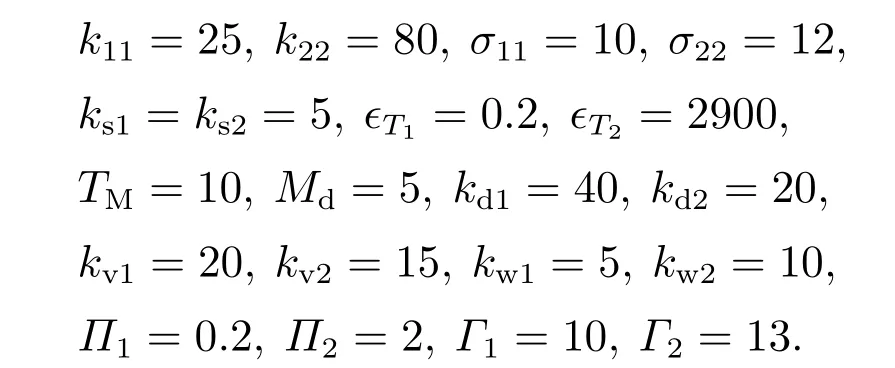
神经网络节点数为N=1,周期初值以及神经网络各权值初值设为

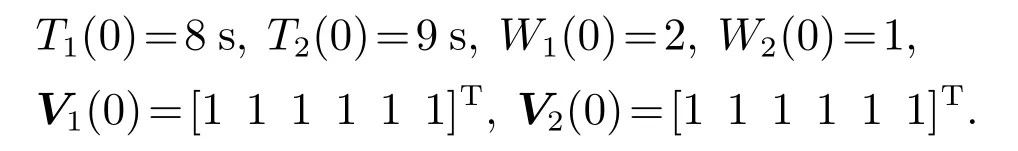
为了证明所提方法的优势,本节分为两个子小节.在第1小节的实验中,将本文设计的方法与其他方法在相同条件下进行对比;在第2小节中,对所提方法加入各类干扰来验证鲁棒性.

5.1 与其他方法进行对比

本节将所设计的控制器与线性二次型控制器(linear quadratic regulator,LQR)和文献[20]提出的自适应增益滑模控制器(以下用SMC表示)进行对比.将式(3)进行适当线性化后,设计Q矩阵为

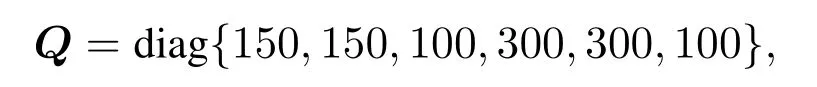
R为矩阵,R=diag{1,1},利用MATLAB工具箱求解里卡蒂微分方程,得到控制器输入

SMC控制器控制参数设计为k11=k21=20,k12=k22=5,γ1=γ2=3,λ1=λ2=0.1.

为了方便控制器之间的比较,定义如下性能指标:1)q3max:最大负载摆角的绝对值;2)q3var:负载摆角的方差;3)tq1:悬臂到达稳定的时间;4)tq2:绳长到达稳定的时间;5)xmean:x与xd之差的平方的平均数;6)ymean:y与yd之差的平方的平均数.

实验结果如图3-4和表1所示.从图3中可以看到,在有持续未知扰动的情况下,本文方法具有更好的控制效果.具体而言,本文方法控制起重臂和绳长到达期望位置所需时间更短;而对比方法到达期望位置所需时间较长,并且在期望位置附近有较明显的振荡.同时,本文所提方法能够更好地抑制负载摆角,而对比方法由于不能很好地补偿船体引起的干扰,表现出负载在期望位置附近来回摇摆,各项性能指标均劣于所提方法(具体指标见表1).因此证明了本文方法对未知干扰进行估计和补偿的有效性,更适用于实际船用起重机作业场景.

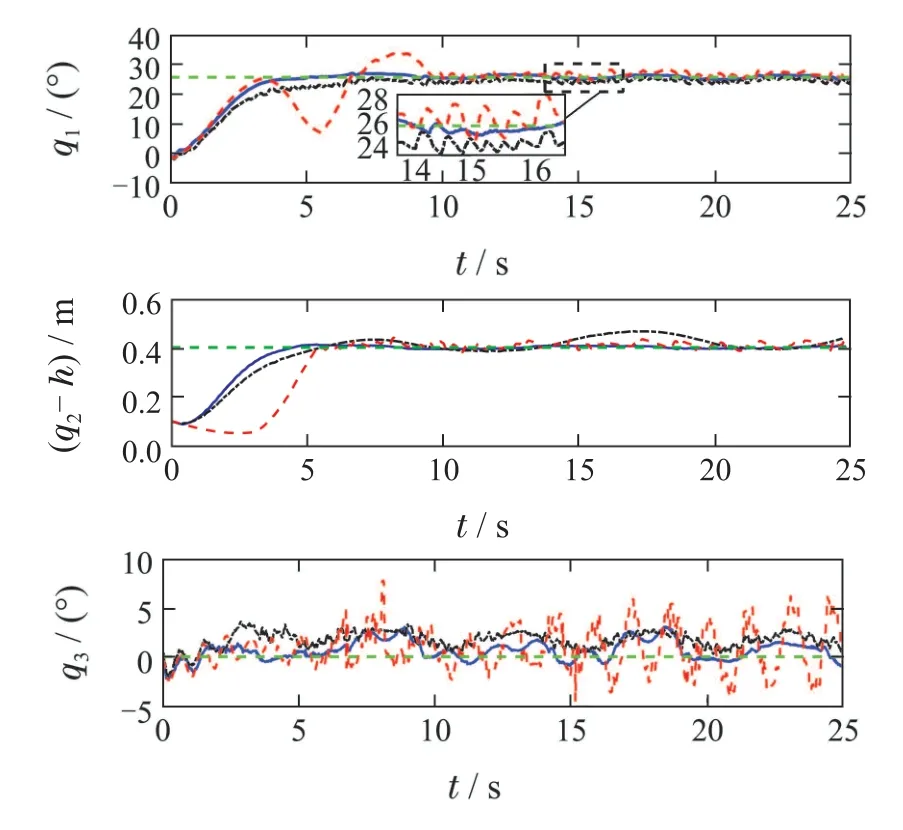
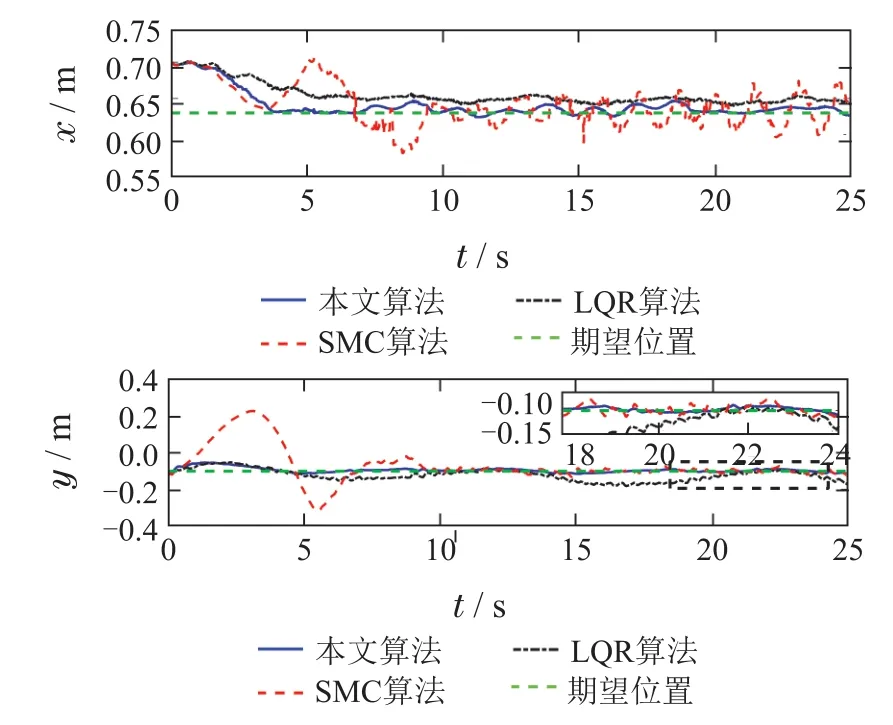
图3 本文设计方法,LQR方法,SMC方法[20]的实验结果Fig.3 Experimental results of the proposed method,LQR method,and the SMC method[20]

表1 各类方法的性能指标Table 1 Performance indices of different methods

图4的前两张图表示伺服电机的输出力/力矩.可以看到,本文方法的输出变化更平缓,峰值更小,而对比方法抖振明显,增加了安全隐患.图4剩余部分为对周期的估计,对周期干扰以及非周期干扰的补偿结果.在实验中给定俯仰和升沉运动的周期分别为5 s,10 s.结果证明了本文方法能够快速准确地估计干扰周期.

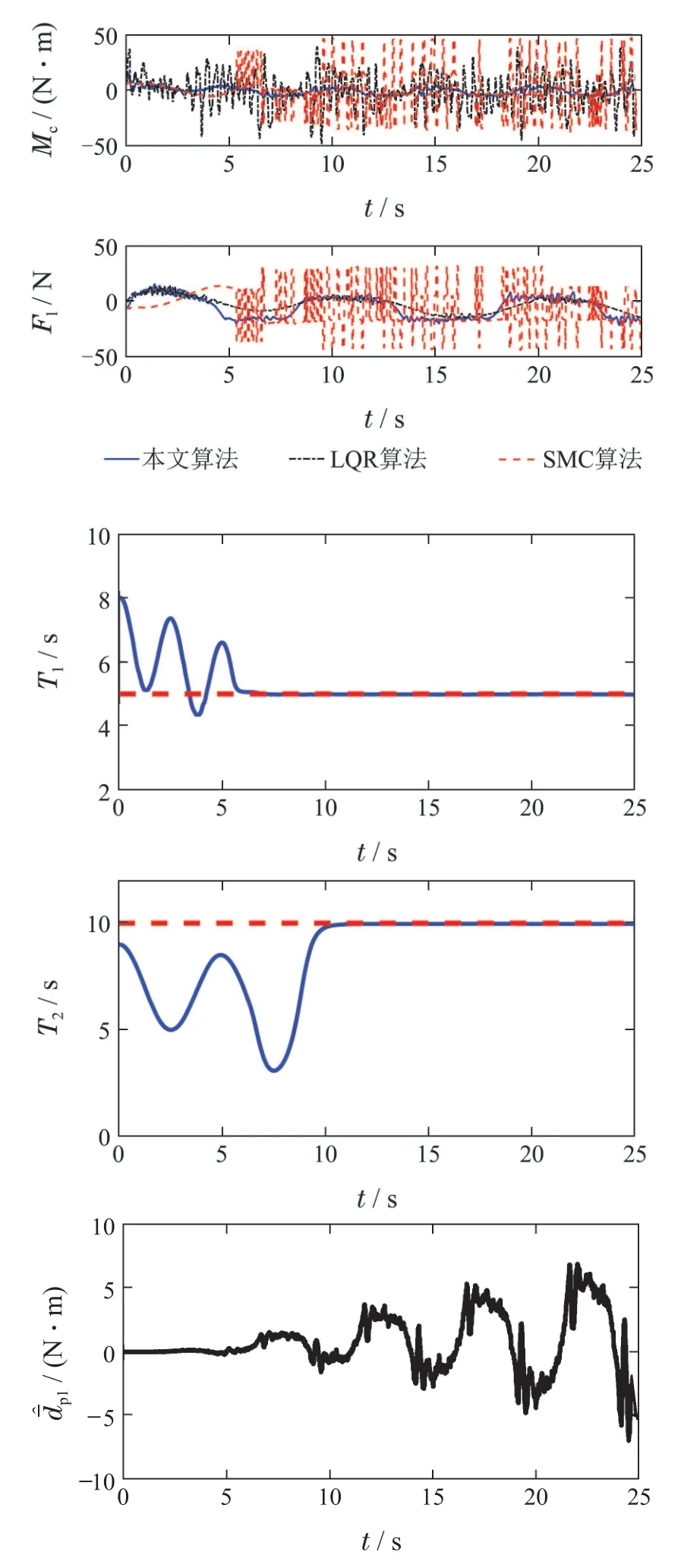
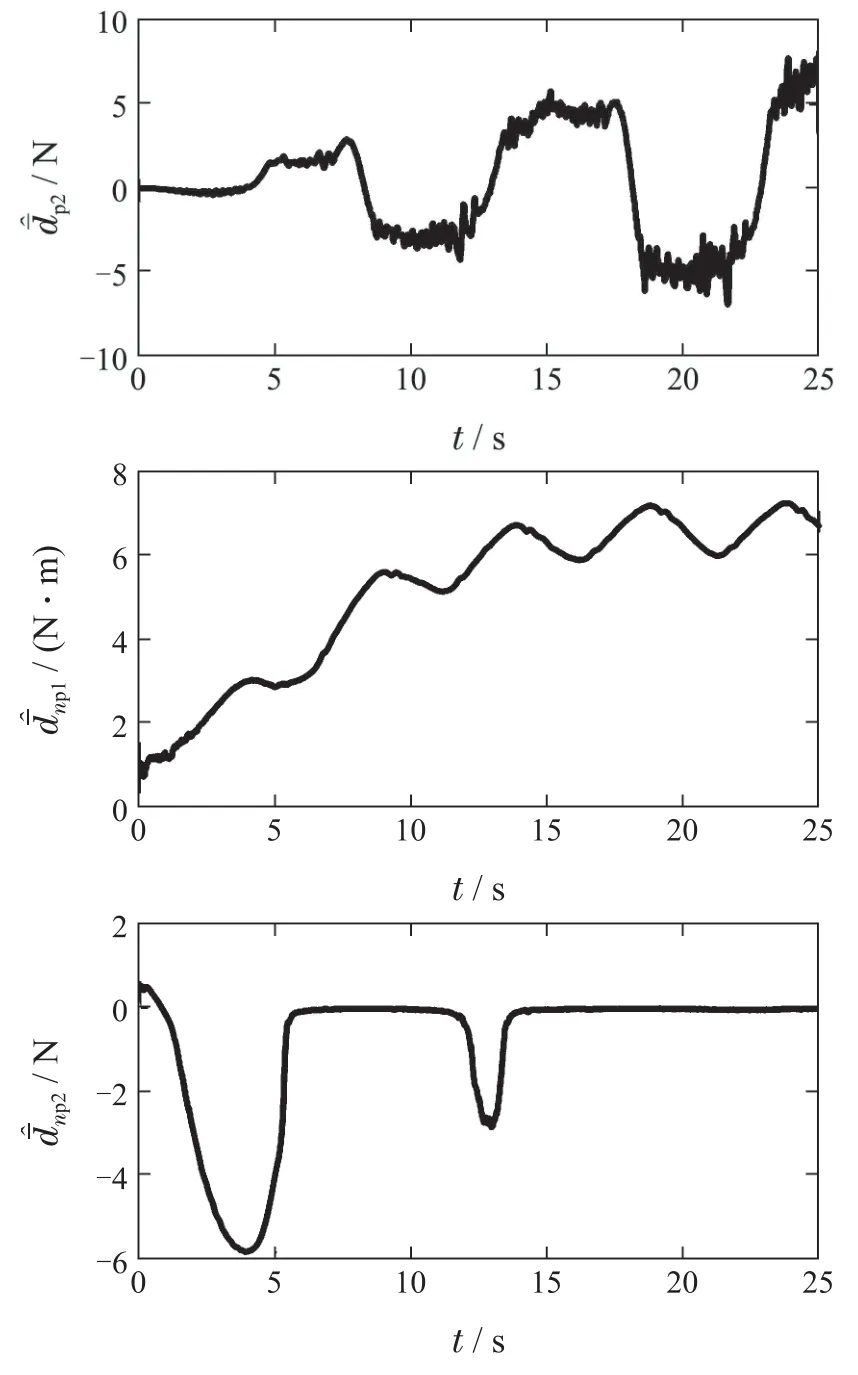
图4 本文设计算法,LQR算法,SMC算法[20]的实验结果Fig.4 Experimental results of the proposed method,LQR method,and the SMC method[20]

5.2 鲁棒性验证

为了验证本文控制器的鲁棒性,设计了两组实验.

实验1在时间t=20 s时将俯仰运动与升沉运动的干扰改变为

结果如图5-6所示.从图5可以看到,当干扰的周期以及幅值在控制过程中发生改变时,本文方法仍有很好的控制效果,负载的摆动始终控制在3°以内,且能够实现负载的定位.从图6中可以看到,在t=20 s时干扰α(t)和h(t)的幅值和周期都发生了变化,周期估计器可以很好地跟踪并且估计出干扰的周期,进而对干扰进行补偿,图中也很好地说明了干扰的周期与周期估计器得到的周期是一致的.证明了该方法对干扰的变化有较好的鲁棒性,在实际应用中具有重要意义.

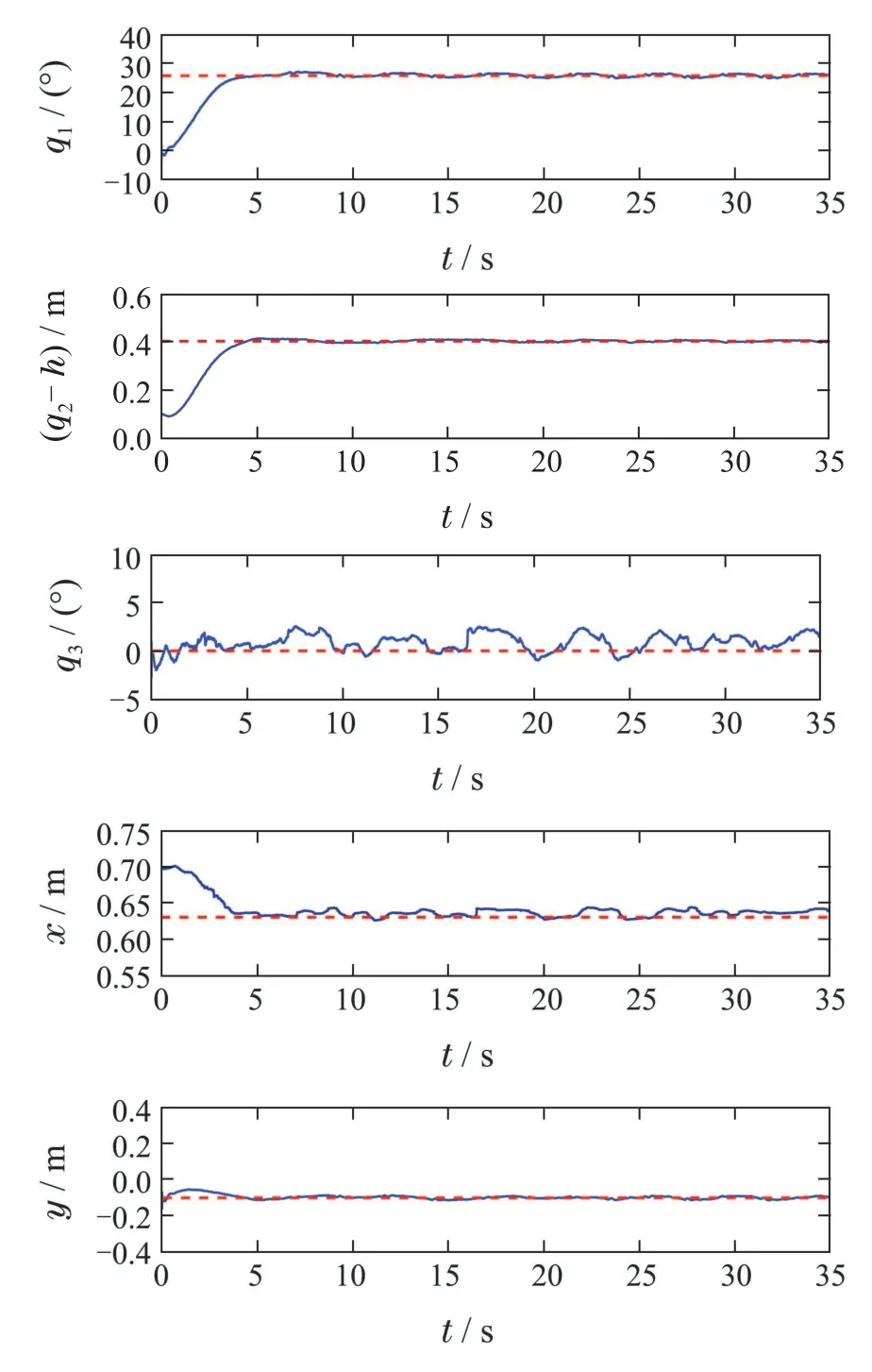
图5 干扰周期改变情况下的实验结果Fig.5 Experimental results under the condition of changing disturbance period

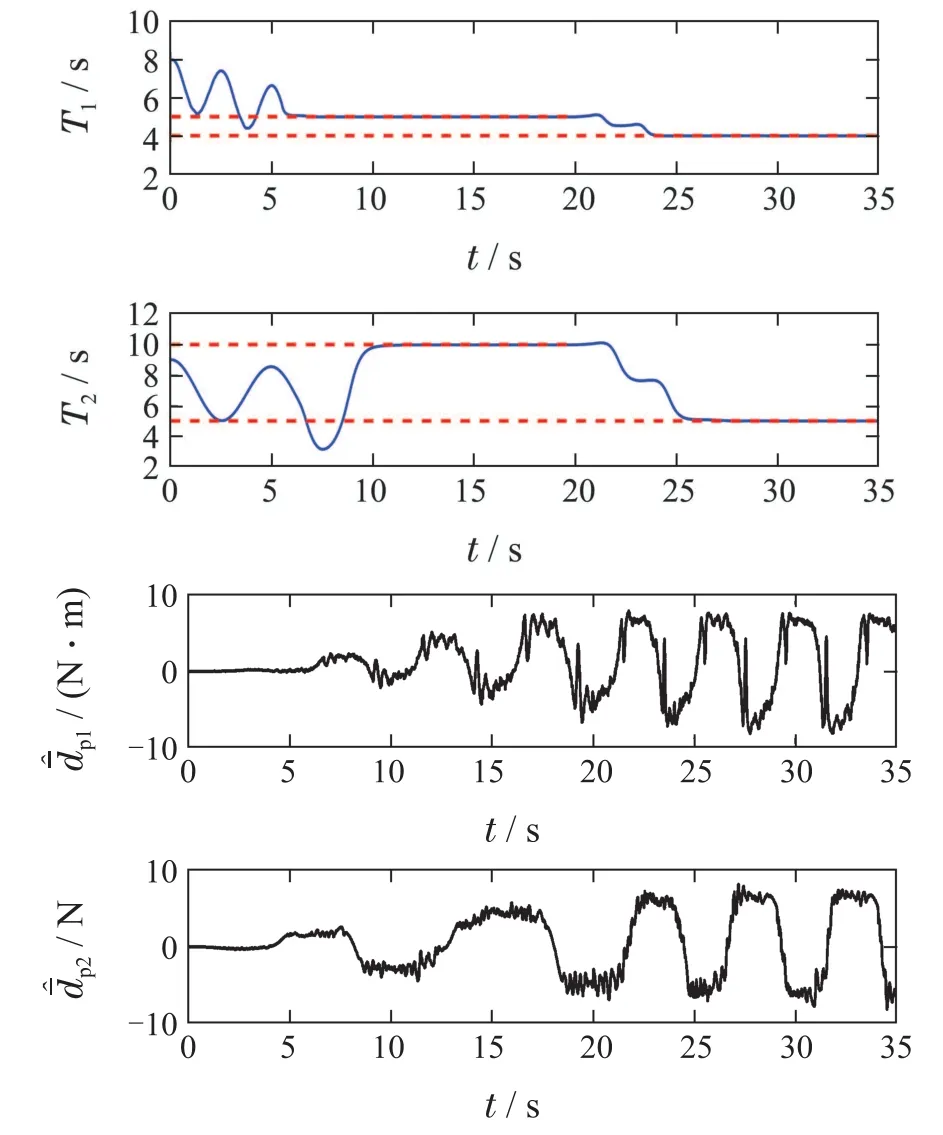
图6 干扰周期改变情况下控制器对周期干扰估计补偿结果Fig.6 Controller’s estimation and compensation for period disturbance under the condition of changing disturbance period

实验2将控制算法中包含的实验平台各项参数修改为m=10 kg,mp=1 kg,J=4 kg·m2;而实际参数为m=5 kg,mp=0.5 kg,J=0.4 kg·m2.

结果如图7-8所示.图7给出了所设计控制器在参数不准确的情况下的控制效果.可以看到,即使存在系统参数不准确问题,控制器依然能够在短时间内控制起重臂q1,绳长q2到达到期望位置,同时抑制负载的摆动并实现负载定位.图8左侧一列给出的是参数正确情况下控制器对非周期干扰的补偿,而右侧一列为参数不正确情况下的补偿图.通过左右两列图的对比可以发现,当系统参数设定不准确时,所带来的干扰可以通过神经网络来进行补偿.说明了对于船用起重机系统,考虑未知干扰的非周期部分是必要的,也证明了神经网络对非周期干扰的补偿能力.在实际作业中,由于设备的尺寸及安装的位置等原因,常常无法精确地获得船用起重机所有的系统参数,而所提方法不依赖于模型参数的准确性,具有良好的鲁棒性,应用前景广阔.

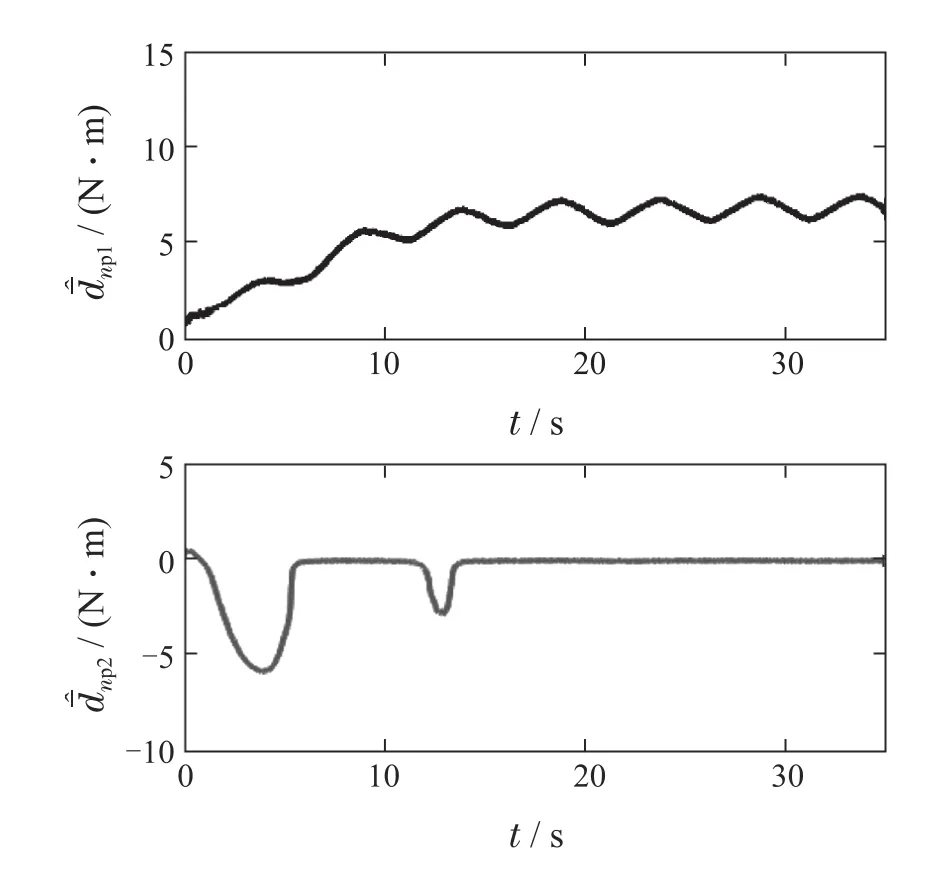
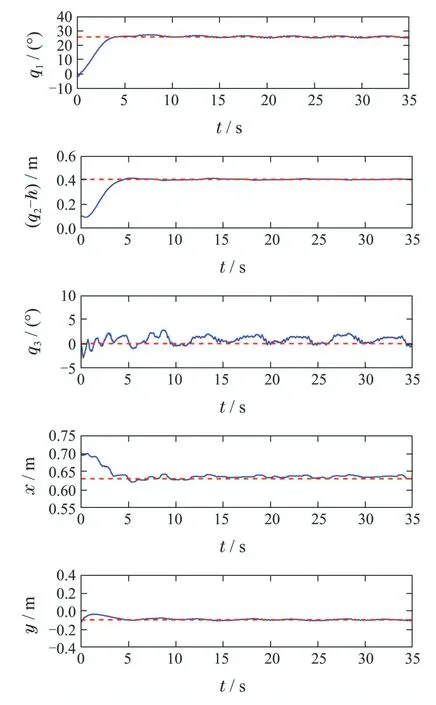
图7 参数不确定情况下的实验结果Fig.7 Experimental results under parameters uncertainty

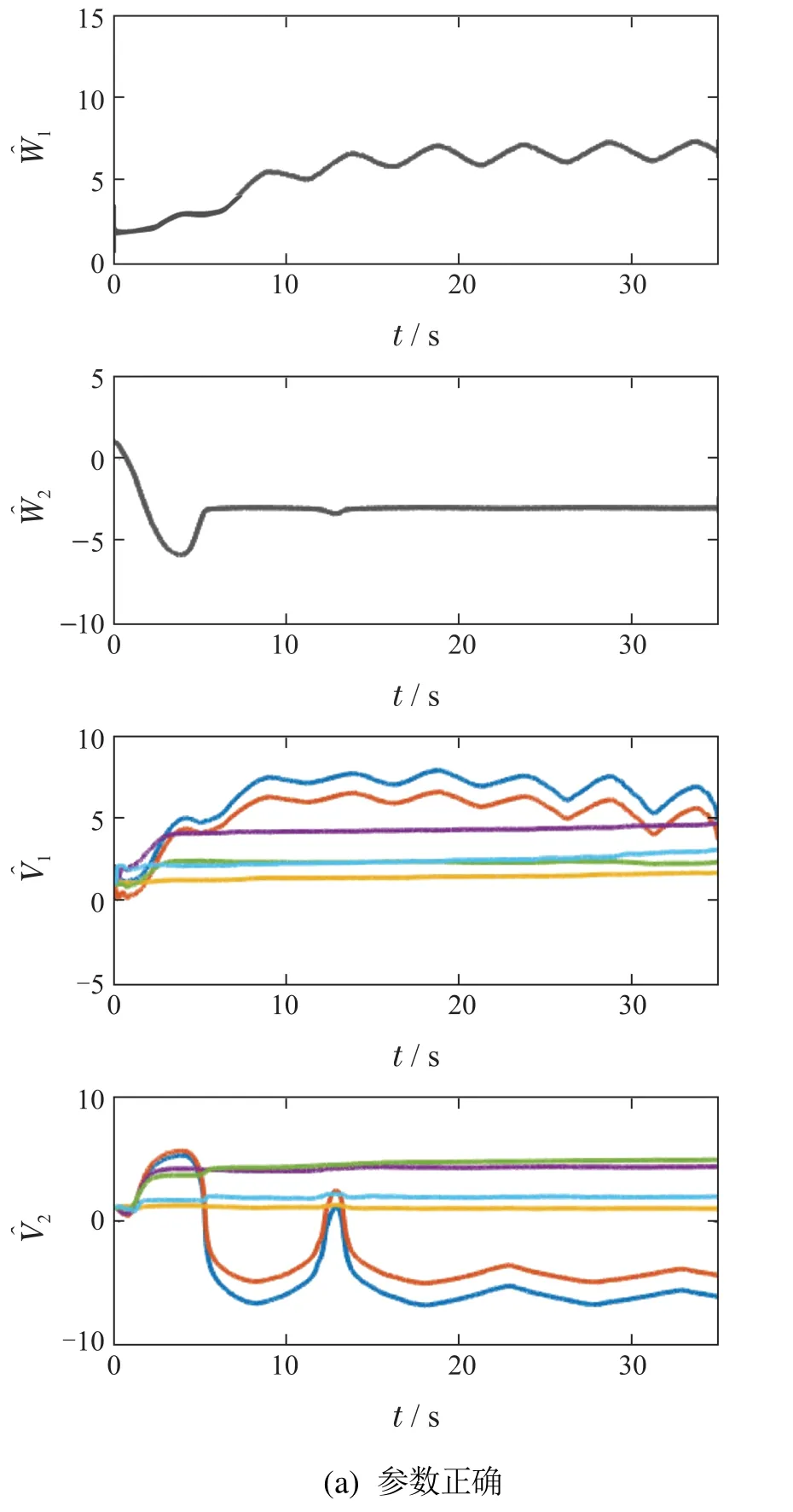
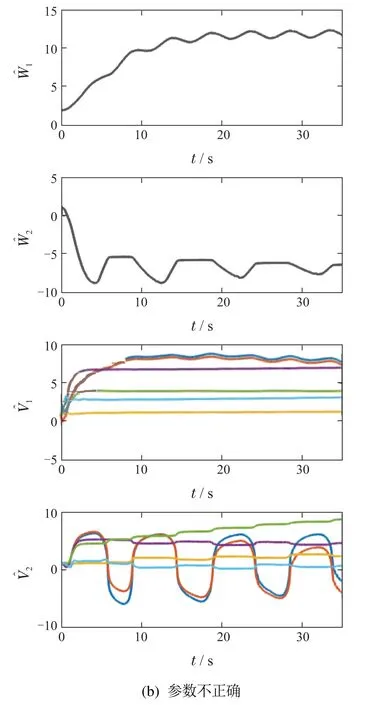
图8 参数不确定情况下控制器对非周期干扰估计补偿对比Fig.8 Comparison of controller’s estimation and compensation for non-periodic disturbance under parameters uncertainty

6 结论

本文针对未知干扰下船用起重机的控制问题提出了一种基于迭代学习和神经网络的方法.该方法不仅能够对未知周期干扰进行周期估计,基于迭代学习做出补偿,还能通过双层神经网络对非周期性干扰进行估计补偿,提升了系统的抗干扰能力.利用Lyapunov方法进行了严格的分析,从理论上证明了期望平衡点的全局有界性.最后,在基于Stewart的船用起重机实验平台上进行了大量实验,充分证明了所提方法在有未知干扰、摩擦、参数不确定等情况下的有效性和鲁棒性.未来会将该控制问题提升到三维层面,在考虑俯仰、升沉、扭转运动的情况下完善控制器设计.

致谢

感谢广东省机器人与智能系统重点实验室,中国科学院深圳先进技术研究院,对本工作的支持！