初等函数中的“创新问题”的思维方法

■江苏省泰兴市第二高级中学 张志峰

“新定义”型问题,主要是指在问题中定义了中学数学中没有学过的一些新概念、新运算、新符号,要求同学们读懂题意,收集反馈处理信息,根据新的定义进行运算、推理、迁移的一种题型。这类题目具有启发性、思考性、挑战性和隐蔽性等特点,是考查同学们的核心素养、挖掘同学们的潜力的较佳题型,因而备受命题者的青睐。本文对初等函数中的“创新问题”的思维方法进行归纳提炼,希望对同学们的复习备考能有所帮助。

归纳1:函数值求解的“创新”——寻求函数对称中心整体代换求解

例1已知函数f(x)=满足条件=1,其中a＞1,则=()。

A.1 B.2 C.3 D.4

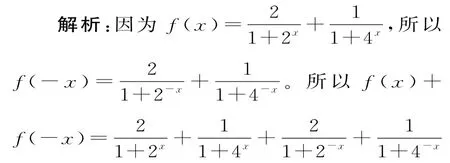
归纳2:自变量与函数值求和中的“创新”——寻求两函数的同一对称中心整体代换求解

例2已知f(x)=,函数g(x)对任意x∈R 有g(2018-2x)=3-g(2x-2013)成立,y=f(x)与y=g(x)的图像有m个交点,为(x1,y1),(x2,y2),…,(xm,ym),则=()。

A.2013mB.2015m

C.2017mD.4m

解析:由g(2018-2x)=3-g(2x-2013),令t=2x-2013,则2018-2x=5-t,g(5-t)=3-g(t),可得y=g(x)的对称中心为,而f(x)=的对称中心为,所以y=f(x)与y=g(x)的图像有m个交点(x1,y1),(x2,y2),…,(xm,ym)关于对称,所以x1+xm=x2+xm-2=x3+xm-3=…=5,y1+ym=y2+ym-2=y3+ym-3=…=3。设x1+x2+…+xm-1+xm=M,则xm+xm-1+…+x2+x1=M,两式相加可得(x1+xm)+(x2+xm-2)+…+(xm-1+x2)+(xm+x1)=2M=5m,所以M=。同理可得y1+y2+…+ym-1+ym=。=x1+x2+…+xm+y1+y2+…+ym==4m。故选D。

提炼:利用换元法探究函数的对称中心是本题的一个创新,求两函数交点的自变量与函数值的和,探究两函数的同一对称中心,利用函数的对称中心整体简化求解是本题的另一个创新。

归纳3:超越方程根的“创新”——借助指数函数和对数函数的对称性寻求切入

例3已知方程2018x=a-x和方程log2018x=a-x(a＞1)的根分别为x1,x2,则的取值范围为()。

提炼:指数函数、对数函数与同一个一次函数构成的方程的根,利用互为反函数其图像关于直线y=x对称探究两根的关系,选主元挖掘隐含条件,构建函数求解范围问题。

归纳4:函数不等式探究中的“创新”——函数的单调性和奇偶性的合理转化

例4已知函数f(x)=2x且f(x)=g(x)+h(x),其中g(x)为奇函数,h(x)为偶函数。若不等式3ag(x)+h(2x)≥0对任意x∈[1,2]恒成立,则实数a的取值范围为_____。

解析:由已知得g(x)+h(x)=2x,注意g(x)为奇函数,h(x)为偶函数,则g(-x)+h(-x)=2-x。又因为g(x)为奇函数,h(x)为偶函数,所以-g(x)+h(x)=2-x。所以h(x)=,g(x)=,代入不等式3ag(x)+h(2x)≥0,得≥0在[1,2]上恒成立。

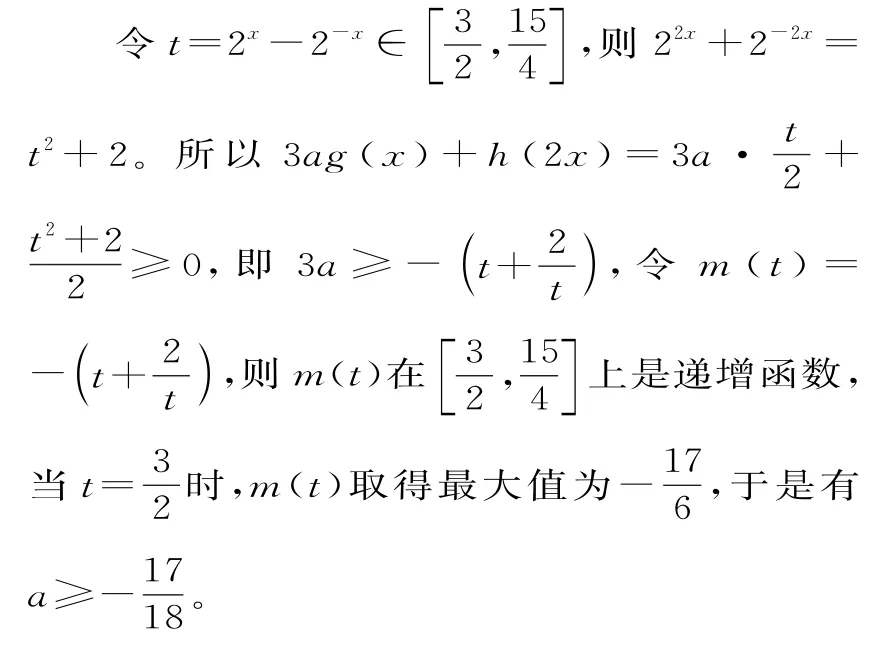
提炼:利用奇偶性构建方程组是本题的一个创新,揭示了定义域关于原点对称的函数都可以写成一个奇函数与一个偶函数的和。函数不等式问题可以转化为含指数变量的不等式恒成立问题,分离参数转化为新函数的值域问题,换元法转化为对勾函数的单调性问题,是待定系数法、构造法、换元法等解题方法的交汇创新。

归纳5:等高线下的最值“创新”——由函数图像探究自变量的关系降元构造函数求解

例5(2021年河北衡水中学一调)已知存在x2＞x1≥0,使得f(x1)=f(x2),则x1f(x2)的取值范围为_____。

解析:作出函数f(x)=的图像,如图1所示。

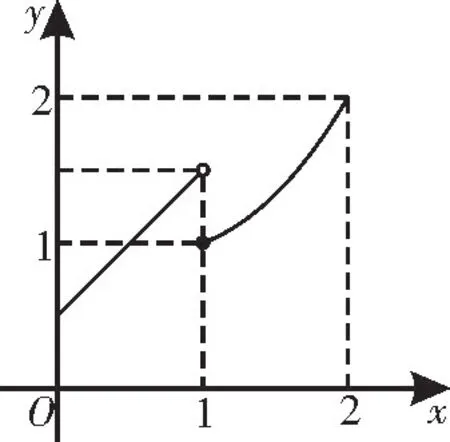
图1

因为存在x2,x1,当x2＞x1≥0 时,f(x1)=f(x2),所以0≤x1＜1。

提炼:对于分段函数或不同函数,当函数值相等时,利用对应自变量满足的关系式求最值,这是等高线下的最值创新。这类问题既要注意等高线隐含的范围,同时还要挖掘等高线下自变量之间的关系,合理地选择主元构建函数在区间上的最值求解。本题关键在于如何求出≤x1＜1。

归纳6:复合函数不等式的“创新”——借助分段函数的图像和性质简化求解

例6若则不等式f(2x2-|x|)≤5的解集为____。

解析:如图2,当x＜0 时,f(x)=-x2+x+2=＜2,且函数为增函数;

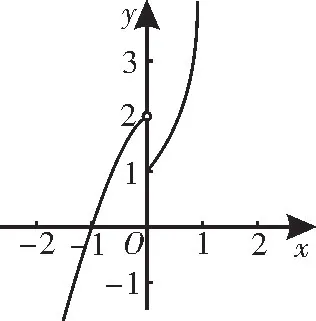
图2

当x≥0时,f(x)=x2+3x+1=≥1,且函数为增函数。

(1)若2x2-|x|＜0,则不等式f(2x2-|x|)≤5恒成立,此时|x|(2|x|-1)＜0,解得0＜|x|＜。

(2)若2x2-|x|≥0,即|x|≥或|x|≤0,则不等式f(2x2-|x|)≤5恒成立。

因为f(1)=5,所以不等式f(2x2-|x|)≤5等价于f(2x2-|x|)≤f(1),则2x2-|x|≤1,即2x2-|x|-1≤0,则|x|≤1。

因为|x|≥或|x|=0,所以≤|x|≤1或|x|=0。

由(1)和(2)知|x|≤1,所以不等式f(2x2-|x|)≤5的解集为[-1,1]。

提炼:关于分段函数的复合函数不等式问题,属于函数图像和性质应用的创新,求解的关键在于整体变量的“对号入座”,运用解析式和单调性作出分段函数的图像,便于寻找分界点和讨论函数的单调性,注意整体变量观念可避免多解或漏解的发生。