用导数研究曲线的切线问题
■江苏省泰兴市第二高级中学 高峰
用导数研究曲线的切线是高考一个主要考点,常与解析几何知识交汇命题,旨在考查同学们对导数的几何意义的正确理解。主要涉及求曲线切线的斜率与方程、曲线切线的条数、曲线的公切线、满足条件的切线是否存在及满足条件的切线的参数范围等问题。
一、曲线在某点处的切线
例1(2021 届四川省遂宁市高三三模)已知函数f(x)=ex-x2+lnx,g(x)=2-ex-lnx。
(1)设曲线y=f(x)在点(1,f(1))处的切线的斜率为k1,曲线y=g(x)在点(1,g(1))处的切线的斜率为k2,求k1+k2的值;
(2)若h(x)=f(x)+g(x),设曲线y=h(x)在点(t,h(t))处的切线与坐标轴围成的三角形的面积为S(t),求S(t)的最小值。
解析:(1)因为f(x)=ex-x2+lnx,所以f'(x)=ex-2x+,所以k1=f'(1)=e-1。
又因为g(x)=2-ex-lnx,所以g'(x)=-ex-,所以k2=g'(1)=-e-1。
所以k1+k2=-2。
(2)h(x)=f(x)+g(x)=2-x2(x>0),h'(x)=-2x,则h'(t)=-2t。
又因为点(t,h(t))为(t,2-t2),所以y=h(x)在点(t,2-t2)处的切线方程为y-(2-t2)=-2t(x-t),故当x=0 时,y=t2+2;当y=0时,x=。
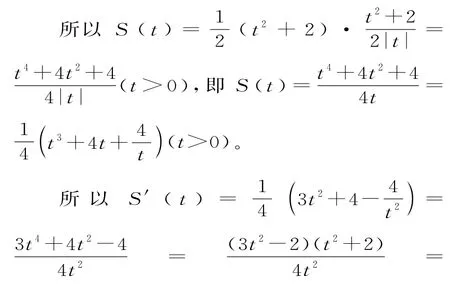

感悟:曲线在某点(x0,f(x0))处的切线,则已知点一定是切点,求切线方程的步骤为:①求出函数f(x)的导数f'(x);②求出切线的斜率k=f'(x0);③写出切线方程yf(x0)=f'(x0)(x-x0),并化简为直线方程的一般式。
二、过某点的曲线的切线
例2(2022 届山东省潍坊市高三上学期期中)已知a∈R,函数f(x)=lnx+a(1-x),g(x)=ex。
(1)讨论f(x)的单调性;
(2)过原点分别作曲线y=f(x)和y=g(x)的切线l1和l2,求证:存在a>0,使得切线l1和l2的斜率互为倒数。
解析:(1)函数f(x)的定义域是(0,+∞),f'(x)=-a。
若a≤0,则f'(x)>0 恒成立,f(x)在(0,+∞)上单调递增。
若a>0,当0<x<时,f'(x)>0;当x>时,f'(x)<0。
所以f(x)在上单调递增;在上单调递减。
(2)f'(x)=-a,g'(x)=ex,设g(x)的切线方程为y=kx,则ex=k,显然k>0,x=lnk,切点为(lnk,k),于是=k,解得k=e,依题意l2的斜率为e,于是l1的斜率为。
设f(x)的切点坐标为(x0,y0),由导数的几何意义知,则x0=。
设G(x)=ln(ex+1)-x,则G'(x)=。
当0<x<时,G'(x)>0,G(x)单调递增,因为G(0)=0,所以>0;
当x>时,G'(x)<0,G(x)单调递减。
又因为G(e3)=ln(e4+1)-e3<5-8<0,所以存在x0∈,使得G(x0)=0,因此关于a的方程a=ln(ae+1)有正数解。
所以存在a>0,使得切线l1和l2的斜率互为倒数。
感悟:对于曲线y=f(x)上“过”点(m,n)的切线问题,一般要先设切点(x0,y0),于是切线为y-n=f'(x0)(x-m),再根据切点在曲线上,得y0=f(x0),切点在切线上,得y0-n=f'(x0)(x0-m),联立方程组,可得切点的坐标。本题探究过原点的两条曲线的切线的斜率互为倒数时参数是否存在的问题,由导数求得l2的斜率为e,从而得l1的斜率为,设f(x)的切点坐标为(x0,y0),利用导数的几何意义得f'(x0)=,得出关于a的方程,再引入新函数,利用导数证明此方程有正数解即可。
三、探究曲线的切线的条数
例3(2022 届重庆市南开中学高三上学期第一次质量检测)已知函数f(x)=lnx+,a∈R。
(1)讨论f(x)的单调性;
(2)若经过坐标原点恰好可作两条直线与曲线y=f(x)相切,求a的取值范围。
解析:(1)f'(x)=,x>0。
当a≤0 时,f(x)在(0,+∞)上单调递增;当a>0时,f(x)在(0,a)上单调递减,在(a,+∞)上单调递增。
(2)设切点的横坐标为x0,则切线方程为y=,将(0,0)代入得lnx0+-1=0,即2a=x0-x0lnx0,关于x0的方程2a=x0-x0lnx0在(0,+∞)内恰有两个解。
令g(x)=x-xlnx,利用导数可求得g(x)在(0,1)上单调递增,在(1,+∞)上单调递减。
又g(1)=1,当x→0 时,g(x)→0,且g(e)=0,故当0<2a<1时,方程g(x)=2a有两个解,所以0<a<。
所以a的取值范围为。
感悟:求曲线的切线的条数一般是设出切点(t,f(t)),由已知条件整理出关于t的方程,把切线的条数问题转化为关于t的方程的实根个数问题。分离参数构建直线与新函数的交点个数,通过导数研究新函数的图像,利用数形结合思想求解。
四、曲线的公切线
例4(2022 届湖北省九师联盟高三上学期质量检测)已知函数f(x)=lnx,g(x)=x2-x+1。
(1)求函数h(x)=f(x)-g(x)的极值;
(2)证明:有且只有两条直线与函数f(x),g(x)的图像都相切。
解析:(1)h(x)=f(x)-g(x)=lnx-x2+x-1的定义域为(0,+∞),且h'(x)=-2x+1=。
当0<x<1时,h'(x)>0;当x>1 时,h'(x)<0。
所以h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以x=1是h(x)的极大值点。
所以h(x)的极大值为h(1)=-1,没有极小值。
(2)设直线l分别与f(x),g(x)的图像切于点(x1,lnx1),(x2,-x2+1)。
由f(x)=lnx可得f'(x)=,所以l的方程为y-lnx1=,即y=·x+lnx1-1。
由g(x)=x2-x+1可得g'(x)=2x-1,所以l的方程y-(-x2+1)=(2x2-1)(x-x2),即y=(2x2-1)x-+1。

当0<x<1时,F'(x)<0;当x>1时,F'(x)>0。
所以F(x)在(0,1)上单调递减,在(1,+∞)上单调递增,所以F(x)min=F(1)=-1<0。
因为F(e2)=ln e2+-2=>0,所以F(x)在(1,+∞)上有一个零点。
由F(x)=lnx+,得F(e-2)=-2+>0,所以F(x)在(0,1)上有一个零点。
所以F(x)在(0,+∞)上有两个零点,故有且只有两条直线与函数f(x),g(x)的图像都相切。
感悟:求曲线的公切线的步骤:第一步,分别设出两个曲线上切点的坐标为P(x1,y1),Q(x2,y2),并求出函数f(x)和g(x)在切点处的导数;第二步,充分考虑题目的已知条件,抓住切线的定义,挖掘题目的隐含条件,寻找解题的等量关系,如同一条切线的斜率和截距相等(尤其两点连线的斜率),以及点既在曲线上又在切线上;第三步,利用方程思想即可得出结论。
五、满足条件的切线是否存在的问题
例5(西安中学2021—2022 学年度第一学期期中)已知函数f(x)=ex-1,g(x)=lnx-1,其中e为自然对数的底数。
(1)当x>0时,求证:f(x)≥g(x)+2。
(2)是否存在直线与函数y=f(x)及y=g(x)的图像均相切?若存在,这样的直线最多有几条?并给出证明。若不存在,请说明理由。
解析:(1)设h(x)=f(x)-g(x)-2=ex-1-lnx-1,x>0,则h'(x)=ex-1-。
因为y=h'(x)在(0,+∞)上为增函数,且h'(1)=0,所以当x∈(0,1)时,h'(x)<0,h(x)为减函数;当x∈(1,+∞)时,h'(x)>0,h(x)为增函数。
所以h(x)min=h(1)=e0-ln 1-1=0,所以h(x)≥0恒成立,所以f(x)≥g(x)+2。
(2)设直线与y=f(x)切于,与y=g(x)切于B(x2,lnx2-1)(x2>0)。

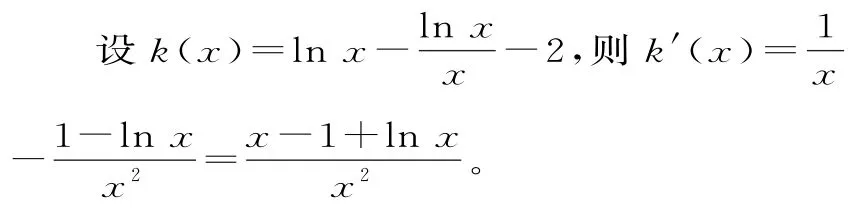
因为y=x-1+lnx在(0,+∞)上为增函数,且x=1时,y=0,所以当x∈(0,1)时,k'(x)<0,h(x)为减函数;当x∈(1,+∞)时,k'(x)>0,h(x)为增函数。所以k(x)min=k(1)=-2<0。
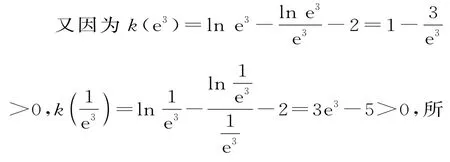

感悟:判断符合条件的切线是否存在,或根据切线满足条件求参数的值或范围,求解思路是把切线满足的条件转化为关于斜率或切点的方程或函数,再根据方程根的情况或函数的性质去求解。

