函数与导数中的不等式问题

■广东省佛山市顺德区容山中学 潘敬贞

函数与导数中的不等式问题一直是高考考查的热点和难点问题,主要包括两种类型:已知不等式求参数的范围和证明不等式。该类问题的求解对同学们的分析问题、转化与化归、代数变形、构造新函数、分类讨论、推理论证、运算求解等能力要求比较高。本文结合实例对常见的函数与导数中的不等式问题进行归纳、梳理,主要目的是加强同学们对该类题备考的针对性,提高解决该类问题的能力,从而提高高考竞争力。

一、已知不等式求参数的范围

例1已知函数f(x)=(x-1)exa(x2+1),x∈[1,+∞)。

(1)讨论函数f(x)的单调性;

(2)若f(x)≥-2a+lnx,求实数a的取值范围。

解析:(1)略。

(2)令g(x)=f(x)+2a-lnx=(x-1)ex-a(x2-1)-lnx,注意到g(1)=0,则问题转化为g(x)≥0在x∈[1,+∞)上恒成立。

g＇(x)=xex-2ax-。

若a＞,则g＇(1)=e-2a-1＜0;g＇(ln(2a+1))=ln(2a+1)-,因为2a+1＞e,所以ln(2a+1)＞1,g＇(ln(2a+1))＞0。所以存在x0∈(1,ln(2a+1)),使得g＇(x0)=0。

当x∈(1,x0)时,g＇(x)＜0,g(x)单调递减,所以g(x)＜g(1)=0,不满足题意。

若a≤,则g＇(x)≥xex-(e-1)x=x[ex-(e-1)]-。

当x＞1时,x[ex-(e-1)]＞1,0＜＜1,所以g＇(x)＞0,g(x)在[1,+∞)上单调递增,所以g(x)≥g(1)=0,满足题意。

综上可得,a≤。

评注:解答本题的关键是由g＇(1)=0得a=,后面只需讨论a＞和a≤时函数g(x)的符号即可。

例2已知函数f(x)=aex-2ax-2(a≠0)。

(1)讨论函数f(x)的单调性;

(2)是否存在a∈(0,1),使得对于任意实数x,都有f(x)+＞0?

解析:(1)f＇(x)=aex-2a=a(ex-2),令f＇(x)=0,得x=ln 2。

若a＞0,当x∈(-∞,ln 2)时,f＇(x)＜0,函数f(x)单调递减;当x∈(ln 2,+∞)时,f＇(x)＞0,函数f(x)单调递增。

若a＜0,当x∈(-∞,ln 2)时,f＇(x)＞0,函数f(x)单调递增;当x∈(ln 2,+∞)时,f＇(x)＜0,函数f(x)单调递减。

(2)方法1:f(x)+=aex-2ax-2+＞0,可变形为ae2x-(2ax+2)·ex+(x2+2x)＞0。

令g(x)=ae2x-(2ax+2)ex+(x2+2x),则g＇(x)=2ae2x-(2ax+2a+2)ex+(2x+2)=2(aex-1)(ex-x-1)。

令h(x)=ex-x-1,则h＇(x)=ex-1,由h＇(x)=0,得x=0。

当x∈(-∞,0)时,h＇(x)＜0,函数h(x)单调递减;当x∈(0,+∞)时,h＇(x)＞0,函数h(x)单调递增。

因此,不存在a∈(0,1),使得对于任意实数x,都有f(x)+＞0。

由(1)知,当a＞0时,f(x)min=f(ln 2)=2a-2aln 2-2。

g＇(x)=,令g＇(x)=0,得x=。

所以g(x)在(-∞,)上单调递增,在上单调递减,在上单调递增。

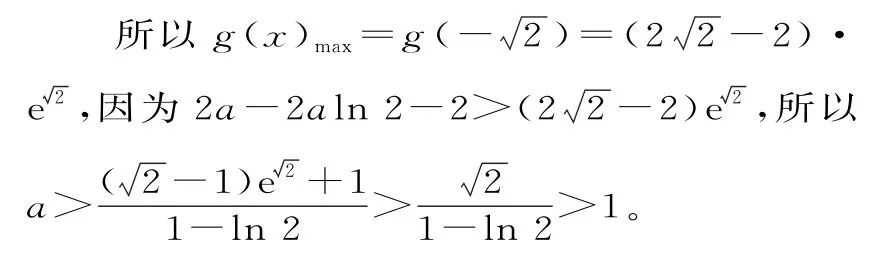
因此,不存在a∈(0,1),使得对于任意实数x,都有f(x)+＞0。

方法3:假设存在a∈(0,1),使得对于任意实数x,都有f(x)+＞0,即aex-2ax-2+＞0。令h(x)=ex-2x,则h＇(x)=ex-2。当x∈(-∞,ln 2)时,h＇(x)＜0,h(x)单调递减;当x∈(ln 2,+∞)时,h＇(x)＞0,h(x)单调递增。所以h(x)min=h(ln 2)=2-2ln 2＞0,所以ex-2x＞0,所以a＞恒成立。

令F(x)=,则F＇(x)=。

令Q(x)=ex-x-1,则Q＇(x)=ex-1。当x∈(-∞,0)时,Q＇(x)＜0,Q(x)单调递减;当x∈(0,+∞)时,Q＇(x)＞0,Q(x)单调递增。所以Q(x)≥Q(0)=0,所以ex≥x+1。

而获得了知识和美德的人，就可以出色地运用其天生就具备的武器(即各种能力)，而美德一旦武装起来就能形成极强的能力；如果人们的品德败坏了，比如极其邪恶和残暴，无比放荡和贪婪，就会把我们天生的武器用于做极恶劣的事情。“不公正被武装起来将会是莫大的祸害。”[2](P7)善德与恶德对于个人和团体的生活之影响十分巨大，所以，政治的作用就是要采取优良政体，或者促使时下的各种政体能够得到改善，其标准就是：有效地安排各种善，并使美德的价值优先；同时政体的安排要有助于公民获得美德，并且可以按照政体能在多大程度培养公民的完整美德来衡量其优良程度。

令g(x)=x2-ex,则g＇(x)=2x-ex＜0,所以g(x)在R 上单调递减。

又g(-1)=1-＞0,g(0)=-1＜0,所以∃x0∈(-1,0),使得g(x0)=0,从而F＇(x0)=0,此时。

当x∈(-∞,x0)时,F＇(x)＞0,F(x)单调递增;当x∈(x0,+∞)时,F＇(x)≤0,F(x)单调递减。所以F(x)max=F(x0)=＞1,所以a＞1,矛盾。

因此,不存在a∈(0,1),使得对于任意实数x,都有f(x)+＞0。

评注:本题是以探究存在性问题进行设问,具有浓厚的探究味道,但本质上和已知不等式求参数范围是一致的,本题的方法1 是正面突破,将问题转化为求函数的最值问题,通过一系列推导和求解得出矛盾,最后下结论,这是这类问题的一般解法,但过程有点烦琐;方法2 是将问题转化为f(x)min＞g(x)max,从而求得实数a的取值范围,最后得出结论,该思路也非常清晰、自然,解答过程简洁,是一种好的解法;方法3是通过分离参数,然后构造新函数,该解法容易理解,也常用,但对运算能力要求比较高,解答过程比较繁杂,没有一定的数学功底很难完整地解答出来。

二、证明函数不等式

有关证明不等式问题,一般有转化后求函数的最值问题,极值点偏移问题,对数均值不等式问题,有时还需要对函数进行同构等。

例3已知函数f(x)=x2+ax+2lnx(a为常数)。

(1)当a≤4 时,讨论函数f(x)的单调性;

(2)若f(x)存在两个极值点x1,x2,且|x1-x2|≤,证明:|f(x1)-f(x2)|≤-4ln 2。

解析:(1)函数f(x)的定义域为(0,+∞)。

f＇(x)=2x+a+。

设g(x)=2x2+ax+2(x＞0)。

当-4≤a≤4时,Δ≤0,2x2+ax+2≥0成立,则f＇(x)＞0,所以函数f(x)在(0,+∞)上单调递增。

(2)由(1)知函数f(x)的两个极值点x1,x2满足2x2+ax+2=0,所以x1x2=1,x1+x2=。

不妨设0＜x1＜1＜x2,则f(x)在(x1,x2)上是减函数,故f(x1)＞f(x2)。

评注:本题第(2)问根据题意利用韦达定理将参数消掉,进而将问题转化为求函数的最值问题,解题过程中的换元、变形是关键,试题难度较大,需要丰富的解题经验和较高的数学综合能力。

函数不等式问题一直是高考考查的热点问题,也是难点问题,一般都是考卷中的压轴题,该类题的解决对同学们的数学能力要求较高,不仅需要丰富的解题经验,还需要很强的推理论证和运算求解能力。只有勤于思考,经常归纳解题思路,提炼思想方法,不断反思小结,从而提高自己的数学综合能力,才能在高考考场中击败函数与导数压轴题。