函数性质应用中的“数学素养”

■江苏省泰兴市第二高级中学 李明

函数性质是整个高中数学的核心内容,是高中数学的主线,所有知识均可与函数建立联系,都可围绕这一主线展开,函数的单调性、奇偶性和周期性更是高考考查的重中之重,常与方程、不等式等知识结合起来考查,本文探究函数性质应用中的“数学素养”。

一、抽象函数性质探究中的“思维方法”

例1(2021年江苏省苏州市高新区第一中学高三月考)已知定义在R 上的函数f(x)满足:对任意x,y∈R,都有f(x+y)=f(x)+f(y),且当x＞0时,f(x)＞0。

(1)求f(0)的值,并证明f(x)为奇函数;

(2)判断函数f(x)的单调性,并证明;

(3)若f(k·2x)+f(4x+1-8x-2x)＞0对任意x∈[-1,2]恒成立,求实数k的取值范围。

解析:(1)令x=y=0,得f(0+0)=f(0)+f(0),所以f(0)=0。

令y=-x,得f(x-x)=f(x)+f(-x)=f(0)=0,所以f(-x)=-f(x),故f(x)为奇函数。

(2)设x2＞x1,则x2-x1＞0。

由f(x2)=f(x1+x2-x1)=f(x1)+f(x2-x1)⇒f(x2-x1)=f(x2)-f(x1)。

因为当x＞0时,f(x)＞0,所以f(x2-x1)=f(x2)-f(x1)＞0⇒f(x2)＞f(x1)。

所以f(x)是增函数。

(3)由题知f(k·2x+4x+1-8x-2x)＞0。

又y=f(x)是定义在R 上的增函数,所以k·2x+4x+1-8x-2x＞0 对任意x∈[-1,2]恒成立,所以k·2x＞2x+8x-4x+1,所以k＞1+22x-2x+2。

令2x=t,t∈,则f(t)=t2-4t+1,所以k＞f(t)max。

当t=4时,f(t)max=f(4)=16-16+1=1,所以k＞1。

体验:对于抽象函数的有关问题,其求解的思维方法是:合理运用对应法则和题设条件,多次赋值探究奇偶性;依据定义、题设及法则证明其单调性;利用奇偶性和单调性转化为函数不等式,通过不等式恒成立求参数的取值范围;常用变量分离法、换元法、构造函数法等求最值。主要考查同学们的数学运算、构建函数模型及逻辑推理等能力。

二、函数对称性应用中的“整体思维”

例2(2021 年湖南省衡阳市雁峰区校级月考)已知函数f(x)=。

(1)求证:存在定点M,使得函数f(x)的图像上任意一点P关于点M对称的点Q也在函数f(x)的图像上,并求出点M的坐标;

(3)对于(2)中的Sn,求证:对于任意的n∈N*,都有lnSn+2-lnSn+1＞。

解析:(1)函数f(x)的定义域为(0,1)。设M(a,b),若使得函数f(x)的图像上任意一点P关于点M对称的点Q也在函数f(x)的图像上,则必有f(x)+f(2a-x)==2b,对于x∈(0,1)恒成立,所以1-2a=0,1=2b,所以a=b=。所以存在定点,使得函数f(x)的图像上任意一点P关于点M对称的点Q也在函数f(x)的图像上。

(2)由(1)得f(x)+f(1-x)=1。

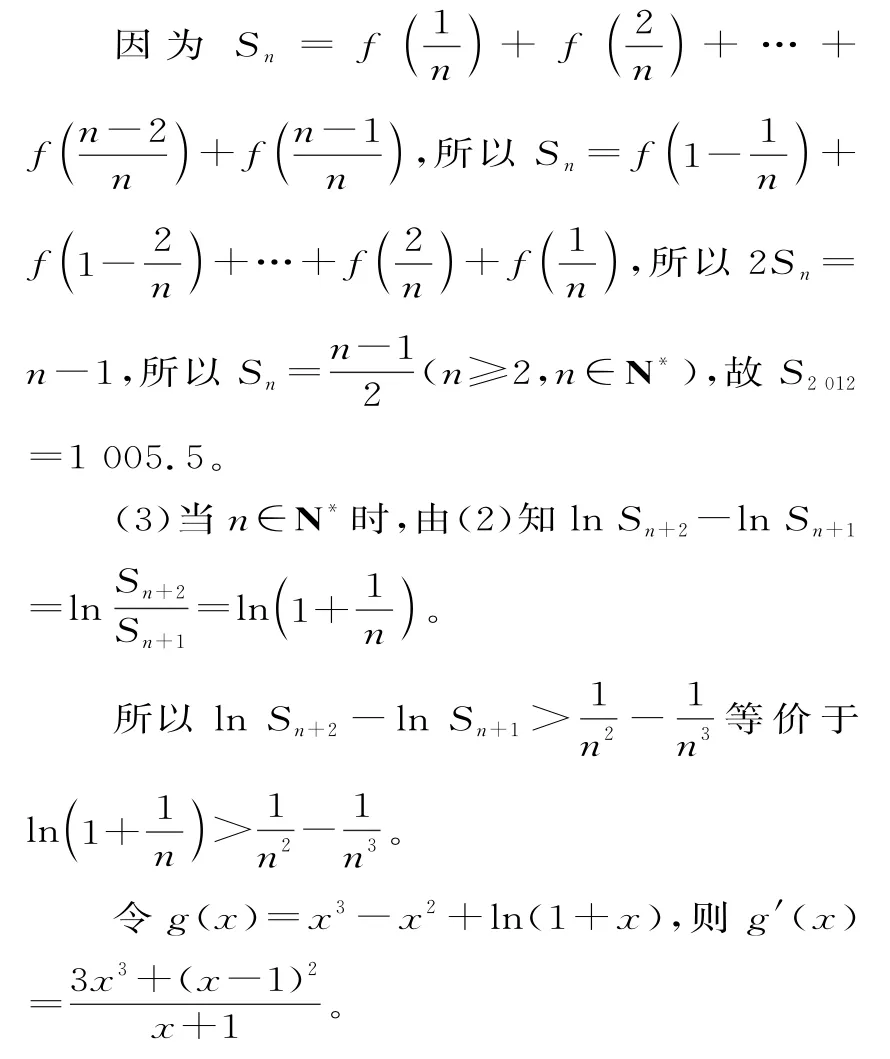
所以当x∈(0,+∞)时,g＇(x)＞0,即函数g(x)在(0,+∞)上单调递增,又g(0)=0,所以g(x)＞g(0)=0,即x3-x2+ln(1+x)＞0恒成立。

故当x∈(0,+∞)时,有ln(1+x)＞x2-x3成立,取x=∈(0,+∞),则有成立。

体验:当函数f(x)满足f(x+a)+f(b-x)=c时,函数y=f(x)的图像关于点对称;利用“函数的对称中心的特征,采用倒序相加法整体思维”可简化求解函数值构成的数列的求和问题。对于函数不等式的证明,可用分析综合法转化为函数值的大小关系,构造新函数研究单调性进行求证。凸显函数性质应用中的逻辑推理、整体思维、构建函数模型等素养。

三、最值探究中的“换元法和分类讨论”

例3(2022 届东北育才学校科学高中部高三第一次模拟)已知函数f(x)=+(sinx+cosx)·(sinx-cosx)+1。

(1)常数ω＞0,若函数y=f(ωx)在区间上是增函数,求ω的取值范围;

(2)若函数g(x)=-1 在上的最大值为2,求实数a的值。

解析:(1)利用三角恒等变换公式化简得f(x)=+sin2xcos2x+1=2(1-sinx)sinx+sin2x-cos2x+1=2sinx,则y=f(ωx)=2sin(ωx)。

故ω的取值范围为(0,1]。

(2)由(1)可得g(x)=-1=sin 2x+a(cosx-sinx)--1,x∈。

设t=cosx-sinx,则sin 2x=2sinxcosx=1-t2。

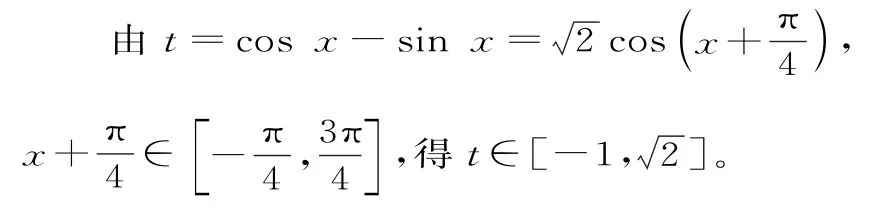
综上,实数a的值为-2或。

体验:三角公式±sinxcosx=,揭示了二次函数关系,同时给出了“平方沟通的三角变换方法”,奠定了换元法化归构造外层为二次函数在区间上的最值,借助对称轴和区间分类研究最值问题。形如y=asin2x+bsinx+k,可先设sinx=t,转化为关于t的二次函数求值域;形如y=asinxcosx+b(sinx±cosx)+c,可先设t=sinx±cosx,转化为关于t的二次函数求值域。利用换元法处理三角函数的最值时,注意确定新元范围,如令t=sinx,t∈[-1,1];t=sinx+cosx,t∈等。

四、复合函数开放探索研究中的“推理验证”

例4(2021 年江苏省淮安市洪泽区高三月考)现有如下三个条件:在①f(x)+f(-x)=0;②f(x)-f(-x)=0;③f(-2)=-f(2)。从这三个条件中选择一个,补充在下面问题中,并给出解答。

已知函数f(x)=(a∈R)满足____。

(1)求a的值;

(2)若函数g(x)=2f(-x)+1-,证明:g(x2-x)≤。

解析:选择条件①f(x)+f(-x)=0。

选择条件②f(x)-f(-x)=0。

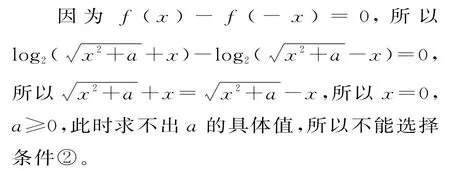
选择条件③f(-2)=-f(2)。

体验:复合函数研究中的开放探索,按照题设要求合理选择条件,一一进行推理验证,推理验证过程中涉及奇偶函数的特征、对数运算及复合函数的最值探究。