基于滑模变结构的高速动能弹制导控制算法*

焦思洋，潘涛，孔哲，刘宝宁

（西安航天动力技术研究所，陕西 西安 710025）

0 引言

高速动能导弹作为一种新型现代防御武器，其作战目标是地面装甲坦克，采用飞行高度10 m左右的低空贴地式飞行，其战术特点是利用自身高速度、大动能直接碰撞摧毁目标［1］。与传统反坦克导弹有所不同，高速动能弹的马赫数高达5，需采用响应速度更快的脉冲发动机直接力控制策略［2］。当脉冲发动机在低空环境中点火工作时，会引起周围流场发生剧烈变化［3-4］。由于高速动能弹本身的高速度大动能、气动参数偏高，剧烈的流场变化会产生较大的干扰力矩，采用传统控制方法可能会造成控制精度不佳［5］。因此，本文选择鲁棒性相对较强的滑模变结构控制方法，设计出一种新型基于滑模变结构的高速动能弹制导控制方法，来实现对目标的精准打击。

1 弹体模型建立

1.1 弹体结构模型建立

本文谈论的高速动能导弹弹体前端采用阵列式脉冲发动机，共7排从弹体头部往后排列，弹体尾部无气动舵，依靠脉冲发动机进行姿态控制。其结构布局如图1所示。

图1 弹体结构示意图Fig.1 Str uctur e diagram of missile

1.2 高速动能弹动力学模型建立

高速动能弹为滚转导弹，在分析弹体运动时，在建立常用的地面系Oxyz、弹体系Ox1y1z1、弹道系Ox2y2z2、速度系Ox3y3z3之外，通常引入2个新的坐标系：准弹体系Ox4y4z4、准速度系Ox5y5z5。根据滚转导弹运动方程组，建立高速动能弹动力学模型。

2 基于滑模变结构的高速动能弹控制算法

高速动能弹控制系统主要由制导站、惯性测量单元、制导控制算法、执行机构（脉冲发动机）等单元组成，其结构如图2所示。本文主要针对高速动能弹的制导控制算法进行设计研究。高速动能弹通常以低空贴地飞行的方式打击地面装甲武器，采用三点法导引更加简单易行且抗干扰性能好。三点法的原理是：作战过程中导弹始终处于制导站与目标的连线上，以此方式导引弹体命中目标［6］。本文将设计出一种三点法导引的滑模变结构制导控制算法，实现弹体对目标的精确打击。

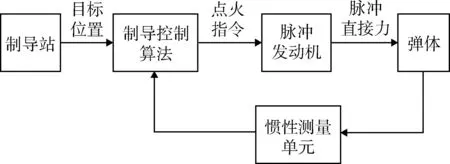
图2 高速动能弹控制系统结构示意图Fig.2 Str uctur e diagram of hyper velocity kinetic energy missile’s control system

2.1 滑模变结构控制

滑模变结构控制的控制原理是：在系统ẋ=f(x)的状态空间中，设计一个切换面s（x）=0将状态空间分为s>0及s<0 2个部分。通过控制策略的设计，使得系统在s（x）=0两侧拥有不同的结构，这种结构的变化迫使切换面以外的点均运动趋近于切换平面，随后在切换平面附近进行小幅度的振荡运动［7］，通过这种方式达到控制系统状态的目的。

2.2 基于滑模变结构控制的控制算法推导

以俯仰通道为例，制导过程中的导弹、目标位置关系如图3所示，O为地面制导站位置，M为导弹当前位置，T为打击目标位置，直线OT为飞行过程中的基准线，θt为制导站与目标的连线与水平面的夹角。

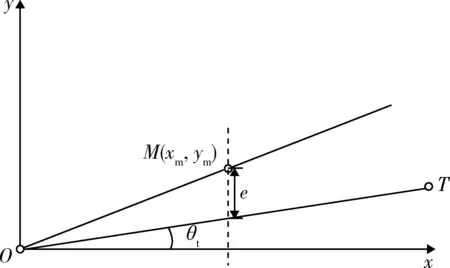
图3 导弹与目标位置关系示意图Fig.3 Position schematic of missile and target

设e为导弹纵向位置（ym）与基准线OT的纵坐标差值，即e=ym-xmtanθt。因高速动能导弹打击的地面目标一般为地面固定目标或是移动速度较慢的目标，假设θt的值不会随时间变化而变化。可以进一步推导得出：

式中：vx，vy和ax，ay分别为弹体x，y方向的速度和加速度。

针对高速动能弹的弹体特性，可采用俯仰通道扰动方程组最简形式［8］：

式中：ϑ为俯仰角；θ为速度倾角；α为攻角；δz为舵偏角（在不含气动舵的直接力控制系统中表示纵向直接力）；Fgy，Mgz为y向干扰力和z向干扰力矩；a22，a24，a25，a26，a34，a36为动力系数。

暂不考虑干扰影响，由上述方程组可得，

式中：v为俯仰通道合速度。

设滑模变结构算法中的切换函数为s=ce+̇，其中c为常数。则

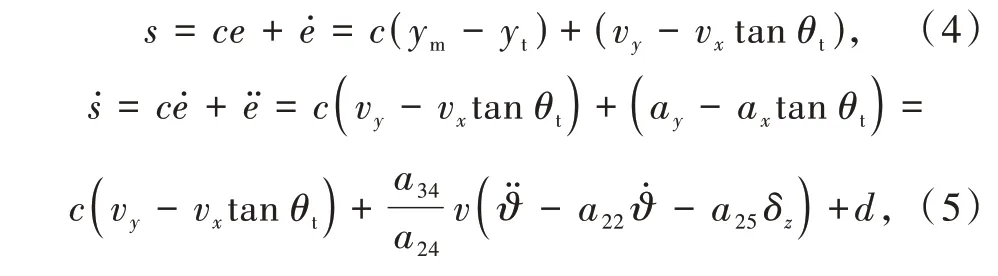
式中：d为因模型简化、高速动能弹脉冲喷流形成干扰等原因导致的̇变化量，假设d的取值会在一个界值范围内，即|d|≤D，

̇=0时，

若要滑模算法稳定，必须保证̇<0。取η>D，设计滑模控制律为

定义李雅普诺夫函数为

则

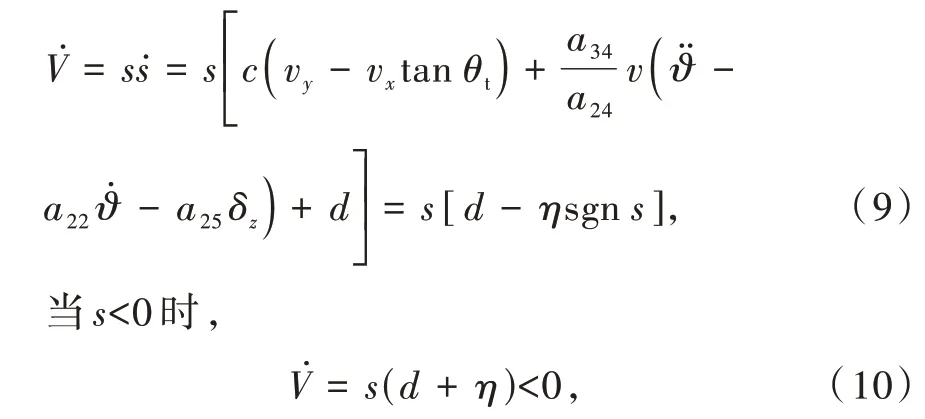
当s>0时，

可证系统渐进稳定。

2.3 参数设定

2.2 节推导出的滑模控制律即式（7）中有2个参数c和η需要设计确定。在滑模变结构算法中，c的取值影响位置误差在控制算法中的权重，同时也决定了收敛速度；η则用来克服干扰误差项造成的影响。这2个参数选取不当会造成控制系统精度不够、抖振加剧等问题［9］。本文将根据高速动能弹自身的弹体特性及作战目标需求，来对滑模控制算法相关参数的设计进行整定。

由式（7）可以推导出关于η的关系式为

初步选取一个参数c的数值，对高速动能弹作战飞行时的相关数据进行取值：脉冲发动机的最大推力为400 N，故取δz为400 N；根据经验分析动能弹的运动规律，对俯仰角速度̇和角加速度̈取期望的最大值。通过式（12）对参数η进行实时计算，选取整个过程中的最大值，作为算法中参数η的取值。

将整个系统控制框图简化后如图4所示，计算求出弹体开环回路的传递函数，得到开环传递函数的开环增益。滑模制导控制算法中c为位置误差项系数，当输入位置误差项为1时，输出的位置误差为Kc。现设定弹体飞行过程中允许的最大位置误差（输出位置误差）为2 m，可以反推出参数c的取值。之后再次进行对η的迭代设计，可以达到更加精细化的结果。最终推算得出针对本文研究的高速动能弹的参数c取值为1.8，η取值为20。

图4 系统简化框图Fig.4 Simplified block diagr am of the system

设定导弹起始位置为（0，3）m，位置目标为（4 000，0）m，在仿真软件中对导弹进行弹道仿真。用设计推算出的滑模变结构制导控制算法对弹体进行控制，仿真得到相关结果如图5～8所示。

图5 射程随时间的变化图Fig.5 Range-time

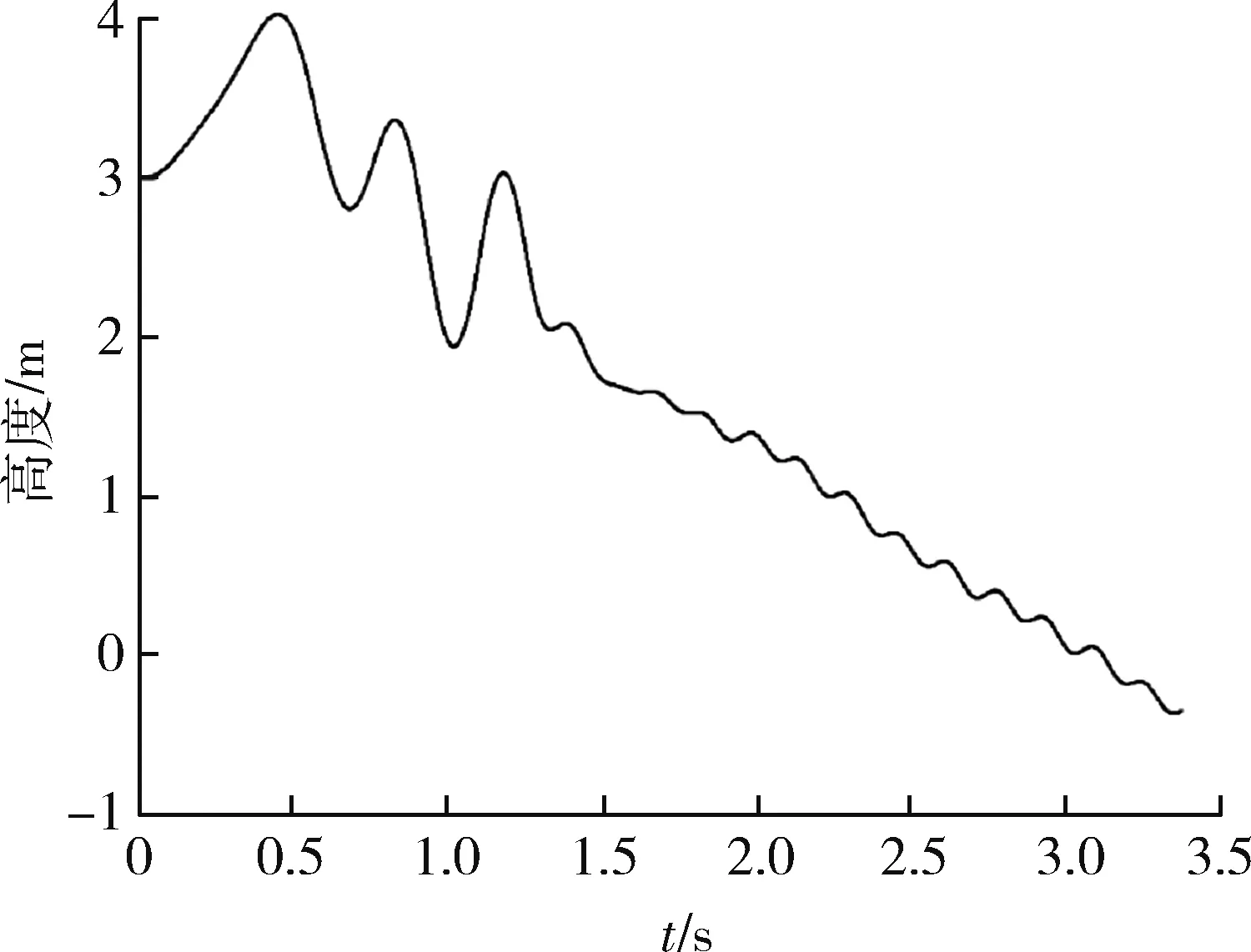
图6 高度随时间的变化图Fig.6 Height-time

图7 俯仰角随时间的变化图Fig.7 Pitch-time

从仿真结果可以看出，弹体的落点坐标为（4 000，-0.3）m，表明本文设计的滑模变结构制导控制算法能够控制弹体命中目标。但俯仰角和俯仰角速度的变化曲线表明，稳定后的滑模抖振幅度较大。

图8 俯仰角速度随时间的变化图Fig.8 Pitch angular velocity-time

2.4 滑模变结构抖振问题研究

从理论的角度来看，控制算法的滑动模态可以根据任务需求进行设计，并且系统的滑模运动与外界的干扰因素及自身参数变化无关，这也就是滑模变结构控制相比于传统控制方法鲁棒性更强一些的原因［10］。

理想的滑模变结构控制算法，假设结构变换过程中无时间和空间的滞后即具有理想的开关特性，且所有状态量均精确无误，滑动模态可以实现光滑运动且渐进稳定于原点［11］（即不会产生抖振）。但实际中，系统的轨迹到达切换面时具有一定的速度，由于开关的时间、空间滞后，算法对状态的控制作用有一定的延迟时间，故运动点会在惯性的作用下穿越切换面，最终导致滑模抖振。因此，滑模抖振问题不可避免［12］，需要采取一定的措施对其进行削弱。本文将采取边界层法和指数趋近律法2种方法对抖振问题进行处理。

2.4.1 边界层法

由上文分析知，滑模变结构控制算法理想的开关切换特性在实际中根本无法存在，通常在切换平面附近设计一个边界层Δ，在边界层外时，使用切换控制，使系统状态能快速趋于滑动模态；在边界层内时，使用线性化反馈控制［13］。具体做法为：用饱和函数sat（s）代替滑模变结构控制算法中符号函数sgns。

式中：k=，则经边界层法处理后的滑模控制律表达式为

2.4.2 指数趋近律法

趋近律法的整体思路是通过使整个系统状态轨迹能够较为平滑地通过滑动模态，从而避免不断切换控制结构所造成的系统抖振［14］。本文采用目前常用的指数趋近律法［15］：

式中：ṡ=ks为指数趋近项，其解为s=s(0)e-kt，为指数形式。

因此，当系统状态距离切换平面较远时，能够快速趋近于切换面；而当运动逐渐接近切换平面时，趋近速度会大大降低，从而在快速趋近的同时适量削弱抖振。增加ṡ=-εsgns项的作用在于，当s接近0的时候，趋近速度不会为0而是ε，能够确保在有限时间内到达切换面。

将式（14）代入上文关于ṡ的表达式（5）中，得

则滑模控制律为

由于干扰项d的值未知，无法直接应用，需对其进行设计处理。取控制律为

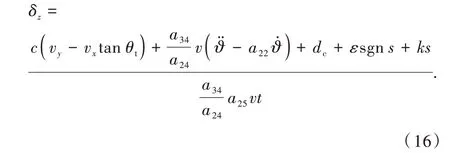
将控制律式（16）代入关于ṡ的表达式（5）中，得

假设干扰项d的取值范围为：dL≤d≤dU。为了保证sṡ<0，可选取

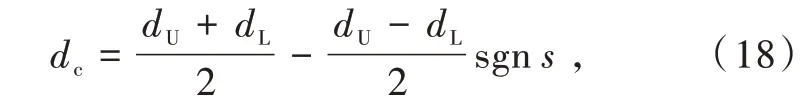
当s>0时，̇=dL-d-εsgns-ks<0，

当s<0时，̇=dU-d+ε-ks<0.

满足滑模收敛条件，确保系统稳定。

3 仿真分析

3.1 算法仿真

对滑模变结构制导控制算法分别采用边界层法和指数趋近律法进行抖振削弱，使用软件对其建模仿真，仿真结果如图9～15所示。

图9 射程随时间的变化图Fig.9 Range-time

图10 高度随时间的变化图Fig.10 Height-time

图11 侧偏随时间的变化图Fig.11 Yaw-time

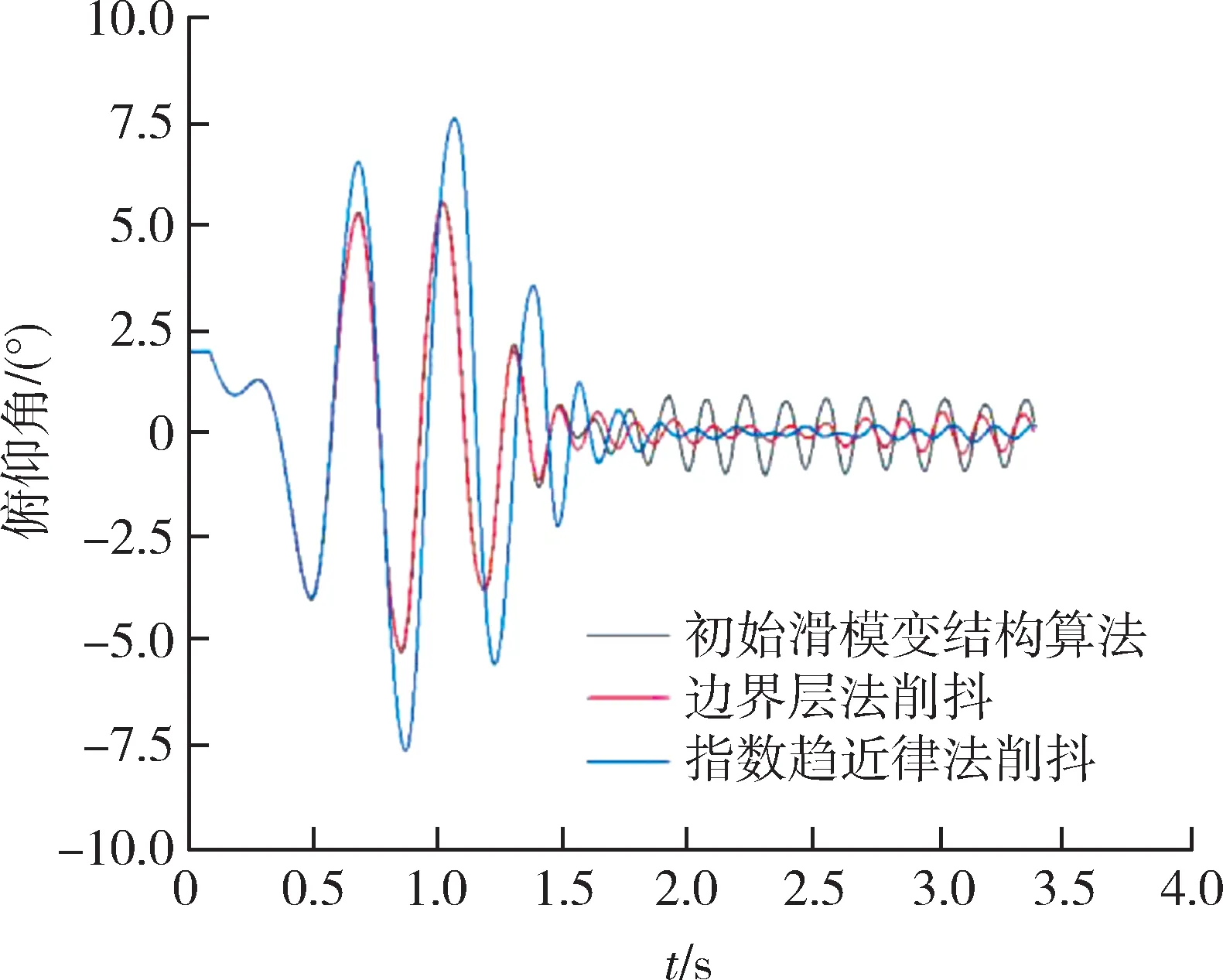
图12 俯仰角随时间的变化图Fig.12 Pitch-time

图13 俯仰角速度随时间的变化图Fig.13 Pitch angular velocity-time

图14 偏航角随时间的变化图Fig.14 Yaw angle-time

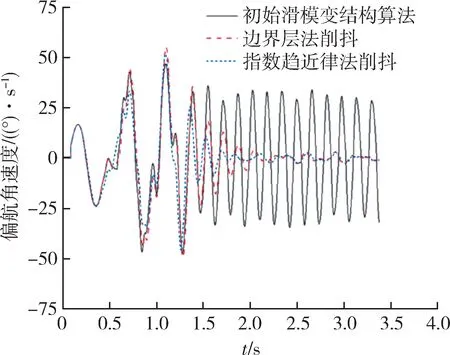
图15 偏航角速度随时间的变化图Fig.15 Yaw angular velocity-time

设定导弹初始位置为（0，3，0）m，目标位置为（4 000，0，0）m。从仿真结果来看，弹体的落点位置在（4 000，-0.2，0.1）m，表明滑模控制算法能够控制弹体命中目标。俯仰通道上，稳定后的俯仰角在±1°之间振荡，俯仰角速度在±45（°）/s之间振荡；偏航通道上，稳定后的偏航角在±1°之间振荡，偏航角速度在±45（°）/s之间振荡，抖振幅度都较大。经边界层法处理的算法能使稳定后俯仰角、俯仰角速度、偏航角、偏航角速度的振荡浮动分别处于±0.5°，±15（°）/s，±0.04°，±1.5（°）/s之间；经指数趋近律法处理的算法能使稳定后俯仰角、俯仰角速度、偏航角、偏航角速度的振荡浮动分别处于±0.3°，±10（°）/s，±0.05°，±1.8（°）/s之间，且2种方法均能控制导弹命中目标点附近。证明经边界层法和指数趋近律法处理过后的滑模抖振问题，可以得到较好的抑制。

3.2 大扰动环境下仿真分析

高速动能弹飞行方式为贴地飞行，当脉冲发动机在低空中工作时，会引起周围气流发生强烈变化，由于弹体本身的高速度、大动能，气动系数偏高，流场的剧烈变化会产生较大的干扰力矩。

高速动能弹在高速飞行过程中，受到的干扰力矩变化快，范围波动大，测量难度较大。为验证弹体在大扰动力矩的影响下是否依旧能够命中目标：以纵向平面为例，对弹体纵向依次添加大小为0，50，80，100，120，130 N·m的脉冲干扰力矩，分别使用传统PID（proportional integral derivative）控制方法和本文所设计的滑模变结构制导控制算法对高速动能弹进行控制仿真。

假设目标坐标为（4 000，0）m，使用传统PID控制方法的弹体仿真结果如图16，17所示。

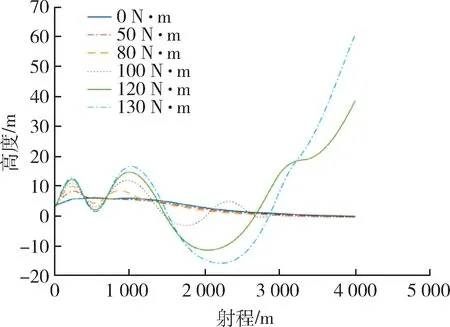
图16 导弹位置变化图Fig.16 Mission position change

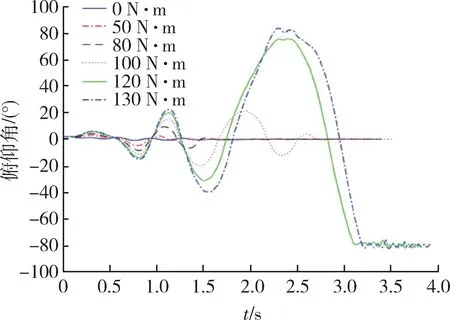
图17 俯仰角随时间的变化图Fig.17 Var iation of pitch angle with time

使用滑模变结构制导控制算法的弹体仿真结果如图18，19所示。

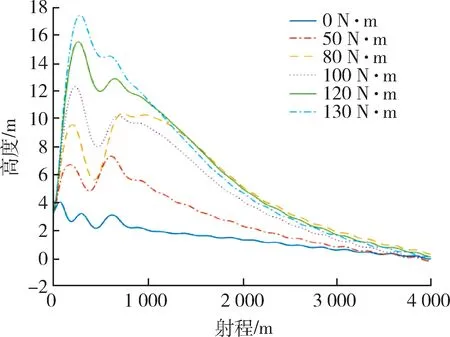
图18 弹体位置变化图Fig.18 Mission position change

对不同干扰力矩影响下的导弹落点进行整理，结果如表1所示。

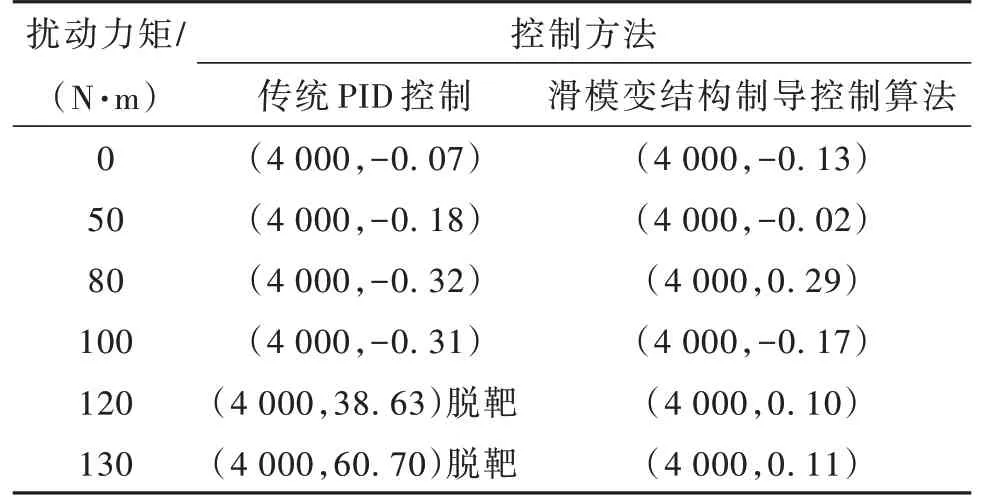
表1 导弹落点位置表Table1 Missile landing point coordinates m

观察比对以上数据可以发现，传统控制方法在不加干扰力矩及小力矩影响下，弹体可以很好地命中目标坐标。但随着扰动力矩增大，俯仰角的幅值变得越来越大，当扰动力矩达到120 N·m之后，会出现弹体失控、位置发散，导弹无法命中目标。反观使用滑模变结构算法控制的弹体，在加入相同大小的扰动力矩时，俯仰角最终都可稳定在1°以内；导弹落点均可命中目标坐标。

图19 俯仰角随时间的变化图Fig.19 Var iation of pitch angle with time

当高速动能弹以高速度在低空飞行时，会有剧烈的流场变化，产生强度较大的干扰力矩。相比于传统控制方法，本文设计的滑模变结构制导控制算法在大扰动力矩的干扰下精度更高，鲁棒性更强。故高速动能弹使用滑模变结构制导控制算法时控制效果更加出色。

4 结束语

本文推导出了一种新型基于滑模变结构的高速动能导弹制导控制算法，并对滑模变结构算法存在的固有抖振问题进行了相应处理。仿真结果表明，本文提出的新型制导控制算法能够控制弹体准确打击目标，经处理后的滑模抖振问题也能得到一定的削弱；且比传统方法在大力矩扰动情况下精度更高，具有一定的工程应用前景。