透波隐身机翼蒙皮设计参数优化方法仿真研究*

于天立，董文锋，刘文俭，范亚

（1.空军预警学院，湖北 武汉 430019；2.空军石家庄飞行学院，河北 石家庄 050051）

0 引言

雷达隐身技术作为飞行器隐身技术的重要组成部分，其实质就是雷达截面积减缩（radar cross section reduction，RCSR）技术。包括4种基本方法，即外形隐身技术、材料隐身技术、无源对消技术和有源对消技术，但最常用也是最有效的方法是前2种技术［1］。

外形隐身技术就是通过修改目标的外形几何特征，可以在一定角域范围内显著减小其雷达散射截面（radar cross section，RCS）的一种雷达隐身技术；材料隐身技术即利用材料对电磁波的通透性能、吸收性能及反射性能，实现降低RCS的目的［2-4］。但是，从外形隐身技术的机理来讲，某个角度范围内的RCS减缩必然伴随着另外一些角域内的RCS增加［5-6］，另外，为了满足飞行器气动方面的要求，由于外形减缩RCS的设计受到限制，再加上随着雷达波入射频率发生改变，可能会存在由于散射源谐振而导致RCS增加的风险，所以，仅仅依靠外形隐身技术有时尚达不到隐身指标的要求。因此，将外形隐身技术与材料隐身技术相结合是一种有效的方法［7］。机翼作为隐身飞机RCS的主要贡献部位，其散射源主要包括机翼表面爬行波、机翼前缘镜面反射、机翼尖顶绕射等。如何合理设计机翼外形，在有效减少机翼RCS贡献量的同时还能满足空气动力学性能的要求，成为了当今隐身飞机设计时一个必须攻克的难题。本文基于外形隐身技术与材料隐身技术相结合，提出一种以透波为主对机翼进行RCS减缩的机翼蒙皮设计方案。通过优化手段，在平衡机翼升力与电磁散射特性的基础上，确定透波机翼蒙皮外形几何特征，证明透波机翼在宽频带电磁波入射时隐身效能的有效性，并论证分析了透波机翼外形几何特征对机翼升力与电磁散射特性的影响。

1 机翼外形参数优化模型

设计优化的机翼可以看作是由一段较长的主翼加上一段较短的副翼构成的，外形俯视图如图1a）所示；翼面选用Clark-Y翼型，如图1b）所示。机翼蒙皮采用透波材料，蒙皮厚度为d，设透波材料为非磁性材料，μ=μ0，介电常数ε=εr+jεi，损耗角正切tanδ=εi/εr。

图1 机翼示意图Fig.1 Wing diagram

固定机翼蒙皮厚度d和电磁参数（μ，ε），对透波机翼外形的几何特征进行调整，通过仿真分析发现，机翼的RCS与升力都会随之发生改变。因此，希望经过精心的优化设计，来得到最好的隐身效果与最大升力并平衡二者之间的关系。

定义机翼弦长、第二弦长、第三弦长、半主翼展长、半副翼展长、机翼后掠角这6个机翼外形的几何特征为设计变量。

设飞机最大载重为t（单位：kg），重力加速度为g（单位m/s2）。以0.5，1.5，3 GHz 3个频点分别代表P，L，S 3个波段作为雷达波入射频率，入射方位角φ与俯仰角θ的定义如图2所示。应用Ansys Work‑bench软件里的CFX模块与FEKO软件对机翼分别进行空气动力学及RCS数值仿真，优化目标函数为透波机翼分别在3个波段入射时RCS均值的加权和最小。

图2 入射角示意图Fig.2 Schematic diagram of incidence angle

机翼外形特征优化问题的数学表达形式为

设计变量：x1，x2，x3，x4，x5，x6，

目标函数：

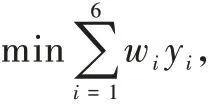
约束条件：

式中：x1，x2，x3，x4，x5，x6分别表示机翼弦长、第二弦长、第三弦长、半主翼展长、半副翼展长（单位：m）、机翼后掠角。考虑到目前飞行器隐身的难点主要在S波段以下，故着重研究这个频段。设计中取y1，y2，y3，y4，y5，y6，y7分别表示0.5 GHz频率入射时透波机翼在方位角范围内RCS的均值、0.5 GHz频率入射时透波机翼在俯仰角范围内RCS的均值、1.5 GHz频率入射时透波机翼在方位角范围内RCS的均值、1.5 GHz频率入射时透波机翼在俯仰角范围内RCS的均值、3 GHz频率入射时透波机翼在方位角范围内RCS的均值、3 GHz频率入射时透波机翼在俯仰角范围内RCS的均值（单位：dBm）、机翼的升力（单位：N）；wi为相应RCS的权重系数。

2 优化策略

由于机翼外形不规则、其几何特征对电磁散射与升力的影响存在一定的相关性，再加上优化计算量巨大、耗费时间长等原因，很难得到机翼外形几何特征参数的确定原则与规律。为克服上述困难，采用基于代理模型的优化方法［8-10］。基于代理模型的优化方法常被用于多学科设计优化，是指利用已知点的响应信息来预测未知点响应值的一类模型。其实质是以一个拟合精度和预测精度为约束，利用近似方法（approximation approaches）对离散数据进行拟合的数学模型。这类模型在数学上通过拟合与差值来实现，即利用已知点构造拟合函数来预测未知点响应或利用已知点信息插值计算未知点处的响应。基于代理模型的透波机翼几何参数优化方法流程如图3所示。

图3 基于代理模型的透波机翼几何参数优化方法流程图Fig.3 Flow chart of geometric parameter optimization method for wave transpar ent wing based on surrogate model

（1）生成样本方案。在第1节中已经确定了6个设计变量及其约束范围，即设计空间是确定的。对于数值仿真而言，均匀抽样与拉丁超立方抽样更可取一些［11］。拉丁超立方抽样是一种从多元参数分布中近似随机抽样的方法，属于分层抽样技术，具有抽样效率高、计算量小等优点。最优拉丁超立方抽样在保持分层抽样的同时改进了拉丁超立方抽样的均匀性，使所有的样本方案尽量均匀地分布在设计空间［12］。本文采用最优拉丁超立方抽样进行样本方案的生成，最优拉丁超立方抽样要求M≥(N+1)(N+2)/2，其中M为抽样点个数即样本方案个数，N为设计变量个数。为保证精度，本文使抽样点个数M=(N+1)(N+2)，其中N=6，生成56个样本方案。

（2）生成样本方案后，利用Ansys Workbench软件与FEKO软件对56个样本方案分别进行空气动力学及RCS数值仿真，输出每个样本方案所对应的升力与RCS数据。

（3）根据样本方案集与仿真结果，构造透波隐身机翼的代理模型。文献［13］详细介绍了代理模型的相关论述，一般常见的代理模型构建方法有径向基模型、神经网络、响应面模型、克里金模型等等。由于响应面模型具有系统性、使用性强，鲁棒性［14］良好，适用范围广且计算简单等优点，故采用响应面模型。

（4）代理模型构建完成后，需对其拟合度进行评判分析。均方根误差（root mean square error，RMSE）用来衡量预测值同真实值之间的偏差，对预测中的特大或特小误差反应非常敏感［15］。故采用将误差进行归一化处理的均方根误差分析法对代理模型的拟合精度进行分析，归一化后的RMSE表达式为

式中：L为归一化后的RMSE数值；n为误差分析点的总个数；Xact，i为第i个误差分析点的实际仿真值；Xpre，i为第i个误差分析点在代理模型上的预测值。根据L取值大小来判断模型拟合度的好坏，如果结果接近0，说明模型拟合效果很好，结果越大说明拟合效果越差，工程要求分析结果小于0.2。

（5）代理模型构建完毕后，为节约计算成本且获得全局最优解，在优化策略的选择时，本文采用多岛遗传算法的优化策略，在满足约束条件的前提下寻求最优解。

（6）优化得到最优解与最优参数后，将最优参数代入Ansys Workbench软件与FEKO软件对最优模型分别进行空气动力学及RCS数值仿真，输出最优模型的升力与RCS数值作为验证结果并与最优解作对比。

3 优化结果与分析

优化过程中在对模型进行升力及RCS数值仿真时，设蒙皮厚度d=1 mm，透波材料为非磁性材料，μ=μ0，介电常数取εr=3.55，tanδ=0.003；飞机最大载重t=1 000 kg，重力加速度g=9.8 m/s2，飞行速度v=220 m/s；在进行RCS数值仿真时，采用FEKO自带的MOM算法，方位角φ与俯仰角θ的入射范围分别为（0°，40°）与（-20°，20°），步长为1°；6个权重系数（wi，i=1，2，3，4，5，6）均为1/6。应用以上优化策略对透波机翼蒙皮进行外形优化。

代理模型拟合度分析时，取误差分析点数n=20，代理模型预测值与样本方案测量值的线性回归关系如图4所示。

图4 代理模型预测值与样本方案测量值的线性回归关系图Fig.4 Linear regression relationship between the predicted value of surrogate model and the measured value of sample scheme

归一化后的均方根误差分析如表1所示，可以看出，7个目标变量的代理模型偏差均小于0.2，模型拟合度较高，可供工程使用。

表1 归一化后的均方根误差分析表Table1 Root mean squar e er ror analysis after nor malization

优化后的设计变量参数取值如表2所示。

表2 优化后设计变量取值表Table2 Values of variables after optimization

将优化后的设计变量参数输入透波机翼模型中，利用FEKO软件对透波机翼蒙皮进行RCS数据仿真得到验证结果，将得到的优化结果与验证结果进行对比，如表3所示。

从表3可以看出，仅在0.5 GHz频率入射时俯仰角范围内的RCS差值达到3 d Bsm，其余结果差值均在2 d Bsm以内，升力差值90.9 N，优化结果与验证结果相比较数值差别较小，与代理模型拟合时的误差分析结果相吻合，进一步证明了代理模型的可信度与有效性。

表3 优化结果与验证结果对比表Table3 Comparison of optimization results and verification results

将优化后的设计变量参数输入金属机翼模型中，利用FEKO软件对同外形几何特征参数的金属机翼进行RCS数据仿真，将代理模型得到的RCS优化结果与金属机翼RCS仿真数据对比，如表4所示。

从表4可以看出，当以P，L，S 3个波段入射时，无论是俯仰角还是方位角的入射范围内，透波蒙皮的RCS都远小于金属机翼。

表4 优化结果与金属机翼RCS仿真数据对比表Table4 Comparison between optimization results and RCSsimulation data of metal wing

通过仿真发现，在入射方位面或俯仰面范围内，目标变量与设计变量之间RCS的变化趋势随频率改变而发生的改变很小。故以0.5 GHz频率为例，做RCS与升力的趋势变化图，如图5，6所示。

（1）入射波方位角对RCS的影响

由图5可以看出，电磁波入射俯仰角保持0°不变，改变入射方位角时，透波机翼的RCS均值受机翼弦长、第二弦长与机翼后掠角度影响较大。其变化趋势为，在透波机翼其他外形特征保持不变的情况下：①透波机翼的RCS随后掠角度的增大先变大后变小，并在25°附近达到最大值，如图7所示。这是由于反射电磁波同样存在旁瓣，当机翼后掠度较小时，以较大的方位角度入射时所接收到的反射电磁波辐射场强度较小；当机翼后掠度较大时，以较小的方位入射角度入射时所接收到的反射电磁波辐射场强度较小；当机翼后掠度适中时，0°～40°的方位入射角范围内入射方向所接收到的反射电磁波辐射场总强度较大，从而此入射范围内的均值RCS较大。②当机翼弦长增加时，电磁波所照射的投影区域面积增大，故透波机翼的RCS随机翼弦长的增大而增加，如图8所示。③透波机翼的RCS随第二弦长的增大而增加，如图5所示。

图7 0.5 GHz频率时方位角入射范围内RCS与后掠角度的关系Fig.7 Relationship between RCSand sweep angle in azimuth incidence range at 0.5 GHz

图8 0.5 GHz频率时方位角入射范围内RCS与机翼弦长的关系Fig.8 Relationship between RCSand wing chord length in azimuth incidence range at 0.5 GHz

（2）入射波俯仰角对RCS的影响

入射方位角保持0°不变，改变电磁波入射俯仰角时，透波机翼的RCS均值受机翼弦长、第二弦长与机翼后掠角度影响较大。其变化趋势为，在透波机翼其他外形特征保持不变的情况下：①随着机翼后掠角的增加，镜面反射效应越来越弱，故俯仰角上透波机翼的RCS随透波机翼后掠角度的增大而减小，且随着角度的增加入射方向所接收到的旁瓣越来越小，旁瓣差值变小，故RCS减量变小，如图9所示。②受照射投影区域变大的影响，透波机翼的RCS随透波机翼弦长与第二弦长的增大而增大，如图5所示。

图5 0.5GHz频率时设计变量与RCS的关系Fig.5 Relationship between design variables and RCSat 0.5GHz

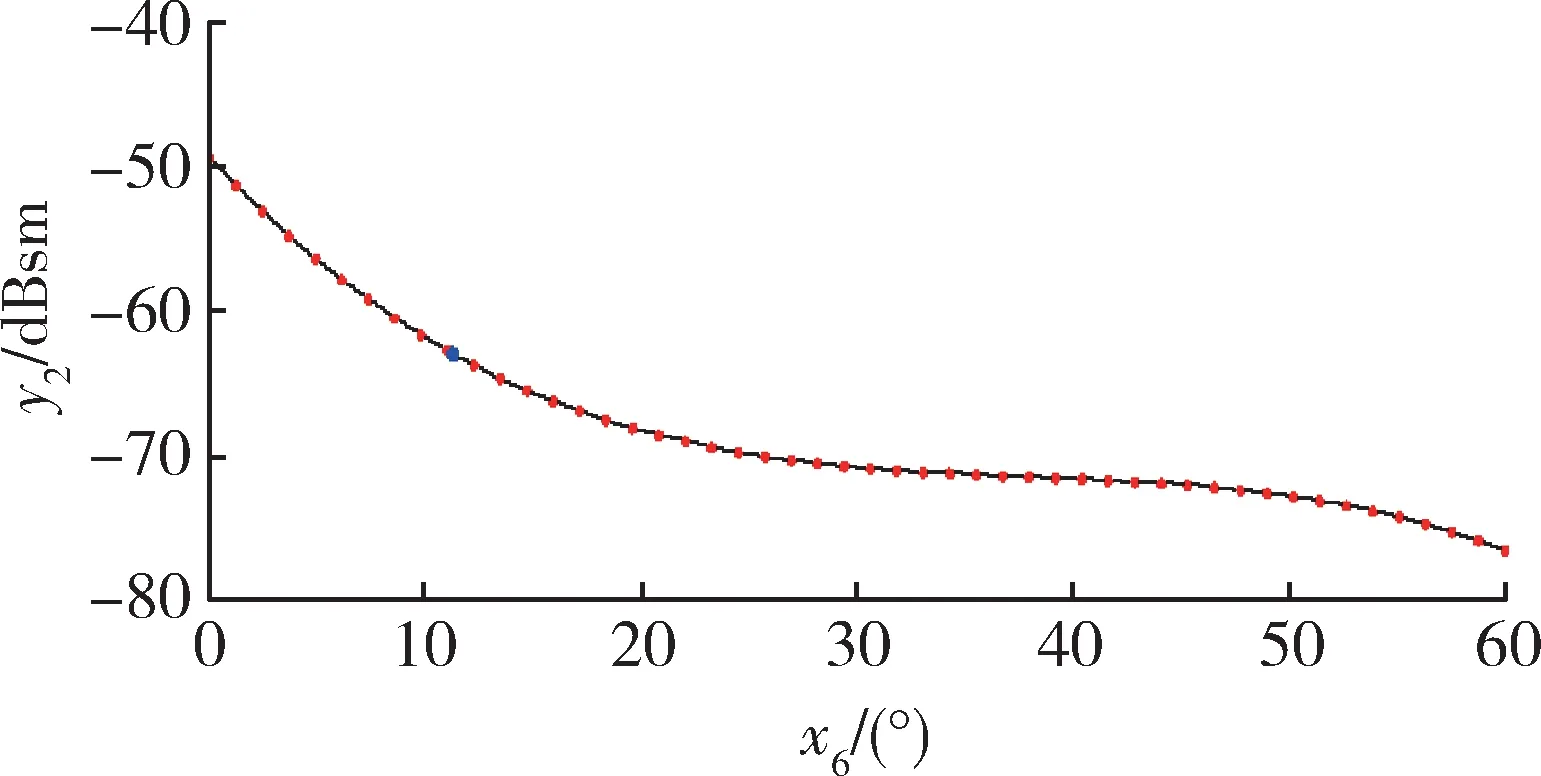
图9 0.5 GHz频率时俯仰角入射范围内RCS与后掠角度的关系Fig.9 Relationship between RCSand sweep angle at 0.5 GHz

（3）对机翼升力的影响

①从图6可以看出，受伯努利原理与机翼升力面积所影响，透波机翼的升力随机翼弦长、第二弦长、第三弦长、半主翼展长、半副翼展长的增加而增加，随着透波机翼后掠角度的增加而减小；其中，受半主翼展长与机翼后掠角度的影响程度最大。②半主翼展长与机翼后掠角度在对机翼升力的影响上存在一定的相关性，随着机翼后掠角度的增大，机翼升力随半主翼展长增大而变大的增量变小，如图10 a）所示。③半主翼展长与机翼弦长在对机翼升力的影响上存在一定的相关性，即随着机翼弦长的增加，机翼升力随半主翼展长增大而变大的增量变大，如图10 b）所示。

图6 升力与设计变量的关系Fig.6 Relationship between lift and design var iables

图10 机翼升力与设计变量的关系云图Fig.10 Relationship between wing lift and design variables

4 结束语

对飞机机翼隐身设计来说，在满足升力约束条件的前提下，应尽可能多地对俯仰与方位范围内的RCS进行减缩。为确定透波隐身机翼外形几何特征参数，应用了一种基于代理模型构建的优化策略，这种优化策略具备耗时少、计算量小、平衡跨学科领域问题的同时还可以进行参数特性分析等优点。经过优化后可以发现，相比于金属机翼，无论是考虑空间范围还是频域范围，透波机翼蒙皮都具有巨大的RCS减缩空间，这为下一步考虑透波材料力学性能后，在透波机翼内部增加梁、肋设计提供了一定的操作空间，因为这些内部结构可能会带来附加的RCS增量。然而，即使增加了内部结构，本文中的优化设计方法也仍然是有效的。