基于数学核心素养的高中数学教学设计
胡娜 王晓 杨静宇





摘 要:《普通高中课程标准(2017年版)》的颁布与实施,切实推动了高中教育阶段数学课程教学进行全方位的改革。新课标实施以来,数学的教学过程逐步从“灌输式”向“启发式”和“体验式”转变。如何在教学过程中将数学核心素养融会其中成为研究热点。本文基于核心素养的理念,以三角函数的性质课程教学设计为例,探索高中数学课程的教学设计。
关键词:核心素养;教学设计;三角函数
中图分类号:G633.6 文献标识码:A 文章编号:1673-260X(2022)04-0018-02
1 引言
我国的教育改革自20世纪70年代以来从未间断过。特别是在2005年,联合国教科文组织对基础教育的教学质量问题进行了系统地研究,明确了基础教育的教学质量体系与框架[1]。党的十八大召开后,在教育改革的过程中,教育部明确提出发展学生的核心素养[2],这也是核心素养首次出现在大众的视野。立德树人培养民族复兴的时代接班人,离不开新思想下的核心素养教育,离不开以核心素养为导线的教学方法。以核心素养为导向的教学模式相关的教育理论一经面世,便引起了教育专家和一线教师的广泛关注,也成为当前国内各学科教学领域的研究热点。
关于数学核心素养,马云鹏[3]认为数学核心素养不仅培养了学生的数学思维方式,还提升了学生学习数学的数学精神和数学文化知识。史宁中教授[4]指出,数学核心素养是数学的基本特质,关系着每个个体在终身发展中的思维品质和在社会发展中应具备的能力。在《普通高中数学课程标准(2017年版)》中,数学核心素养的六方面内容是数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析[5]。在数学学习过程中,学习者的数学核心素养应该具备适应自己终身发展和社会发展中所必需的数学品格以及掌握数学关键能力[6]。
如果说数学课程目标的聚焦点在于数学核心素养,那么实现课程目标的前提和重要基础理所当然是教学设计。教学设计是通过程序化步骤来分析教与学问题的过程,是教师教学过程的引导线,是教学预设与生成的核心枢纽。在新课标中的“以学生发展为本,立德树人,提升素质”等理念,对数学核心素养下教师的教学设计具有推动作用。如何在课堂上让数学核心素养落地生根,这需要教师在课前做合理的教学设计。
2 基于数学核心素养的教学设计
本文以数学核心素养为导向,给出人教A版“三角函数的性质”的教学设计。
2.1 教学目标
(1)根据y=sinx,y=cosx的图像,掌握其定义域、值域、单调性等性质的推导过程,应用性质解决实际问题。
(2)通过讨论交流、探究y=sinx,y=cosx的图像,加深对于其性质的理解,从而提升抽象概括的能力,体会数形结合、转化与化归的思想。
(3)通过本节课,学生学习数学的兴趣得以提高,培养学生合作意识与探索兴趣。
2.2 教学过程
(1)复习引入
教师通过PPT要求学生根据所学的内容,独立画出y=sinx,y=cosx的图像;学生完成老师的留下的作业;教师巡查学生的完成效果,评价后并引出本节课的教学主题,即正余弦函数的性质。
设计意图:通过对y=sinx,y=cosx图像的复习,有利于检验学生对y=sinx,y=cosx图像的掌握情况,同时为本节课的教学内容打下扎实的基础。
(2)新课讲授
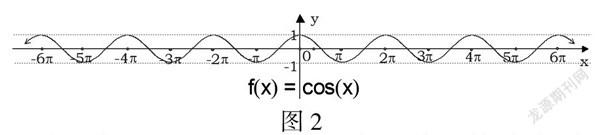
教师用课件展示y=sinx,y=cosx的图像,如图1和图2所示,请学生进行组内探究合作,在规定时间内解决问题。
问题一:y=sinx,y=cosx的定义域、值域分别是什么?
问题二:你能依据图像找出y=sinx,y=cosx的周期吗?
由函数图像可知,y=sinx,y=cosx的定義域都是(-∞,+∞),即R;在y=sinx中x=+2k?仔时,ymax=1;当x=-+2k?仔时,ymin=-1;y=cosx中,当x=0+2k?仔时ymax=1;当x=?仔+2k?仔时,ymin=-1,故值域都为[-1,1];其周期都为2?仔。
教师针对学生的回答,给予鼓励与评析,并对函数的周期性进行详细地讲解,由sinx=sin(x+2?仔),cosx=cos(x+2?仔),则正余弦函数的周期都为2?仔,也为最小正周期。
设计意图:利用多媒体直观地展示问题,营造轻松的学习氛围,有助于促进学生的合作交流,吸引学生的注意力。
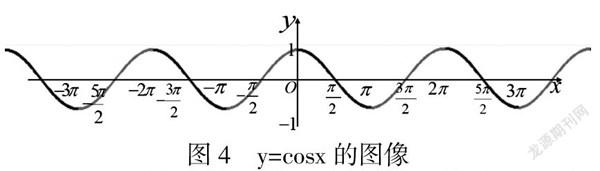
教师请同学们依据所学知识及函数图像,判断并计算y=sinx,y=cosx的奇偶性,且找出其单调递增、递减区间,如图3和图4所示。
方法一:由函数图像可知,奇函数关于原点对称,偶函数关于y轴对称;方法二:若存在函数f(x),当f(-x)=-f(x),f(x)为奇函数,当f(-x)=f(x),f(x)为偶函数。经计算,y=sinx为奇函数,y=cosx为偶函数。
y=sinx在闭区间[-+2k?仔,+2k?仔](k∈Z)单调递增,在闭区间[+2k?仔,+2k?仔](k∈Z)单调递减;y=cosx在[2k?仔-?仔,2k?仔](k∈Z)单调递增,在闭区间[2k?仔,2k?仔+?仔](k∈Z)单调递减。
设计意图:通过提问和引导学生思考问题,不仅体现了教师是教学过程的引导者,将课堂交给学生探索发现并解决问题,而且有利于学生快速获取知识,远大于教师直接讲课的效果。
(3)巩固练习
教师通过多媒体展示正余弦函数性质不同类型、层次的题目。
例1 计算下列函数的定义域和值域。
(1)y= (2)y=3-sinx
例2 计算函数y=sin6x的最小正周期。
例3 计算函数y=2cos3x的单调区间。
教师安排学生代表到黑板上做题,其余同学在演草纸上写,完成后教师对学生的做题情况,进行评析并总结。
设计意图:设置阶梯形的题目,思维层次不同的学生能力都能得到锻炼,对学生的表现及时评价,不仅能激励学生,还能增进师生间的交流。
(4)课堂总结
教师引导学生从y=sinx,y=cosx的图像出发、从图像中一步步归纳总结y=sinx,y=cosx的性质,说出具体的共同点和区别,并总结自己在本节课的收获。
通过学生独立思考和小组间的讨论,教师或学生对学生的回答给予评价。
设计意图:教师和学生在一起总结的方法,可检验学生对本节课知识的认知,进一步增强学生对学习数学的自信心,从而更加热爱数学。
(5)课后作业
画图表整理正弦、余弦函数的性质;完成配套练习。
设计意图:加深、巩固学生对知识的理解,培养学生勤于总结知识的习惯。
3 总结
在立足高中数学课堂实践的基础上,本文通过对三角函数部分内容进行教学设计,进一步探索在数学核心素养下高中数学课程教学设计模式,其目的是在数学核心素养、数學基本思想、基本能力与教学实践的交融中,使核心素养下的教学设计能落地生根,并抓住其生成点和发展点,为高中数学的教学探索一条适合的路径。
——————————
参考文献:
〔1〕董建红.联合国教科文组织教育质量框架探析[J].教育发展研究,2007,28(21):19-22.
〔2〕全面深化课程改革落实立德树人根本任务[N].中国教育报,2014-06-23(008).
〔3〕马云鹏.关于数学核心素养的几个问题[J].课程.教材.教法,2015,35(09):36-39.
〔4〕史宁中.学科核心素养的培养与教学[J].中小学管理,2017,31(01):35-37.
〔5〕中华人民共和国教育部制订.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018.
〔6〕孔凡哲.数学学科核心素养:为什么、是什么[J].湖北教育(教育教学),2020,71(03):38-40.
收稿日期:2021-12-19
通讯作者:杨静宇,教授,博士,硕士生导师,研究方向:函数空间上的算子理论,数学教育。
基金项目:赤峰学院教育教学研究项目(JYXMY202114)

