基于多案例统计的基坑开挖引起的下卧既有隧道隆起量预测公式及其工程应用

刘波，章定文，杨文辉，李星

(1. 东南大学土木工程学院，江苏南京，211189；2. 东南大学未来地下空间研究院，江苏南京，211189；3. 东南大学交通学院，江苏南京，211189)

近年来，随着城市轨道交通和地下空间开发的迅速发展，在既有隧道上方进行基坑开挖的现象日益增多[1]。开挖卸荷将不可避免地引起坑底及其下部一定深度范围内的土体回弹，进而导致埋置于其中的隧道变形。目前，学者们采用多种方法对基坑开挖引起的下卧隧道响应进行了研究。在理论解析方面，刘国彬等[2]根据大量的实测资料，提出了一种基于残余应力原理和应力路径方法建立的基坑坑底隆起变形计算模型。张治国等[3]首先根据Mindlin 解计算开挖卸荷引起的土中附加应力，再将隧道简化为Winkler弹性地基上的无限长梁，推导出了隧道受基坑开挖影响的纵向受力变形解析解。为解决Winkler地基模型不能考虑土弹簧间的相互作用的问题，LIANG 等[4-6]采用Pasternak 地基模型分析土体和隧道之间的相互作用。在此基础上，康成等[7]则提出了一种非线性Pasternak 地基模型，用以反映地基变形和地基反力之间的非线性特征。在数值模拟方面，黄宏伟等[8]以外滩通道上跨延安东路大直径越江隧道为背景，计算分析了开挖引起的下卧隧道变形，评价了土体加固和坑底堆载对隧道的保护效果。郑刚等[9]对某上跨地铁箱体隧道的基坑施工过程进行了动态模拟，分析了隧道两侧土体加固、底板浇筑、抗浮桩、堆载回压等措施对下卧箱体轨道的影响和控制效果，认为综合采用这些措施可有效控制下卧箱体隧道的上抬变形。在模型试验方面，NG等[10-11]开展了砂性地层中地下室基坑开挖对下卧隧道影响的系列离心模型试验，分析了砂的密度对隧道响应的影响，发现下卧隧道截面发生了竖向拉长、横向压缩的变形，且当砂的密度降低25%时，隧道拉应变增加20%。HUANG等[12]开展了软黏土地层中明挖通道基坑开挖对下卧隧道影响的系列离心模型试验，发现开挖引起下卧隧道隆起的范围约为基坑开挖宽度的2.5倍，隧道纵向隆起可以用高斯曲线进行拟合。

现场实测法可直观地揭示开挖影响机理，得到所有影响因素的综合作用结果，是研究该类问题的有效方法。例如，CHEN 等[13-16]分别对上海、杭州、天津、广州等不同城市地层中下卧隧道受基坑开挖影响的变形特性进行了测量分析。然而，目前研究大多针对具体案例，而每个案例都有其特殊性和唯一性(如地层条件、开挖与隧道的相互位置关系、施工工艺等)，故所得到的结论往往也仅适用于该特定案例，对类似工程的指导作用有限。

为此，本文作者广泛调研国内基坑开挖对下卧既有隧道影响的工程案例，根据案例所处典型地层条件，将案例划分为3类，每类案例中统计基坑和隧道的尺寸、相对位置、结构变形以及控制方法等。根据统计数据，分析案例所处地域及地层分布情况、基坑和隧道形式及尺寸分布情况、基坑和隧道相互位置关系以及隧道隆起控制措施等，分析地层条件、基坑形式、基坑开挖深度、开挖面积、卸荷率以及隧道穿越基坑实际长度等对隧道隆起量的影响。在此基础上，提出隧道隆起量预测指标，建立隧道隆起变形与影响因素之间的内在联系，给出不同地层条件下隧道隆起量预测公式。最后，依托具体工程实例，利用得到的预测公式对基坑开挖前的隧道隆起量进行预测，开挖过程中对隧道隆起量进行现场实时监测，并将预测结果与实测结果进行对比，验证本文所提预测公式的合理性。

1 工程案例调研与统计分析

1.1 工程案例调研

为了分析基坑开挖引起的下卧隧道隆起变形特性以及各因素对变形的影响，在此基础上形成隧道隆起量实用性预测方法，通过文献调研对国内33 个工程案例、共计48 条隧道进行归纳统计，结果见表1[17]。

基坑和下卧隧道尺寸、相对位置关系及结构变形示意图见图1。图1 中，a为基坑横向开挖长度；b为基坑纵向开挖长度；l为隧道实际穿越基坑长度；α为隧道与基坑水平夹角；R为隧道外径；He为基坑开挖深度；Ht为隧道拱顶与坑底距离；H为基坑开挖前隧道拱顶初始覆土厚度；Smax为隧道最大隆起量。

1.2 工程案例统计分析

1.2.1 案例所在地区及典型地层条件

由表1 可见：绝大多数案例位于上海、杭州、南京等东南沿海地区，其中仅上海地区案例占比达51.5%，少数案例位于中西部地区。这可能是因为东南沿海地区经济发展水平高，地铁建设起步早、运营里程长，且地下空间开发利用程度高，因此出现了较多的基坑开挖引起的隧道变形问题，而中西部地区经济发展水平相对较低，地铁建设起步晚、运营里程短，地下空间开发利用程度较低，因此此类问题相对较少。

根据案例所处典型地层的不同，将表1中的案例划分为3类。案例1～20为第1类，主要位于软黏土地层中，约占案例总数的60.6%；案例21～26 为第2 类，主要位于粉土-粉砂性地层中，约占总数的18.2%；案例27～33为第3类，主要位于砂卵石-风化岩地层中，约占案例总数的21.2%。下面分析地层条件对隧道隆起变形的影响，并推导出这3类地层条件下的隧道隆起量预测公式。

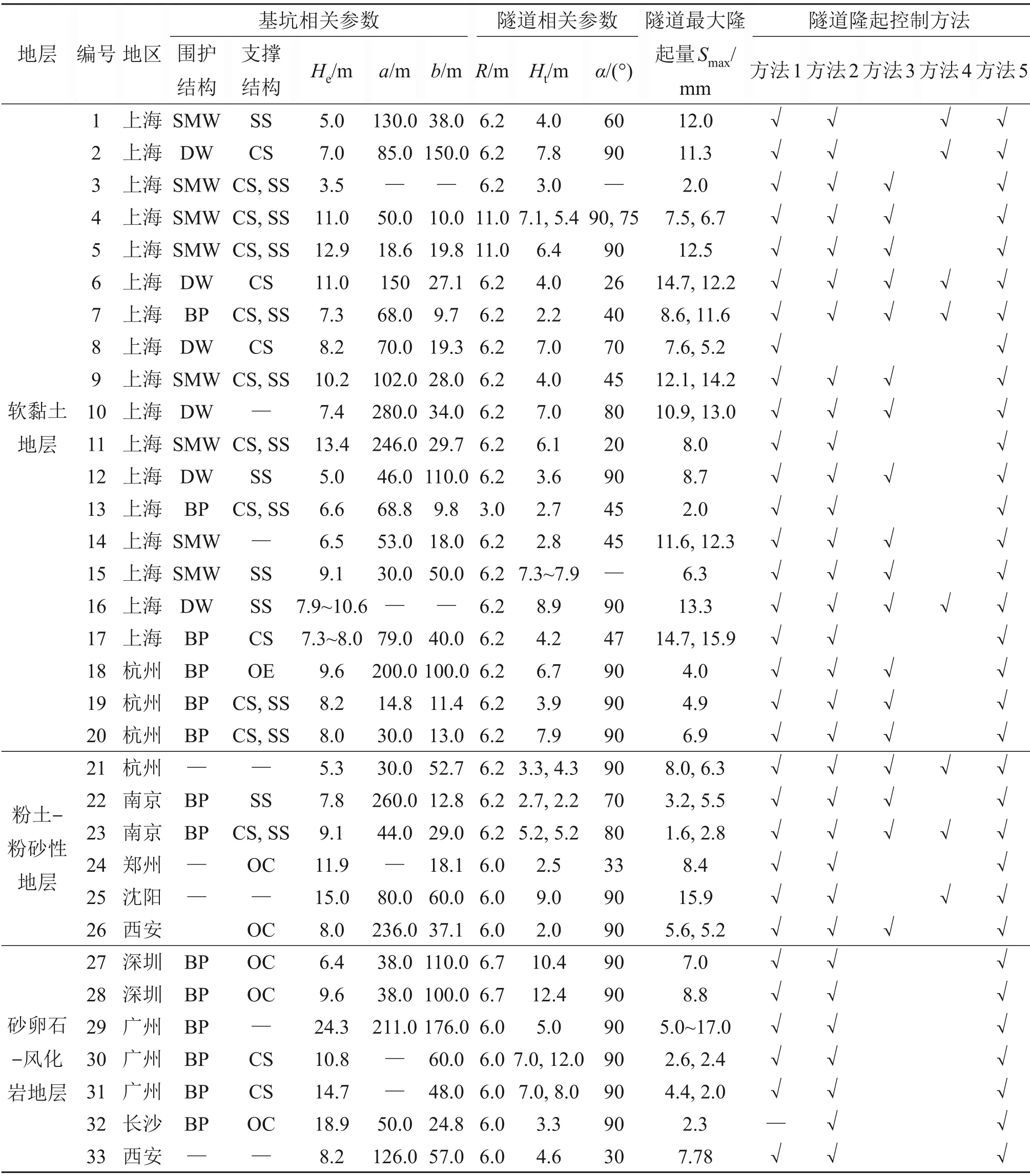
表1 基坑开挖对下卧隧道影响的案例统计[17]Table 1 Case statistics of influence of deep excavation on existing underlying tunnel[17]

1.2.2 基坑和下卧隧道形式及尺寸

在各个案例中，基坑主要分为明挖通道和地下室(或广场)2 类，其中明挖通道占比约60.6%。地下室(或广场)虽然数量相对较少，但由于开挖面积大、开挖深度深，卸荷效应相对明挖通道基坑更加明显，对下卧既有隧道的影响更大，因此也不容忽视。

图2 所示为基坑开挖深度He统计直方图。由图2 可见，He分布范围为3～27 m，其中，He为6～9 m的基坑所占比例最大；He≤9 m的基坑约占总数的51.5%；He≤12 m的基坑约占总数的81.8%；He≤15 m的基坑约占总数的90.9%；He≤18 m的基坑约占总数的93.9%。

案例中，基坑围护结构形式主要有SMW(soil mixing wall)工法桩、钻孔灌注桩、地下连续墙等。其中，因地下通道基坑开挖深度相对较浅，SMW工法桩和钻孔灌注桩的应用最广泛。坑内支撑结构形式主要有钢管支撑和钢筋混凝土支撑2种。对于土层性质较差的软黏土地层中的基坑，均采用坑内支撑；对于土层性质较好的砂质、岩质地层中的一些基坑，未采用坑内支撑而直接采用放坡明挖。

案例中，下卧隧道结构形式为城市地铁盾构圆形隧道，隧道直径通常为6.0 m 或6.2 m。因此，本文不再分析隧道结构形式对隧道隆起变形特性的影响。

由前述案例分析可知，目前针对基坑开挖对下卧既有隧道影响的研究多集中于软弱土地层中围护墙(桩)+内撑式明挖通道基坑开挖对城市地铁盾构隧道的影响。

1.2.3 基坑和下卧隧道相互位置关系

图3所示为下卧隧道拱顶距坑底竖向距离Ht与开挖深度He之比(Ht/He)的统计直方图。由图3 可见：Ht/He分布范围为0～1.8，其中，Ht/He为0.4～0.6 的隧道所占比例最大，Ht/He≤1.0 的隧道约占隧道总数的91.7%，即绝大多数隧道埋深均位于坑底以下1倍开挖深度范围内。

1.2.4 下卧隧道变形控制措施

由表1可知：工程中常用的下卧隧道变形控制方法包括土体加固、分层分区施工、抗拔桩、坑底压重抗浮以及现场监测等。

图4所示为下卧隧道变形控制方法的统计直方图。由图4 可见：几乎所有案例都采用了土体加固、分层分区开挖以及现场监测这3种方法。在软黏土地层中，70%的案例采用抗拔桩方法，25%的案例采用坑底压重抗浮方法；在粉土-粉砂性地层中，66.7%的案例采用抗拔桩方法，50.0%的案例采用压重抗浮方法；在砂卵石-风化岩地层中，所有案例均未采用抗拔桩和坑底压重抗浮方法。

由此可见，软黏土和粉土-粉砂性地层中采用的隧道变形控制方法较相近且数量较多，而砂卵石-风化岩地层中采用的隧道变形控制方法的数量较少。

2 下卧隧道竖向位移影响因素分析

由基坑开挖对下卧既有隧道的影响机理可知，隧道受竖向开挖卸荷影响，竖向位移远大于水平位移，是隧道变形控制的关键。因此，下面重点探讨各影响因素对隧道竖向位移的影响。

2.1 地层条件的影响

图5 所示为不同地层条件下隧道最大隆起量(Smax)与基坑开挖深度(He)的关系。由图5可见：在软黏土地层中，Smax=(0.31‰～2.40‰)He，平均值为1.19‰He；在粉土-粉砂性地层中，Smax=(0.18‰～2.38‰)He，平均值为0.92‰He；在砂卵石-风化岩地 层 中，Smax= (0.04‰～1.09‰)He，平均值为0.42‰He。3 类地层中，Smax的平均值按从大到小顺序排列依次为软黏土地层、粉土-粉砂性地层、砂卵石-风化岩地层，前者地层中Smax平均值分别为后两者地层中Smax平均值的1.3倍和2.8倍。由此可见，地层条件对基坑开挖引起的隧道隆起量有显著影响。

此外，由图5还可以看出，即使处于同一种地层，Smax的变化范围仍然很大。软黏土地层、粉土-粉砂性地层、砂卵石-风化岩地层中，Smax的上、下限值之比分别为7.75，13.53 和28.43，Smax与单因素He之间的相关性很弱。

2.2 基坑形式的影响

明挖通道基坑平面一般呈长条形，开挖深度也相对较浅，而地下室(或广场)基坑平面一般呈矩形或多边形，开挖面积较大，开挖深度也较深，因此两者在开挖卸荷效应上也存在一定差异。

图6 所示为不同基坑形式下隧道最大隆起量(Smax)与基坑开挖深度(He)的关系。由图6可见，明挖通道基坑开挖引起的Smax=(0.04‰～2.38‰)He，平均值为0.88‰He；地下室(或广场)基坑开挖引起的Smax=(0.14‰～2.4‰)He，平均值为1.04‰He。地下室(或广场)基坑开挖引起的Smax平均值约为明挖通道基坑开挖引起的Smax平均值的1.2倍。由此可见，工程中地下室(或广场)开挖对下卧隧道的影响比明挖通道基坑的影响更大。

在相同基坑形式下，Smax的变化范围仍然非常大。明挖通道和地下室(或广场)基坑开挖时，Smax上、下限值之比分别为61.8 和17.6，Smax与单因素He之间无明显相关性。

2.3 基坑开挖卸载率的影响

基坑开挖竖向卸荷引起的坑底回弹是下卧隧道隆起变形的主要原因。魏纲[18]采用卸载率即基坑开挖深度与隧道初始覆土深度之比来描述卸荷程度，其取值范围为0～1。理论上讲，卸载率越大说明隧道距坑底越近，开挖卸荷越彻底，对下卧隧道的影响越显著。

图7 所示为不同地层条件下隧道最大隆起量(Smax)与卸载率(He/H)关系。由图7可见：在软黏土地 层 中，He/H为0.47～0.77，Smax=(2.86～25.30)He/H，平均值为15.61He/H；在粉土-粉砂性地层中，He/H为0.52～0.94，Smax=(2.51～25.49)He/H，平均值为10.45He/H；在砂卵石-风化岩地层中，He/H为0.38～0.91，Smax=(0.75～20.50)He/H，平均值为7.53He/H。3 类地层中，He/H变化范围按从大到小顺序排列依次为砂卵石-风化岩地层、粉土-粉砂性地层、软黏土地层；相反地，Smax平均值按从大到小顺序排列依次为软黏土地层、粉土-粉砂性地层、砂卵石-风化岩地层。这说明对于工程性质较好的地层，基坑开挖深度较深，卸载更加充分，但对埋置其中的隧道变形影响却很小。

由图7 还可以看出，不同地层中Smax的变化范围很大。在软黏土地层、粉土-粉砂性地层和砂卵石-风化岩地层中，Smax的上、下限值之比分别为8.84，10.17 和27.33，Smax与单因素He/H之间无明显相关性。

2.4 基坑开挖面积的影响

当基坑纵向开挖长度一致时，基坑沿隧道横向开挖长度越大，即基坑开挖面积越大，卸荷效应越显著，因此基坑开挖面积也是影响下卧隧道隆起的因素之一。

图8 所示为隧道最大隆起量(Smax)与基坑开挖面积(A，A=ab)的关系。由图8 可见：在实际工程中基坑开挖面积变化范围很大，软黏土地层和粉土-粉砂性地层中基坑开挖面积基本在15 000 m2范围内，而砂卵石-风化岩地层中基坑面积有的高达40 000 m2。总体上，Smax随着A增大呈增大趋势，但相对于A而言，Smax的增幅有限，造成数据离散性强，因此仅根据基坑开挖面积对隧道隆起量进行预测将会产生较大误差。

2.5 隧道穿越基坑长度的影响

当隧道穿越矩形基坑时，基坑与隧道纵向垂直的围护结构会对隧道两端产生约束作用而限制其隆起变形，基坑沿隧道纵向长度决定了隧道实际穿越长度和受开挖影响的范围，因此基坑沿隧道纵向的开挖长度(b)是影响隧道隆起的重要因素。隧道的实际穿越长度(l)可由基坑沿隧道纵向开挖长度(b)以及隧道水平夹角(α)通过公式l=b/sinα进行计算。

图9 所示为不同地层中隧道最大隆起量(Smax)与实际穿越长度(l)关系。由图9可见：随着l增大，Smax总体上呈增大趋势，其中软黏土地层和粉土-粉砂性地层中Smax随l的增幅大于砂卵石-风化岩地层中Smax的增幅，但数据较离散，Smax与单因素l之间未见明显相关性。

3 下卧隧道隆起量预测公式

3.1 现有预测公式及存在的问题

基坑竖向卸荷引起的下卧隧道隆起涉及的影响因素较多，使得合理预测开挖引起的隧道最大隆起量的过程变得非常复杂。由前文分析可知，虽然隧道最大隆起量(Smax)随着基坑开挖深度(He)、隧道穿越基坑长度(l)以及基坑卸载率(He/H)增加有增大的趋势，然而各因素之间未见明显相关性。因此，要想科学地预测基坑竖向开挖卸荷引起的下卧隧道隆起，必须综合考虑多种因素的影响，而不能只考虑单一因素。

魏纲[18]认为基坑开挖卸荷引起的下卧隧道隆起主要与以下因素有关：1)基坑开挖深度h、隧道顶部初始覆土厚度H，并采用卸载率N=h/H表征卸荷程度；2)基坑开挖暴露的隧道长度B，沿隧道纵向暴露的长度越长，卸荷的影响程度越大。定义(BN)为基坑的相对开挖长度，由卸载率计算公式可得BN=Bh/H，其值越大说明基坑开挖对隧道的影响越大。综合上述影响因素，提出了隧道最大隆起量预测模型[18]：

式中：f1和f2为与施工控制条件有关的变量，可通过工程实例拟合得到。

魏纲[18]提出的模型为预测基坑竖向开挖卸荷引起的隧道隆起量提供了良好的思路，然而该模型是在总结上海软黏土地层案例的基础上得到的，未考虑其他地层条件的影响。

陈仁朋等[19]基于魏纲[18]提出的卸载率的概念，统计了隧道纵向不同断面的卸载率与隧道隆起量，发现实际工程条件下隧道隆起量与卸载率存在良好的线性关系，这可能是因为坑底搅拌桩加固使得隧道周围土体的强度和刚度有所提高，在基坑开挖过程中，加固后土体回弹变形以弹性为主，回弹量取决于隧道上方应力释放程度。然而，本文作者对多个案例进行统计分析，并未发现隧道隆起量与卸载率之间存在线性关系。因此，并不能通过卸载率这一单一因素对隧道隆起量进行预测。

郭鹏飞等[20]在考虑卸载率(N)的基础上，通过对基坑开挖面积A取对数(lgA)来考虑基坑面积的影响，并引入形状因子来考虑基坑形状的影响。综合分析各影响因素，提出了隧道最大隆起量Smax的预测模型[20]：

该模型的形式与式(1)基本一致，但将隧道暴露长度(B)的影响变更为基坑开挖面积(A)的影响，在考虑卸载率(N)的基础上同时考虑了基坑形状的影响，然而这3个影响因素均为基坑相关的因素，未考虑隧道相关的因素。

3.2 本文预测公式

本文提出的隧道最大隆起量(Smax)预测公式拟考虑的影响因素包括工程地质条件、基坑开挖卸载率和隧道穿越基坑长度，影响因素涵盖了地层、基坑和隧道3个方面。其中，工程地质条件的影响根据案例所处地层来考虑；开挖卸载率(He/H)采用魏纲[18]提出的公式；隧道穿越基坑长度(l)通过基坑纵向开挖长度(b)和隧道与基坑水平夹角(α)计算获得，对于非规则形状基坑，根据实际情况确定。

因统计的隧道结构形式为城市地铁盾构隧道，直径均在6.0 m 或6.2 m 左右，因此隧道形式的影响不通过具体参数体现。地基加固、分层分区开挖、抗拔桩等施工控制措施的影响已包含在实测结果中，因此也不通过具体参数体现。

根据第2 节分析结果，采用lHe/H作为隧道隆起量综合预测指标，该指标值越大说明竖向卸荷对下卧隧道的影响越大。对于包含双线隧道的案例，Smax取上、下行线(或左、右线)最大隆起量的平均值，以减少同一案例中双线隧道隆起量不同而带来的相关性较差问题。

经拟合发现，在软黏土地层、粉土-粉砂性地层以及砂卵石-风化岩地层中，隧道最大隆起量Smax与lHe/H呈现出良好的线性关系，如图10所示。隧道最大隆起量预测模型为

式中：lHe/H＞0。

在软黏土地层中，拟合得到基坑开挖引起的下卧隧道最大隆起量预测公式为

在粉土-粉砂性地层中，拟合得到基坑开挖引起的下卧隧道最大隆起量预测公式为

在砂卵石-风化岩地层中，拟合得到基坑开挖引起的下卧隧道最大隆起量预测公式为

由式(4)～(6)可见，软黏土地层中拟合曲线的斜率和截距最大，粉土-粉砂性地层的次之，砂卵石-风化岩地层的最小，这说明相同条件下软黏土地层中基坑竖向开挖卸荷引起的下卧隧道隆起量最大，粉土-粉砂性地层中的次之，砂卵石-风化岩地层中的最小，这与第2节隧道竖向位移影响因素分析中得到的结论一致。

4 案例应用

4.1 工程概况

工程位于江苏省常州市，为一河道基坑开挖及跨河桥梁建设工程。河道呈东西走向，与南北走向的常州地铁1号线新桥站—新龙站区间隧道垂直交叉穿越。如何减小河道基坑开挖对下卧地铁隧道的影响是该工程重点关注的问题。

图11 所示为河道、跨河桥梁与下卧隧道位置关系示意图。河道开挖宽度为25 m，两侧设人行步道，最大开挖深度为6.6 m，河床底距地铁隧道拱顶最小距离仅4.1 m。跨河桥梁宽度为50 m，长度为36 m，上部桥面采用预制装配式简支空心板结构，桥面连续，中跨和两边跨长度分别为16 m和10 m；下部墩台采用桩柱式，墩柱直径为1.5 m，桩基采用直径为1.8 m的钻孔灌注桩。隧道为典型的城市地铁盾构隧道，隧道外径为6.2 m、内径为5.5 m、环宽为1.2 m，左、右线中心间距为14 m。

岩土工程勘察结果揭示，土层从上到下依次为杂填土(①1层)、黏土(③1层)、粉质黏土(③2层)、粉砂夹粉质黏土(⑤1-1层)、粉砂(⑤1-2层)、粉砂(⑤2层)、粉质黏土(⑦1层)、黏质粉土夹粉质黏土(⑧1层)。根据室内土体基本物理性能测试、固结试验、直剪试验等，测得各土层主要物理力学参数，见表2。河道基坑开挖主要在黏土(③1层)和粉质黏土(③2层)层中进行。

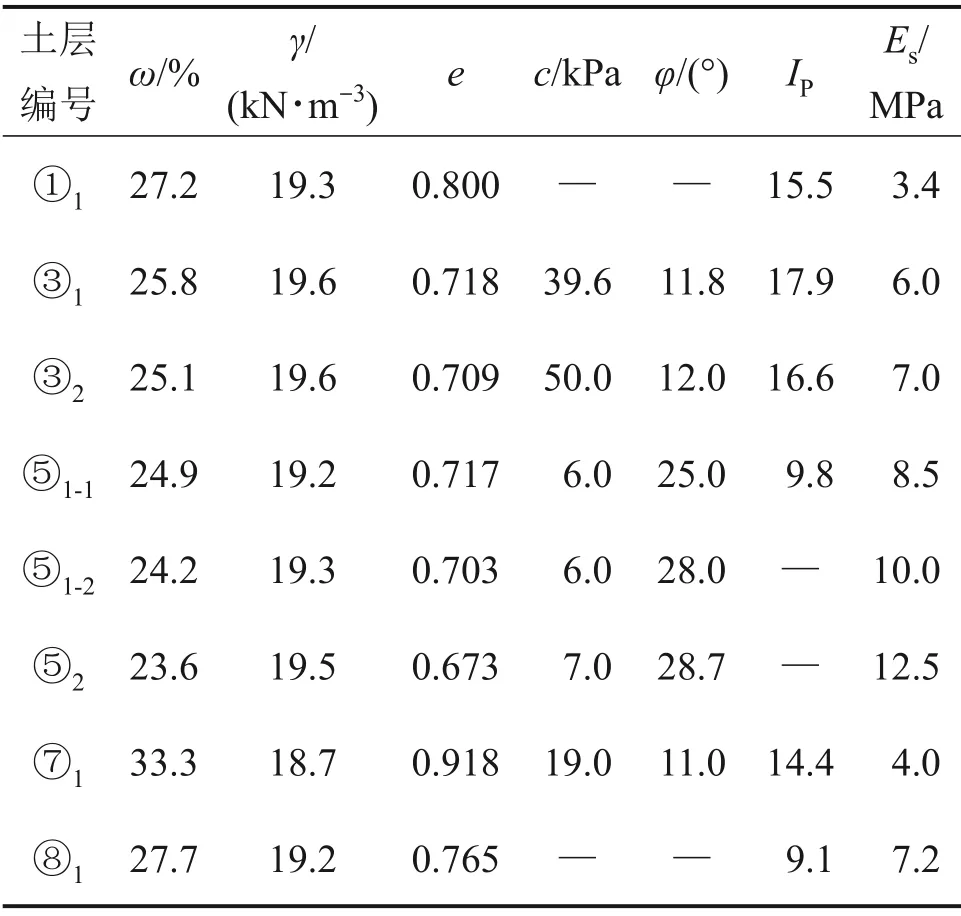
表2 土层主要物理力学参数Table 2 Physical and mechanical parameters of soil

4.2 下卧隧道隆起量预测

本文基坑开挖范围内地层主要为黏土和粉质黏土层，因此本文采用软黏土地层条件下的式(4)对下卧隧道隆起量进行预测。

河道基坑开挖深度He=6.6 m，隧道穿越基坑实际长度l=25 m，由H=He+Ht可得隧道拱顶初始覆土厚度H=10.7 m。根据式(4)，计算得出基坑开挖可能引起的下卧隧道最大隆起量为9.9 mm。

4.3 下卧隧道隆起变形现场监测

为了分析受基坑开挖影响的隧道变形响应，验证所提出的预测公式的有效性，从开挖前期到开挖结束(2018-12-06—2019-07-05)，对隧道结构进行持续跟踪监测，各监测断面及断面内监测点的位置情况详见文献[17]，监测项目包括隧道竖向位移、水平位移、径向收敛以及管片裂缝等。但由基坑开挖对下卧隧道的影响机理和多案例统计分析结果可知，下卧隧道竖向位移远大于水平位移，因此仅选择隧道竖向位移进行分析。

图12 所示为河床正下方右线隧道监测断面(Y29～Y40)和左线隧道监测断面(Z29～Z40)内测得的拱顶竖向位移随时间变化曲线。图12 中，负值表示沉降，正值表示隆起。由图12 可见，基坑开挖前地基加固、抗拔桩、桥台桩等施工造成隧道有一定程度的下沉，随后坑内土方开挖，隧道迅速隆起。若把土方开挖前的隧道状态视为变形为0的初始状态，则开挖引起的右线和左线隧道最大隆起量分别为7.5 mm 和7.1 mm。右线和左线隧道实测结果与公式预测结果较接近，差值分别为2.5 mm 和2.8 mm。由此可见，基于多案例统计得到的隧道隆起量预测公式取得了良好的预测效果。

5 结论

1)地层条件对基坑开挖引起的下卧隧道隆起量有显著影响。不同地层中，隧道最大隆起量(Smax)的平均值按从大到小顺序排列依次为软黏土地层、粉土-粉砂地层和砂卵石-风化岩地层。

2)基坑形式对开挖引起的下卧隧道隆起量有较大影响。地下室(或广场)基坑开挖引起的下卧隧道最大隆起量(Smax)比明挖通道基坑开挖引起的Smax更大。

3)基坑开挖深度(He)、开挖面积(A)、开挖卸载率(He/H)以及隧道穿越基坑长度(l)均是影响下卧隧道最大隆起量(Smax)的重要因素；随着这些参数增大，Smax有呈增大的趋势，但Smax与单个因素之间未见明显相关性。因此，科学预测开挖引起的隧道最大隆起量必须综合考虑多种影响因素。

4)考虑地层条件、基坑开挖卸载率(He/H)、隧道穿越基坑长度(l)的影响，采用lHe/H作为隧道隆起量预测指标，发现3 类地层中Smax与lHe/H均呈良好的线性关系，据此推导出了隧道隆起量预测公式。

5)工程应用结果表明，采用本文所提隧道隆起量预测公式所得结果与现场实测结果较吻合，预测效果较好。