基于LIBS谱线拟合优化的生铁硅质量分数在线检测方法

黄倩，蒋朝辉,2，谢永芳，桂卫华,2

(1. 中南大学自动化学院，湖南长沙，410083；2. 鹏城实验室，广东深圳，518000)

钢铁是制造业的关键原材料之一，高炉炼铁是钢铁生产的关键工序[1]。高炉生铁硅质量分数是衡量高炉冶炼过程中炉况稳定性与产品质量的重要生产指标，也是表征高炉热状态及其变化趋势的关键变量[2]。硅质量分数的准确检测可为高炉布料、送风等操作制度提供实时反馈信息，进而降低冶炼焦比、提升生铁质量[3]。因此，生铁硅质量分数的高精度在线检测对提升钢铁质量、降低高炉冶炼能耗具有重要意义。

目前，在高炉冶炼现场，人们主要通过对铁水采样、制样后，再使用重铬酸钾溶液滴定测量生铁硅质量分数，但该检测方法具有严重的时滞性[4]。激光诱导击穿光谱(LIBS)技术通过将脉冲激光聚焦到检测对象上，使检测对象在烧蚀过程中产生等离子体，等离子体在膨胀消失过程中自发光，使用光谱仪采集并解析等离子体的光谱信号，再根据光谱信号特征对样品进行定性与定量分析。LIBS 技术具有不受检测对象状态限制、无损快速检测等优势[5]，已成为在线成分检测的主流技术，在工业冶金、物料分类、水质土壤重金属检测等领域具有广阔应用前景[6-8]。

LIBS 技术应用于高炉生铁的相关研究较少，处于起步阶段。比利时冶金研究中心[9]使用LIBS连续测定高炉流道中铁水组分质量分数和温度；日本某钢铁公司[10]利用LIBS 实现了高炉铁水中多元素质量分数连续在线检测，但受工业现场粉尘多、辐射强等恶劣环境影响，其检测精度还有待进一步提升。针对高炉生铁硅质量分数的检测，DILECCE 等[11]通过设计延迟时间与筛选特征谱线等处理方法检测生铁硅质量分数；MEI 等[12]使用LIBS 对生铁中硅、锰、钛等元素进行偏析定量检测。以上研究使用的定标模型都是以铁为参考的内标法模型，然而单一特征谱线容易受基体效应、自吸收效应及谱线干扰的影响，对于如生铁、钢铁等体系复杂的多组分检测对象，定量分析的误差较大。为克服内标法的不足，国内外学者提出了利用多个变量建立定标曲线的多元定标法，包括多元线性回归、偏最小二乘回归、主成分分析和人工神经网络等[13-16]，在一定程度上削弱了基体效应与自吸收效应对微量元素检测精度的影响。研究表明，对于微量元素的定量分析，多元定标法能得到更精确的结果。

多元定标分析方法是提高LIBS 技术检测精度的有效途径之一。然而，目前LIBS 分析技术大都以特征谱线峰值强度替代积分强度作为输入进行定量分析，即默认所测得谱线的线型为单一线型。例如，HE等[17]使用单一Lorentz线型拟合法对钢铁中碳质量分数进行检测；FAROOQ 等[18]使用单一Gauss线型处理谱线，用于水和食品容器中聚苯乙烯和聚碳酸酯定量分析，JABBAR 等[19]使用单一Voigt 拟合谱线对盐渍土壤中栽培植物的元素进行分析。上述方法虽然可在某种程度上保障元素检测精度，但其用于生铁硅质量分数检测仍存在一定问题。一方面，在生铁硅质量分数检测中关键元素特征谱线较多，无法保证LIBS 所有谱线与理想情况下的某一种谱线加宽类型完全符合，利用单一线型拟合得到的谱线积分强度与实际谱线的积分强度存在一定偏差，导致检测结果准确率低；另一方面，谱线会因仪器性能约束而出现较短距离的偏移，中心波长、半峰宽度等拟合参数未确定，只能以实际检测值为参考依据分析[20]。理论上，LIBS 分析中要求测量出发光等离子体中对应元素全体粒子的特定跃迁的总辐射能量，即该元素在全波段的谱线积分强度[21]，但在实际处理过程中数据维数过大，检测准确率易受环境影响而波动，且检测速度也会受到影响。

为解决以上问题，本文提出基于LIBS 谱线拟合校正的方法对高炉生铁硅质量分数进行检测，具体步骤如下：1)为避免全谱段高维度分析，挑选各关键元素特征分析谱线进行积分强度提取；2)提出基于LIBS谱线展宽机制的最优线型选择方法，获取各关键元素特征谱线的最优展宽线型；3)为提升谱线拟合精度，快速求得各项拟合参数值，利用蜘蛛猴算法求解拟合线型的最优参数；4)将生铁样本原始光谱峰值强度、多种拟合方法处理后的谱线积分强度等关键特征输入到广义回归神经网络(GRNN)中，对生铁样本硅质量分数进行定量分析，以验证本文所提拟合方法的可行性。

1 基于谱线展宽机制的高炉生铁关键元素谱线最优线型选择

考虑到使用单一线型拟合的谱线与实际的谱线有一定偏差，本文基于LIBS 谱线展宽机制，提出一种高炉生铁多元素特征分析谱线最优线型选择方法。

1.1 LIBS谱线展宽机制

归一化的辐射光功率关于波长或频率的分布密度函数即为谱线线型函数。在不同频率下，光谱线型会有不同的理论分布线型，可分为Lorentz线型、Gauss 线型和Voigt 线型。对于由自然加宽和碰撞加宽所导致的均匀展宽，谱峰线型分布形式为Lorentz线型，其函数表达式IL[17]为

式中：v和v0分别为频率和中心频率；I0为谱线基底有效连续信号；A为线型拟合谱峰系数；ωL为Lorentz线型的谱线半峰宽度。

对于由热运动的发光粒子发出的多普勒频移引起的非均匀展宽，当粒子速度分布为麦克斯韦分布时，谱峰线型分布为Gauss线型，其函数表达式IG[18]为

式中：ωG为Gauss线型对应的谱线半峰宽度。

Voigt 线型是上述2 种展宽线型按一定规律得到的综合展宽线型，其函数表达式IV[19]为

式中：t为积分变量。

选取LIBS 检测1 号生铁样本光谱中硅元素与铁元素的2 段特征光谱，波长范围分别为287.7～288.6 nm和403.9～405.1 nm，分别以Si I谱线(中心波长为288.158 nm)和Fe I 谱线(中心波长为404.581 nm)为拟合中心。3种展宽线型拟合结果和残差对比如图1所示。

由图1(a)和图1(b)可知：3 种线型拟合结果在峰值强度、半峰宽度上有较大差异。从图1(c)和1(d)可看出：3 种拟合线型残差存在明显差异。在硅元素特征谱线中，Voigt线型与Lorentz线型拟合结果接近，但仍有较大差别，而在铁元素特征谱线中Voigt 线型与Gauss 线型拟合结果几乎重合，且残差相对于Lorentz 线型较小。在实际检测过程中，对同一谱峰检测数据，不同线型拟合结果所反映的峰值、积分强度等特征存在较大偏差，因此，确定特征谱峰的最优线型能够显著降低拟合误差。

1.2 谱线最优线型选择

LIBS 线型主要由波峰对应的波长、谱线轮廓覆盖的波长范围与谱线峰值一半处对应的宽度(即半峰宽度)决定。

根据定标元素特征分析谱线集中各个特征谱线波长中心，分别确定拟合的波长范围，从而避免处理全谱段高维数据。由于生铁硅元素质量分数一般小于1%，通常采用多元定标法检测；同时，还需要对生铁中其他关键元素的谱线进行特征提取。一般高炉生铁中元素质量分数如表1 所示。由表1可见：除铁元素质量分数极高外，碳元素的质量分数相对硅元素来说也较高，且变化幅度较大；锰元素与硅元素质量分数处于同一数量级，但锰元素质量分数变化幅度比硅元素的小。从美国标准与技术研究院(NIST)原子光谱数据库查找生铁中关键元素的特征谱线，从而确定关键元素特征谱线最优线型选择时的波长拟合范围。为削弱自吸收效应带来的影响，挑选铁元素的特征谱线时需避开共振线，本文选取Fe II谱线(中心波长为271.441 nm)，Fe I谱线(中心波长为346.586 nm)和Fe I 谱线(中心波长为404.581 nm)这3 条特征分析谱线。对于硅、碳、锰这3种元素，选取的分析线最好为共振线且尽量避免重叠谱线干扰的波段，以提高检出能力。本文硅元素选取Si I 谱线(中心波长为288.158 nm)，碳元素选取C I 谱线(中心波长为493.203 nm)，锰元素选取Mn I谱线(中心波长为403.076 nm)。

表1 一般高炉生铁中元素质量分数Table 1 Element mass fractions of pig iron in general blast furnace %

对生铁关键元素共挑选了6条特征谱线，假设特征谱线中第j(j= 1, 2, ···, 6)条特征光谱示意图如图2所示，其自适应地选取谱线最优线型的具体步骤如下。

步骤1：设该特征谱线中心波长为λ0，则选择与λ0最近的2 个波谷点组成的区域[vlm,vrn]即图2所示[vl7,vr7]区域，记区域内包含x个离散数据点，由图2可知x= 14。

步骤2：将区域内x个离散点用于3 种线型拟合函数。Lorentz 线型、Gauss 线型和Voigt 线型谱线的函数表达式分别如式(1)～(3)所示。

步骤4：计算x个数据点分别在3 种线型(基底信号同为波长中心位置都取拟合下的残差平方和δk(vi)。

式中：k= L, G, V，分别表示Lorentz线型、Gauss线型和Voigt线型；gk(vi)为在频率vi处，第k种线型函数下的拟合强度；Ivi为在频率vi处的检测强度。

步骤5：比较3种线型拟合结果的残差平方和，若Voigt 线型的残差平方和不是最小的，则直接选择另外2种线型中残差平方和最小的类型作为该谱线对应的理论线型；若Voigt 线型的残差平方和是最小的，判断其与另外2种线型残差平方和的相对误差绝对值是否大于5%，若是，则直接将Voigt线型作为最优线型，否则，选择与Voigt 线型拟合结果相近的Lorentz 线型或者Gauss 线型作为该特征谱线的拟合线型，以此简化运算，提高运行速度。

步骤6：对各元素特征谱线重复步骤1～5，直至所有特征谱线都得到相应的理论线型。

2 基于蜘蛛猴优化算法的高炉生铁关键元素谱线最优拟合参数获取

通过上述基于谱线展宽理论与实际数据试验得到不同频域下特征谱线的最优线型，但因仪器性能差异等造成谱线出现较短距离的偏移，峰值波长、半峰宽度等拟合参数未确定，在此条件下得到的拟合模型尚未达到最优。故得到各关键元素特征谱线对应的最优线型后，还需进一步确定对应的最优拟合参数，以提升谱线特征信息的可信度，进而提高生铁硅质量分数检测精度。

2.1 蜘蛛猴算法

本文目标函数为多目标寻优问题，故采取的寻优算法要求能同时对多个参数寻优，且要求寻优准确度高，运行速度快。蜘蛛猴优化(spidermonkey optimization,SMO)是具有竞争力的元启发式优化算法，原理简单、高效、控制参数少，在处理单峰、多峰等优化问题中具有良好的性能[22]。

SMO 算法主要思想为蜘蛛猴群体通过裂变与融合结构觅食求生。为减少成员之间的觅食竞争，蜘蛛猴群分成多个小组，母猴作为全局领导者管理所有小组。每一只蜘蛛猴代表一组可行解，每一只蜘蛛猴的位置通过全局领导者、局部领导者及小组成员位置变动进行更新，若未觅食成功则进一步细分小组，直至分裂到最大组数后进行融合，再重复分组直到觅食成功。SMO 算法很好地平衡了探索和开发能力，该算法通过前期的全局搜索和后期的局部搜索，可避免过早收敛或陷入局部最优状态，适用于待确定参数寻优，故采用蜘蛛猴算法进行优化计算。

2.2 蜘蛛猴算法获取拟合最优参数

通过LIBS 线型展宽机制得到所有特征谱线对应的最优线型，n条特征谱线组成的谱图可表示为

式中：a，b和c分别对应特征谱线中Gauss 线型、Lorentz线型与Voigt线型的谱线数量；IG(i)，IL(i)和IV(i)分别表示第i(i= 0, 1, ···,a)条Gauss函数模型拟合、第j(j= 0, 1, ···,b)条Lorentz 函数模型拟合和第z(z= 0, 1, ···,c)条Voigt 函数模型拟合的谱线光谱强度。

对应的3种线型函数拟合模型优化目标为拟合谱线与原始谱线残差σ的最小值，目标函数可表示为

式中：Ii，Ij和Iz分别表示为第i，j和z条谱线的原始谱光谱强度。由式(1)～(3)可知，Gauss 拟合模型和Lorentz拟合模型由基底信号I0、谱峰系数A、半峰宽度ωG(ωL)和中心频率v0这4 个参数确定，而Voigt 拟合模型的半峰宽度由这2 种模型的半峰宽度共同决定，即由I0，A，ωL，ωG和v0这5个参数确定。目标函数参数约束条件为

由于光谱基底信号和峰高不能为负值，优化后的谱线半峰宽度ω′L(ω′G)与优化后的中心频率v′0相比于最优线型拟合所得结果差别不会太大。

SMO 算法性能由4 个控制参数决定，包括局部领导者限制、全局领导者限制、最大组数和扰动率。结合本文目标函数特性，SMO 具体实现过程如下。

步骤1：初始化种群数量为N，可行解维度为D，最大分组数M=N/10，局部最优可行解限制次数L=D·N， 全局最优可行解限制次数G∈[N/2, 2N]，扰动率R∈[0.1, 0.8]，设单个可行解初始位置为

式中：Sij为第i(i= 1, 2, ···,N)组可行解的第j(j= 1, 2, ···,D)维；Smaxj和Sminj分别为第j维可行解搜索空间的上限和下限；U(0, 1)为[0, 1]的随机数。

步骤2：计算每个个体的适应度fi。

式中：σi为目标函数。

步骤3：对所有小组进行贪婪选择，更新局部最优可行解和全局最优可行解的位置。利用式(10)产生新的位置Snewij：

式中：为第k个群体中局部最优可行解的第j维分量；Srj为在第k个群体中随机选取的第r组可行解的第j维分量，r≠i。U(-1, 1)表示[-1, 1]的随机数。然后，比较更新前后位置的适应度，选择适应度大的位置，再根据式(11)计算各组成员被选择为最优可行解的概率：

式中：fmax为小组内个体最大适应度。通过式(12)更新选中的可行解组的位置：

式中：为全局最优可行解中随机选取的第j维分量。

步骤4：局部与全局最优可行解判定。若超过L次未更新局部最优可行解的位置，则通过扰动率R随机初始化来更新该组所有个体的位置，如式(13)所示。

若超过G次未更新全局最优可行解的位置且此时分组数量未达到最大组数M，则将种群分为更小的组；否则将所有的组融合为1个组，直到满足限制条件，得到全局与局部最优可行解。

3 实验与结果分析

3.1 实验装置与样品分析

本次研究采用的LIBS 实验装置示意图如图3所示。

激光通过聚焦透镜聚焦在样品表面，样品产生的等离子体信号由另一个透镜采集，并由光谱仪检测。其中，实验所采用的激光器为镭宝光电Dawa-200 系列Nd:YAG 激光器，最大激光输出能量约为100 mJ，脉冲频率为1～20 Hz。设置激光输出能量约为95 mJ，脉冲宽度为7 ns，脉冲频率为5 Hz，延迟时间为0.1 μs，积分时间为2 ms。从激光器发射的水平激光通过45°反射镜反射后，经焦距为50 mm的透镜垂直射到样品表面，沿45°方向侧向收集等离子体的辐射信号。辐射信号通过光纤传输到Avantes 四通道光谱仪，检测波长范围为

200～550 nm。

实验所用样品来源于某钢铁厂2 号高炉撇渣后的铁水。采取不同炉次的30 个生铁块，冷却后的生铁样品中的硅质量分数如表2 所示。对30 个生铁样品进行LIBS检测实验，按1～30号排序，其中1 号、3 号、6 号、8 号、10 号、12 号、15 号、16号、19号、20号、21号、24号、26号、28号和30号样本作为测试集，其他样本作为训练集。每个样品随机选择5个不同位置进行测量，每个位置进行220 次激光击打，其中前20 个激光脉冲用于清洁，后200个脉冲中的等离子体辐射光信号通过光纤采集，并将其传送至光谱仪进行分光。采集到被测样品的LIBS 光谱数据后，对原始光谱数据进行谱图筛选、光谱寻峰及归一化处理。

表2 生铁样品中硅质量分数Table 2 Silicon mass fraction in pig iron samples %

3.2 基于GRNN模型的定量分析

GRNN 是径向基神经网络的一种，具有优良的多变量映射能力和灵活的网络结构，在处理未知参数和非线性问题时具有较大优势[23]。同时，GRNN 优越的逼近能力和学习速度使其在分析小样本数据中十分高效。本文生铁样本数量不多，可采用GRNN模型进行分析。

根据第2节所获取的拟合最优参数得到生铁关键元素所有特征谱线的最优拟合线型，并提取特征谱线峰值强度I、积分强度S等关键特征作为模型的输入。

为避免实验条件不同带来的整体信号强度偏差，在求得所有特征谱线峰值强度与积分强度后，以基体元素Fe的相应值为基准进行归一化处理。

利用GRNN 建立生铁硅质量分数与多元素光谱谱线关键特征之间的映射关系，以峰值强度比xi1、积分强度比xi2作为网络输入，生铁硅质量分数为网络输出。

GRNN基本结构如图4所示，由输入层、模式层、求和层与输出层构成。

将提取的光谱特征参数直接作为输入层变量(x1，x2，…，xi)，即输入层的神经元个数为特征输入个数，并直接将输入变量传递到模式层，模式层的神经元数目为样本数n，GRNN的数学模型为

式中：Pi为每个模式层神经元的输出，i=1, 2,…,n；δ为扩展值；SD和SN为求和层神经元的2个输出量，其中SD是对模式层的节点输出进行算术求和，即训练样本硅元素质量分数结果，SN是对每个模式层节点加权求和；yi为第i个训练样本的硅元素质量分数离线化验值；y^i为测试样本最终得到的硅质量分数。

根据生铁中元素质量分数分布情况和生铁LIBS谱线数据初步分析结果，选取Fe II谱线(中心波长为271.441 nm)、Fe I谱线(中心波长为346.586 nm)、Fe I谱线(中心波长为404.581 nm)、Si I谱线(中心波长为288.158 nm)、C I谱线(中心波长为493.203 nm)、Mn I 谱线(中心波长为403.076 nm)这6 条特征谱线，分别编号为L1～L6，将硅、碳、锰元素分析谱线的积分强度分别除以每1条基体铁元素谱线的积分强度，得到谱线积分强度比：x1=SL4/SL1，x2=

SL4/SL2，x3=SL4/SL3，x4=SL5/SL1，x5=SL5/SL2，x6=SL5/SL3，x7=SL6/SL1，x8=SL6/SL2，x9=SL6/SL3。通过最大信息系数法对上述9个参数与硅质量分数的相关性进行分析，结果如表3所示。

表3 不同参数相关系数对比Table 3 Comparison of correlation coefficient of different parameters

最终选择谱线积分强度比x1，x2，x5，x6，x7，x8，x9这7个参数作为网络的输入；模式层神经元个数与训练样本数相等，为15 个；求和层个数为2；输出层即为硅元素质量分数，神经元个数为1。

GRNN 以非参数核回归为基础，以样本数据作为后验概率验证条件进行非参数估计，最后根据训练样本计算输入变量(谱线特征值)和输出变量(样本硅质量分数)之间的关联密度函数值，从而计算得到硅质量分数相对于输入特征的回归值。本文设置网络中核函数的扩展值δ= 1。

3.3 生铁硅质量分数定量分析结果

3.3.1 谱线拟合结果

以1号生铁样本为例，通过本文基于谱线展宽机制的最优线型选择，得到其关键元素分析谱线的最优线型结果如表4所示。表4中，-δG，-δL和-δV分别为每一条分析谱线在Gauss线型、Lorentz线型和Voigt 线型拟合下的平均残差平方和，具体选择方法参见本文第1.2节。

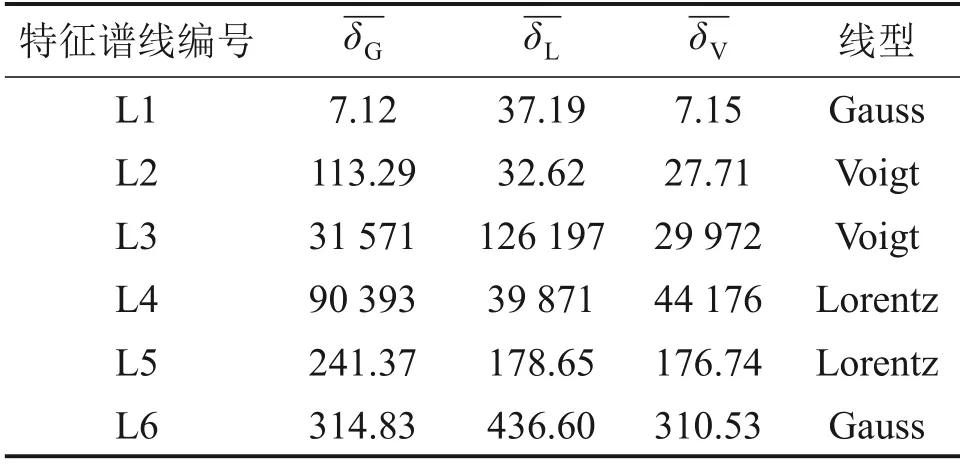
表4 1号生铁样本特征谱线最优线型选择Table 4 Optimal linear selection of characteristic spectral line of pig iron sample 1

由表4 可知，特征谱线L1 和L6 的最优线型为Gauss线型；特征谱线L2和L3的最优线型为Voigt线型；L4 和L5 特征谱线的最优线型为Lorentz线型。

下面基于蜘蛛猴优化算法得到最优拟合参数。算法初始化种群数量N设为90，初始化可行解维度D=5，则最大分组数M=9，局部最优可行解限制次数L=45，根据数据试验确定全局最优可行解限制次数G=100，扰动率R=0.6，1 号生铁样本关键元素分析谱线优化所得结果如表5所示。

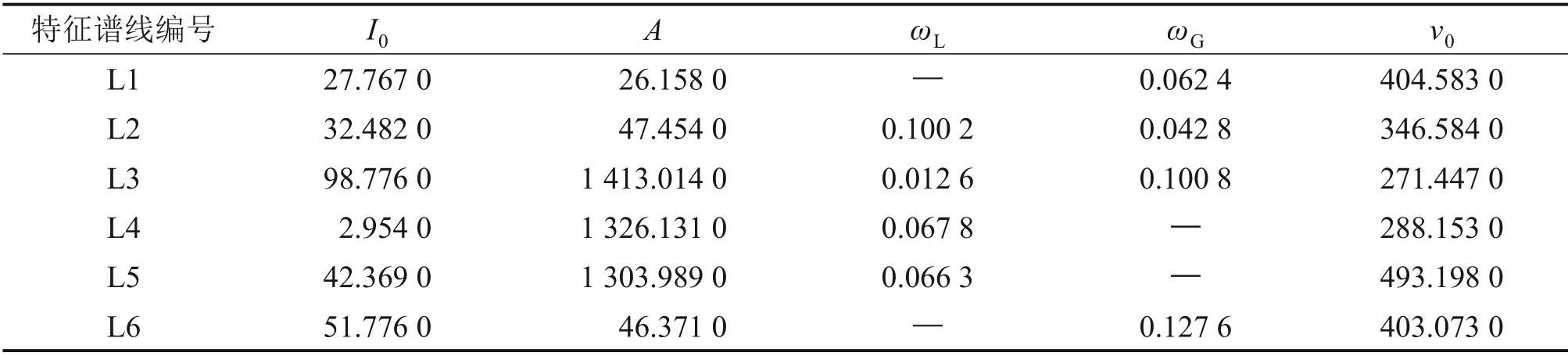
表5 1号生铁样本特征谱线最优拟合参数Table 5 Optimal fitting parameters of characteristic spectral line of pig iron sample 1

1号生铁样本所有关键元素分析线的拟合结果如图5所示。由图5可看出：每条分析线通过参数优化后，均表现出相对良好的拟合效果。

3.3.2 生铁硅质量分数定量分析结果

对生铁测试样本进行硅质量分数定量分析，并将本文拟合谱线多元积分强度内标法所得结果与传统方法所得结果进行比较，结果如图6 所示。不同方法检测精度(以确定系数R2和均方根误差eRMSE表征)对比如表6所示。

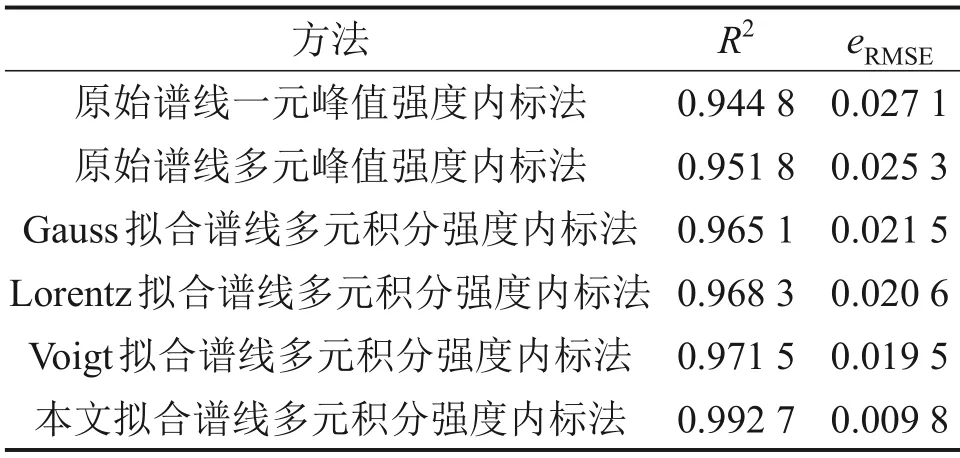
表6 不同方法检测精度对比Table 6 Comparison of detection precision of different methods

图6(a)所示为原始谱线一元峰值强度内标法的定量分析结果，其确定系数为0.944 8，均方根误差为0.027 1。图6(b)所示为采用原始谱线多元峰值强度内标法对生铁硅质量分数进行定量分析的结果，其确定系数为0.951 8，均方根误差下降为0.025 3，可见多元峰值强度内标法对微量元素的检测精度显著高于一元峰值强度内标法的检测精度。图6(c)所示为单一Gauss 线型拟合下采用多元积分强度内标法对生铁硅质量分数进行定量分析的结果，其确定系数为0.965 1，高于多元峰值强度内标法的确定系数，均方根误差为0.021 5。图6(d)所示为单一Voigt 模型拟合下采用多元积分强度内标法对生铁硅质量分数进行定量分析的结果，其确定系数和均方根误差分别为0.968 3 和0.020 6，分析效果略优于单一Gauss线型拟合下的内标分析效果。图 6(e)所示为单一Lorentz 线型拟合下采用多元积分强度内标法对硅质量分数进行定量分析的结果，其确定系数为0.971 5，均方根误差为0.019 5。

在使用同一拟合函数的情况下，使用峰值强度内标法替代积分强度内标法，可有效避免拟合谱线轮廓差异带来的影响，但这样的单点数据处理会导致谱线斜率、形状等有效信息的缺失，从而降低检测精度，而利用单一线型拟合得到的谱线积分强度与实际测得的谱线积分强度相比有一定的偏差，使得硅质量分数的检测精度降低。

本文所提LIBS 谱线拟合校正方法通过谱线展宽理论和蜘蛛猴优化算法获取到所有生铁关键元素分析谱线相应的最优线型与最优拟合参数，相较于峰值强度内标法，检测精度有大幅提升，且在一定程度上校正了谱线轮廓偏差，对生铁硅质量分数进行多元积分强度内标定量分析的结果优于使用单一线型拟合方法的结果。从表6可知，在使用本文拟合校正方法后，通过多元积分强度内标法对硅质量分数进行定量分析，其确定系数R2可达到0.992 7，均方根误差下降到0.009 8，定量分析的检测精度显著高于其他传统方法的检测精度，从而验证了本文方法的有效性。

4 结论

1)本文提出了一种基于谱线展宽机制的高炉生铁关键元素分析谱线最优线型选择方法，能够分别得到生铁关键元素分析谱线的最优线型。

2)本文提出了一种基于蜘蛛猴优化算法的高炉生铁关键元素分析谱线最优拟合参数获取方法，能够在已获取各谱线最优线型的情况下求解最优的拟合参数，减少实验环境波动、设备固有误差等因素的干扰，提升谱线拟合效果，从而提高生铁硅质量分数检测精度。

3)与一元、多元峰值强度内标法，单一Gauss线型、Voigt线型、Lorentz线型拟合后的多元积分强度内标法等传统方法相比，本文所提方法的确定系数R2较高，均方根误差eRMSE较低。