基于HITRAN光谱数据库的合并谱线测温仿真研究
贾宇杰,张丕状,戚俊成,白建胜
(中北大学 信息与通信工程学院,山西 太原 030051)
0 引 言
可调谐二极管激光吸收光谱技术(Tunable Diode Laser Absorption Spectroscopy, TDLAS)具有高灵敏度,实时响应,非接触等特点[1,2],是近年来发展较快的一种技术. 这种技术是利用气体分子对不同波长光束在不同条件下的吸收作用来确定待测参数,目前该技术已经可以做到多种气体参数的测量[3,4],其中,温度是一个关键参数,浓度与压力的反演公式均需要以得到温度为前提. 目前,TDLAS技术分为直接吸收法和波长调制法两种,直接吸收方法采集到的信号较为直观且计算简单,通过提高谱线扫描的频率加之适当的数据处理方法,也可以短时间内达到较高的检测灵敏度,满足工业现场的应用需求[5].
TDLAS技术在测温时一般基于双线测温法,选择相对独立的谱线,或者使用拟合程序对叠加的谱线进行分离. 以水分子谱线为例,Rieker[6]使用7 203.9 cm-1和7 435.6 cm-1两条谱线在吸收池和激波管测量了气体温度,为一条独立谱线和叠加谱线,测量温度最高达1 050 K; Zhou[7]在1.8 μm附近对10对谱线进行了筛选,最终选定5 553.8 cm-1和5 554.2 cm-1在单激光传感器中使用,为两条独立谱线,并进行了实验验证; 李金义[8]选择6 807.86 cm-1和7 185.59 cm-1作为吸收谱线,为一条独立谱线和叠加谱线,测量Hencken型平面火焰燃烧炉的温度. 低浓度的条件下谱线展宽较窄,容易筛选出相对独立的谱线,但在被测气体浓度比较高时,谱线宽度的增加会导致谱线间相互叠加出现干扰[9],难以分辨出原有的谱线形状,从而使温度计算出现误差. 因此,如何处理高浓度情况下的干扰谱线,具有一定的研究意义和应用价值. 合并谱线测温法基于双线测温法,不同是将相互叠加的一组谱线视为测量谱线进行温度计算,恰好契合高浓度条件下的谱线叠加情况.
本文选择对水分子合并谱线测温方法进行研究,寻求高浓度条件下干扰谱线纳入温度计算中的可行性. 从HITRAN数据库获取谱线参数和配分函数,在此基础上模拟谱线强度与温度的关系,并在原有双线测温法基础上得出合并谱线测温方程,以6 808 cm-1和7 194 cm-1附近水分子谱线为研究对象,给出应用时选择谱线的依据和拟合过程,并通过仿真证明作为研究对象的两条谱线利用合并谱线方法测温的可行性.
1 基本原理
由Beer-Lambert定律可知,吸收度α(ν)有以下关系[10]

(1)
式中:ν为激光波数,cm-1;L为穿过被测场光程,cm;P为场内气体压强,atm;X为吸收组分摩尔浓度;S代表吸收谱线强度,cm-2·atm-1;T为待测场温度,K;φ(ν)为吸收谱线线型函数;α为吸收系数.

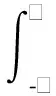
(2)
式中:S(T)表示为仅与温度有关的函数,但谱线事实上有不同的温度特性,其数学表达[10]为

(3)
式中:S(T0)是参考温度T0下的吸收谱线强度;h为普朗克常量;c为光速;k为玻尔兹曼常数;E″(cm-1)为吸收谱线对应的跃迁前低能级能量;ν0为吸收谱线中心频率;Q(T)为气体分子的配分函数.
双线测温法需要两条合适的谱线作为测量对象,当两条谱线在同一环境下时,光程、 浓度、 压强均相同,因此,它们的积分吸收度之比根据式(2) 可简化为线强之比

(4)
式(4)经过一定程度的变形,可以得到直接吸收法的测温相对灵敏度公式

(5)
式(1),式(2)为单条谱线的吸收度和积分吸收度的计算方式,如果需要计算数条谱线叠加情况下的积分吸收度,根据式(2),可以表达为

表 1 不同温度下主要谱线的谱线强度(单位: cm/molecule)Tab.1 The intensity of the main spectral lines at different temperatures (cm/molecule)

表 2 主要谱线的低跃迁态能量Tab.2 Lower-state energy of main spectral lines
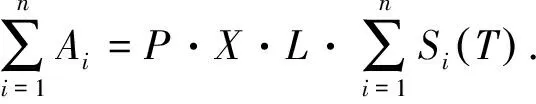
(6)
可以看到,数条谱线的积分吸收度与多个因素有关,因此,需要双线测温法剔除其他环境因素的影响,假设另一个积分吸收度也是由多条谱线叠加获得,参考式(4),两个积分吸收度比值

(7)
式(7)即为合并谱线测温方程,在谱线确定的情况下,影响积分吸收度比R的值只有温度T,但由于该方程为超越方程,无法得到T的解析解,因此,只能通过多项式拟合得到T关于R的关系式T(R),在实际测量时得到R后代入T(R)中即可求得温度.
2 仿真与分析
2.1 谱线选择依据
首先对谱线仿真和谱线参数进行分析,阐明选择6 808 cm-1和7 194 cm-1两组水分子谱线的依据.
图1 为水分子不同浓度下7 194 cm-1附近的谱线仿真与6 808 cm-1附近的谱线仿真,设定光程1 cm,压强为1 atm,温度为1 500 K,浓度为10%~40%,各谱线的参数取自HITRAN数据库中的对应谱线,在此基础上依照beer-lambert定律计算出谱线线型. 可以看到两组谱线的周边没有其他较强的谱线,有一定的独立性.
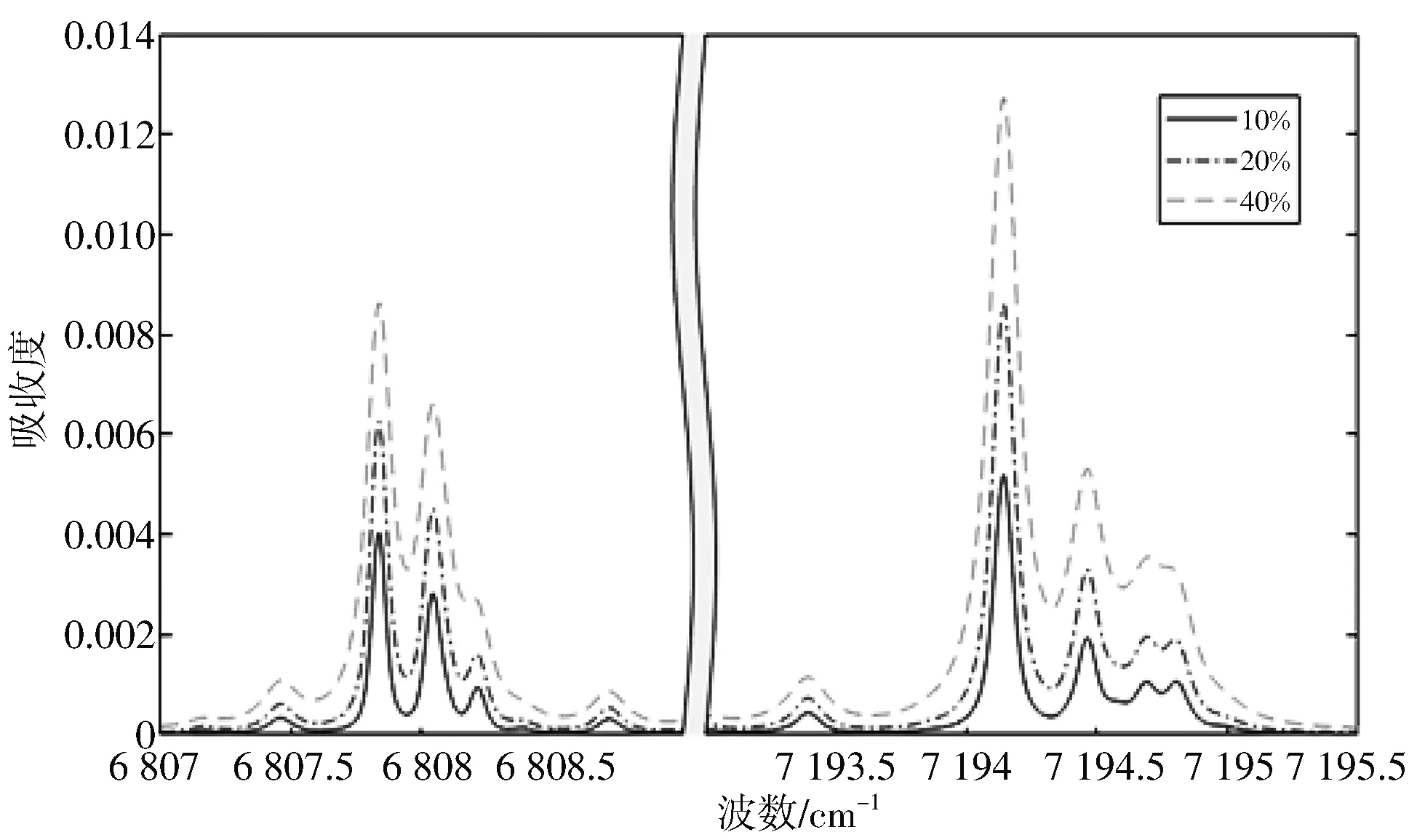
图1 水分子在6 808 cm-1附近和7 194 cm-1附近的吸收线型仿真Fig.1 Linear simulation of absorption of water moleculesnear 6 808 cm-1 and 7 194 cm-1
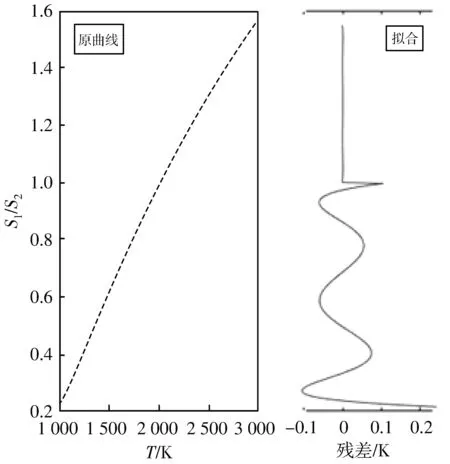
表 1 为图1 中出现的主要谱线在不同温度下的强度,综合表 1 和图1 可以看出,从1 000 K开始,除谱线7 194.14 cm-1仍与其他谱线差距较大外,各谱线的强度较为接近. Zhou为保证吸收谱线的信噪比接近,推荐的线强比范围0.2 式(5)在不同温度下的意义为: 一对谱线的测温灵敏度由环境温度和低跃迁态能量差决定,环境温度越高,测温灵敏度越低,反之,低跃迁态能量差越高,测温灵敏度越高. 因此,一般在利用此方法进行高温测量时,需要能量差较大的谱线,一般情况下要求灵敏度大于等于1[8,11],以保证温度变化时积分吸收度之比有足够的响应. 经计算,在测量1 000 K以上温度时,能量差需要满足低跃迁态能量差大于1 390 cm-1. 从表 2 数据显示,7 194 cm-1附近与6 808 cm-1附近的任意两条主要谱线的低跃迁态能量差最小,为1 391.8 cm-1,符合上述条件. 综合以上3点,判断两组谱线适用于本文测温方法. 接下来以6 808 cm-1和7 194 cm-1两组谱线为研究对象,将参数代入公式进行仿真,评价其测温性能. 由表 1 可知7 194.14 cm-1与6 807.83 cm-1分别为两个谱线组中最强的谱线,按式(5)和式(7) 表示,谱线组的积分吸收度之比等价于谱线强度和之比,则两个谱线组强度最大的两条谱线对各自的积分吸收度之比的影响最大. 图2 的①~④分别为不同温度下7 194 cm-1和 6 808 cm-1谱线组的谱线强度之和,以及两个谱线组的最强谱线 7 194.14 cm-1与 6 807.83 cm-1的谱线强度的仿真结果,可以看到,①③和②④在谱线强度与温度关系上,谱线组的谱线强度与谱线中的单条谱线趋势相同,且强度有所增加,分别增强1.25倍和2.81倍,可以避免单条谱线强度过低而导致不适用于测量. 图2 不同温度下谱线组强度和与谱线强度Fig.2 The sum of the two spectral line groups intensity and thespectral line intensity in different temperatures 图3 表示了图2 中曲线①③的比值和曲线②④的比值,根据式(7),比值等价于积分吸收度之比,图中两个谱线组的积分吸收度之比的斜率高于两个单独谱线的积分吸收度之比的斜率,意味着比值法测温的条件下,相比于利用单独谱线,合并谱线的积分吸收度的比值对温度更为“敏感”,相同的温度变化下比值的变化幅度更大,不同温度下比值的斜率提升可达20%~60%,这意味着更好的抗干扰能力. 图3 不同温度下两条谱线组强度和之比及两条谱线强度之比Fig.3 The ratio of the sum-intensities near the two spectral linesand the ratio of the spectral line intensities at different temperatures 图4 为参考式(5)计算的合并谱线测温相对灵敏度与传统的双谱线测温相对灵敏度的对比,传统双谱线测温依然使用7 194.14 cm-1和6 807.83 cm-1两条谱线,可以发现,在相同两组谱线内,基于合并谱线的双谱线测温比传统的双谱线测温具有更强的灵敏度,1 000 K~3 000 K范围内,合并谱线法平均高0.88,图4 中3 000 K时的合并谱线灵敏度为 2.009,说明300 K~3 000 K范围内基于合并谱线的双谱线测温灵敏度均大于2,这个值高于李金义等给出的灵敏度大于1的推荐范围[8,11]. 图4 不同温度下合并谱线测温与双谱线测温相对灵敏度Fig.4 Relative sensitivity of combined spectrum temperature measurementand double spectrum temperature measurement at different temperatures 由于在实际测量时,式(7)无法解出反演公式,必须通过拟合得到比值和温度的近似关系. 图5 左侧的原曲线是截取图3 中两谱线组积分吸收度之比R>0.2部分所得,另一曲线是以Y轴为基准,以R等于1为分界点的分段5阶多项式拟合结果. 这样做有两个好处: 一是可以直接得到关于比值的温度函数; 二是分段拟合可以有效减少残差. 拟合结果如图5 右侧所示,R>1时拟合结果较好,残差小于1/‰,0.2 图5 1 000 K~3 000 K积分吸收度比值拟合结果Fig.5 1 000 K~3 000 K integral absorbance ratio fitting results 本文基于HITRAN数据库,以6 808 cm-1附近和7 194 cm-1附近两组水分子谱线为对象,进行基于双线测温法的合并谱线测温方法研究. 首先是对两组谱线中几条主要谱线的一些测温指标进行量化分析,从谱线组的相对独立性,主要谱线的线强比范围和最小低跃迁态能量差出发进行分析,得到了两组谱线适合利用合并谱线方法进行温度测量的结论. 利用传统双线测温公式,推导出了合并谱线测温方程和该方法下相对灵敏度表达式,从合并谱线测温方法的角度对一些指标进行了仿真,并与两组谱线中最有代表性的两条谱线7 194.14 cm-1与6 807.83 cm-1的指标进行对比,发现两组谱线在1 000 K~3 000 K均有更好的测温性能. 合并谱线测温方法针对上述两组谱线进行测温时有以下几点改善: ① 改善了单条谱线强度过低的问题; ② 改善了积分吸收度比值; ③ 改善了相对灵敏度. 最后对积分吸收度比值曲线进行了拟合,以多项式拟合的方式获得了较高的精度. 通过以上工作证明了6 808 cm-1和7 194 cm-1两组谱线用于基于双线测温法的合并谱线测温方法的可行性,以合并计算的方式消除了干扰谱线的影响,为高温高浓度环境下的测温研究奠定基础.2.2 公式仿真与分析



3 结 论

