深部开采岩体围压卸荷-渗流致拉破裂机制

李春元，崔春阳，雷国荣，左建平，于 祥，何 团，李向上，杜伟升

(1.煤炭科学研究总院有限公司 深部开采与冲击地压防治研究院，北京 100013；2.中国矿业大学(北京)力学与建筑工程学院，北京 100083)

经过长期大规模开发，我国浅部煤炭资源开采殆尽，资源开发逐渐向地球深部进军；尤其作为煤炭消费主力的中东部地区华北型煤田主要矿井开采深度已高达800～1 000 m，并已有50余座超千米采深矿井，最大采深已达1 501 m。而深部岩体典型的高地应力、高渗透压力等复杂地质力学环境极易造成突水灾害，尤其在深部高地应力及高承压水作用下，深部岩体结构的有效应力升高，强烈的开采扰动造成高应力岩体卸荷并驱动煤岩体裂隙变形破裂，使得岩体渗透性增加，并导致深部开采突水概率增大，突水灾害频发，从而威胁矿井安全生产及职工的生命财产安全。

根据以往突水实例，突水地点多位于采场或采空区，并表现为滞后型突水；而采场或采空区岩体均处于应力卸荷状态，由此形成了非平衡条件下采动岩体由动态渐进破裂演化至失稳灾变的非线性过程。为研究采动岩体的卸荷破坏及渗流问题，国内外专家学者开展了诸多研究并取得了较为丰硕的研究成果。如邓华锋等考虑卸荷速率和孔隙水压力因素开展了砂岩三轴卸荷试验，研究了两因素对砂岩卸荷特性的影响；刘新荣等分析了初始卸荷水平与水压条件影响下砂岩的卸荷变形破坏力学特性和本构模型；梁宁慧等试验研究了应力卸荷过程中裂隙岩体的渗透系数变化规律；刘先珊等考虑卸荷作用建立了卸荷应力与渗透系数的关系；王如宾等考虑初始围压、卸荷速率等进行了三轴卸荷渗流力学试验；于洪丹等试验研究了加卸载作用下含裂隙砂岩和粉砂岩的渗流特性。这些成果促进了卸荷岩体力学理论的快速发展，并为研究矿山采动岩体的卸荷-渗流破坏机制奠定了基础。

而深部开采活动作为“高应力(地应力)+动力扰动(开采卸压)”双重作用的力学过程，岩体破裂既取决于自身材料特性，又受内部裂隙结构控制；且由于应力卸荷，裂隙岩体的变形差异使得岩体将承受与卸荷面垂直的拉应力，或在应力卸荷作用下岩体可视为承受了与卸荷方向平行的拉应力，从而影响岩体的卸荷-渗流致裂机制。

为研究卸荷条件下裂隙岩体的变形破坏及裂隙扩展演化规律，黄达等研究得到卸荷岩体裂隙的扩展是在卸荷差异回弹变形引起的拉应力和裂隙面剪应力增大而抗剪力减小的综合作用下产生的破坏；刘磊等研究了岩质边坡卸荷裂隙在拉剪应力状态下的损伤演化本构模型，应用破坏度表征了岩体内部的破坏状况；黄厚旭等以卸荷取芯岩柱为对象，建立了饼芯厚度与初始应力的关系，研究了其拉应力导致的间隔断裂机制；吴汉辉等结合卸荷岩体的拉剪应力状态，确定了节理岩体的线性断裂力学模型，并对裂隙岩石的变形进行了评估。为进一步研究非均匀岩体的卸载拉裂机制，王明洋等推导获得了岩石在裂隙缺陷区域的局部拉应力变化规律，明确了卸载拉裂的时间效应。这些成果为研究岩体的应力卸荷状态和卸荷作用下岩体的拉破裂机制提供了新的思路和方法，但针对卸荷-渗流过程中拉应力的产生及其致拉破裂机制的研究仍较少，应力卸荷与渗流对煤岩体拉破坏的影响机制仍不清晰。

基于此，笔者结合深部开采承压水压力变化实际，应用裂隙附近的应力集中演化方程分析了深部开采岩体围压卸荷-渗流过程中拉应力的演化规律，研究了岩体围压的卸荷-渗流致拉破裂机制，获得了深部开采岩体卸荷致拉破裂与渗流的关系，从而揭示了深部开采岩体的卸荷-渗流突水机制。

1 深部开采承压水压力变化规律

承压水压力是煤层突水的基本动力，其大小决定着采动岩体突水与否及突水量的大小。而受区域地质及埋深影响，岩体内承压水水压不断变化；为了解不同采深下承压水压力的变化规律，结合华北型煤田邯郸-邢台矿区、焦作矿区、肥城矿区、淮北矿区等典型大水矿区的主要生产矿井资料，不完全统计绘制了底板岩体承压水压力与采深的关系曲线，如图1所示。

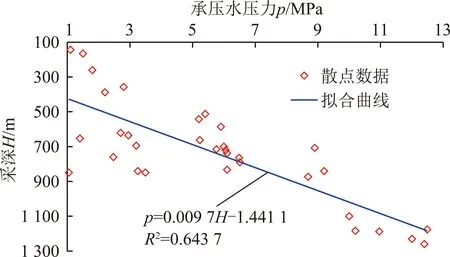
图1 华北型煤田底板承压水压力与采深关系

根据图1，华北型煤田底板岩体承压水压力随采深增加总体呈升高趋势，其散点数据的线性拟合曲线为=0.009 7-1.441 1，拟合优度为0.643 7。与地应力随采深变化规律类似，的表达式中含一个系数和常数项，系数表示承压水压力随采深变化的程度，常数项则表明受区域地层及构造影响承压水压力将产生一定的变化。为进一步反映承压水压力的物理意义，并预估同一矿井不同深度区域的承压水压力大小，可将与的拟合关系方程表示为

=+

(1)

式中，，为拟合系数，可结合区域地层及构造变化实测确定；为水的容重。

因此，随采深增加，承压水压力的增加一定程度上将增加岩体突水的危险性，尤其在岩体孔隙、裂隙发育情况下，深部开采扰动使得承压水压力与岩体内应力耦合，将进一步加剧隔水层内岩体的破裂程度，并使得岩层突水机率增加。

2 深部开采岩体围压卸荷-渗流致拉力学机制

煤层开采前，深部岩体承受准静水压力作用，其围岩垂直主应力与水平主应力相等，即=≈，其中，为覆岩容重。根据矿山压力原理及采场前后底板垂直应力与水平应力分布规律，绘制了采动底板岩体的应力分布示意，如图2所示。

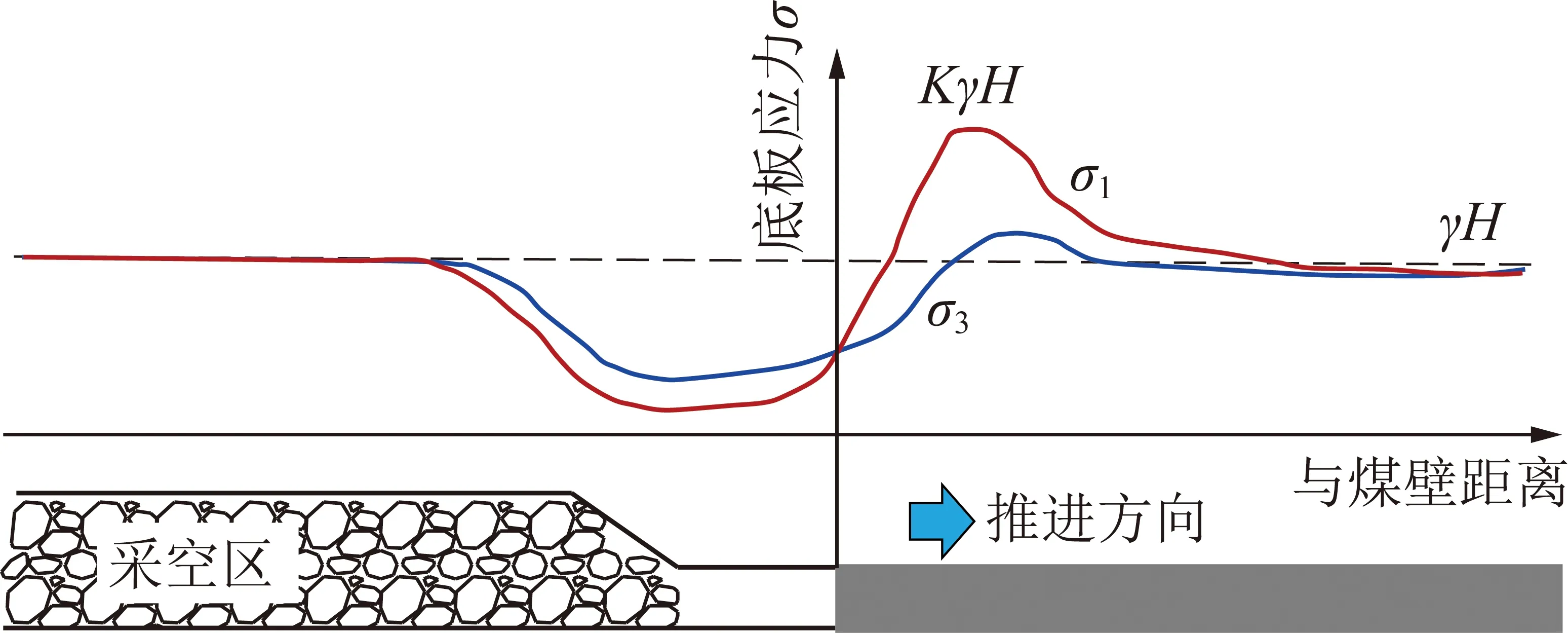
图2 采动底板岩体应力分布示意[27-31]

煤层开采后，采场超前底板岩体支承压力显著增加并向底板深部传播，导致底板岩体应力变化。在采场超前底板区域，岩体的垂直应力及水平应力由原岩应力缓慢增加至峰值，但垂直主应力峰值=高于水平应力峰值，且前者距煤壁的距离较后者近，其中为开采引起的应力集中系数，一般取2～3；在采场底板前方一定距离范围内，岩体应力由峰值开始卸荷降低，直至采场或采空区底板区域，应力卸荷至最低值。由此可知，在采场超前底板岩体围压开始卸荷，直至采空区底板区域，从而不断影响着岩体的破裂演化及致灾机制。

2.1 岩体围压卸荷-渗流致拉应力演化规律

为研究围压卸荷-渗流过程中深部岩体内拉应力的演化规律，设岩体在垂直方向轴主应力为=；水平方向,轴的主应力分别为==。为便于计算并研究围压卸荷-渗流的时间效应及围压卸荷-渗流过程中岩体内拉应力变化，暂不考虑围压卸荷至拉应力的情形，令,轴方向围压自线性卸荷至0，轴应力=并保持不变，卸荷过程中任意时刻为，卸荷总时间为，其中0<≤，则岩体的围岩应力环境可用式(2)表示，其中压应力为负值，深部岩体的应力卸荷演变状态如图3所示。

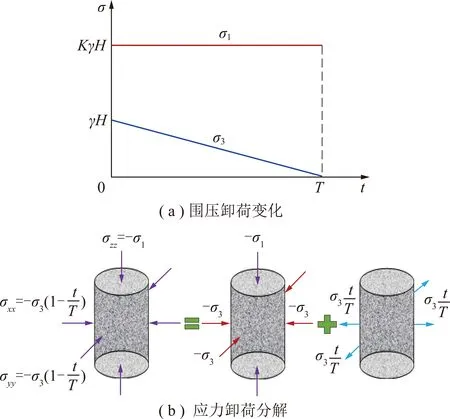
图3 深部岩体应力卸荷演变示意

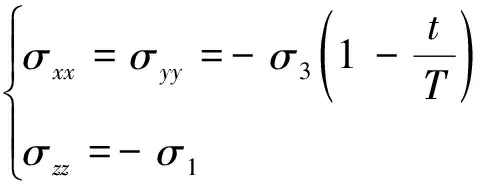
(2)

考虑岩体内孔隙、裂隙等结构的渗流影响时，在开采扰动应力与承压水压力共同作用下，裂隙岩体的应力-应变关系可通过有效应力原理得到，有

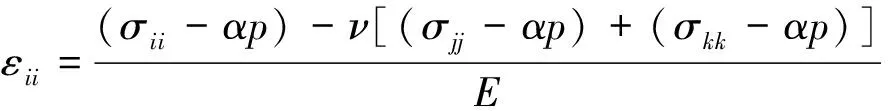
(3)

式中，,,=,,；，分别为岩石的弹性模量和泊松比；为岩体内承压水压力的作用系数。

岩体围压卸荷时，裂隙破裂前忽略裂隙内承压水压力的卸荷作用，联合式(2)，(3)可计算岩体在，，方向的应变()，()，()为

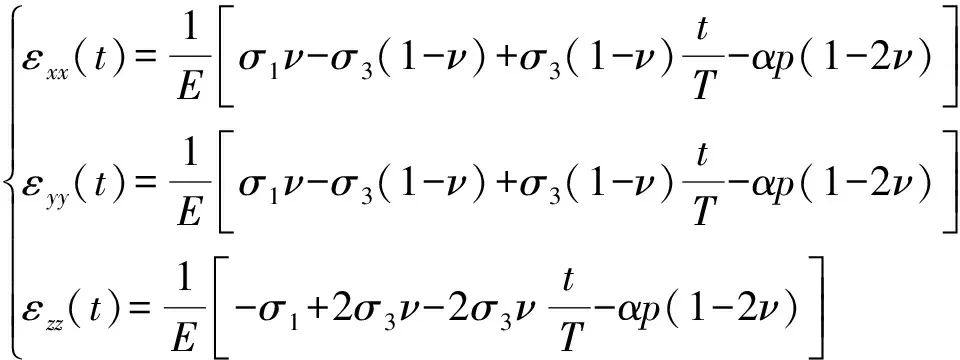
(4)

根据岩体内部构造的自相似性，岩体内裂隙的准弹性体在整体宏观角度仍为连续弹性体，但裂隙附近将出现应力集中，从而改变岩体内的应力场。设岩体内裂隙的尺寸为，若，及的作用时间足够长，岩体中裂隙处的应力集中已经完全松弛，则该裂隙处应力集中的演化方程可用式(5)表示，以此可分析应力卸荷-渗流影响下岩体内裂隙附近的应力状态。

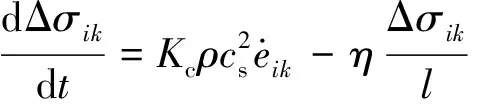
(5)

式(5)右侧第1项表示剪切应变造成的附加应力；第2项表征附加应力的松弛特性，并设dΔ/d与裂隙引起的附加应力梯度成正比。为分析岩体内裂隙处沿轴、轴方向卸荷-渗流产生的应力Δ，Δ，可将式(5)变换为

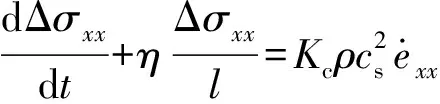
(6)

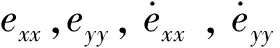
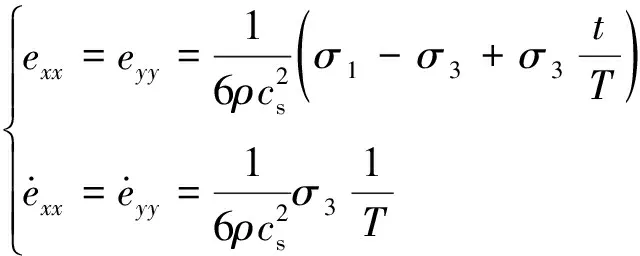
(7)

将式(7)代入式(6)，可得一阶非齐次线性微分方程，其解为

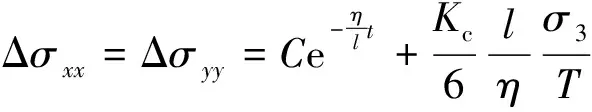
(8)

式中，为积分常数。

当=0时，岩体未卸荷，则Δ=Δ=0，代入式(8)，则可得式(8)的解为

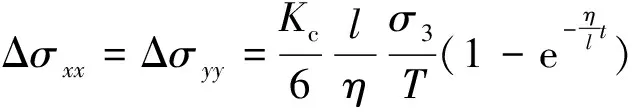
(9)

根据式(9)，Δ，Δ≥0，则深部岩体围压卸荷-渗流时，在岩体内部形成了与围压方向相反的附加应力，该附加应力为与卸荷方向平行的拉应力，并可能导致拉破裂产生，其与岩体单轴压缩及初始静水压力作用下轴向卸荷时形成的拉应力形式相似，且考虑卸荷-渗流时间及有效应力后承压水压力对该岩体围压卸荷产生的拉应力无任何影响，即承压水压力不会对围压卸荷-渗流产生附加拉应力。

但由于深部岩体裂隙破裂前，岩体内充满了具有一定压力的承压水，在压应力状态下承压水对岩体产生拉应力作用，且在岩体卸荷破裂前承压水压力大小及其对裂隙的张拉作用不随卸荷-渗流时间而改变。因此，承压水压力在岩体裂隙内与围压卸荷方向相同，并且作用于整个裂隙边缘(图4)，其将与岩体围压卸荷形成的附加拉应力叠加，则岩体裂隙将沿轴、轴方向卸荷-渗流产生拉应力ΔT，ΔT为

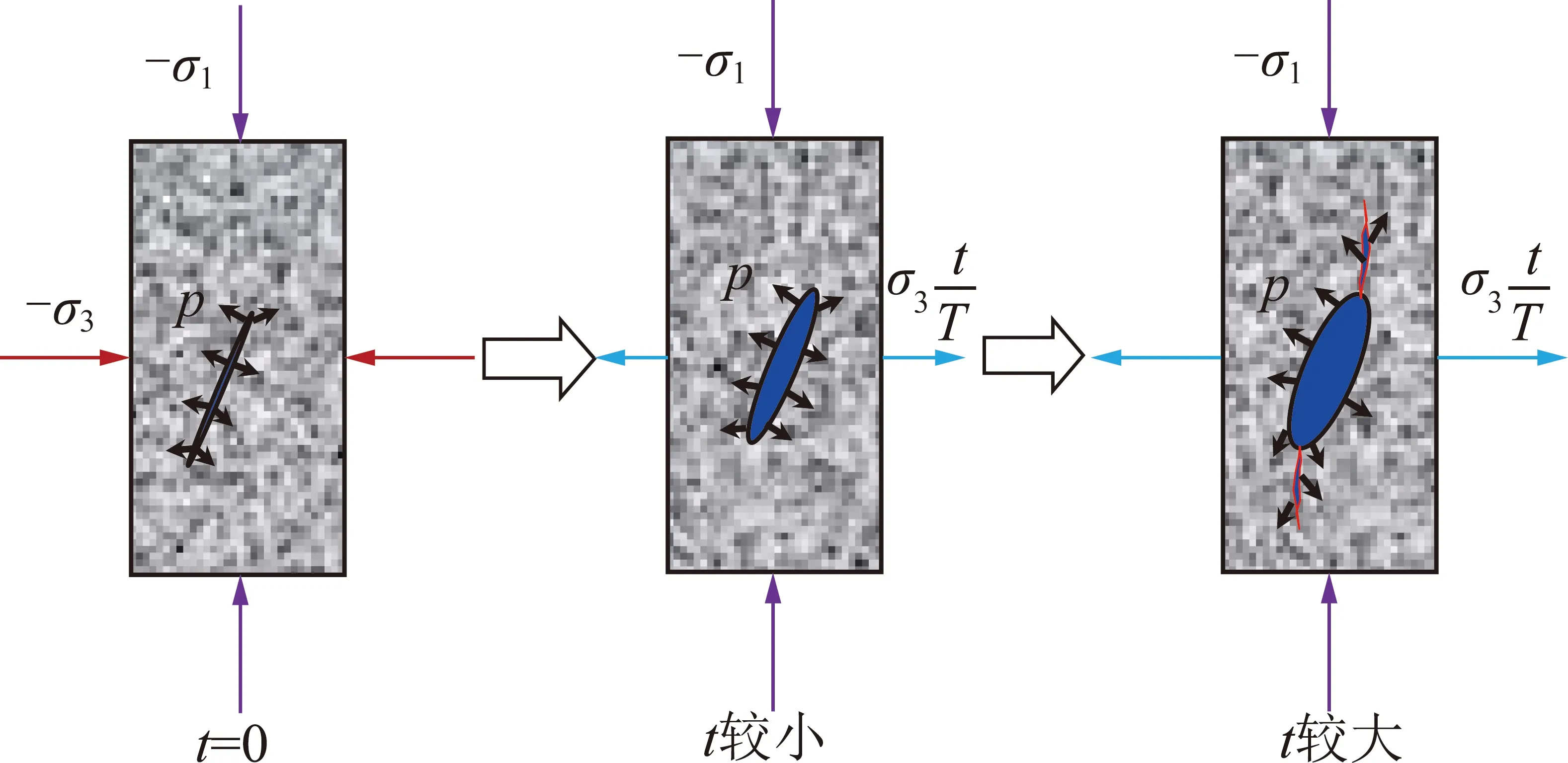
图4 岩体围压卸荷-渗流致拉影响下裂隙变化示意

ΔT=Δ+，ΔT=Δ+

(10)

联立式(9)，(10)，并将≈代入，可得

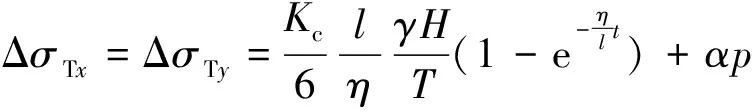
(11)

由式(11)知，由于岩体内部裂隙和承压水水压的作用，岩体围压卸荷-渗流过程中产生的拉应力与，，，，，，及等参数密切相关，并随，及增加而增大，随增加而降低，但受与的比值大小影响，其大小将产生一定变化。同时，由于该拉应力的存在，将导致深部岩体裂隙由=0时的压缩闭合状态向>0时的张开状态转变，如图4所示。随增加，ΔT，ΔT增加，裂隙开度相应增加；当增加至一定值时，岩体裂隙可能由于卸荷-渗流过程中拉应力的升高导致裂隙产生拉破裂，并造成岩体渗透率发生变化。

为进一步分析深部开采岩体围压卸荷-渗流对拉应力影响，结合河南能源集团赵固一矿二煤层工程地质及底板突水实际，取=1，=，=27 kN/m，=700 m，=2×10m/min，根据图1拟合曲线计算，=0.7；在煤系地层中，10～10m的微裂隙密布，取=2×10m；分别令=2，10，30，60，90 min代入式(11)，绘制了不同卸荷-渗流时间下岩体内拉应力变化曲线，如图5所示。

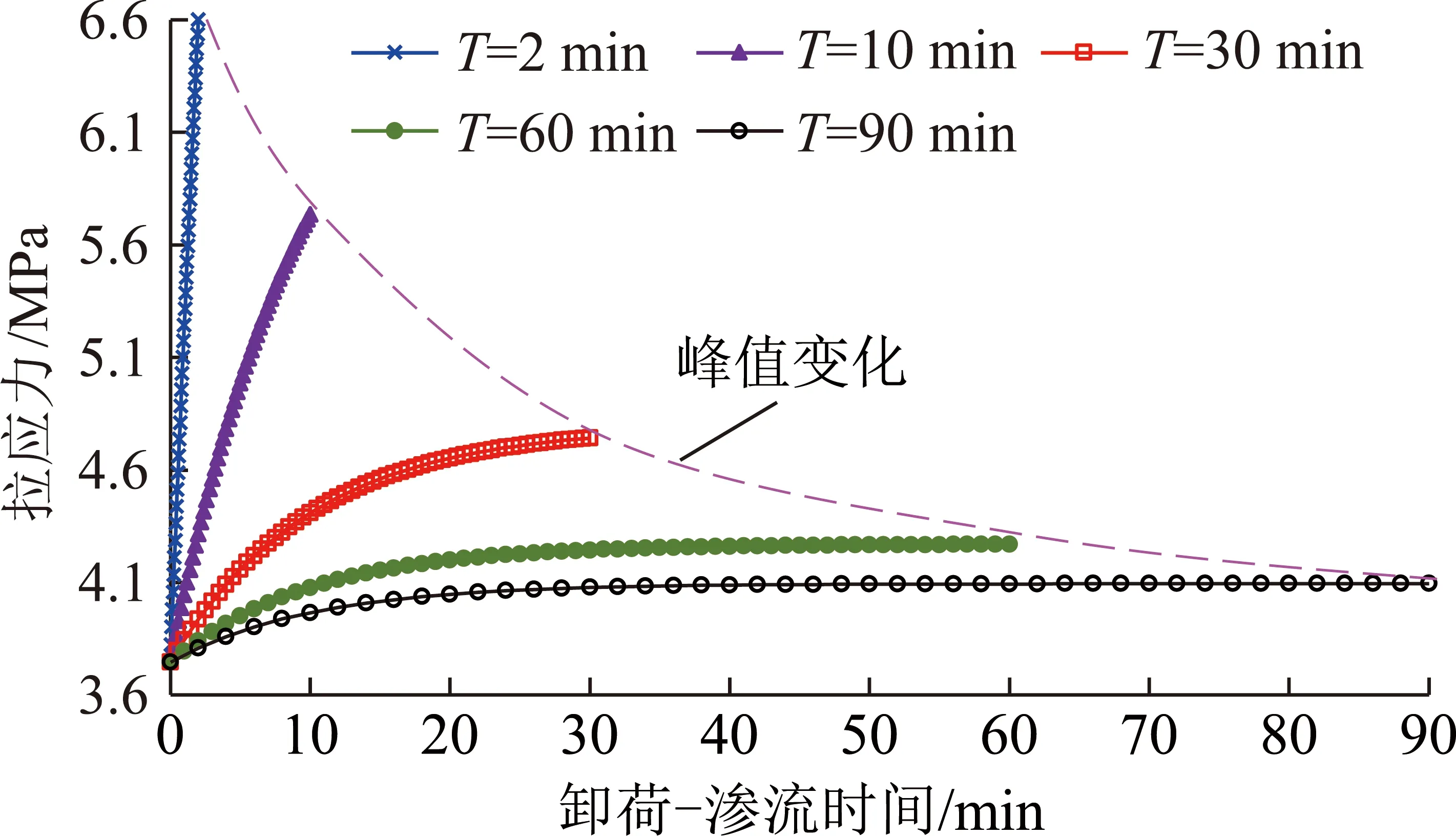
图5 不同卸荷-渗流时间下岩体内拉应力变化

根据图5，围压卸荷-渗流总时间不同，岩体内拉应力变化较大。当=2，10 min时，拉应力随卸荷-渗流时间延长近似线性增高；≥30 min，拉应力则在短时间内先快速增加后变缓而呈非线性增高规律；故越小，ΔT或ΔT增加速率越快，并越接近于线性增高。同时，越大，岩体卸荷-渗流产生的拉应力峰值越低；随增加，拉应力峰值先快速下降后缓慢减低。当=2 min，拉应力峰值为6.60 MPa；当=90 min，拉应力峰值降低至4.09 MPa，2者相差2.51 MPa，故岩体内拉应力大小与其围压的卸荷-渗流总时间密切相关。

为分析裂隙尺寸及对岩体内拉应力峰值的影响，分别变换，，并令=，其余参数不变，计算获得了裂隙尺寸及应力集中系数影响下拉应力峰值的变化曲线，如图6所示。

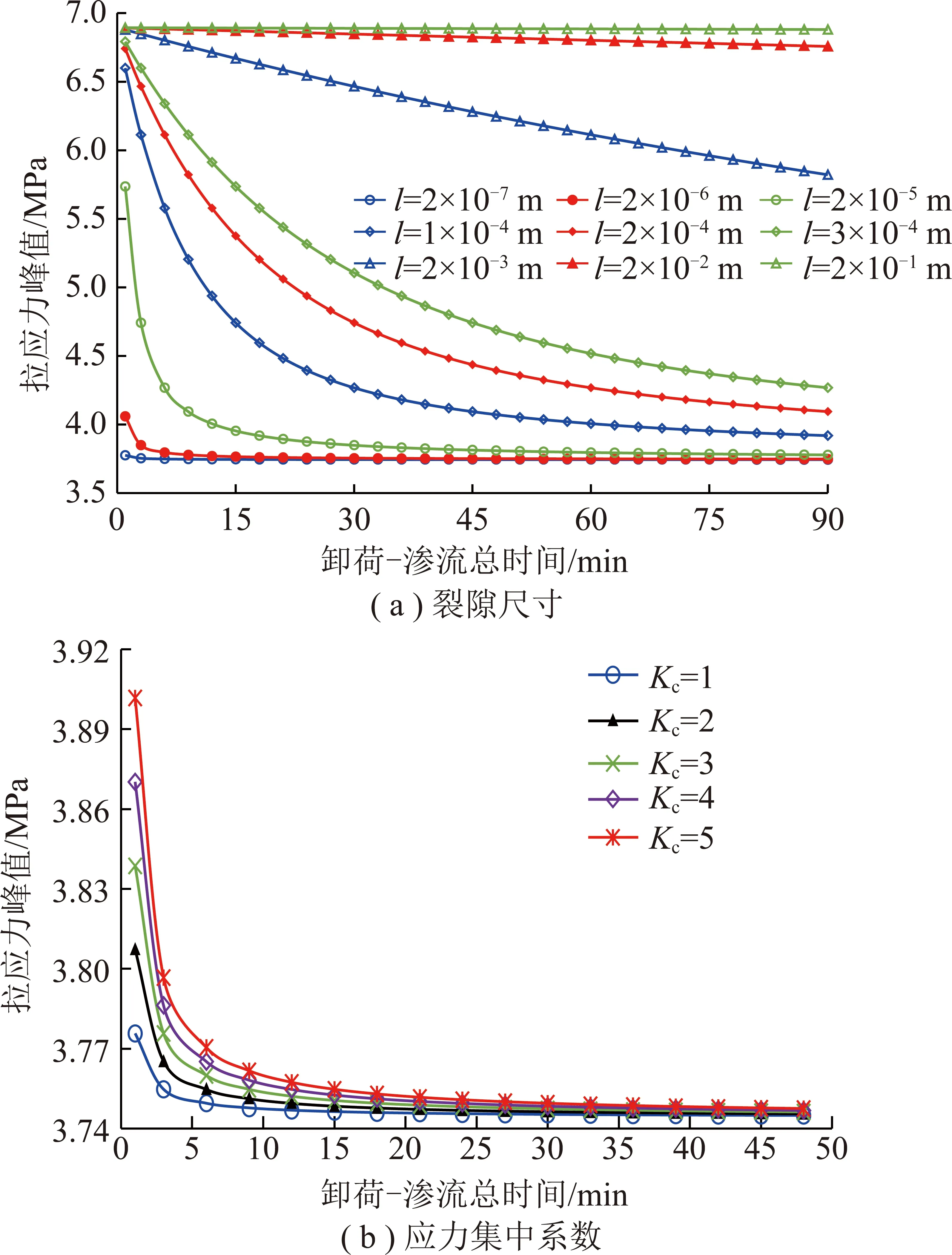
图6 裂隙尺寸及应力集中系数影响下拉应力峰值变化曲线

由图6(a)可知，越大，围压卸荷-渗流产生的拉应力峰值越高。=1 min时，若=2×10m，拉应力峰值为3.78 MPa；若=2×10，2×10m，则拉应力峰值分别为6.74，6.89 MPa，增加3个数量级，拉应力峰值分别增加2.96，0.15 MPa，故增加，拉应力峰值差异减小。当=1×10，2×10及3×10m时，仅变化0.1 mm，拉应力峰值变化曲线间距相差较大；而≤10m或>10m量级时，拉应力峰值变化曲线间距相差却很小；因此，在为10m量级时，拉应力峰值变化最为敏感。同时，当<3×10m时，拉应力峰值随非线性降低；当>2×10m时，拉应力峰值随则线性降低。

根据图6(b)，变化，围压卸荷-渗流导致的拉应力峰值虽有变化，但变化很小。=1 min时，若=1，拉应力峰值为3.78 MPa；而若=5，拉应力峰值也仅3.90 MPa；增加4，拉应力峰值仅增加0.12 MPa；故拉应力峰值变化对的敏感性低。

为进一步分析承压水压力及采深对拉应力峰值变化的影响，分别变换，，并令=，其余参数不变，计算获得了承压水压力及采深与岩体内拉应力峰值关系曲线，如图7所示，其中图7(a)中=30 min，图7(b)中固定为5.0 MPa。

图7 采深及承压水压力与岩体内拉应力峰值关系

根据图7(a)，随承压水压力增加，围压卸荷-渗流导致的拉应力峰值线性增加，且同一下，增加，拉应力峰值线性增加。由图7(b)可知，不同围压卸荷-渗流总时间影响下，采深增加，岩体内拉应力峰值均线性增加；图7(b)中=1 500 m时，围压卸荷-渗流导致的拉应力峰值差异最大，=10 min，其拉应力峰值为7.77 MPa，=50 min时则降低至4.84 MPa，2者相差2.93 MPa。

2.2 深部开采岩体卸荷-渗流致拉破裂机制

由式(11)及图5知，随岩体卸荷-渗流持续，ΔT，ΔT均随卸荷-渗流作用时间持续而非线性增长，从而在卸荷-渗流完成时刻达最大值。在ΔT，ΔT作用下，岩体内裂隙张开(图4)；当ΔT，ΔT增加至一定值后，由于裂隙开度的不断增加，将造成岩体克服其自身围压限制及裂隙结构抗拉强度而产生拉破裂，即岩体裂隙产生卸荷-渗流致拉破裂的条件为

ΔT≥-或ΔT≥-

(12)

联立式(2)，(10)及式(12)，可得

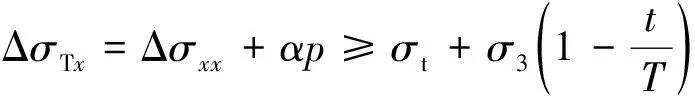
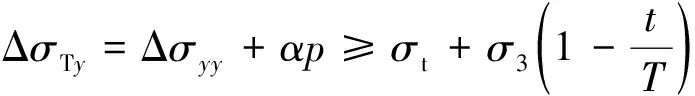
(13)

令

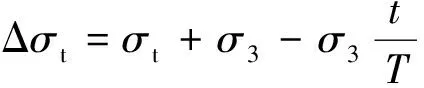
(14)

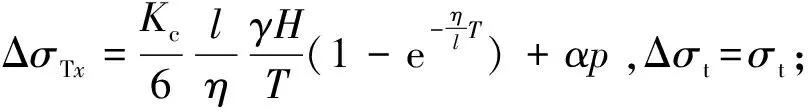
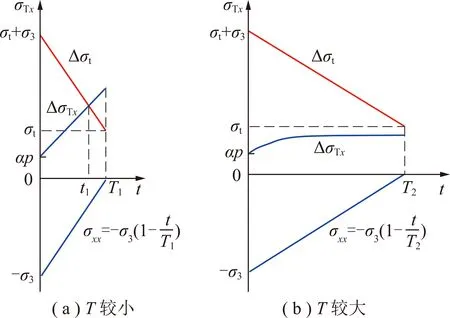
图8 深部岩体围压卸荷-渗流致拉破裂机制示意

同时，受围压卸荷-渗流总时间影响，岩体内拉应力峰值明显不同。当较小并为时，围压卸荷-渗流导致ΔT在短时内快速增加，并首先超过裂隙的抗拉强度，如图8(a)所示，但在围压限制作用下岩体内无破裂产生；随后，在时刻，曲线ΔT与Δ相交，即ΔT≥Δ=+(1-/)，岩体内拉破裂产生，并将导致岩体内裂隙扩展。而当较大并为时，卸荷-渗流产生的ΔT峰值很小，如图8(b)所示，ΔT与Δ并未相交，即围压卸荷-渗流完成后，ΔT最大值仍小于，则岩体围压卸荷-渗流产生的拉应力将不会导致拉破裂产生。

而在煤系地层岩体中，广泛分布着各种不同尺寸的裂隙及节理层理等，其中大尺寸裂隙主导着岩体的渗透性能及致灾程度。根据式(11)，若岩体卸荷-渗流过程中远远大于，则e-→0，故可将式(11)应用Maclaurin公式展开为

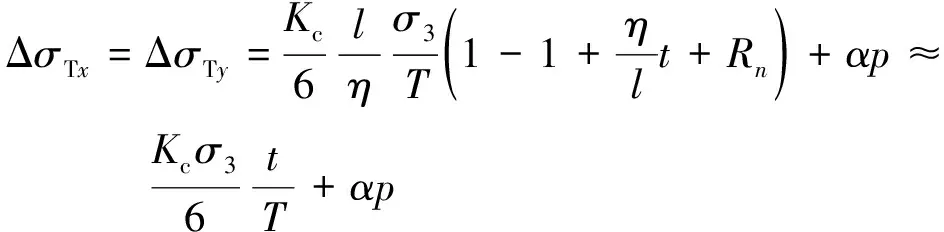
(15)

式中，为式(11)中指数函数应用Maclaurin公式展开的余项。

因此，在围压卸荷-渗流过程中，可将岩体内拉应力的演化规律简化为随时间线性变化，如图8(a)所示。同时，联立式(13)，(15)，可得

(16)

简化，可得

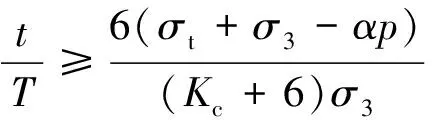
(17)

根据应力卸荷量定义可知

(18)

结合式(2)中0<≤，则0<≤100%。而考虑到现场工程及室内试验实际，围压卸荷至0后，若岩体仍未完全破坏，则围压可继续卸荷至拉应力，直至超过岩体的抗拉强度而产生破裂，故可大于100%，并表示岩体卸荷至拉应力状态。

联立式(17)，(18)，并将≈代入，可得

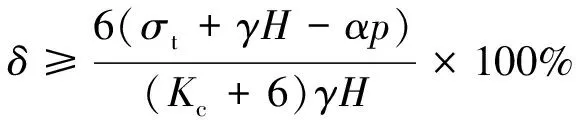
(19)

据此可知，在卸荷-渗流总时间一定情况下，当围压卸荷量达到一定阶段时，岩体围压的卸荷-渗流作用将导致拉破裂产生；故试验或现场开采时，可用岩体卸荷量估算岩体的拉破裂条件，从而获取岩体内发生拉破裂的临界值。为分析采深、承压水压力及裂隙结构抗拉强度对深部岩体围压卸荷-渗流致拉破裂的影响，分别以，，，为变量，=0.7，=27 kN/m为常量，代入式(19)计算获得了岩体围压卸荷-渗流致拉破裂的卸荷量临界值变化规律，如图9所示。图9中卸荷量临界值大于100%表示岩体围压卸荷-渗流致拉破裂时需要卸荷至拉应力状态，其忽略了岩体应力单纯受拉破坏影响；受区域地层或构造影响，根据图1拟合曲线计算可能存在一定误差，若≤148.6 m，计算时忽略承压水压力作用，即令=0，下文不再赘述。

图9 岩体围压卸荷-渗流致拉破裂的卸荷量临界值变化规律

根据图9(a)，在=3.0 MPa情况下，=1时，若=100，400，700，1 000及1 300 m，卸荷量临界值则分别为180.95%，95.97%，82.34%，76.88%及73.95%，依次降低84.98%，13.63%，5.46%，2.93%。故随采深增加，围压卸荷-渗流致拉破裂的卸荷量临界值差异逐渐减小，在700 m以浅非线性快速降低，700 m以深则近似线性降低，即采深越大，围压卸荷-渗流致拉破裂的卸荷量临界值越低，围压卸荷-渗流越易导致岩体产生拉破裂。若=700 m，分别为1，2，3，4，5时，则卸荷量临界值分别为82.34%，72.05%，64.04%，57.64%，52.40%，依次降低10.29%，8.01%，6.40%，5.24%，故随增加，卸荷量临界值同样非线性降低。但与相比，卸荷量临界值对的变化更敏感。结合式(1)，(19)知，在岩体材料自身强度不随与改变的前提下，代表了应力因素，表征了岩体材料的平均应力水平，其变化量直接与卸荷量临界值相关；而仅与岩体内部的裂隙尺寸、形状等材料属性相关，且煤系地层岩体材料属性变化不大，故对岩体卸荷-渗流致拉破裂而言，对卸荷量临界值的敏感性明显高于，这也从侧面说明了深部开采诱发的卸荷-渗流灾变现象更为剧烈。

由图9(b)知，在=3.0 MPa，=1情况下，随承压水压力增加，围压卸荷-渗流致拉破裂的卸荷量临界值均线性降低，且采深越浅，线性降低速率越快。同时，不同采深的承压水压力与卸荷量临界值关系曲线均相交于同一点，结合式(19)计算知该交点处=4.29 MPa，=85.71%；当<4.29 MPa时，越小，临界值越高；当>4.29 MPa时，越小，临界值越低；因此，采深越小，卸荷量临界值对的变化越敏感。

由图9(c)知，在=1，=5.0 MPa情况下，随裂隙结构抗拉强度增加，围压卸荷-渗流致拉破裂的卸荷量临界值均线性增加，且采深越浅，线性增加速率越快。与承压水压力的影响类似，不同采深的岩体抗拉强度与卸荷量临界值关系曲线均相交于同一点，交点处=3.5 MPa，=85.71%；当<3.5 MPa时，越小，临界值越低；当>3.5 MPa时，越小，临界值越高；故不同采深相比，采深越小，卸荷量临界值对的变化越敏感。

根据图9，围压卸荷-渗流致拉破裂的卸荷量临界值仅在采深较浅时才会高于100%，即岩体需要卸荷至拉应力状态才可导致拉破裂；而采深增大至一定深度后卸荷量临界值开始小于100%，即采深增加，岩体可不需要卸荷至拉应力状态即可导致岩体拉破裂。因此，受采深增加影响，围压及承压水压力的增加，使得岩体的卸荷-渗流能力增强，并促使岩体出现拉破裂的机率增高。

3 深部开采岩体卸荷致拉破裂与渗流关系

深部开采后，受围压卸荷-渗流影响，岩体内裂隙将首先张开，随ΔT，ΔT增加，裂隙开度不断增加，并造成渗透率增加；而拉破裂作用将使得岩体的渗透能力进一步增强。根据前述，可将围压卸荷前后轴向应力对岩体渗透率的贡献作用视为不变，基于Bandis双曲线裂隙变形公式，可获得卸荷作用下裂隙岩体的渗透率：

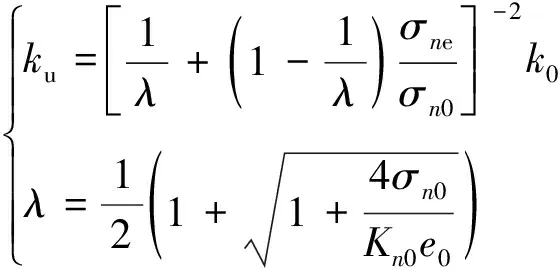
(20)

式中，为变形系数；0，e分别为围压卸荷开始时、卸荷过程中岩体的法向应力；为卸荷开始时裂隙岩体的渗透系数；为卸荷裂隙的初始开度；0为卸载裂隙的法向刚度。

同时，岩体裂隙破裂前满足有效应力原理，0，e取正值，即0=-，e=(1-/)-，将其代入式(20)，则

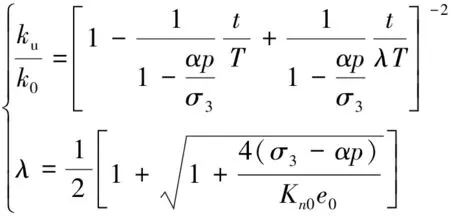
(21)

联立式(18)，(21)，并将≈代入，可得

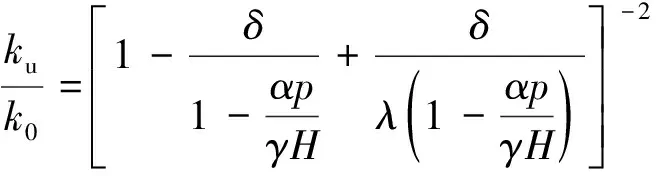
(22)

根据式(22)，受采深、承压水压力及围压卸荷量影响，深部开采后岩体围压卸荷将导致渗透率发生非线性变化；当岩体卸荷-渗流产生拉破裂后，必然导致渗透率的显著增长。为了具体分析采深、承压水压力及围压卸荷量对渗透系数的影响规律及围压卸荷致拉破裂与渗透的关系，令0=2.0 GPa，=1.0×10m为常量，分别变换，及计算获得了不同承压水压力及采深下卸荷岩体的渗透率变化曲线，如图10，11所示。

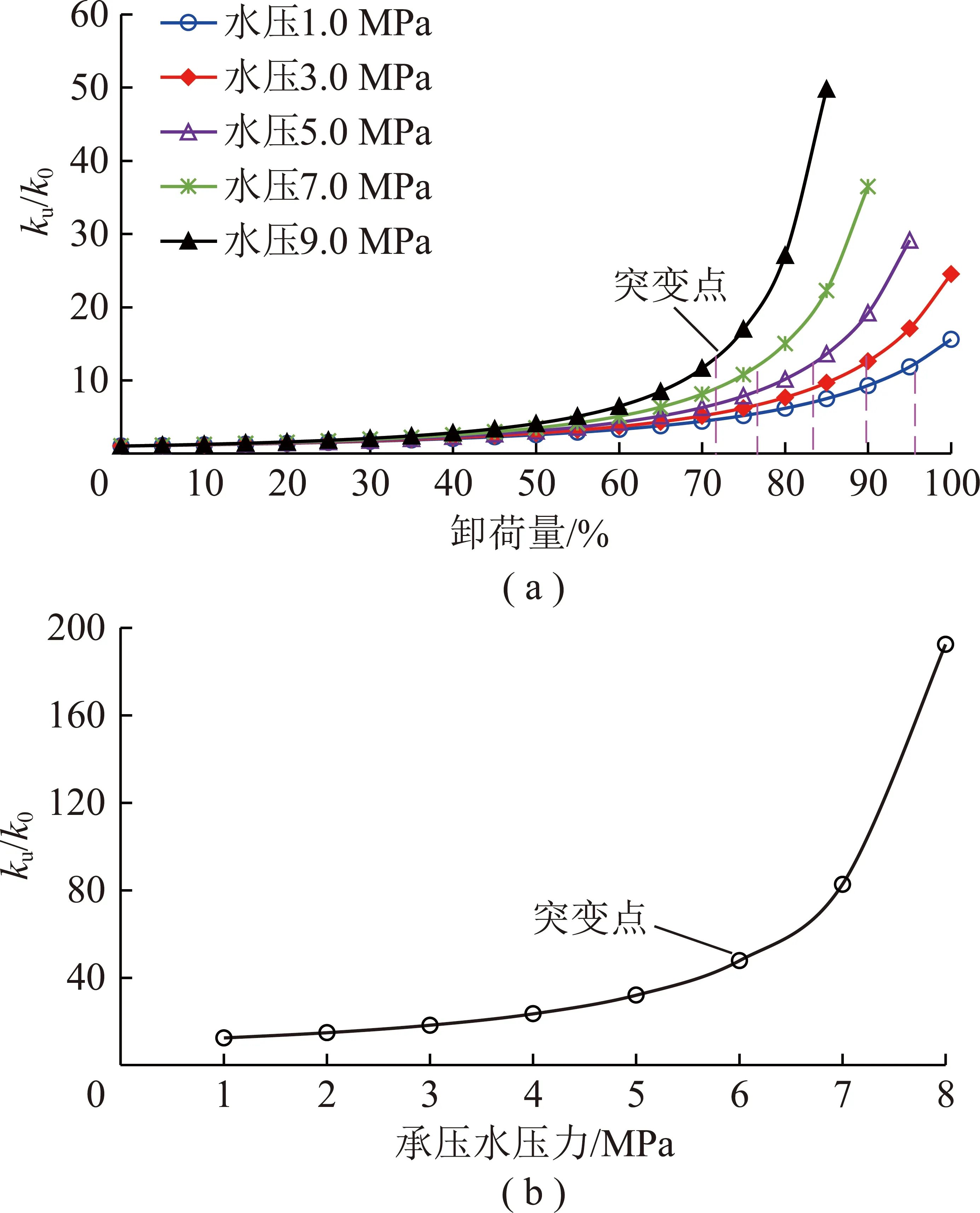
图10 不同承压水压力下卸荷岩体渗透率变化曲线

根据图10(a)，采深=700 m时，随增加，不同承压水压力下渗透率均非线性增加。≤50%时，不同下/的差异很小，均近似为线性增加；如=50%，为1.0，9.0 MPa时/分别为2.55，4.08，2者仅相差1.53。而>50%时，在作用下/快速增加，直至骤然突变；且越大，/突变增加规律越明显；如=85%时，为1.0，3.0，5.0，7.0及9.0 MPa，/则分别为7.49，9.67，13.61，22.27，49.76，依次增加2.18，3.94，8.66，27.49，差距越来越大。同时，令=3.0 MPa，=1，根据式(19)计算了=1.0，3.0，5.0，7.0及9.0 MPa时的临界值分别为96.15%，89.80%，83.45%，77.10%，70.75%，并将其用粉色虚线标注在了图10(a)中。分析发现，不同承压水压力下高于其卸荷-渗流致拉破裂临界值后/均出现了骤然突增，临界值成为/骤然增加的突变点；且越大，突变点的临界值越小。结合图10(b)，一定，随增加，/也将突变增加，故承压水压力增加至一定值将造成深部开采岩体出现卸荷-渗流致拉破裂。

根据图11(a)，同承压水压力与卸荷量的关系一致，随增加，不同采深下/均呈非线性突变增加。≤50%时，不同下/的差异很小，均近似为线性增加；如=50%，在100，1 300 m下/分别为1.63，3.86，两者仅相差2.23。而>50%时，在增加作用下/快速增加，直至骤然突增；且越大，/突变增加规律越明显；=100，400，700，1 000及1 300 m时，的临界值分别为180.95%，95.97%，82.34%，76.88%，73.95%，即越大，突变点的临界值越小。且在一定情况下，随增加，/突变增加，如图11(b)所示。故采深增加至一定值时岩体围压的卸荷-渗流也将导致岩体产生拉破裂。

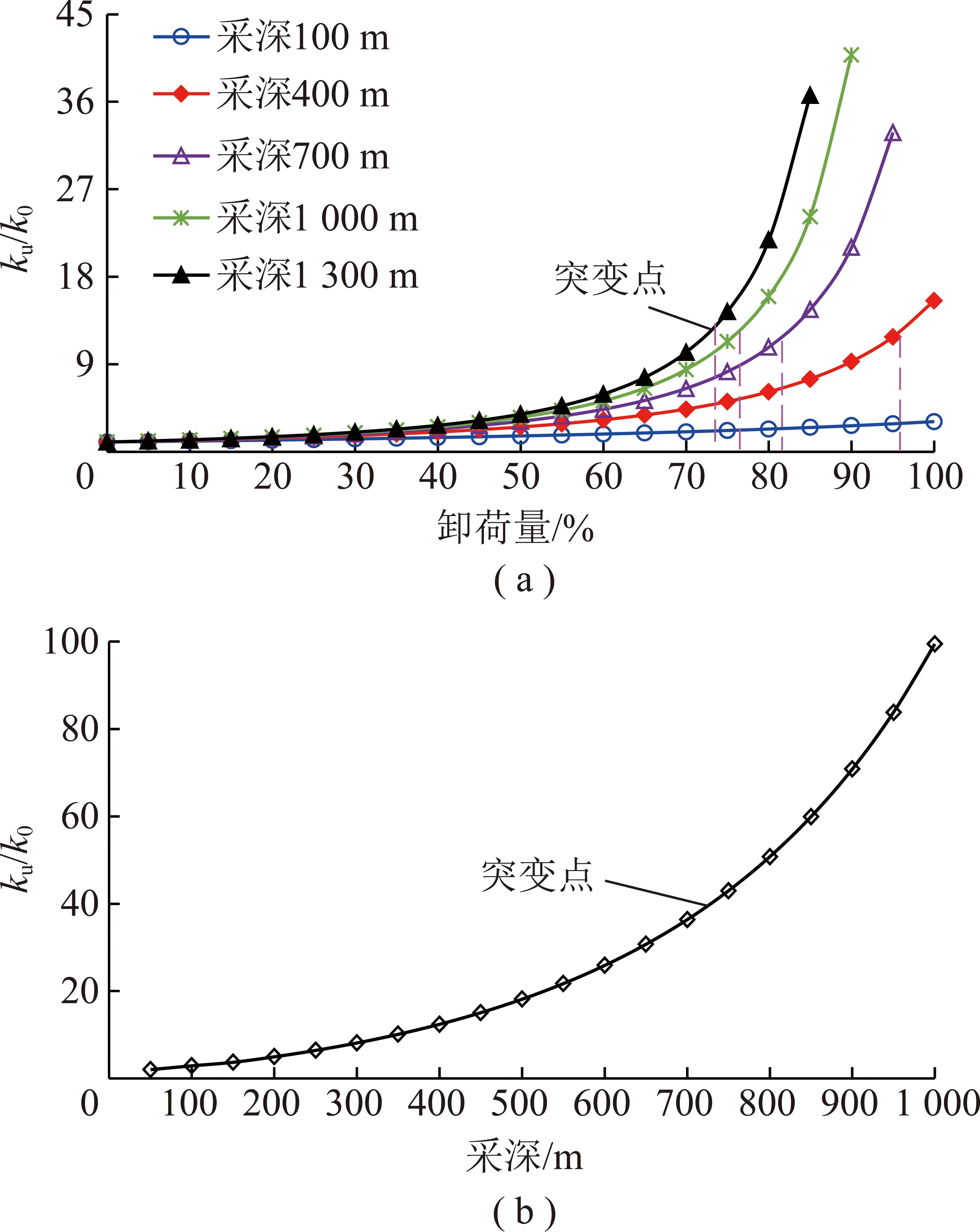
图11 不同采深下卸荷岩体渗透率变化曲线

同时，根据式(19)及图9，减小及增加，将造成裂隙岩体的临界值减小，则/突变点同步减小，从而更利于岩体的渗透率突变。因此，深部开采岩体的卸荷-渗流致拉破裂将造成岩体渗透率的突变增加；且承压水压力及采深越大，越利于岩体渗透率突变，故深部开采围压的卸荷-渗流作用极易导致隔水层岩体由渗水向突水转变。

4 深部开采岩石围压卸荷-渗流试验

为进一步验证深部开采岩体围压的卸荷致拉破裂机制及其与渗流的关系，在室内应用GCTS RTR-1000型三轴应力-渗流力学试验系统开展了不同围压下岩石试件的卸荷-渗流致裂试验，试样取自河南能源集团赵固一矿二煤层，并在室内加工为50 mm×100 mm的标准试件。

为快速获取岩石围压卸荷过程中渗透率的变化并避免液渗过程中进回液管频繁被煤屑或充填物堵塞问题，应用纯度99.999 5%的高纯惰性气体氦气采用瞬态法测渗透率，计算方法为

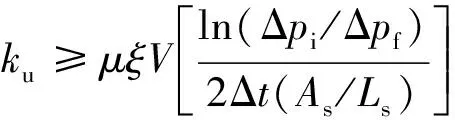
(23)

式中，，分别为高纯氦气的黏度系数和压缩系数；为高压气瓶容器体积，8 L；Δ，Δ及Δ分别为渗透率测试初始压力差、结束压力差和测试时间，岩石试件上下端面压力差保持在0.35～0.65 MPa，测试时间不低于10 min；，分别为试样高度及其截面积。

根据深部采动岩体所经历的应力环境变化及式(2)，制定了岩石试件的加卸载应力路径，试验时先对编号为TU-4，TM-2，TM-3的试件分别加围压至预定值(初始围压分别为17.5，21.5，25.5 MPa，其对应的采深分别为648，796，944 m)，再将轴压逐步加载至岩石试件接近屈服状态，停止加载，并作为围压卸荷的起始点测一次渗透率。随后，保持轴压不变，对岩石试件卸围压，围压每卸荷2 MPa测一次渗透率，直至岩石试件完全破坏，再测一次渗透率。加卸载速率采用位移控制，控制速度为0.05 mm/min。

试验完成后，根据式(23)计算了不同初始围压下岩石试件围压卸荷过程中的渗透率，获得了不同围压卸荷状态与围压卸荷起始点的渗透率比值/，并结合式(18)计算了不同卸荷状态下围压的卸荷量，绘制了不同采深下岩石围压卸荷量与渗透率比值关系图，如图12所示。

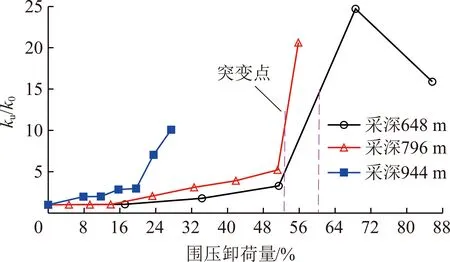
图12 不同采深下岩石围压卸荷量与渗透率关系

由图12可知，当采深=648 m时，围压卸荷量由0增加至51.43%，/仅由1增加至3.30，/近似线性增加；而>51.43%后，/由3.30骤然增加最大值24.71，呈非线性突变增加；当=85.71%时，试件完全破坏，但/略有降低，试验后检查发现试件内部渗入液压油，试件破坏导致其密封失效使得液压油渗入，并造成/降低。当=796 m时，≤51.16%，/近似线性增加；>51.16%时，/也出现了突变增加。当=944 m时，由0增加至19.61%，/由1增加至2.96，增加缓慢；而>19.61%后，/快速增加至10.08，试件破坏时仅27.45%。且随采深增加，/发生突变增加的围压卸荷量明显降低，即深部开采仅需较小的围压卸荷量便可导致其渗透率突变增加。

与图11(a)对比知，随围压卸荷量增加，不同采深下/均出现了非线性增加；围压卸荷量较小时，均为近似线性增加，而围压卸荷量增加至一定值后，/均骤然突增；且采深越大，/突变的围压卸荷量均越小。因此，岩石试件围压卸荷与渗流关系的试验结果与第3节理论分析一致，试验很好证明了不同采深下岩体围压的卸荷量与其渗透率比值的非线性突变增长关系。

结合赵固一矿煤样的力学参数=2.5 MPa，=0.7，令为岩石试件接近屈服状态的轴压峰值，计算了不同围压下岩石试件的(表1)，将渗透率测试的渗透压力差代入式(19)，计算得到了围压卸荷-渗流过程中TU-4，TM-2，TM-3试件的围压卸荷量临界值分别为60.80%，53.34%，57.14%，并将其用粉色虚线标注在了图12中。分析发现，试件TU-4，TM-2的围压卸荷量临界值均位于其渗透率突变阶段，在达到围压卸荷量临界值前的测点/近似线性增加，而大于等于围压卸荷量临界值的测点/骤然突增。结合式(15)，(18)，(22)及图11知，当小于围压卸荷量临界值时，随增加，岩体内围压卸荷-渗流产生的拉应力ΔT或ΔT线性增加，/近似线性增加；而当增加至大于等于围压的卸荷量临界值时，ΔT，ΔT继续增加并达到拉破裂的临界值，试件内拉破裂产生，/才出现了骤然突增。即由于围压的卸荷-渗流作用两试件产生了拉破裂，并造成试件的渗透率发生突变，岩石试件围压的卸荷量临界值便为其渗透率突变点；且渗透率突变点在岩石试件完全卸荷破坏之前，尤其TU-4试件最为明显，其渗透率先突变增加，后围压继续卸荷岩石试件才完全破坏使得渗透率仍很高。而TM-3试件/产生突变的临界值57.14%远高于其完全卸荷破坏的卸荷量27.45%，故在其完全卸荷破坏时，试件内部并未产生卸荷致拉破裂，试件由于轴向压应力作用首先产生了压剪破裂，轴向压剪破裂的临界值低于围压卸荷致拉破裂的临界值，同样造成了TM-3试件渗透率的非线性增加。故岩石试件围压的卸荷-渗流作用使得其内部拉应力不断增加，当拉应力高于试件自身围压限制及裂隙结构抗拉强度时，试件内部将产生拉破裂，并导致其渗透率突变增加，从而验证了前述深部开采岩体卸荷-渗流的致拉破裂机制。

同时，统计了不同初始围压下岩石试件破裂的应力特征(表1)及其破坏特征(图13)。

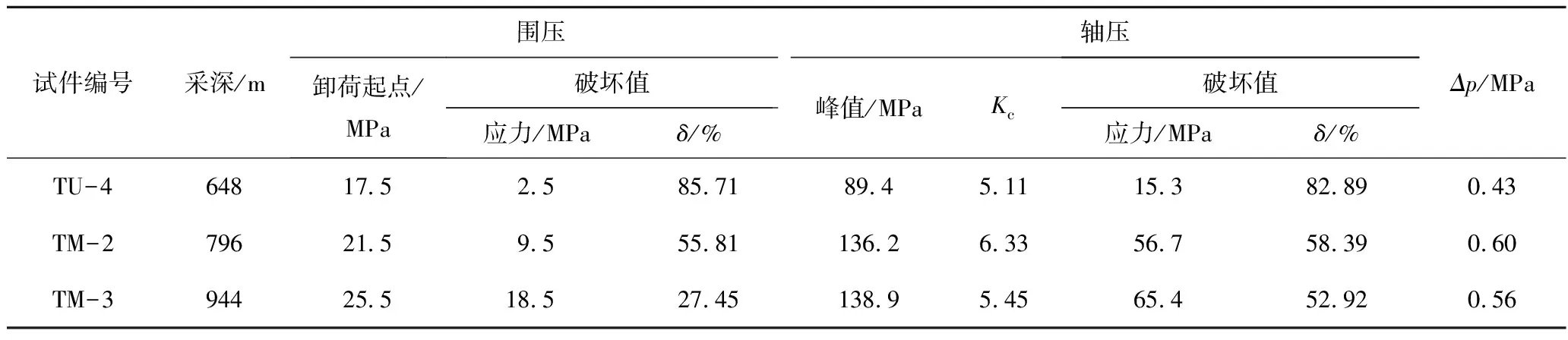
表1 不同初始围压下岩石试件卸荷-渗流致裂应力特征

图13 不同初始围压下岩石试件破坏特征

根据表1，随初始围压增加，即采深增加，试件接近屈服状态的轴压峰值增加，围压卸荷导致岩石破坏的轴压和围压值相应增高，但试件破坏时根据式(18)计算的和卸荷量降低。试件TU-4破坏时由17.5 MPa卸荷至2.5 MPa，由89.4 MPa 卸荷至15.3 MPa，，分别卸荷了15.0，74.1 MPa，卸荷85.71%，卸荷82.89%；而试件TM-3破坏时由25.5 MPa卸荷至18.5 MPa，由138.9 MPa卸荷至65.4 MPa，，分别卸荷了7.0，73.5 MPa，卸荷27.45%，卸荷52.92%。因此，采深增加，试件围压卸荷导致破坏的围压卸荷量显著降低，即采深越大，岩石仅需较小的围压卸荷量即可发生破坏。

由图13可知，当轴压加载至试件接近屈服状态再卸围压时，试件破裂面与轴向呈一定倾斜角度而出现整体剪切破裂，故在轴向高应力压剪、围压和围压卸荷三重因素作用下，试件仍呈剪切破裂特征，难以产生与卸荷方向一致的完全拉破裂失稳，但岩石围压卸荷导致的渗透率突变仍可诱发岩体突水等灾害发生。

因此，随围压增加，岩石试件产生卸荷-渗流致拉破裂或剪切破裂的围压卸荷量均显著降低，岩石试件围压的卸荷-渗流致拉破裂将导致岩石渗透率突变增加，且采深越大，渗透率突变点的围压卸荷量越小，进而从试验角度验证了前述深部开采岩体的卸荷-渗流致拉破裂机制及其与渗流的关系，以此可判定深部开采卸荷岩体的稳定性。

5 讨 论

笔者基于深部岩体内裂隙的单一尺寸因素研究了裂隙对岩体围压卸荷-渗流致裂的影响，并不特指某种具体形状的裂隙，强调了由于该裂隙的存在导致围压卸荷-渗流过程中岩体内拉应力及渗透率发生变化，可用于解释卸荷-渗流过程中岩石试件或岩体整体未失稳，而卸荷至一定程度时渗透率却发生了突变增加的现象，也可解释岩石卸荷初始阶段具有声发射信息，卸荷至一定程度时声发射信息积聚现象。

同时，受轴向应力影响，在岩石卸荷-渗流过程中，岩体围压可能未卸荷至拉破裂阶段(试件TM-3)，岩体已完全破裂；如岩体足够大时围压卸荷，在轴向应力压剪作用下，岩体也极易因符合裂隙面强度理论而产生剪切破坏，沿裂隙面产生剪切破裂的条件为

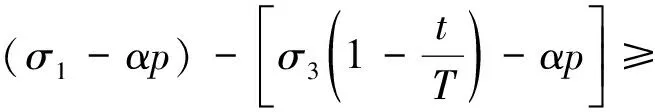
(24)

式中，，分别为裂隙面的黏聚力和内摩擦角；为与裂隙面法线方向的夹角。

联立式(18)，并将=，=代入，则式(24)可简化为

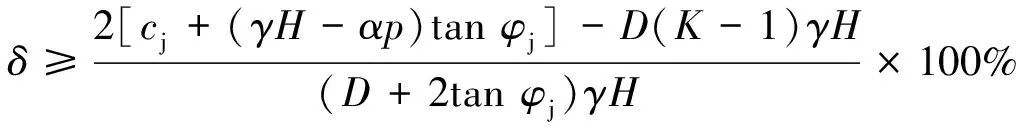
(25)

式中，=(1-tancos)sin 2。

式(25)中，岩体是否发生剪切破裂取决于变量，，，，，；当=0时，式(25)退化为卸荷前的应力状态，即岩体承受压应力作用而未发生剪切破坏。为分析岩体围压卸荷-渗流过程中剪切破裂与拉破裂的关系，根据图1拟合曲线计算，设=45°，=3，按岩体强度最低值计算，=45°+/2，以的变化为例(分别令=5.0，15.0，45.0 MPa)，计算分析岩体剪破裂时所需的卸荷量临界值，并分别将其与图9(a)中=1时的拉破裂卸荷量临界值对比，如图14所示。

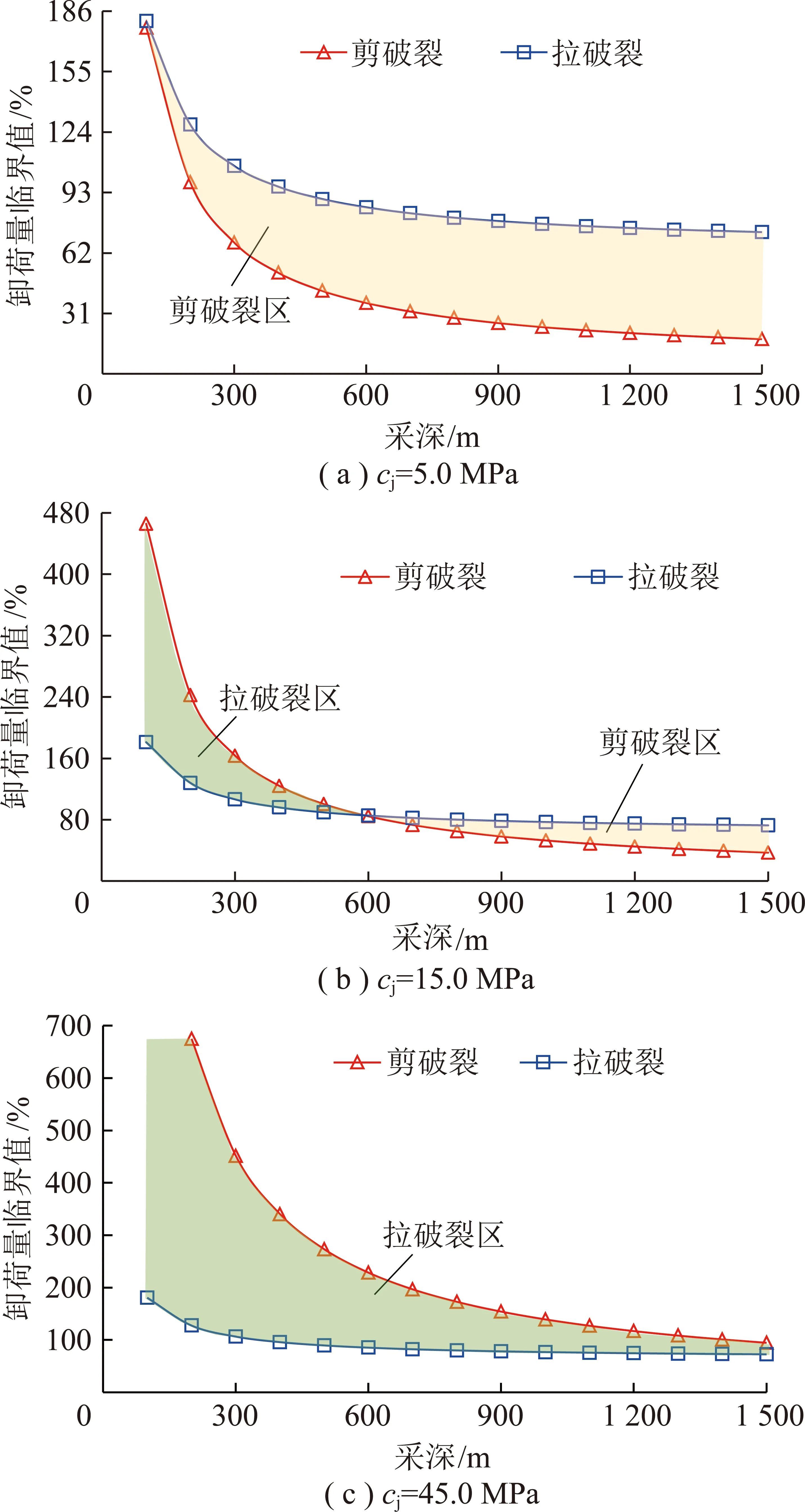
图14 不同采深岩体围压卸荷-渗流致拉破裂与剪破裂关系

根据图14，随采深增加，岩体卸荷-渗流产生剪切破裂所需的卸荷量临界值变化规律与拉破裂相同，均非线性降低；采深较小时，卸荷量临界值快速降低；采深较大时，则近似线性降低。根据式(19)及式(25)知，这是由于采深增加，岩体的抗拉强度和抗剪强度并未增加，但围压显著升高，且岩体内裂隙附近应力集中和压应力的增加速率均远高于围压的升高速率所致。

同时，深部岩体卸荷-渗流是否发生拉破裂或剪切破裂与的大小密切相关。当较小时，岩体卸荷-渗流致拉破裂所需的卸荷量均高于剪切破裂，并导致剪切破裂首先发生，岩体剪切破裂区分布广泛。若增加，岩体剪切破裂所需的卸荷量临界值增高，并造成浅采深岩体拉破裂的卸荷量临界值低于剪切破裂，使得浅采深岩体将由剪切破裂向拉破裂转变，大采深时则相反，并由此形成了浅采深岩体拉破裂区与大采深岩体剪切破裂区交叉分布的形式，如图14(b)所示。当较大时，岩体卸荷-渗流致拉破裂所需的卸荷量均低于剪切破裂，并导致拉破裂首先发生，拉破裂对岩体破坏的影响增高，岩体内拉破裂区将广泛分布。

且当较大时，岩体围压卸荷-渗流产生剪切破裂所需的卸荷量临界值远高于100%，即使岩体围压卸荷至0甚至拉应力时，剪切破裂也不可能产生，则岩体内将只发生拉破裂，而不会发生剪切破裂；由此也可能导致室内卸荷试验时，岩石试件渗透率突变，但试件并未发生整体的宏观失稳现象。在此种情况下，若拉破裂产生所需的卸荷量临界值也高于100%，即岩体围压卸荷至0时，拉破裂仍不会发生，由此也可能导致室内卸荷试验时，岩石试件渗透率并不会发生突增现象。

而由于煤系地层岩体内部包含大量孔隙、微裂隙、节理、层理、断层等不同尺度、角度或开度的裂隙结构，并呈非均匀性分布，其对岩体围压的卸荷-渗流致裂均产生影响，这使得岩体拉破裂的形成机制产生变化，故不同裂隙结构岩体卸荷-渗流致拉破裂的发展过程及其与断裂力学的联系亟待进一步研究。

6 结 论

(1)围压卸荷-渗流过程中，深部裂隙岩体内产生了与卸荷方向平行的附加拉应力Δ；Δ随采深和承压水压力增加而增大；且随卸荷-渗流总时间增加，Δ峰值先快速下降后缓慢降低；岩体内裂隙尺寸越大，Δ峰值越高。

(2)深部岩体卸荷-渗流致拉破裂的条件为Δ克服其自身围压及裂隙结构抗拉强度之和Δ；在卸荷-渗流总时间影响下，Δ≥Δ，则岩体卸荷-渗流产生拉破裂，否则无拉破裂产生。同时，计算获得了不同采深岩体围压卸荷-渗流致拉破裂的卸荷量临界值变化规律，并指出：卸荷量临界值随采深增加先非线性快速降低后近似线性降低；且承压水压力越高，卸荷量临界值越低。

(3)基于Bandis双曲线裂隙变形公式，获得了卸荷作用下裂隙岩体的渗透率变化规律，发现了裂隙岩体渗透率的非线性突变点即为卸荷-渗流致拉破裂的卸荷量临界值，且采深及承压水压力越大，岩体渗透率突变点的围压卸荷量越小。

(4)开展了不同初始围压下岩石的围压卸荷-渗流试验，验证了深部开采岩体围压的卸荷-渗流致拉破裂机制及其与渗流的关系和渗透率突变点特征；对比分析了岩体拉破裂与剪切破裂的关系，并指出：受裂隙岩体结构及属性参数影响，拉破裂的卸荷量临界值可高于或低于剪切破裂；随采深增加，岩体可由剪切破裂向拉破裂转变。