煤矿井下全空间地震波时频域极化分析及其试验研究

王 勃，曾林峰，张 衍，刘盛东，章 俊，陈泓云

(1.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221116；2.中国矿业大学 资源与地球科学学院，江苏 徐州 221116；3.中国矿业大学 力学与土木工程学院，江苏 徐州 221116；4.深地科学与工程云龙湖实验室，江苏 徐州 221116)

“双碳”目标下我国能源资源禀赋特征及当前复杂国际能源形势，决定了煤炭在能源中的基础和兜底保障作用。煤炭绿色开采、智能精准开采等对煤矿安全高效开采地质保障系统提出了更高的要求，矿井地质透明化是当前矿井地质保障系统发展的努力方向。矿井地震勘探具有不受复杂地面条件影响、距离目标体近、地震波能量和高频成分衰减少、分辨率高、探采对比易验证等优点，进而被广泛运用于地质精细探测及透明地质建模。

不同于地面半空间地震勘探，矿井地震属于全空间条件下勘探。震源在井下激发后，地震波向四周传播，检波点会接收到全方位的地震信号。单分量信号难以确定地震波的方向，双分量地震信号仅能算出二维平面上地震波传播方向，三维空间条件下准确判定地震波传播方向则依赖三分量信号的矢量特性，并通过极化分析实现。极化分析在地震信号处理中主要用于波场分离，根据各类地震波的极化属性差异设置滤波器来分离提取有效波。极化滤波方法在天然地震、石油地震勘探领域研究较多，DIALLO 等对多分量地震数据进行小波变换，将自适应瞬时极化滤波引入时频域，进行面波压制及转换波分离。KULESH 等提出了基于自适应协方差矩阵的小波域时频极化分析方法，在时频域实现了波场分离。PINNEGAR采用S变换在时频域计算三分量地震信号极化参数，设置极化率滤波器压制极化椭圆性地震波。程冰洁等在小波域进行能量分类约束从而实现极化滤波。

在煤炭领域，张平松等在时间域构建协方差矩阵，采用极化滤波方法实现了巷道超前探测多波有效分离。王勃利用三分量信号的矢量特征，提出了一种全空间条件下集波场分离、偏移成像于一体的极化偏移方法。胡泽安等在时间域对矿井槽波地震数据进行了极化分析，实现了波场分离与噪声压制。金丹等利用槽波信号与干扰波在偏振度上的差异，改进频率域的极化滤波权函数，将频率域极化滤波用于槽波记录的噪声压制。冯磊等对二分量槽波数据进行S变换，采用时频域自适应协方差矩阵极化滤波方法实现了两类槽波分离。刘盛东等利用三分量地震记录，通过时窗自适应的极化分析方法获取极化率，提取了纵横波及勒夫型槽波等线性极化波。

上述方法主要用于地面半空间或煤矿井下全空间的极化滤波，针对矿井全空间条件下三分量地震波传播方向研究较少，特别在矿井地震近场勘探多类型波场混叠条件下。笔者提出了一种矿井全空间三分量地震波时频域极化分析方法，首先通过时间域混叠合成信号验证地震波优势方位角、倾角准确度，然后开展全空间条件下中心激发-全方位接收的三维三分量数值模拟实验对比纵波、横波定向精度，最后通过矿井地震勘探常用的反射波现场试验验证极化参数求解的可靠性。

1 全空间地震波时频域极化分析方法

矿井地震属于全空间条件下近场勘探，多类地震波混叠，需从时间、频率2个维度联合计算分析。为准确计算地震波传播方向，笔者首先构建基于基本小波函数形态不固定的广义S变换的时频域复协方差矩阵，然后求解三分量地震信号的优势能量方向。同时，为进一步验证方向计算的准确性，开展已知震源点聚焦定位对比研究，具体理论方法如下。

1.1 基于广义S变换的时频域复协方差矩阵构建

设时间域信号()的傅里叶变换为

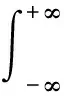
(1)

式中，j为虚数单位；为频率；为时间。

对时间序列()乘以一个窗函数()得

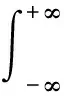
(2)

设()为归一化的高斯窗，且利用参数控制其时窗宽度，利用参数控制其时窗位置，则有

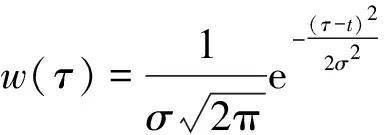
(3)

将式(3)代入式(2)，可得到对时间序列()在时刻加高斯窗的谱为

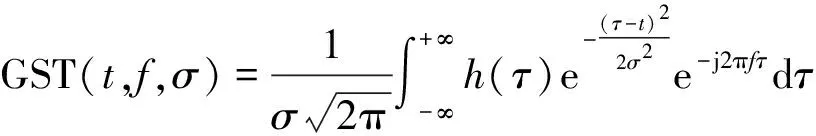
(4)

将窗宽控制参数设置成与频率成反比的关系，以此让高斯窗的宽度自适应于频率，则有

(5)

和为控制时窗宽度变化的2个参数，进一步获得广义S变换的表达式为

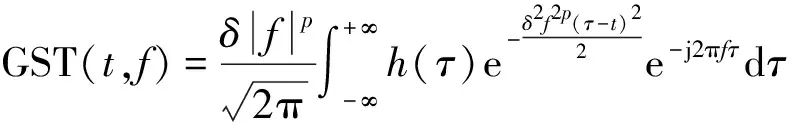
(6)

通过广义S变换计算时频谱，再利用Hilbert变换构建时频谱的解析信号。在时频域内时刻，频率处的复协方差矩阵(,)可描述为

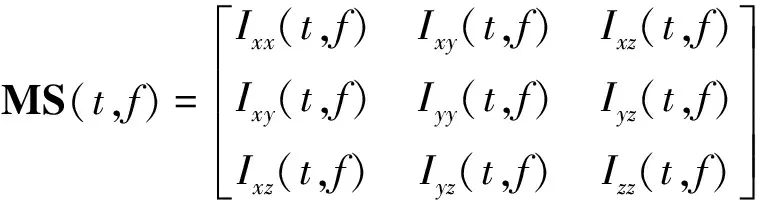
(7)

矩阵中各元素定义为

(8)

式中，|SC(,)|和|SC(,)|为2组解析信号的瞬时振幅；和为瞬时频率；arg为瞬时相位；(,)为均值，其定义为

(,=,,)

(9)

式中，R(·)为复数的实部，函数sin()为辛格函数，其定义为

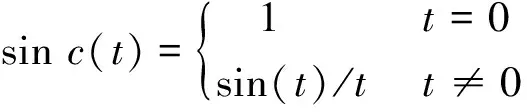
(10)

(,)为自适应时窗长度，其定义为

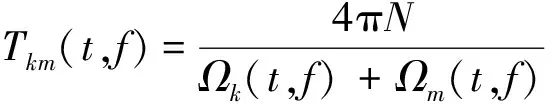
(11)

式中，为整数，是一个经验参数，用于刻画不同极化属性，取较大值时可刻画三维复杂极化属性,一般取1或2。

当3个分量时频谱中对应时频点的瞬时频率相等时，(,)=(,)=(,)，(,)可简化为2π(,)，复协方差矩阵可以化简为

(,)=|SC(,)||SC(,)|×

cos[arg SC(,)-arg SC(,)]=

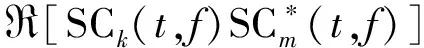
(12)

式中，为复共轭。

1.2 极化参数计算

地震波矢量特征可以用极化参数描述，这些参数可以通过在时频域中求取复协方差矩阵的最大特征值及其对应的归一化特征向量(,,)获得。

优势极化方位角计算公式为

()=arctan[R()R()]

(13)

其中-90°≤()≤90°，为极化主轴在面的投影与轴的夹角，当极化主轴偏向轴正方向时，()>0°；当极化主轴偏向轴负方向时，()<0°。

优势极化倾角计算公式为

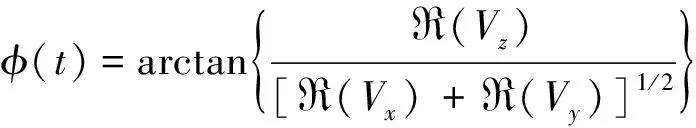
(14)

其中，-90°≤()≤90°，为极化主轴与面的夹角，当极化主轴偏向轴正方向时，()>0°；当极化主轴偏向轴负方向时，()<0°。

1.3 聚焦定位方法

与微震定位不同，地震勘探震源点位置已知，为了验证上述极化参数准确性，利用检波点位置及其极化倾角、方位角反向求解震源点位置，其计算方法如下：设检波点的空间坐标和主极化轴归一化矢量分别为=(,,)和=(,,)，设空间任意一点=(,,)。向量与向量的向量积代表向量和向量共起点的情况下所构成平行四边形的面积。对该向量积除以空间矢量的模可获得点到空间矢量的最短距离：

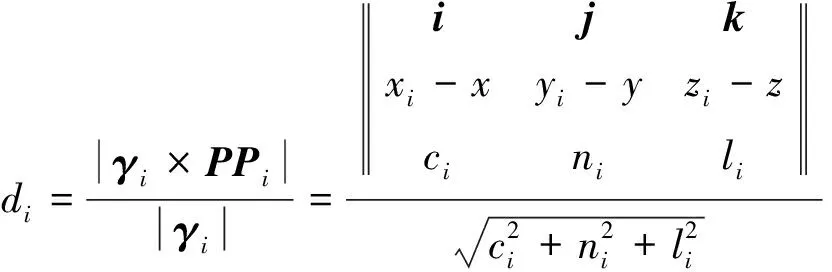
(15)

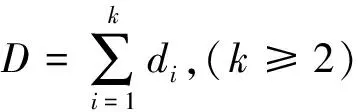
(16)

求取的最小值所对应的(,,)为震源点在三维空间内的位置。

2 三维数值模拟及算法验证

2.1 合成信号及极化特征分析

为了验证极化分析对三分量信号在时频域上区分多类型波和计算极化参数的准确性，开展正弦波合成信号分析实验。合成信号由A,B,C,D,E,F共6个信号组成，合成信号具体参数见表1。其中B，C信号在时间域混叠，E，F信号在时间域混叠，在时间域可分为4段信号，如图1所示。其中每组信号均为501个采样点，采样频率为2.5 kHz，对合成信号进行时频域极化分析，结果如图2所示。时频谱上可清晰区分A，B，C，D，E，F信号，图2(a)显示的6个信号的方位角与理论方位角一致，正、负方位角均无误差；图2(b)显示的6个信号的倾角与理论倾角一致，正、负倾角均无误差。

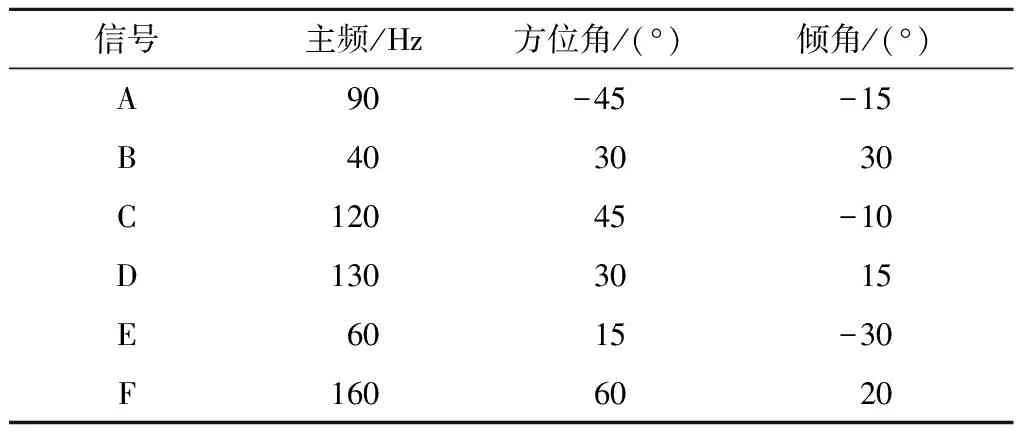
表1 合成信号基本参数

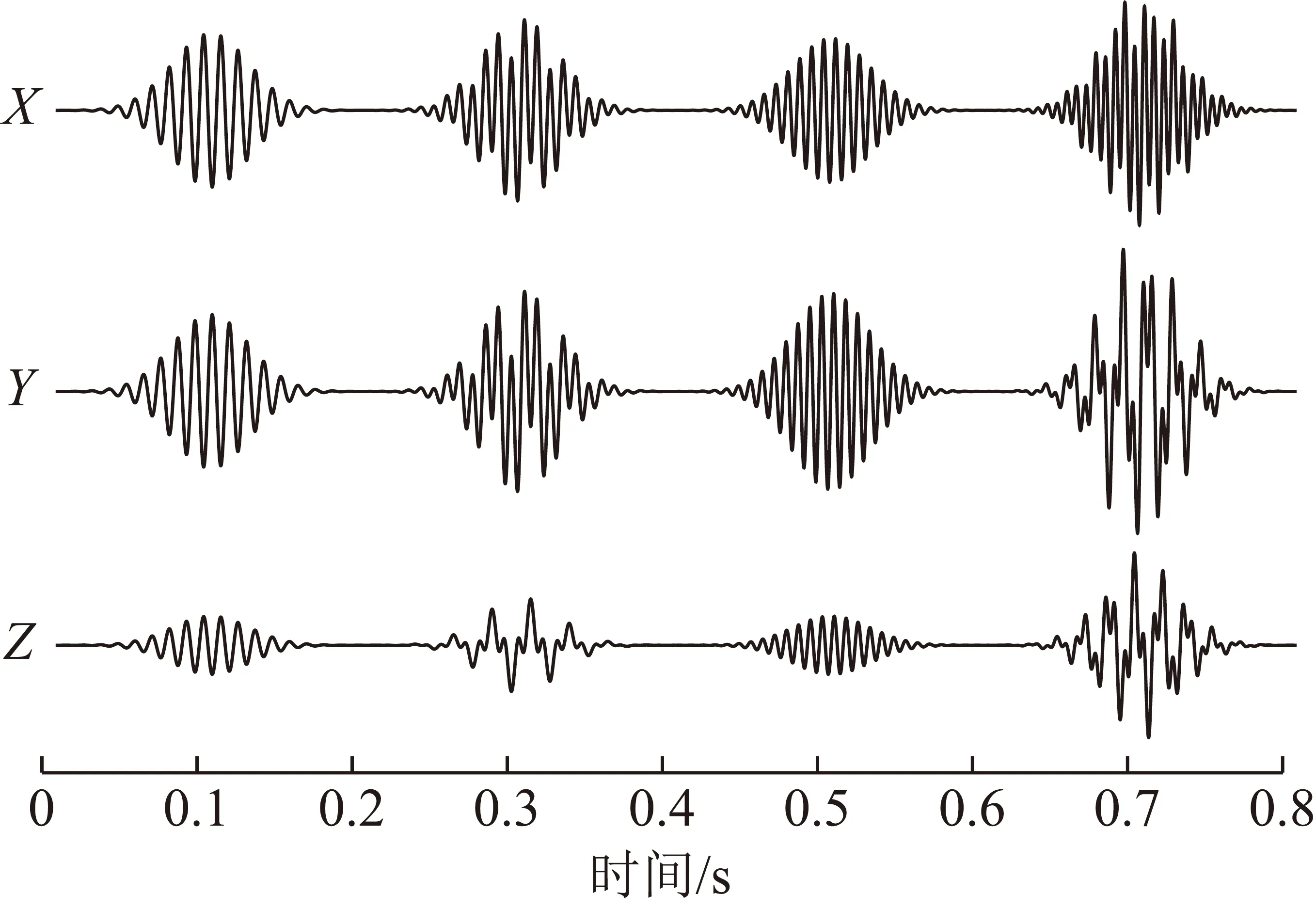
图1 合成三分量信号

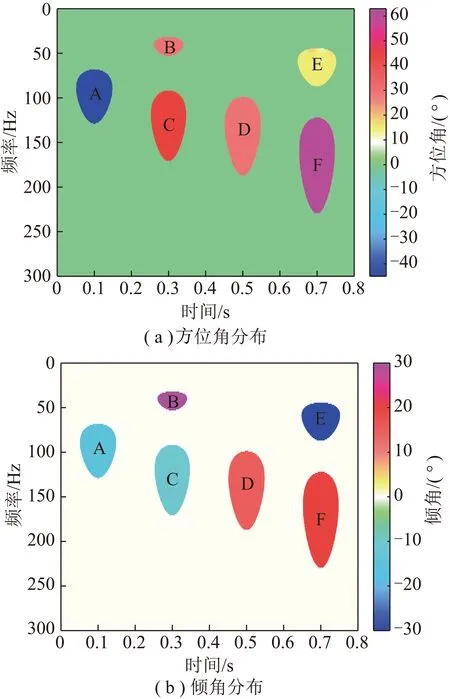
图2 合成三分量信号方位角及倾角分布

2.2 正演模拟信号极化特征分析及聚焦定位验证

为研究全空间条件下地震波矢量特征，建立三维数值模型。模型中心为震源点，在震源点的左侧、右侧、前方、后方、顶部及底部布置检波器，形成中心激发全方位接收的三维三分量地震观测系统，如图3所示。三维模型在,,方向的大小分别为400 m×400 m×400 m，震源点位于(0，0，0)原点处，三分量检波器在,,面上以原点为中心直径为200 m的圆形测线上以15°间隔布置，累计66个检波器。模型在,,方向上进行网格化，网格间距均为0.3 m。模拟采用主频为125 Hz的零相位雷克子波，采样频率为2.5 kHz。模型添加PML吸收边界，采用三维时空域高阶有限差分法进行数值模拟。

图3 三维观测系统

在数值模拟地震数据中选择一道(第64道)数据进行时频域极化分析，通过对比理论、计算的极化参数验证上述方法效果。利用直达波的理论到达时间、震源主频确定直达波的时频范围，在图4中可分析直达纵波、横波的极化参数，从图5可见直达纵波、横波质点振动轨迹。图4为第64道数据求得的极化方位角、极化倾角。由图4(a)可看出，在时间0.03 s 和0.06 s附近各有一团能量，分别为纵波、横波能量。直达纵波、横波的方位角均为3.3°，与理论值0°存在部分偏差。由图4(b)可看出，时间0.03 s附近的直达纵波倾角为45°，与理论值45°无偏差。时间0.06 s附近处的直达横波倾角为-45°，与理论值-45°无偏差。计算其他65道地震波时频域极化参数，并利用直达纵波的极化信息对震源点进行反向聚焦定位，结果如图6所示，在200 m直径范围内，求解震源点与已知震源点的直线距离误差仅为 0.548 6 m。

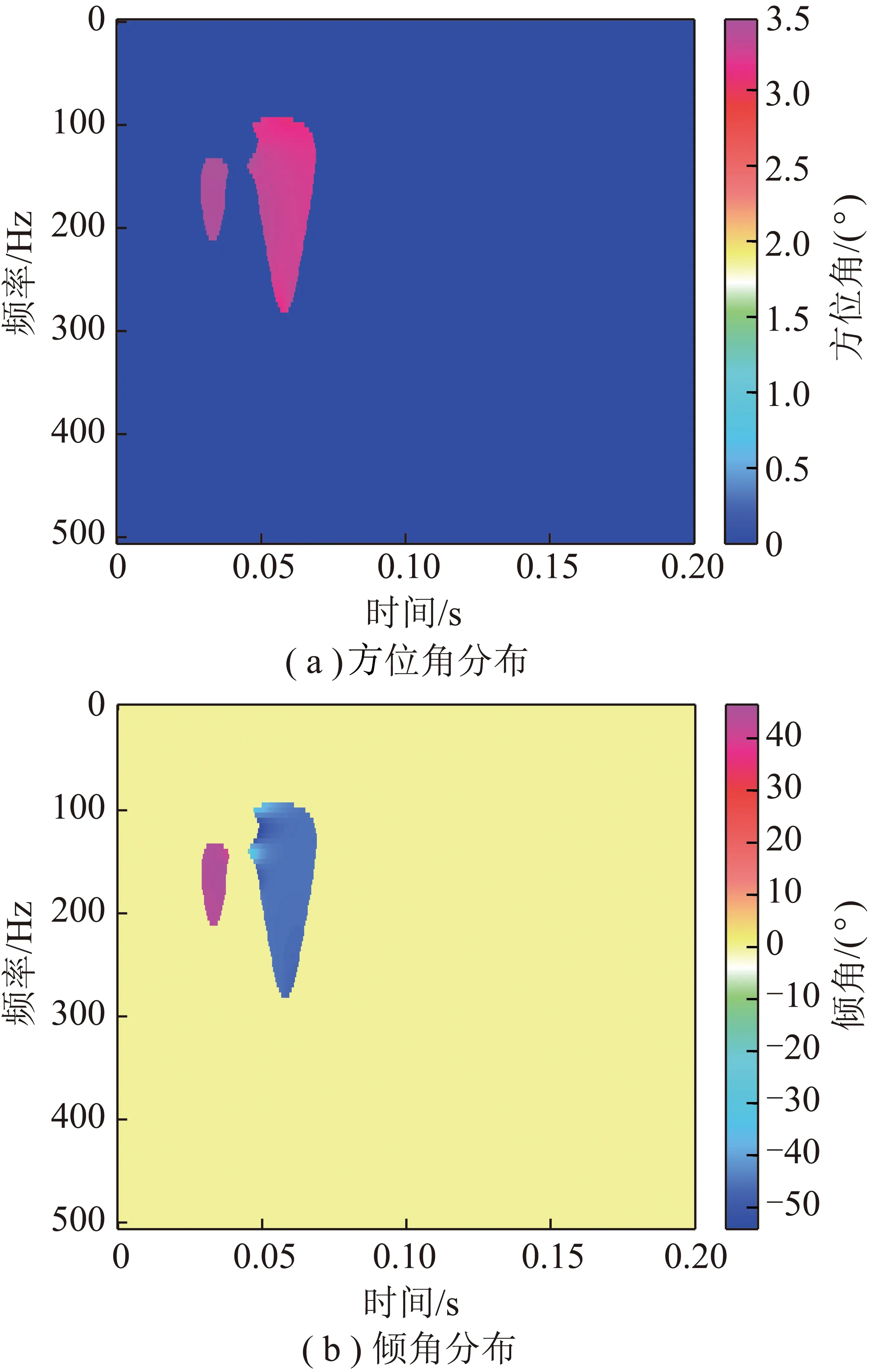
图4 计算所得极化方位角与极化倾角

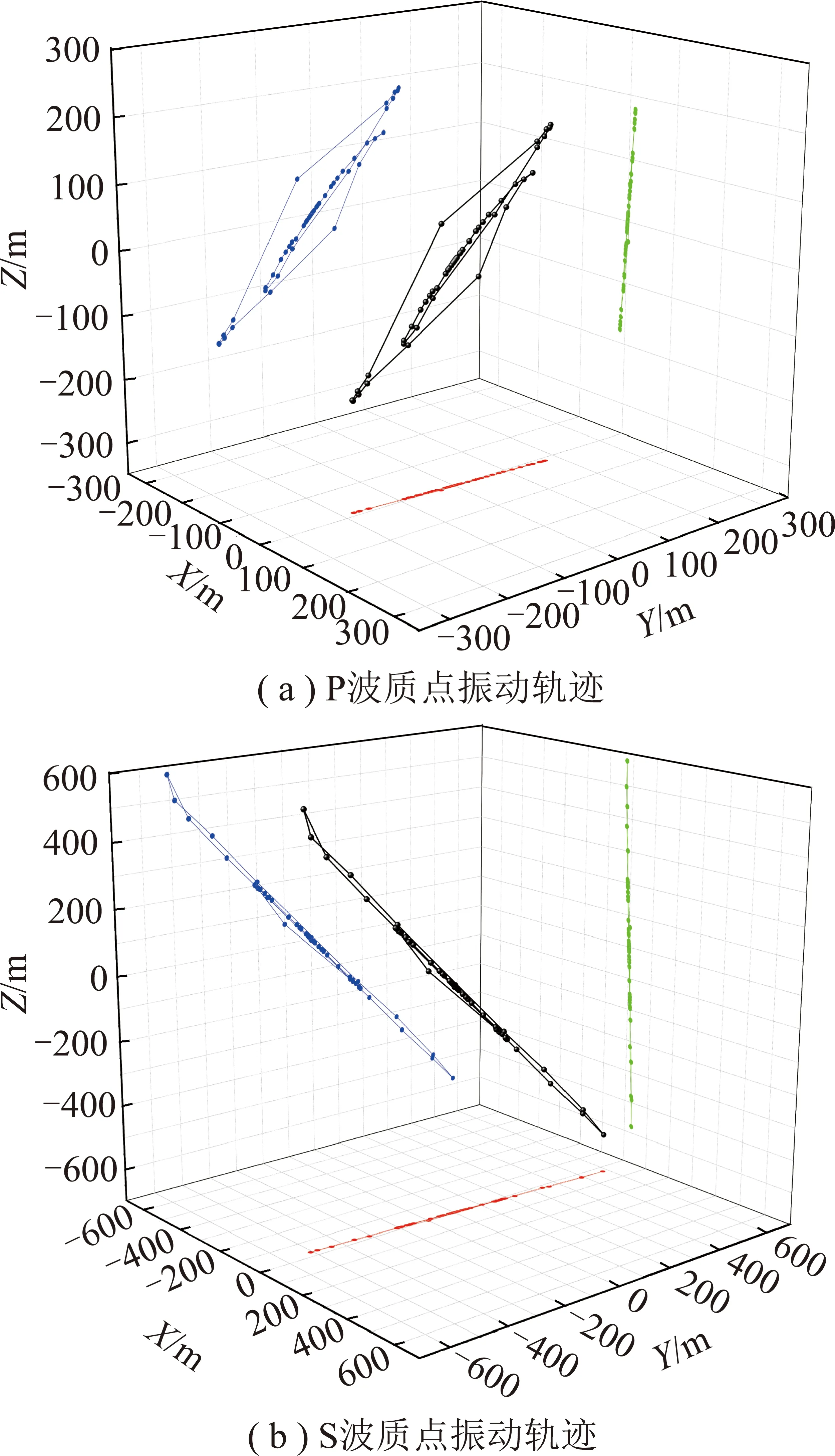
图5 第64道三分量信号质点振动轨迹

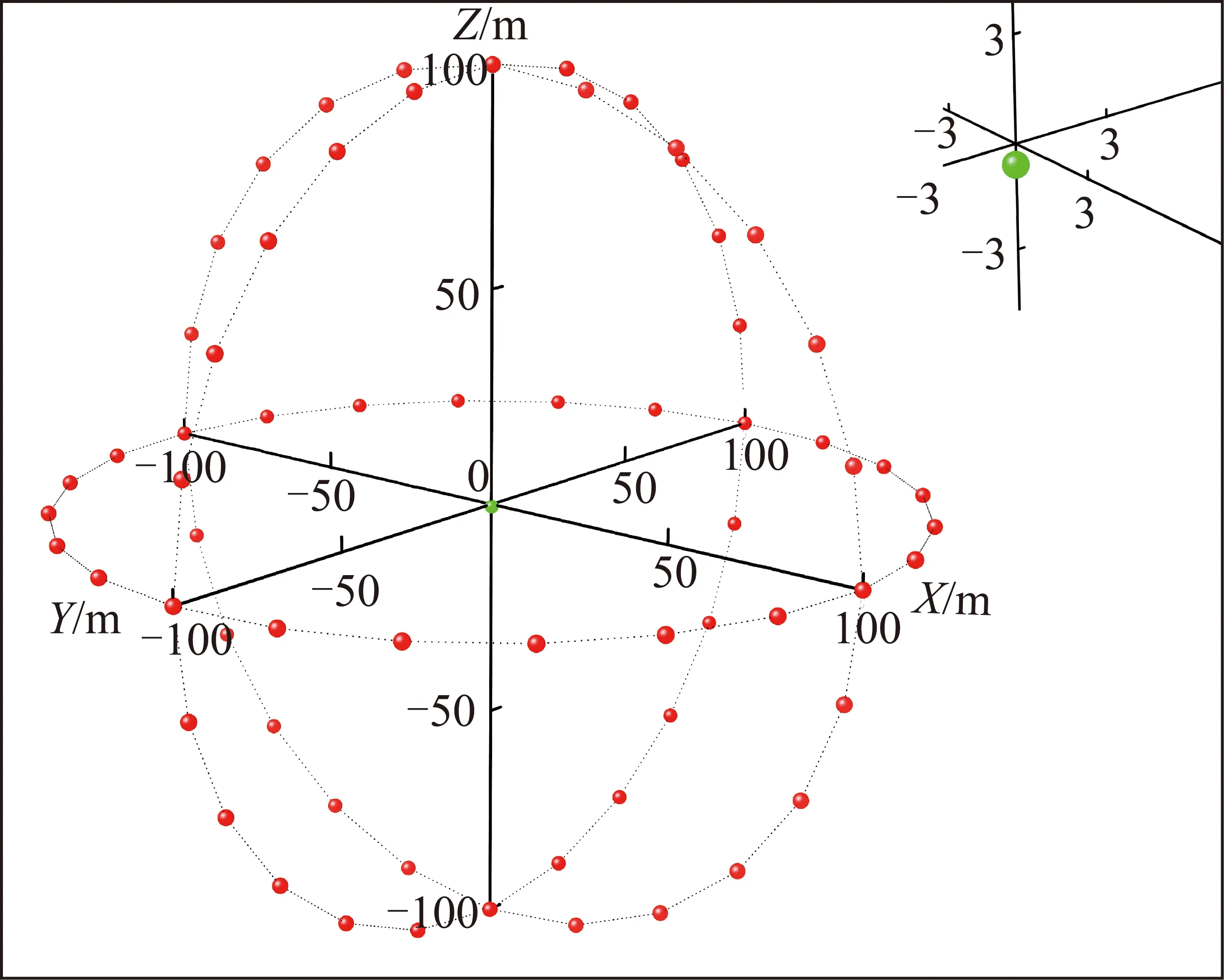
图6 检波点反向聚焦定位震源点(右上角为原点位置局部放大)

3 现场试验

实际矿井地震勘探过程中，除利用透射波之外，还常采用反射波，特别是煤层条件下反射槽波勘探是井下通用方法。为此，开展了现场实测并针对反射槽波信号进一步验证方法有效性。

安徽某矿1034工作面位于三采区深部，煤层顶板标高-603.8～-466.0 m，煤厚3.0～5.2 m，平均3.9 m，煤层倾角5°～18°，平均10°，顶板为灰白色中粒砂岩，底板为粉砂岩。1034回风巷外帮发育有F13正断层，与回风巷相距57～108 m，走向NE，倾向NW，倾角60°～70°，落差100～200 m，其在矿区内延展长度5.20 km，利用地面、井下钻探进行断层探查，断层控制程度可靠。以R1检波点为原点，每隔10 m布置1个检波点，震源点设置在132.5 m处，三分量地震勘探观测系统如图7所示，S1炮激发R1～R27道接收的三分量地震记录如图8所示。

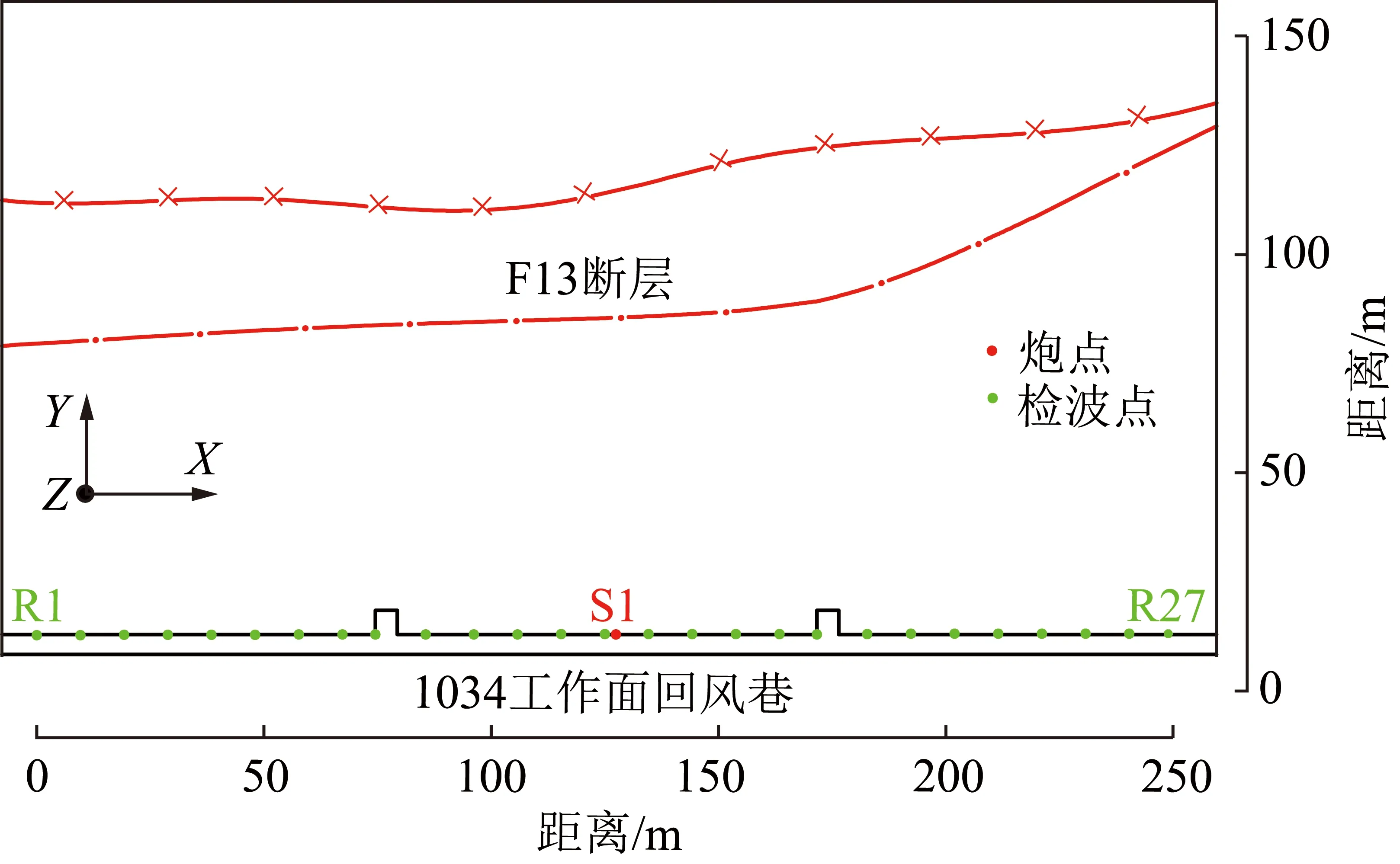
图7 某矿1034工作面地震观测系统

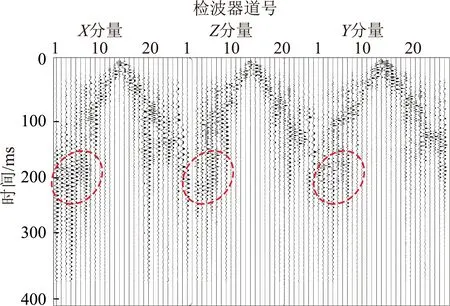
图8 三分量地震记录

观察三分量地震记录，图中红圈处(R1～R8道记录)存在明显反射槽波信号。选取R4道进行分析，S1炮、F13断层与R4检波点的反射路径距离约213.28 m，R4检波点接收的反射槽波理论方位角约为27°，倾角则等同于煤层倾角，约10°。S1炮激发、R4三分量检波器接收的地震信号进行时频域极化分析，时频域方位角及时频域倾角如图9所示。根据已知断层位置计算反射槽波理论传播路径，时间0.18～0.25 s、频率120～180 Hz区域为反射槽波。图9(a)中该区域的方位角计算结果可见，反射槽波的方位角较稳定，约为28°，分析其主要为Rayleigh型反射槽波，与理论方位角偏差1°。图9(b)显示反射槽波的倾角为10°～12°，与实际煤层10°倾角吻合。

图9 R4道数据时频域极化方位角倾角分布

4 结 论

(1)对三分量合成信号进行时频域极化分析，得到信号的时频位置与理论时频位置相对应，求解的方位角、倾角与理论值吻合；在时间和频率2个维度上，时频域极化分析可以精准确定混叠情况下多类型信号极化方向。

(2)针对中心激发-全方位接收的三维时空域高阶三分量模拟信号，直达波的方位角、倾角误差分别为3.3°，0°；在200 m直径范围内，根据检波点位置及地震波方位角、倾角聚焦定位的震源点与已知震源点的距离误差仅为0.548 6 m，验证了全空间条件下三分量地震波的时频域极化参数计算的精度。

(3)针对矿井实测数据进行广义S变换的时频域极化分析处理，反射槽波的时频域方位角、倾角参数与理论值一致，证实了矿井全空间三分量地震波时频域极化分析方法的有效性。

(4)全空间条件下时频域极化分析方法确定的地震波传播方向可为矿井地震勘探精细成像提供基础性支撑，并为井下地质构造的透射波层析成像、反射成像等提供基础约束条件。