煤体CO2吸附/解吸变形特征及变形模型

张遵国，陈 毅，唐 朝，马凯欣，张春华

(1.辽宁工程技术大学 安全科学与工程学院，辽宁 葫芦岛 125105；2.矿山热动力灾害与防治教育部重点实验室，辽宁 葫芦岛 125105)

煤层CO地质储存与煤层气强化开采技术(CO-ECBM)不仅能提高煤层气采收率，还能起到CO地质封存的作用，是我国实现“碳达峰、碳中和”目标的重要手段。但煤体在吸附CO过程中会发生膨胀变形，导致渗透率减小，影响CO的可注性，进而影响CO封存和煤层气的驱替效果。由此可知，研究煤体CO吸附/解吸特征及变形特征对增强煤层CO可注性技术的发展和评价煤层CO封存技术的适用性意义重大。而我国煤炭种类繁多，不同煤阶煤体对CO的吸附能力及膨胀变形特征不甚相同，开展此方面的研究十分必要。

针对煤体吸附CO膨胀变形特征，国内外研究者开展了大量研究。贺伟等研究了不同煤阶煤样CO吸附特性及煤样吸附变形规律，发现CO吸附量随煤阶升高而增大，体应变量随煤阶升高而减小；而DURUCAN等通过开展煤样吸附CO变形试验，提出CO注入引起的基质膨胀对煤的渗透率有严重的影响，并发现煤的膨胀量随煤阶升高而增大，认为这与高煤阶煤较大的吸附量有关；张倍宁等则测量分析了CO注入储存过程中煤体膨胀变形特性，发现储存相同量的气态CO，贫煤的体积膨胀应变>弱黏煤>贫瘦煤。

为定量描述煤的吸附变形特征，业界学者建立了大量吸附变形模型。理论推导方面，吴世跃等根据表面物理化学和弹性力学原理，推导了煤吸附膨胀变形理论公式；郭平等、LIU H等基于吸附过程中煤的表面自由能变化等于煤体弹性能变化的基本假设，考虑煤样吸附膨胀作用以及气体压力对煤的压缩作用两方面因素，推导了煤体吸附膨胀变形表达式；但以上推导均是将煤视作各向同性的弹性体，符合胡克定律，且假定煤样的体积模量或弹性模量为定值。GUO X等、ZHANG X等则从煤的吸附膨胀特性着手，考虑煤样吸附量对于膨胀变形的影响，用吸附量乘以变形系数，得到了表征吸附膨胀与吸附量的关系模型，但他们均默认煤的变形系数为定值，即认为吸附膨胀与吸附量呈线性关系。试验研究方面，国内外学者则主要采用Langmuir方程描述煤样的吸附膨胀变形特征；刘延保在Langmuir方程基础上增加了煤样解吸过程的残余体应变，建立了改进的Langmuir方程，可以描述煤样解吸应变量与平衡压力的关系。

相关研究表明，原煤吸附/解吸气体变形具有明显的各向异性，且煤吸附气体后力学强度会显著降低，表现为弹性模量减小，与理论模型的假设条件不符。此外，WANG Z等通过试验研究提出煤的吸附膨胀与吸附量之间存在多项式关系，现有理论模型的适用性有待进一步研究。

纵观以上研究成果，吸附膨胀变形与煤阶的关系仍存在争议，且现有研究大多仅考虑了吸附过程的变形特征和变形模型，对解吸过程的变形特征和变形模型的研究较少，针对煤样吸附/解吸变形特征以及变形模型还需进一步研究。鉴于此，笔者利用自行研制的煤层高压吸附/解吸(变形)试验系统，开展了3种不同煤阶原煤等温吸附/解吸CO过程中吸附量与变形量同步测试试验，分析了煤体吸附/解吸CO变形特征及煤体应变与吸附量的关系，建立了应变量-吸附量关系模型以及煤样吸附/解吸CO变形模型，探讨了不同煤阶煤CO可注性及CO封存技术的适用性。

1 试验方案

1.1 试验煤样

煤样分别取自山西省沁水煤田潞安矿区常村煤矿3号煤层(属古生界二叠系下统山西组)、黑龙江省鹤岗矿区峻德煤矿17号煤层(属中生界白垩系下统石头河子组)、辽宁省南票矿区小凌河煤矿主采煤层(属古生界石炭二叠系含煤地层)，各煤样工业分析结果见表1。

表1 试验煤样工业分析结果

利用取心机将现场取回的煤块沿垂直层理方向钻取出25 mm的煤心，采用切割机把煤心加工为尺寸约25 mm×50 mm的煤样后，再用砂纸把煤样端面打磨平整，制得不同煤阶原煤试样各3个，如图1所示。为尽可能减小相同煤阶煤样之间的差异性，同种煤阶的煤样均取自同一煤块，且为排除水分差异对试验结果的影响，加工好的煤样均放入烘干箱以75 ℃烘24 h以上直到煤样1 h内质量不变，认为煤样被烘干，然后开展后续试验。

图1 试验煤样

1.2 试验装置

如图2所示，试验利用自主研制的煤层高压吸附/解吸(变形)试验系统，通过高压容积法测定煤样吸附量，通过电阻应变计测定煤样变形量，从而实现煤样吸附量和变形量同步测试功能。

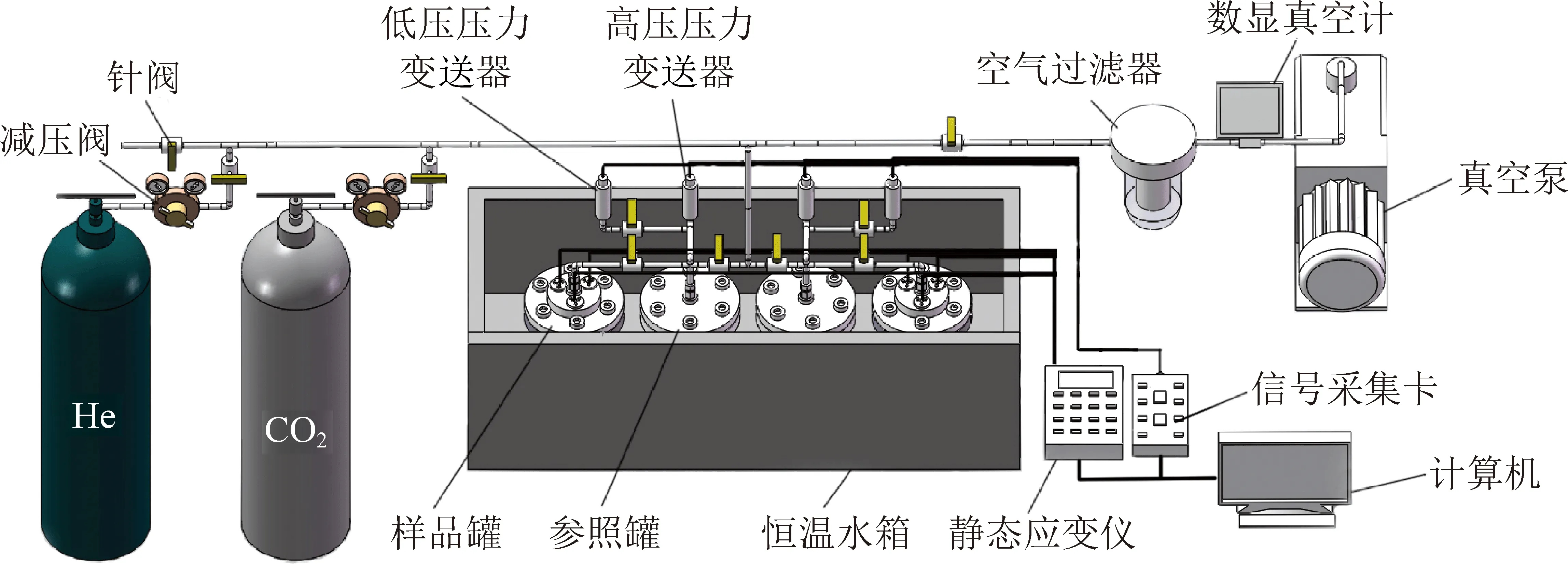
图2 试验系统原理

1.3 试验流程

吸附/解吸试验参照GB/T 19560—2008《煤的高压等温吸附试验方法》进行。首先设置试验温度为30 ℃，将煤样置于样品罐中，抽真空24 h以上，然后采用高纯度He(体积分数99.99 %)标定自由空间体积。

采用高纯度CO(体积分数99.99 %)作为吸附质，按照加压—平衡—加压过程，逐级提高气体压力进行吸附，当达到最高试验压力后按照降压—平衡—降压过程逐级降低气体压力进行解吸。试验过程中实时采集气体压力数据，并依据试验测得的煤样质量和试验过程中采集的气体压力数据计算不同平衡压力下煤样的CO吸附/解吸量。

试验过程中，由于煤样不同和吸附平衡压力不同，达到吸附平衡压力的时间也不同。当30 min内气体压力波动小于传感器测量精度(0.01 MPa)时，认为煤样达到吸附平衡状态。一个试验压力达到平衡历时12～48 h不等，升压吸附—降压解吸全过程试验周期为12～18 d。

此外，通过在制好的各原煤侧面中部光滑无明显裂纹处垂直粘贴2个电阻应变计，分别测定试验过程中煤样的纵向应变和横向应变。

2 试验结果与分析

2.1 等温吸附/解吸特征

试验得到煤样CO等温吸附/解吸曲线如图3所示，图3中实线为等温吸附曲线，虚线为等温解吸曲线。

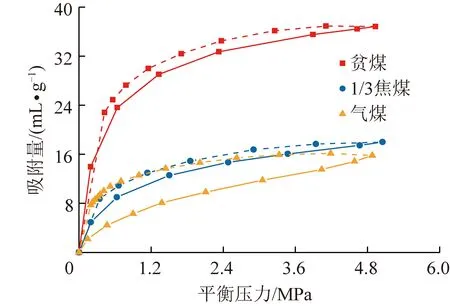
图3 煤样等温吸附/解吸曲线

已有研究表明，基于微孔填充理论的D-A方程对CO等温吸附数据的拟合精度最高，更适用于解释煤中CO的吸附行为。因此，采用D-A方程(式(1))对各煤样CO等温吸附/解吸数据进行拟合，拟合结果见表2。

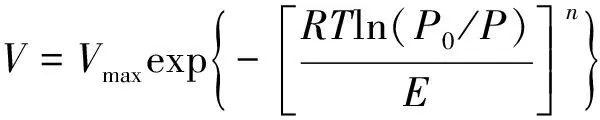
(1)

式中，为气体吸附量，mL/g；为饱和吸附量，mL/g；为理想气体常数，J/(mol·K)；为热力学温度，K；为平衡压力，MPa；为气体的饱和蒸气压，MPa；为特征吸附能；为吸附剂结构非均质性系数。

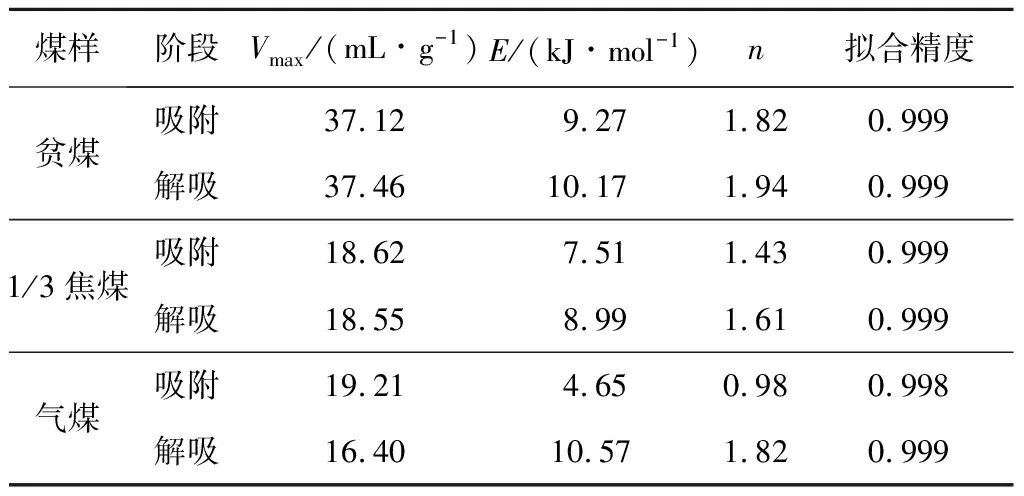
表2 D-A模型拟合参数

结合图3和表2可以发现，各煤阶原煤CO等温吸附/解吸特征存在以下规律：

(1)相同平衡压力条件下CO吸附量关系为贫煤>1/3焦煤>气煤，但饱和吸附量关系为贫煤>气煤>1/3焦煤。

(2)不同煤阶煤CO等温解吸曲线均位于等温吸附曲线上方，存在明显解吸滞后现象。采用IHI(Improved hysteresis index)吸附/解吸滞后定量评价模型(式(2))分析煤的解吸滞后性。

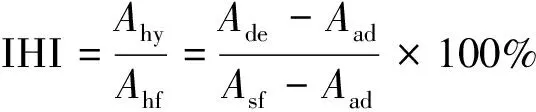
(2)

式中，为实测迟滞区域面积；为理想状态完全非可逆迟滞区域面积；为解吸曲线区域的面积；为吸附曲线区域的面积；为理想状态完全非可逆吸附区域面积。

IHI越接近1，解吸滞后性越强。根据式(2)计算得出贫煤解吸滞后系数是19%，1/3焦煤是28%，气煤是69%，显然，各煤阶煤样解吸滞后性关系为：气煤>1/3焦煤>贫煤。

2.2 等温吸附/解吸应变曲线变化规律

煤样等温吸附/解吸应变曲线如图4所示，图4中实线为等温吸附应变曲线，虚线为等温解吸应变曲线。体应变由纵向应变和横向应变数据计算得出。

从图4可以看出，气煤3吸附过程各向应变与平衡压力表现出线性关系(线性拟合精度>0.99)，其他煤样吸附/解吸过程各向应变与平衡压力均表现出非线性关系。相同平衡压力下，煤吸附/解吸体应变关系整体上表现为：贫煤>1/3焦煤>气煤，与相同平衡压力下CO吸附量关系一致，说明吸附量是影响煤吸附/解吸变形的主要因素。

从图4还可以看出，解吸过程中，不同煤样体应变曲线同时存在解吸应变滞后和解吸应变超前2种现象，并在完全解吸后存在残余变形和富余变形。其中，解吸应变超前现象指解吸体应变曲线位于吸附体应变曲线下方，相同平衡压力下解吸过程体应变小于吸附过程体应变；富余变形指完全解吸后煤样体应变为负值，煤样体积较原始体积缩小，解吸应变滞后和残余变形则相反。

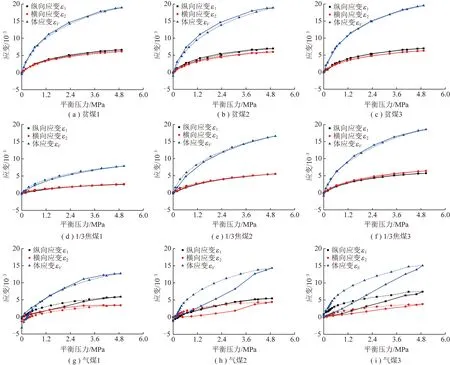
图4 煤样吸附/解吸过程应变-平衡压力关系曲线

此外，随煤阶升高，解吸体应变曲线逐渐由“滞后”转变为“超前”。气煤1整体表现为解吸应变超前，气煤2和气煤3则表现为明显的解吸应变滞后；1/3焦煤1和1/3焦煤2表现为解吸应变滞后，1/3焦煤3则表现为解吸应变超前，但滞后性和超前性都不明显；3个贫煤则均表现为解吸应变超前。文献[25]提出吸附态气体的解吸滞后性会导致解吸应变滞后特征。如前所述，气煤、1/3焦煤、贫煤3种煤样随煤阶升高，解吸滞后性逐渐减弱，促使煤的解吸体应变曲线由“滞后”向“超前”转变。

2.3 煤样变形各向异性特征

采用各向异性系数(不同平衡压力下煤样纵向应变与横向应变的比值)分析各煤样变形各向异性，计算结果见表3。

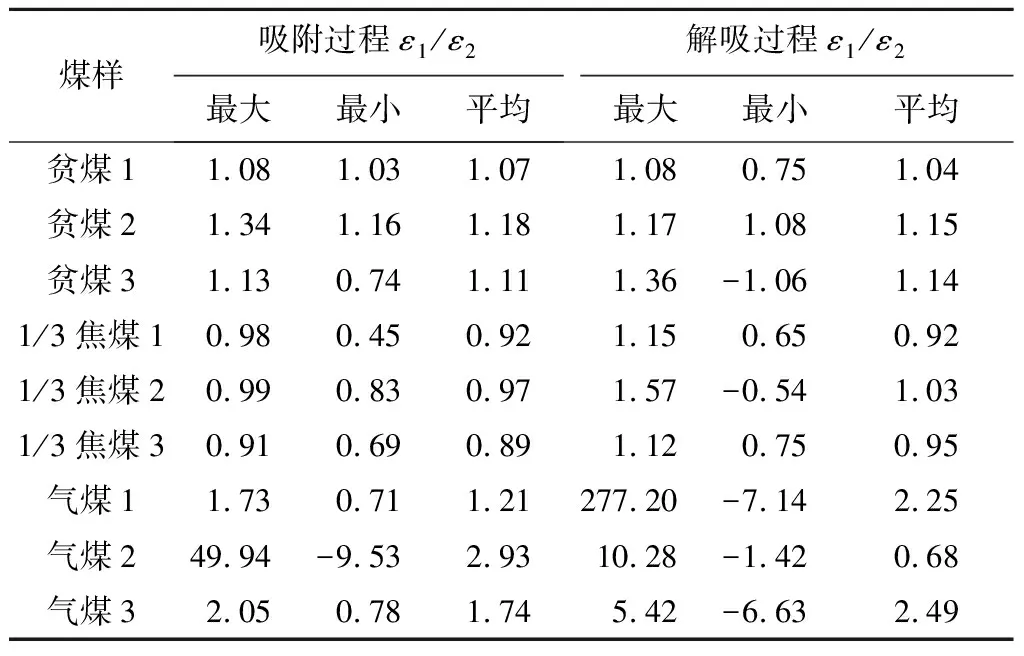
表3 煤样各向异性系数计算结果

表3中，各向异性系数为负值指煤样在平衡压力下纵向变形与横向变形方向相反，即一个表现为膨胀变形，另一个表现为收缩变形，多出现在低压解吸条件下。此外，为降低极端值对试验数据的影响，计算平均值时去除最小值和最大值。

由表3结合图4可知，多数情况下，原煤吸附/解吸的纵向应变大于横向应变(各向异性系数平均值>1)，但由于原煤具有非均质性，不同原煤煤样内部的孔裂隙结构存在差异，力学性质不尽相同，吸附/解吸过程中同样存在纵向应变与横向应变相差不大(各向异性系数平均值≈1，例如贫煤1解吸过程和1/3焦煤2的吸附/解吸过程)以及纵向应变小于横向应变(各向异性系数平均值<1，例如1/3焦煤1、1/3焦煤3的吸附/解吸过程以及气煤2解吸过程)的现象。

2.4 煤样变形离散性特征

由2.2节分析可知，吸附过程气煤各向应变与平衡压力同时存在线性和非线性关系，且气煤和1/3焦煤等温解吸应变曲线同时存在滞后性和超前性2种特征，原煤等温吸附/解吸应变曲线具有离散性特征。因此，采用变异系数(标准差/平均值)对吸附/解吸过程各平衡压力下体应变的离散程度进行分析，如图5所示。

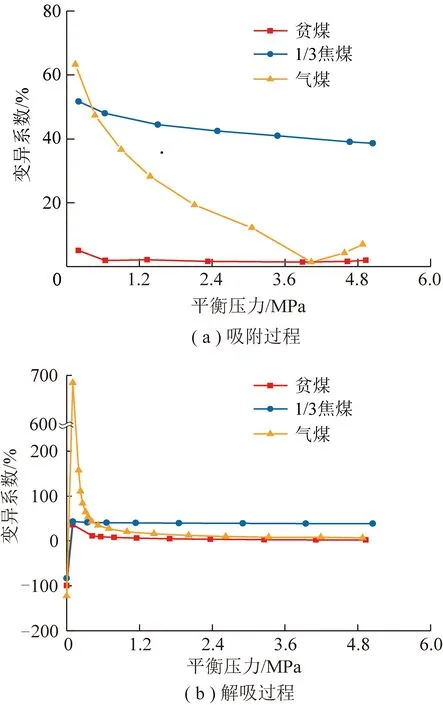
图5 煤样吸附/解吸变形离散性特征

由图5可以看出，吸附过程，贫煤各平衡压力下体应变量的变异系数介于1.42%～5.04%，平均值为1.86%；1/3焦煤介于38.61%～51.72%，平均值为42.99%；气煤则介于1.39%～63.29%，平均值为22.13%。解吸过程，贫煤各平衡压力下体应变量的变异系数介于-99.21%～35.85%，平均值为5.97%；1/3焦煤介于-83.07%～42.96%，平均值为39.96%；气煤则介于-122.53%～684.56%，平均值为43.75%(计算平均值时去除了最小值和最大值)。

由此可知，1/3焦煤和气煤吸附/解吸过程各平衡压力下应变量差异明显，离散性大；而贫煤各平衡压力下应变量无明显差异，离散性小。此外，从图5还可以发现，随平衡压力逐渐增大，吸附/解吸过程各煤样应变的变异系数逐渐减小，离散性降低。

3 煤体CO2等温吸附/解吸变形模型

3.1 体应变-吸附量关系模型

根据煤样等温吸附/解吸过程体应变和吸附量数据，得到体应变-吸附量关系如图6所示，图6中实线表示吸附过程，虚线表示解吸过程。

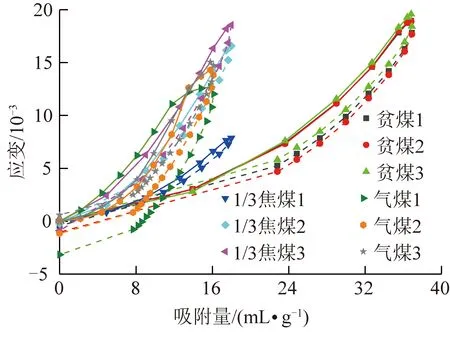
图6 煤样体应变-吸附量关系曲线

从图6可以发现，煤样吸附/解吸变形与吸附量具有明显的非线性关系，且气煤、1/3焦煤、贫煤3种煤阶煤样体应变-吸附量关系曲线随煤阶升高逐渐右移，表现为吸附相同量的CO，煤体产生的体应变逐渐减少，煤的膨胀变形能力(单位吸附量下产生的应变量，即应变量/吸附量)关系为气煤>1/3焦煤>贫煤。但从2.2节分析可知，相同平衡压力条件下不同煤阶煤吸附/解吸体应变关系为：贫煤>1/3焦煤>气煤，与各煤阶煤的膨胀变形能力关系相反。这是因为相同平衡压力下高煤阶煤CO吸附量更大，导致高煤阶煤即使膨胀变形能力较小，但相同平衡压力下仍具有更大的膨胀变形量。由此可知，煤样应变量由吸附量和膨胀变形能力综合决定。

煤样吸附/解吸过程中的膨胀变形能力曲线如图7所示。由于完全解吸后煤样存在富余变形或残余变形，即煤样解吸体应变-吸附量关系曲线存在截距，导致煤样膨胀变形能力的计算值为无穷大，但该截距对煤样解吸体应变-吸附量关系的整体规律没有影响。因此，将煤样完全解吸后的富余变形值或残余变形值作为常数项，通过上下平移解吸体应变-吸附量曲线消除截距，以煤样的富余变形值或残余变形值作为零点计算膨胀变形能力。

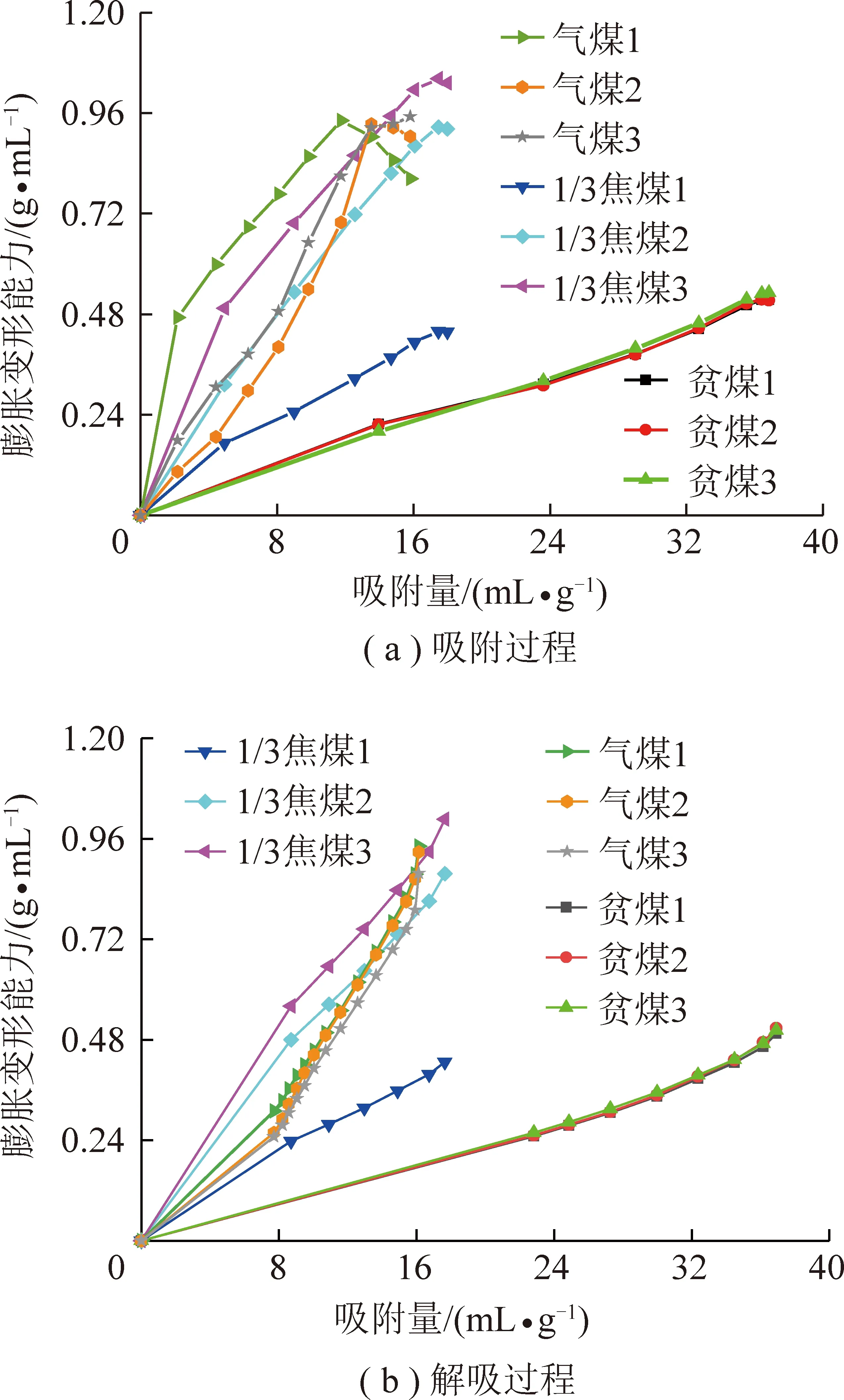
图7 吸附/解吸过程煤样膨胀变形能力曲线

由图7可以发现，吸附/解吸过程煤样的膨胀变形能力并非一个定值。采用线性函数、二次函数、幂函数等常用函数对各煤样吸附/解吸过程膨胀变形能力数据进行拟合，二次函数对吸附过程膨胀变形能力数据的拟合精度最高(除气煤1拟合精度为0.95，其余煤样拟合精度均>0.97)；二次函数和幂函数对解吸过程膨胀变形能力数据均具有较高的拟合精度(所有煤样的拟合精度均>0.99)，但考虑到解吸是吸附的逆过程，认为吸附/解吸过程煤样膨胀变形能力与吸附量的关系均可以用二次函数表示：

=+

(3)

=+

(4)

式中，为膨胀变形能力，g/mL；为吸附量，mL/g；为拟合参数，g/mL；为拟合参数，g/mL；下脚标x和j分别代表吸附过程和解吸过程。

进而得到吸附过程应变量与吸附量模型为

==+

(5)

式中，为吸附过程应变量，10。

由于完全解吸后煤样存在富余变形或残余变形现象，因此解吸过程应变量与吸附量模型应在现有模型基础上加上富余应变或残余应变量：

=+Δ=++Δ

(6)

式中，为解吸过程应变量，10；Δ为完全解吸后的残余应变量或富余应变量，10。

采用式(5)，(6)分别对吸附/解吸过程体应变-吸附量关系曲线的数据进行拟合，均具有较高拟合精度(所有煤样拟合精度均>0.98)，采用该模型能够较好反映体应变-吸附量关系，即煤样吸附/解吸CO过程中应变量和吸附量呈三次函数关系。

3.2 吸附/解吸CO2变形模型

煤体吸附/解吸变形是受吸附膨胀和孔隙压力影响的耦合过程。但现有理论模型普遍将吸附膨胀作用和孔隙压力作用导致的变形分开进行分析，忽略了2者之间的复杂耦合关系。一方面，气体吸附会诱发煤基质产生细观损伤，使煤的力学性质劣化，这将导致煤样受孔隙压力作用产生的变形更明显。另一方面，煤样在孔隙压力作用下发生变形也会改变煤样的孔裂隙结构，影响煤样的吸附量，进而影响煤体的吸附变形。而这些复杂耦合关系难以通过常规测试手段进行量化分析，只能通过煤样的应变量宏观反映。

因此，不宜分开讨论吸附膨胀作用和孔隙压力作用导致的变形，需要从整体角度着手，借鉴前人提出的“变形系数”的思想，采用吸附/解吸过程膨胀变形能力的变化反映吸附膨胀和孔隙压力对于煤样变形的综合作用。

基于此，考虑煤样应变量由吸附量和膨胀变形能力综合决定，将等温吸附模型(D-A方程)代入应变量-吸附量关系模型，即将式(1)代入式(5)和式(6)，建立样CO等温吸附/解吸变形模型如式(7)，(8)所示。

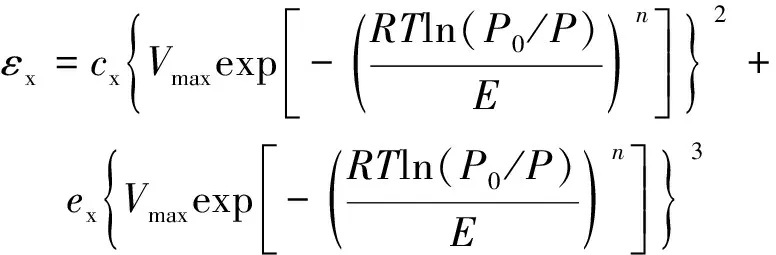
(7)

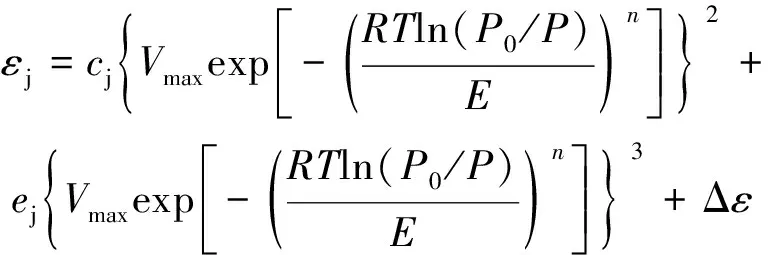
(8)

为验证本文所建模型的适用性和精确性，采用式(7)和式(8)对吸附、解吸过程煤的体应变数据进行拟合，并分别与Langmuir方程(式(9))以及改进的Langmuir方程(式(10))试验模型的拟合结果进行对比。结果见表4。

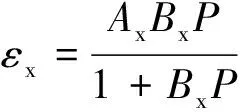
(9)

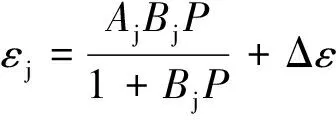
(10)

式中，为煤吸附气体后的极限应变量，10；为应变随气体压力发生变化快慢的参数，MPa。

从表4可知，Langmuir方程可以较好反映吸附过程煤样应变与平衡压力之间的非线性关系。但本文试验发现，吸附过程煤样应变与平衡压力同样存线性关系，明显不符合Langmuir方程规律，采用Langmuir方程描述煤的吸附变形特征具有一定的局限性。对比而言，式(7)对吸附过程各煤样应变数据则均具有较高的拟合精度(均>0.99)，适用性较广。

式(8)和改进的Langmuir方程均对解吸过程煤样应变数据具有较高的拟合精度(均>0.99)。但不论是Langmuir方程还是改进的Langmuir方程均是从试验现象角度描述煤样应变量与吸附平衡压力的关系，没有体现吸附量对煤样膨胀变形的作用。综上所述，笔者所建模型适用性较广，能够精确拟合煤吸附/解吸CO变形数据。

4 讨 论

针对煤吸附CO后发生膨胀变形，导致煤层渗透率降低的工程难题，实际生产中通常采用间歇式注入方法提高CO可注性。相对于持续注入，CO间歇式注入方式能够提升CO注入量，是目前生产中用的主要措施。牛庆合通过开展间歇注入CO的试验，提出在CO停注之后，其压力会逐步衰减。而从图4可以发现，压力降低会导致煤样发生收缩变形，进而使煤样因膨胀变形降低的渗透率得到一定程度的恢复，这是间歇式注入方式能够提高煤层CO可注性的重要原因。

综合分析气煤、1/3焦煤、贫煤3种煤样的吸附/解吸特征及变形特征，贫煤吸附能力最强，相同吸附量条件下膨胀变形能力最小，CO可注性最高。此外，贫煤等温解吸应变曲线表现出解吸应变超前现象，相同平衡压力下解吸过程体应变小于吸附过程体应变，煤样较吸附过程收缩，说明贫煤受气体压力降低的影响最大，更易发生解吸收缩变形，进而引起煤样渗透率的改善，更适用于间歇式注入提高煤层可注性技术。

气煤吸附能力较低，相同吸附量条件下膨胀变形能力大，会阻碍后续CO的注入，可注性较低。但其解吸滞后性最显著，其不易解吸的特点更利于CO的长期储存。此外，气煤等温解吸应变曲线存在显著的解吸应变滞后现象，相同平衡压力下解吸过程体应变大于吸附过程体应变，煤样较吸附过程膨胀，气煤受气体压力降低的影响较小，采用间歇式注入提高煤层可注性的效果不明显。

1/3焦煤相对其他2种煤样，不仅吸附能力较低，还具有较强的膨胀变形能力，可注性最差，解吸滞后性也明显低于气煤。针对该种煤样CO注入和封存的适用性还需结合现场实际进行深入考虑。

5 结 论

(1)3种不同变质程度煤均具有解吸滞后特征，且随煤阶升高，煤样解吸滞后特征减弱，促使煤解吸体应变曲线由“滞后”向“超前”转变。

(2)3种不同变质程度煤吸附/解吸变形均存在各向异性。气煤和1/3焦煤吸附/解吸变形离散性大，贫煤离散性小，3种煤样吸附/解吸变形的离散性均随着平衡压力增大而减小。

(3)相同吸附量条件下煤样吸附/解吸体应变关系为气煤>1/3焦煤>贫煤，但受吸附量影响，相同吸附平衡压力条件下煤样吸附/解吸体应变关系为贫煤>1/3焦煤>气煤，表明煤样应变量由吸附量和膨胀变形能力综合决定。

(4)吸附/解吸过程煤样的应变量和吸附量呈三次函数关系，结合煤的等温吸附模型(D-A方程)，建立了煤样吸附/解吸变形模型，能够精确拟合煤吸附/解吸CO变形数据，反映煤样吸附/解吸变形与吸附量及平衡压力关系。

(5)对比分析3种不同变质程度煤的吸附/解吸及变形特征，贫煤CO可注性最好，更适用于间歇式注入提高煤层可注性技术；气煤则更利于CO的长期储存。