输出误差约束下冷轧厚控系统的模糊反步控制

王建波，王芳，周超，华长春

(1. 燕山大学理学院，河北秦皇岛，066004；2. 河北农业大学海洋学院，河北秦皇岛，066003；3. 燕山大学电气工程学院，河北秦皇岛，066004)

在冷轧板带轧制过程中，板厚精度是板带质量的一个重要指标，因此，厚度控制是板带控制中的重要环节。在冷轧过程中，一方面，由于测量轧机出口厚度的传感器安置在离轧辊较远的位置，而轧机轧制速度是变化的，导致系统存在时变时延；另一方面，轧机在工作过程中会受到外界干扰，如轧辊偏心、咬钢或抛钢等，所以轧机是一个非线性不确定时滞系统[1-3]。上述因素给HAGC 系统控制器设计带来很大的困难，会导致系统控制精度降低甚至出现不稳定，而时延问题对系统的影响最大。

近年来，如何消除时延对控制系统的影响受到了学者们的广泛关注。华长春等[4]将系统转化为偏微分方程形式，并将未知时延参数化，设计出一种新型控制器。CHOU等[5]考虑状态时延系统的控制问题，设计了自适应变结构控制器。JAIN等[6]研究了具有未知输入时变时延的不确定Euler-Lagrange 系统的一致最终有界跟踪问题。OBUZ等[7]针对具有未知时变输入时滞和加性扰动的不确定非线性系统，设计了基于时延补偿的控制器。针对HAGC 系统时延影响下的控制问题，已有很多学者对其展开研究。方一鸣等[8]利用内模原理，设计极点配置自校正控制器。LIU等[9]利用李亚普诺夫-克拉索夫斯基(Lyapunov-Krasovskii)泛函稳定性理论，得出系统渐近稳定的充分条件，并设计了基于降维观测器的鲁棒输出镇定控制器。赵琳琳等[10]针对已知定常状态时延影响下的冷带轧机厚控系统，设计了自适应鲁棒输出反馈动态控制器。孙建亮等[11]建立了冷轧四辊轧机厚控模型，结合H∞混合灵敏度鲁棒控制理论和遗传算法，设计了H∞鲁棒控制器。HUA 等[12]考虑输入定常时延，设计了基于扩张状态观测器的预测控制器。LI 等[13]在状态变换中引入时延积分项，通过积分中值定理消除了HAGC 系统中的定常时延。以上研究主要考虑定常时延，但未考虑更适用于冷轧系统的时变时延。

为了保证HAGC 系统的输出误差满足要求，在设计控制器的过程中需解决输出误差约束问题，常用方法有预定性能控制和障碍Lyapunov函数法。BECHLIOULIS等[14]利用误差转换将输出误差性能约束问题转化为无约束问题。BECHLIOULIS等[15]结合误差转换方法，提出基于预定性能的鲁棒自适应控制方法。HUA 等[16]基于状态转换和性能函数，提出了输出反馈预定性能控制策略。WANG等[17]通过引入性能函数得到约束条件，设计了反馈控制器，使得最大超调量小于预先设定值。ZHANG等[18]针对具有输出约束的严反馈非线性系统，引入障碍函数，提出基于动态面的自适应控制器。陈强等[19]提出了基于时变障碍函数的自适应控制策略，该控制策略同时适用于系统有约束与无约束的情况，拓宽了障碍函数的适用范围。虽然有关非线性系统输出约束的理论研究较多，但有关冷轧厚控系统控制的研究较少。LI 等[13]结合反步控制和预定性能函数，设计了预定性能控制器，但是没有考虑时变时延的影响。

陈金山[20]对冷连轧机过程的建模以及控制问题进行了研究。此外，许多学者建立了HAGC 系统的线性数学模型并研究了该系统的控制问题[21-25]，但HAGC 系统本质上是一个非线性系统，且在建立其数学模型时，液压缸腔中背压、伺服阀中的非线性特性、轧辊间的摩擦和轧制力变化引起的弹性变形量这些都是未知的，故系统受到不确定因素的影响。HUA 等[12]结合HAGC 系统的实际情况，假设模型中的未知函数有界，并设计了预测控制器。LI 等[13]假设HAGC 模型中的未知非线性函数满足线性条件，并设计了预定性能状态反馈控制器。高玉峰等[26-33]针对参数不确定影响下的冷轧系统，设计了鲁棒解耦控制器。模糊逻辑系统能够以任意精度逼近非线性函数，模糊控制不需要假设未知非线性函数满足线性条件，可以较好地解决模型中的未知非线性函数问题。将模糊控制应用于冷轧厚控系统，有助于提高板带的精度。TONG等[34]利用模糊逻辑系统逼近未知的非线性项。王慧等[35]利用模糊推理方法，实现了对PID参数的在线自动修改适应，并设计了模糊自整定PID控制器。

目前，人们针对HAGC 系统的控制方法进行了大量研究。李讯等[36]设计了解耦控制，提高了板厚板形精度。宋东球等[37]结合Smith预估控制器对厚度系统进行补偿。高玉峰等[38]针对模型参数不确定的冷轧系统，设计了多变量鲁棒解耦控制器。孙文权等[39]建立了高精度冷轧自动控制系统，并证明平坦度与板厚解耦设计可有效提高板形板厚的控制精度。樊立萍等[40]将PID控制与模糊控制结合，克服了传统PID 控制调整周期长的问题。SHI等[41]提出了输出概率约束最优控制算法，将输出概率约束转化为确定性约束。以上关于HAGC系统控制的研究取得了较好的控制效果，但是多基于线性系统。另外，冷轧系统的测量时延是时变的，且系统受不确定因素的影响。

基于以上分析，本文针对时变时延、输出误差约束和外界干扰影响下HAGC系统的控制问题，设计基于障碍Lyapunov函数的模糊反步控制策略。首先，将系统的测量时变时延转化为输入时延，并构造辅助系统补偿输入时延对系统的影响；其次，利用干扰观测器处理系统中的综合不确定问题；采用障碍函数解决输出误差约束问题；通过Lyapunov 稳定性理论，证明闭环系统有界稳定。最后，通过对比仿真验证本文所提出控制策略的有效性。

1 冷带轧机液压厚度系统模型

冷带轧机液压厚度系统主要是由液压缸、电液伺服阀、传感器、轧机辊系、供油管、背压回油管等动态元件组成，其结构示意图如图1所示。

根据图1，由冷带轧机液压厚控系统中各部件的运行机理可得如下动力学模型[3]：

式中：xp，PL和hout分别为油缸活塞位移、负载压力和考虑了测量时延τ(t)的轧件出口厚度；t为时间；τ为测量时延；Mt为轧机辊系运动部件等的有效质量；Kt为负载弹性刚度系数；Bp为运动部件的黏性系数；W为轧件塑性刚度系数；Ap为液压缸活塞有效面积；Vt为液压缸油腔总体积；βe为体积弹性模量；C为液压缸泄漏系数；Kc为伺服流量放大系数；Kp为伺服放大器比例系数；Kv为阀芯位移放大系数；Kq为流量放大系数；Th为惯性时间常数；Ksv=KqKvKp；xv为阀芯位移；i为电流；δ1(xp,，δ2(xp,和δ3(xp,L)分别为系统中由伺服阀中的非线性特性、轧辊偏心以及轧辊系的摩擦力引起的未知的非线性项。

选取状态变量x1=hout-houtd，x2=xp-xpd，x3=4=PL-PLd，其中houtd，xpd和PLd分别为轧件出口厚度、缸位移和负载压力的期望值。由于咬钢、抛钢以及轧辊偏心都会引起外部扰动的产生，故有必要考虑HAGC 系统的外部扰动，结合系统动力学模型[3]，将测量时延转化为输入时延[4]，则式(1)可转化为

式中：y1为系统的输出；u(t-τ(t))为带有时延的输入；X=[x1,x2,x3,x4]T，为系统的状态列向量；d1，d2和d3为外界干扰；τ(t)为系统时延；δ1(X)，δ2(X)和δ3(X)为非线性函数，

本文利用模糊逻辑系统逼近式(2)中的未知非线性项。模糊逻辑系统包含模糊推理机制、模糊规则、模糊化和去模糊化4个部分。模糊推理基于IF-THEN形式模糊规则，其第j条规则如下：

其中，y为模糊集的输出；和为模糊集；和μBj(y)均为模糊系统的隶属函数；模糊规则数为M，采用乘积推理、中心平均解模糊器和单值函数，得到模糊逻辑系统的输出y(X)：

其中，为μBj(y)的最大值；Sj(X)为模糊逻辑系统的基函数。

引理1[34]：f(X)是定义在紧集Ω上的函数，∀ε＞0，存在一个模糊逻辑系统，使得下式成立：

其中，W为模糊系统的理想权重向量；S(X)为模糊基函数向量；ε为逼近误差，满足|ε|≤，为正常数。

引理2[42]：若|z|＜kb，kb为任意正数，则有：

注释1本文基于障碍Lyapunov 函数对系统输出误差进行约束，使输出误差z1=x1-x1d满足如下约束条件：

其中：x1d为x1的参考指令；kb1为正常数，表示HAGC系统中输出误差的约束界限值。

定义1[43]：障碍Lyapunov 函数是一个标量函数，是在包含原点的开区域D上相对于系统=f(x)定义的，即它是正定的、连续的且在D的每个点具有连续一阶偏导数，当接近D的边界时，有V(x)→∞，并且由x(0)∈D所对应的=f(x)的解和一个正常数b可得，对于∀t≥0，有V(x(t))≤b成立。

假设1：外界干扰di(i= 1,2,3)及其导数满足其中和为正常数。

假设2：时变时延τ(t)满足τ(t)≤其中τ0，为时延上界。

假设3：输出参考指令x1d与有界。

控制目标：针对具有输入时延和外界干扰的冷轧厚控系统(式(2))，设计基于障碍函数的自适应反步控制策略，使系统达到半全局一致有界稳定，且系统输出误差满足约束要求|z1|＜kb1。

2 控制器设计

本节基于式(2)，设计自适应反步控制策略。引入障碍函数对系统输出误差进行约束，设计时延辅助系统补偿输入时延，并利用干扰观测器估计综合不确定项，利用模糊逻辑系统理论逼近未知非线性函数，进而在反步控制的框架下设计控制器，具体过程如下。

为了解决HAGC 系统的时变时延问题，参考文献[44]，设计如下辅助系统：

式中：λ1，λ2和λ3为辅助系统的状态变量；b1，b2，b3为大于0的常数。

基于辅助系统(式(3))，进行如下状态变换：

式中：α1，α2和α3为虚拟控制输入。

下面基于式(2)～(4)设计控制器。

1)步骤1：设计虚拟控制输入α1。

对z1求导，则由式(2)可得：

式中：f1=δ1(X)，为未知非线性函数，利用模糊系统逼近，则f1=W1TS1(X)+ε1；ε1为逼近误差，且|ε1|≤；为正常数。令D1(D1=d1+ε1)为综合不确定项，则式(5)可表示为

通过干扰观测器估计综合不确定项D1：

式中：ξ1，ς1和φ1为干扰观测器的辅助变量；为D1的估计，估计误差

选取如下障碍Lyapunov函数：

注释2本文结合定义1 选取式(8)中的障碍Lyapunov 函数对输出误差进行约束，由于函数中的kb1是常数，故这种形式的障碍Lyapunov 函数只能解决输出误差约束形式是对称的且输出误差约束界限值是常值的情形。

设计如下虚拟控制输入α1：

的自适应律为

式中：σ1为正常数。

由式(9)～(11)可得：

2)步骤2：设计虚拟控制输入α2。

对z2求导，则由式(2)可得:

式中：f2=为未知非线性函数，利用模糊系统逼近f2，则f2=W2TS2(X)+ε2；ε2为逼近误差。|ε2|≤；为大于0的常数。

选取Lyapunov函数V2：

注释3HAGC系统是实际工程系统，借鉴电学和力学分析中能量函数的表达式，选取为系统的误差信号)形式的Lyapunov函数，分析闭环系统的稳定性。

结合式(13)和(14)可得：

设计如下虚拟控制输入α2：

其中的自适应律为

式中：σ2为正常数。

将式(16)和(17)代入式(15)得：

式中：k2o=k2-为正常数。

3)步骤3：设计虚拟控制输入α3。

对z3求导，则由(2)可得:

式中：f3=δ2(X)-为未知非线性函数，利用模糊系统逼近f3，则f3=W3TS3(X)+ε3；ε3为逼近误差。|ε3|≤为大于0 的常数。令D2为综合不确定项，D2=d2+ε3，则式(19)可表示为

通过干扰观测器估计综合不确定项D2：

式中：ξ2，ς2和φ2为干扰观测器的辅助变量；为D2的估计，估计误差

选取以下Lyapunov函数：

结合式(20)和(21)可得：

设计如下虚拟控制输入α3：

其中的自适应律为：

式中：σ3为正常数。

由式(23)～(25)可得：

4)步骤4：设计控制输入u。

通过干扰观测器估计综合不确定项D3：

由式(28)～(30)可得：

设计控制输入u：

其中的自适应律为

式中：σ4为正常数。

将式(32)～(33)代入式(31)可得：

本文基于HAGC 系统设计模糊反步控制器，其结构示意图如图2所示。

注释4李迅等[45]利用Smith估计器消除了AGC系统中的时延影响。HUA等[12]提出Smith预估控制策略以消除HAGC 系统输入定常时延的影响。顾波等[46]提出了改进型Smith算法，解决了监控AGC系统时的时延问题。

本文设计辅助系统补偿HAGC 系统中输入时变时延对系统的影响，该方法同样适用于输入定常时延。

注释5王丽君等[47]通过扩张状态观测器实现了对AGC系统的总扰动(包括内部不确定性和外部扰动)的实时估计。华长春等[4,9,12]在建立HAGC系统模型时，将伺服阀中的非线性特性、轧辊偏心、轧辊间的摩擦力等因素描述为一个未知的非线性函数，利用神经网络逼近未知的非线性函数，但未考虑系统在运行过程中受到的外界干扰的影响。本文同时考虑外界干扰和未知非线性项，利用模糊逻辑系统逼近未知的非线性函数，通过干扰观测器估计综合不确定项。

3 稳定性分析

下面基于Lyapunov 稳定性理论分析闭环系统的稳定性。

定理1冷轧厚控系统(式(2))满足假设1，2 和3，不考虑时延影响，系统在干扰观测器(式(7)，(21)和(29))、模糊自适应律(式(11)，(17)，(25)和(33))以及控制器(式(32))作用下，系统变量zi，和有界。

证明：选取Lyapunov函数V，

式(35)关于时间的导数为

根据式(12)，(18)，(26)，(34)可知，式(36)满足：

式中：

对式(37)两端同乘eϖ1t并积分得：

时延补偿系统的稳定性分析可总结为以下定理。

定理2时延补偿系统(式(3))满足假设2，则在虚拟控制器(式(10)，(16)，(24))和控制器(式(32))的作用下，λi有界。

证明：选取Lyapunov-Krasovskii泛函数Vλ，

式中：μ1和μ2为正常数；s为积分变量。

根据的分析过程可得：

由柯西史瓦兹不等式可得：

结合式(41)，则有：

通 过 式(10)，(11)，(16)，(17)，(24)，(25)，(32)和(33)，分别可得u(t)和的表达式为：

将式(45)和式(46)代入式(42)得：

构造如下Lyapunov函数：

式中：υ为大于0的常数。

由式(47)～(48)得：

由柯西史瓦兹不等式可得：

根据式(49)～(51)，则有：

对式(52)两端同乘eϖ2t并积分得：

闭环系统的稳定性可以总结为如下定理。

定理3冷轧厚控系统(式(2))满足假设1，2 和3，则在干扰观测器(式(7)，(21)和(29))、模糊自适应律(式(11)，(17)，(25)和(33))以及控制器(式(32))作用下，系统半全局一致有界稳定，且输出误差满足预先设定的约束条件。

证明：选取Lyapunov函数Vo为

结合式(34)和(52)，可得：

式中：C3=C1+C2，ϖ= min {ϖ1,ϖ2}。

对式(55)两端同乘eϖt积分得：

结合式(8)和(56)可知输出误差满足：

由式(57)可知，输出误差z1在区间(-kb1,kb1)内，系统输出误差满足预先设定的约束条件。定理3证明完毕。

通过以上分析可知，系统在基于障碍函数的自适应控制器的作用下达到半全局一致有界稳定，且输出误差满足预设的约束条件。

注释6LI 等[13]通过设计预定性能控制器对系统输出进行约束，但计算和求导过程较复杂，而本文采用的障碍Lyapunov 函数保证了系统输出约束，且减少了计算量，使得控制器设计过程变得相对简单。

4 仿真分析

为验证本文所提控制策略的有效性，基于冷轧HAGC厚控模型(式(2))进行仿真分析，本文选取1700单机架轧机进行仿真验证。

轧机的规格参数如下：支持辊直径×长度为1 371 mm×1 700 mm，工作辊直径×长度为914 mm×1 700 mm。液压系统参数如下：缸径为720 mm，杆径为600 mm，行程为40 mm。仿真分析中系统的主要参数取值见表1。

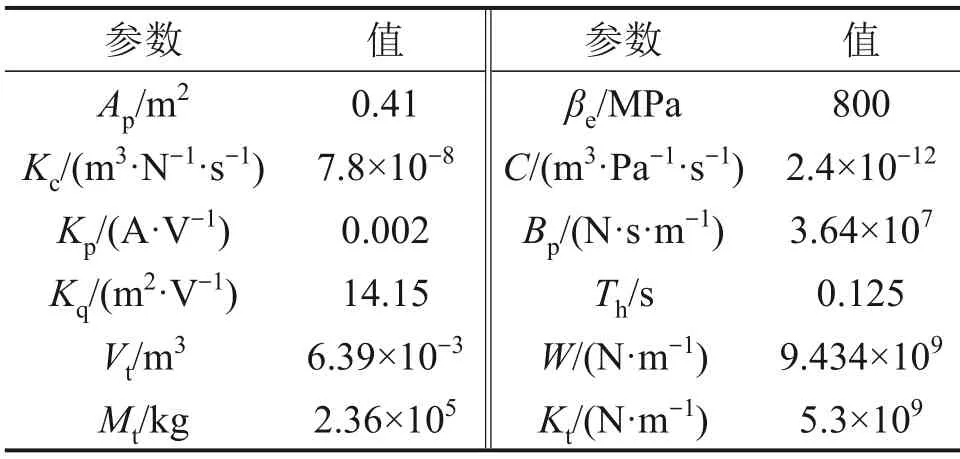
表1 HAGC系统主要参数取值Table 1 Main parameters and its values of HAGC system

由于HAGC 系统中的干扰主要是由轧辊的工作引起的，由文献[48]可知轧辊的偏心现象可以用三角函数Asin(ωt+φ)表示，其中A为辊偏心信号振幅，ω为辊偏心信号角速度，φ为辊偏心信号起始角。本文考虑支持辊、工作辊和整个辊系的偏心，结合文献[13]选取如下干扰形式：d1=0.000 1sin(17.4t+ π/4)，d2= 0.2 sin(0.2t)，d3=0.25 sin(31.75t+ π/2)。

注释7HAGC系统中的干扰主要是由轧辊偏心引起的，但干扰还有轧辊磨损、间隙和油膜厚度变化等因素，这些因素可以表示为一个未知项，而HAGC 系统的数学模型中也含有未知项，故在设计控制系统时将这2 个未知项合并为1 个未知项，而在研究干扰对系统的影响时，主要研究轧辊偏心对系统的影响。

出口侧轧制中心线到测厚仪之间的距离L和出口侧带材速度w1是造成测量时延的原因，且τ=L/w1，而实际系统中速度w1是变化的，且受到外界干扰和摩擦等因素的影响，故选取时延τ(t)=0.6+0.1sin(t)进行仿真验证。初始值为：X=[0.0010，-0.000 1，0.002 0，-1.000 0]；出口厚度期望值为x1d=0.000 1e-5t。 控制器参数如下：b1=50，b2=15，b3=50，b4=1，k1=15，k2=30，k3=50，k4=10-14，σ1=50，σ2=80，σ3=150。本文期望的板带材宽度为1 300 mm，厚度为1 mm，根据国家标准GB/T708—2019“冷轧钢板和钢带的尺寸、外形、重量及允许偏差”规定，在较高精度标准下，钢板最小屈服强度小于260 MPa，宽度为1 200～1 500 mm，厚度为0.80～1.00 mm，轧件允许的厚度偏差为±0.04 mm。但现代板带轧机大型工业生产线HAGC 系统通过组合应用各类厚度控制技术，可将纵向厚度偏差稳定地控制在±5 μm甚或±2 μm 范围内。故本文选取输出误差约束如下：≤5.3 μm。为了验证控制器的有效性，在考虑输出误差约束与外界干扰、不考虑外界干扰和不考虑输出误差约束3 种条件下进行仿真对比，结果分别如图3～8所示。

图3所示为轧件厚度误差x1对期望厚度误差x1d的跟踪效果。由图3可知3种情况下的轧件厚度误差大约在0.8 s 实现了对期望厚度误差x1d的跟踪。图4 所示为输出误差z1的响应图。由图4 可见输出误差大约在0.8 s 达到稳定，且考虑输出约束和不考虑干扰条件下的输出误差始终在约束区域内；而不考虑输出约束情形下的输出误差超出了预先设定的约束界限值。由图5～7 可知，缸位移误差x2、缸速度误差x3和负载压力误差x4大约在0.2 s达到了稳定。图8所示为控制输入u的响应曲线。由图8可知，控制输入曲线光滑无抖振。

综合以上分析可知，考虑输出误差约束时，输出误差一直保持在约束范围内，而不考虑输出误差约束时，输出误差超出约束范围。由图5～7可知，3种情形下的缸位移误差x2，缸速度误差x3和负载压力误差x4的曲线在0.2 s 附近都趋于稳定，但不考虑约束条件下的稳态误差大于考虑约束条件下的稳态误差，所以考虑输出误差约束时的控制效果优于不考虑输出误差约束时的控制效果。

5 结论

1)针对存在时变时延、输出误差约束和外部扰动的HAGC系统，提出模糊反步控制策略。

2)设计辅助系统补偿时延对系统的影响，利用障碍Lyapunov 函数，保证了输出误差在预设区间内。

3)采用模糊逻辑系统理论逼近未知的非线性函数，通过干扰观测器估计了综合不确定项。

4)仿真对比结果表明，所提出的控制策略实现了输出的稳定跟踪，系统输出误差保持在约束范围内，且其瞬态和稳态性能优于不考虑输出误差约束时的瞬态和稳态性能。