巧用凹凸性 妙解数学题
江苏 戚有建
函数的凹凸性是高等数学中的一个重要的数学概念,虽然在高中数学教材中没有明确出现凹凸性这个概念,但是在高考题中却经常可以看到凹凸性的踪影,实际上凹凸性是高等数学和初等数学的一个衔接点,在研究函数的凹凸性时,可以用导数作为工具,这样就将凹凸性与高中数学中的导数知识联系起来.凹凸性在研究函数最值、证明不等式等方面有着广泛的应用,近年来,以凹凸性为背景的试题已多次出现在高考中.笔者认为,在进行函数性质的教学时,教师可以适当补充一下函数凹凸性的相关内容,这样能够帮助学生全面深刻地理解函数的概念和性质.本文以几道高考题为例,剖析其中的凹凸性踪影,以期抛砖引玉.
1.凹凸性的定义
设函数f(x)是在区间I内的函数,若对任意x1,x2∈I(x1≠x2),


2.凹凸性的几何特征
(1)形状特征
凹函数(或下凸函数)的形状特征:曲线任意两点A1与A2之间的部分位于弦A1A2的下方;
凸函数(或上凸函数)的形状特征:曲线任意两点A1与A2之间的部分位于弦A1A2的上方.
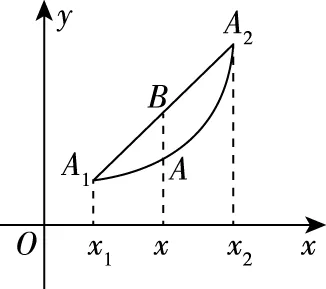
(凹函数)

(凸函数)
(2)切线斜率特征
凹函数(或下凸函数):切线的斜率随x增大而增大;
凸函数(或上凸函数):切线的斜率随x增大而减小.
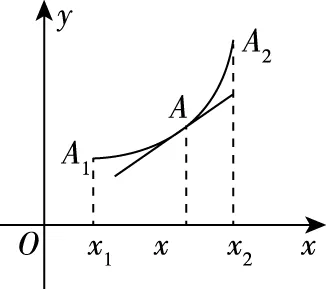
(凹函数)

(凸函数)
3.凹凸性的推广:琴生不等式


4.凹凸性的判断
设函数f(x)在区间I上二阶可导,
(1)若对任意x∈I,都有f″(x)>0,则f(x)在区间I上为凹函数(或下凸函数).
(2)若对任意x∈I,都有f″(x)<0,则f(x)在区间I上为凸函数(或上凸函数).
5.凹凸性的应用
由于凹凸性与导数密切联系,而导数是高考考查的重点、热点和难点,这就为高考命题提供更多的素材和视角.借助凹凸性,可以解决很多最值问题和不等式问题.
【例1】已知函数f(x)=(1-x2)ex,当x≥0时,f(x)≤ax+1恒成立,求a的取值范围.

解析:由题意得∀x∈[0,+∞),不等式(1-x2)ex≤ax+1恒成立.
方法1:研究差函数g(x)=(1-x2)ex-ax-1的最值
令g(x)=(1-x2)ex-ax-1,x∈[0,+∞),则g′(x)=(1-2x-x2)ex-a,故g″(x)=-(x2+4x+1)ex<0,
所以g′(x)在[0,+∞)上单调递减,而g′(0)=1-a,所以可得:
①当a≥1时,g′(x)≤g′(0)=1-a≤0,所以g(x)在[0,+∞)上单调递减,所以g(x)≤g(0)=0,符合要求;
②当0≤a<1时,g′(0)=1-a>0,g′(1)=-2e-a<0,又g′(x)在[0,+∞)上单调递减,
所以由零点存在性定理得∃x0∈(0,1),使得g′(x0)=0,当x∈(0,x0)时,g′(x)>0,所以g(x)在(0,x0)上单调递增,所以g(x)>g(0)=0,不符合要求;

综上,a的取值范围是[1,+∞).
点评:方法1是处理含参不等式恒成立问题常用的方法,也就是将不等式恒成立问题转化为求差函数最值问题,然后研究不等式“g(x)max≤0”,此种解法通俗易懂,学生容易想到.但由于本小题中引入了参数a,故需要对参数a分情况讨论处理,这对学生的思维能力提出了较高要求,另外其中0≤a<1的情形中还会遇到“g′(x)=(1-2x-x2)·ex-a,x∈[0,+∞)的零点不方便求出”的困难,这里需要“设而不求”来处理,这对学生来说有一定难度.
方法2:借助凹凸性,研究不等式
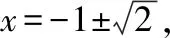
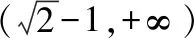
因为当x≥0时,f″(x)=-(1+4x+x2)ex<0,所以f(x)在[0,+∞)上是上凸函数,

函数y=f(x),y=ax+1都过(0,1),要使得当x≥0时都有f(x)≤ax+1,则需直线y=ax+1的斜率大于等于f(x)在(0,1)处的斜率,即a≥f′(0)=1.
点评:方法2是借助函数的凹凸性研究参数的取值范围.在高考中,可以借助一阶导数研究函数的单调性,画出函数的大致图象,再借助二阶导数来研究函数的凹凸性,这样就给我们处理切线的斜率问题、不等式恒成立问题提供了新视角、新方法.

(1)求a,b;(2)证明:f(x)>1.
解析:(1)a=1,b=2(过程略);

方法1:借助重要不等式证明函数不等式
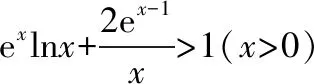
先证ex≥ex,x∈R设d(x)=ex-ex,则d′(x)=ex-e,令d′(x)=0,则x=1,
当x∈(-∞,1)时d′(x)<0,,故d(x)在(-∞,1)上单调递减;
当x∈(1,+∞)时,d′(x)>0,故d(x)在(1,+∞)上单调递增,
所以d(x)min=d(1)=0,故d(x)≥0,即ex≥ex,x∈R(当且仅当x=1时取等号).
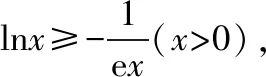


方法2:构建两个函数,借助凹凸性处理
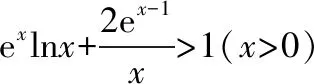




故g(x)在(0,1)上单调递增;在(1,+∞)上单调递减;
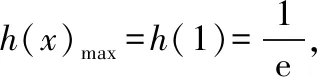
点评:方法2构建了两个函数g(x),h(x),加强为证明g(x)min>h(x)max,这里需要特别指出的是,g(x)min>h(x)max实际上是g(x)>h(x)的充分条件,而非充要条件.因为函数y=g(x),y=h(x)的凹凸性不同,其中y=g(x)是下凸函数,y=h(x)是上凸函数,所以也称为凹凸反转法,凹凸反转的关键是如何分离函数,分离的要求是什么呢?通常是指、对分离,即将指数函数与多项式函数的组合放在一边,将对数函数与多项式函数的组合放在一边.






6.反思感悟
首先,高考是选拔性考试,命题专家喜欢在初等数学和高等数学的交汇点处命题,这样设计的试题,立意高远、角度新颖,既能考查学生当前的数学素养,又能考查学生将来的学习潜能,既能实现高考的选拔功能,又能对中学教学起到良好的导向作用,而凹凸性就是这样的一个典型素材.



