一题多解引领深度学习——一道多变量最值问题的7种解法

唐 健

(金华第一中学,浙江 金华 321015)

1 问题呈现

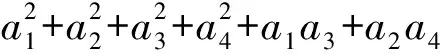
2 解法探究

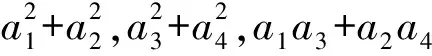
因为a1a4-a2a3=1，所以

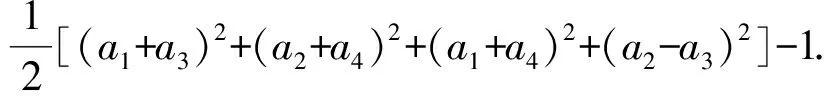
设A(a1,a2),B(-a3,-a4),C(-a4,a3),则上式具有几何意义：

(a1+a3)2+(a2+a4)2=|AB|2,

(a1+a4)2+(a2-a3)2=|AC|2,

显然OB⊥OC,且|OB|=|OC|,记|OB|=|OC|=d，因为a1a4-a2a3=1，所以

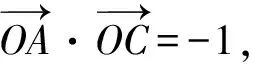
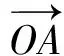
图1

图1

|AB|2+|AC|2=|BE|2+|EA|2+|AD|2+|CD|2

等号条件显然成立.

评注该解法的关键在于根据条件与所求的代数结构，联想出相关的等式，发现等式中各代数式的几何意义，体现了数形结合思想.在最后的计算中使用了两次基本不等式，需要注意两个等号要同时成立.

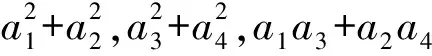
(a1a3+a2a4)2+(a1a4-a2a3)2

由a1a4-a2a3=1,得

即

当a1a3+a2a4=t时,

由单调性可知最小值为2.

当a1a3+a2a4=-t时,

评注该解法的思路与解法1相同，不过得到了不同的等式，通过换元，结合基本不等式实现消元，最终简化成函数求最值的问题.

解法3在解法2中得到

观察结构特征，构造向量a=(a1,a2),b=(a3,a4).设a,b的夹角为θ，由a1a4-a2a3=1，知a,b不共线,从而0<θ<π,上式转化为

(a·b)2+1=|a|2·|b|2,

即

|a|2·|b|2cos2θ+1=|a|2·|b|2，

得

=|a|2+|b|2+a·b

≥2|a|·|b|+|a|·|b|cosθ

评注该解法是在解法2中得到等式后，观察到等式中代数结构的几何意义，引入向量，通过代入消元和基本不等式转化成三角函数最值问题.

解法4设a3=x，a4=y,则

a1y-a2x=1，

表示一个圆.

从而

即

评注题中有4个变量，通过设置变量主次，把问题转化成直线与圆的位置关系问题，使问题瞬间简化，非常巧妙，给人豁然开朗的感觉.

解法5设a=(a1,a2),b=(a3,a4),则

|a×b|=|a|·|b|sinθ=|a1a4-a2a3|=1,

得

=|a|2+|b|2+a·b

≥2|a|·|b|+|a|·|b|cosθ，

下同解法3(略).

评注该解法应用了向量叉乘运算，找到变量间关系后，通过代入消元和基本不等式转化成三角函数最值问题.若学生已掌握相关运算，则难度就会下降很多.

解法6设a1=r1cosα，a2=r1sinα，a3=r2cosβ，a4=r2sinβ，则

a1a4-a2a3=r1r2cosαsinβ-r1r2sinαcosβ

=r1r2sin(β-α)=1,

即

又a1a3+a2a4=r1r2cosαcosβ+r1r2sinαsinβ

=r1r2cos(β-α),

下同解法3(略).

评注该解法应用了两次三角换元，转换已知条件，简化所求的结构，通过代入消元和基本不等式转化成三角函数最值问题.

解法7根据复数运算

(a1+a2i)(a4+a3i)=(a1a4-a2a3)+(a1a3+a2a4)i,

记a1+a2i=z1，a4+a3i=z2，a1a3+a2a4=B，则

z1z2=1+Bi，

从而

=|z1|2+|z2|2+B≥2|z1|·|z2|+B=2|z1z2|+B

下同解法3(略).

评注该解法引入了复数，对学生的代数转化能力和复数运算能力要求较高.

3 解后反思

以上7种解法各有所长，用到了不同的知识，大大拓宽了学生的视野.在课堂上，学生表现出了浓厚的兴趣，惊叹之余，也都收获颇丰.进行一题多解和多题一解的训练，有助于拓宽学生的思维，将数学学习引向深处[1].

此外，总结与反思是数学解题学习最重要的环节之一.问题解决之后，首先要检查和验证，确保无误，比如避免漏解、错解等情况.当解题过程冗长而复杂时，还应试着去改进，除去不必要的步骤[2].其次，总结解题方法.解题时使用了哪些基本方法,还有没有其他的方法,不同解法的优劣如何？第三，总结推广.思考本题运用了哪些知识，涉及哪些基本方法，它主要适用于何种问题，能否把结论或方法用于其他问题，题目是否可进行变式推广，与其他问题有什么关联，等等.