操作中找联系,梳理中悟本质
摘 要:《立体图形的表面积和体积(复习)》是六年级的一节总复习课。复习课既要巩固学生已学的知识与方法,又要优化他们的认知结构,帮助他们感悟数学思想方法。因此,复习立体图形时要基于联系的观点,在图形的运动和变化中探索面与体的关系,帮助学生全面、系统地理解与掌握立体图形表面积和体积计算方法。
关键词:《立体图形的表面积和体积(复习)》;自主梳理;认知结构
【教学内容】
苏教版小学数学六年级下册第94—95页。
【课前思考】
苏教版教材对“立体图形”的编排有层次、有梯度:学生在第一学段初步认识实际物体和几何图形,在第二学段了解立体图形的特征,学习立体图形表面积和体积的计算方法,并初步探究图形间的关系。但在实际教学中,存在“就题论题、蜻蜓点水”的现象,导致学生缺少多途径循证、多元化表征的机会,无法建立起知识之间的联系,对立体图形知识点的理解呈散点化、单一化,对表面积和体积计算方法的运用较为形式化。因此,复习课要基于联系的观点,通过引导学生梳理立体图形的特征、立体图形表面积和体积计算公式等,渗透线、面、体之间的联系,帮助学生全面、系统地理解与掌握立体图形的核心知识,搭建立体图形知识框架。
【教学目标】
1.在观察、操作、想象、交流等活动中,丰富对立体图形的认识,理清它们之间的联系和区别,体验三维立体图形与二维平面图形之间的相互转化,发展空间观念和极限思想。
2.在自主探索、合作交流等过程中系统地复习立体图形知识,积累研究问题的经验,增强学好数学的信心,渗透事物是相互联系、发展变化的辩证思想。
【教学过程】
一、自主梳理,引发思考
课前学生完成“研究学习单”(如下页图1)。
二、交流展示,理清脉络
(一)小组交流,回顾整理
师:同学们,今天这节课,我们来复习立体图形的表面积和体积。课前,大家已经通过“研究学习单”进行了回顾和整理,下面请同学们根据活动要求,在小组内交流。
出示活动要求:(1)组员有序交流,介绍立体图形的特征、立体图形表面积和体积的计算方法,并做好补充或完善,准备全班汇报;(2)在整理与反思的过程中,会产生一些新的发现或疑问,与小组成员进行探讨,并尝试解决。
(二)全班交流,梳理整合
师:我们学习的这些立体图形,它们都有什么特征?它们之间又有哪些联系和区别?
师:你们会计算这些立体图形的表面积和体积吗?怎么算呢?
师:长方体、正方体和圆柱的表面积计算方法虽然不同,但它们之间有什么相似的地方呢?结合展开图想一想,和同桌说一说你的发现。
师:长方体的体积公式是怎样推导出来的呢?你能画图向全班同学解释一下吗?圆柱的体积公式又是怎样推导出来的?计算圆锥体积时为什么要乘三分之一?
[设计意图:复习不是对单个知识点的重复教学,而是对学生已有学习方法和知识的精准概括和结构化整理,需关注学生对复习内容的深层次理解。因此,笔者设计了指向“探索图形之间联系”的活动,先通过列举立体图形的表面积公式,帮助学生将脑海中的知识有序提取出来;再在交流、对比、补充的过程中,帮助学生明晰表面积计算方法的相通之处,形成结构化的数学思维;最后,让学生回忆、整理立体图形的体积公式,将点状的知识串联成线,构建立体图形的体积计算方法体系。]
三、操作想象,沟通面与体的联系
(一)研究立体图形的表面积
师:上课前,我们思考了“一张长方形纸可以‘做出哪些立体图形”,接下来,我们交流一下。
预设1:“卷”的方法。
师:(出示图2)这是两个“缺底”的圆柱,它们的表面积有什么关系?你会对比吗?
预设2:“折”的方法。
师:(出示图3)这两个“缺底”的长方体的侧面积有什么关系?你是怎样比的?
师:折出来的长方体与原本的长方形纸有什么联系?
师:还有其他的折法吗?什么样的长方形纸能折成正方体?
师:将长方形纸的一条边分成四份,可以折出长方体,那分成三份会折出什么图形?分成五份呢?八份呢?十二份呢?继续不停地分下去,折成的立体图形会接近什么图形?
师:这些立体图形有一个统一的名称,叫作直柱体。它们的侧面积都等于长方形纸的面积,可以用底面周“长×高”计算。
预设3:“转”的方法
师:(出示图4)将同一张纸绕不同的边旋转,得到两个圆柱,它们的侧面积相等吗?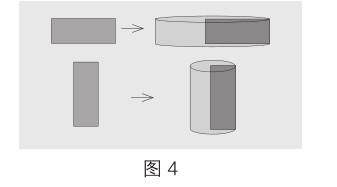
师:同一张纸,转出来的圆柱形状不同,侧面积却相等,这是为什么呢?
师:还能怎样旋转?怎样旋转体积最大?
师:如果将这张纸沿对角线剪开,得到直角三角形,旋转这个三角形会得到怎样的图形?
师:旋转后得到的圆锥,和刚才的圆柱之间有什么联系?
[设计意图:这一环节侧重通过操作帮助学生理解立体图形侧面积概念,梳理各种立体图形侧面积计算方法之间的联系。通过“卷”,帮助学生明晰侧面积的概念和计算方法;通过“折”,帮助学生理解侧面积等于“底面周长×高”,统一侧面积的计算公式;通过“转”,加深学生对圆柱侧面积计算公式的理解。从“卷”到“折”再到“转”,学生逐步探索,在操作中了解立体图形与平面图形之间的关系,沟通不同立体图形表面积的计算公式,优化认知结构。]
(二)研究立体图形的体积
师:(出示长方形从下向上平移的动态过程)将长方形从下向上平移,平移留下的痕迹也是立体图形。我们可以在头脑中想象一下,平移留下的痕迹是什么图形?(出示正方形、圆形从下向上平移的动态过程)将正方形、圆从下向上平移,分别会形成什么立体图形呢?
师:如果将三角形、梯形、正五边形为从下向上平移,平移留下的痕迹又会形成什么样的立体图形呢?这些通过平移得到的立体图形与平面图形之间有什么联系?
师:如果将正八边形、正十二边形向上平移,这个发现依然成立吗?它们的体积应该怎么算?
师:继续想下去,当被平移的正多边形的边数无限增多,我们会得到什么样的立体图形?
师:通过研究,我们发现这些直柱体的体积都可以用“底面积×高”来计算。在刚才的交流与分享中,我们又一次感受到了二维平面图形和三维立体图形之间的联系。这也说明,解决问题时,我们要用联系的眼光去分析。
[设计意图:该环节意在引导学生从运动变化的角度复习立体图形。学生通过想象平移留下的痕迹,感受立体图形底面积不变的情况下,体积的大小与高有关。在此基础上,学生通过平移,在想象中了解立体图形的特征,透过变化的表象去深究事物的本质,猜想、探究直柱体体积的计算方法。最后,通过问题“当被平移的正多边形的边数无限增多,我们会得到什么样的立体图形”,引导学生体会极限思想,逐步扩展认知结构。]
四、精选练习,巩固应用
全班交流推荐好题,分析解题策略。
师:立体图形在生活中有很多应用。你知道这些现象应用了立体图形的什么特征吗?
课件出示:(1)为什么牛奶盒是长方体,可乐瓶却是圆柱呢?(2)有关立体图形的表面积(侧面积)的实际问题中,有哪些典型的物体(比如通风管、金鱼缸)?可以怎么分类呢?(3)为什么要将快递盒拆开存放呢?(4)餐巾纸的包装有圆柱和长方体两种,它们之间有联系吗?
师:你在生活中还观察到了什么,爱思考的同学课后可以单独研究,也可以小组合作研究。
[设计意图:复习课的练习需要帮助学生深刻理解问题的本质,完善认知结构,获得自主复习的策略。课前的“好题推荐”,让学生分享他们认为的“好题”,意在让“不同学生得到不同的发展”,让推荐者和被推荐者都能在复习过程中有新的收获、新的认识,增加课的“厚度”;课后的“课题研究”,让学生带着观察的眼光、思辨的精神走出课堂,探索立体图形在生活中的应用,增加课的“长度”。这样的学习才是具有生长性的。]
(魏俊晨,江苏省南京玄武外国语学校附属小学,邮编:210009)

