找出线索,层层突破
从名侦探福尔摩斯、柯南,再到我国唐代名相狄仁杰,他们都有共同的特点:智商超群,善于推理,查谜案于无踪。为什么大家那么喜欢逻辑推理(常简称“推理”)故事呢?想必是那些悬疑丛生、谜团似锦的烧脑情节,激起人们对未知的好奇、对真相的探索、对正义的追寻。数学学科以抽象性、严谨性著称,逻辑推理能力是数学课程要培养的核心素养之一,无论是数学知识的产生和发展,还是人们对数学知识的理解和运用,推理都在其中扮演着关键的角色,没有严密的推理,就无法获得准确可靠的结论。推理训练题是培养学生逻辑思维、发展学生核心素养的有效载体。这里提供两道趣味性强、有一定挑战性的推理题,供读者参考。
【题目】
题目1 破译密码
乐乐放学回家,发现家门开不了,心想应该是门锁更换了密码。于是拿出手机赶紧给爸爸发信息。你能根据以下爸爸和乐乐的对话信息,成功破解密码吗?
乐乐:爸爸,你换了我们家门锁的密码了?
爸爸:是啊!
乐乐:新密码是多少?
爸爸:你不是总夸自己是小小福尔摩斯吗?给你两条线索,自己破译吧!
乐乐:哈哈,好嘞!
爸爸:这两条线索是——
樂乐:别卖关子啦!快点说。
爸爸:(1)密码是个四位数,我连续五次输入门锁密码,分别是:7152,9310,5274,2407,4721。(2)我每次输入的密码中有两个数字正确,但所在的位置都不对。
题目2 扑克牌游戏
扑克牌是一种大众娱乐工具。相传早在秦汉相争时期,大将军韩信为了缓解士兵的思乡之愁,发明了一种纸牌游戏。因为牌面只有树叶大小,所以这种游戏被称为“叶子戏”,后来纸牌发展成为现在的扑克牌。聪聪是玩扑克牌游戏的高手,一天,他设计了一个游戏和爸爸、妈妈一起玩。首先选择了16张牌,将牌摆在桌子上(如图1),随后聪聪从16张牌中记下一张牌,将点数告诉了爸爸,将花色了告诉妈妈。
聪聪:爸爸和妈妈,你们能从已知的点数或花色中推知我记下的这张牌是什么吗?
爸爸:我不知道这张牌。
妈妈:我知道你不知道这张牌。
爸爸:现在我知道这张牌了。
妈妈:我也知道了。
小朋友,听了聪聪爸爸和妈妈的对话,你能推出这张牌是什么吗?
【解析】
第1题,“破译密码”,听上去有一种侦探破案的感觉。侦探具有很强的逻辑推理能力,他们特别善于从细节中捕捉破案的关键信息,循此展开推理,作出判断。题目中给出了两条线索,需要学生判断从哪一条取得突破。第一条线索介绍了5次输入的密码,乍看好像推不出什么结论,可以先放在一边。再仔细研读第二条线索,根据“每次输入的密码中有两个数字正确,但所在的位置都不对”,一下子可以找到两个关键点,分别是“两个数字正确”“位置不对”,到底是哪两个数字正确呢?暂时看不出来,可以“位置”为突破口进行推断。先将5个数竖着排,便于观察:
这样,根据两条线索,抓取和解题有关的关键信息,思路就打开了。竖着排完以后,我们可以发现:2和7在每个位置都出现过,所以密码中不可能有2和7,我们就可以根据第二条线索,运用排除法,排除每个密码中的数字“2和7”,看剩下的数字是什么。根据7152这个数,可以知道密码中必有1和5,根据5274可以知道密码中必有5和4,根据2407可以知道密码中必有4和0,根据4721可以知道密码中必有4和1。从而得出密码是由0、1、4、5这四个数字组成的。最后再次竖着观察,用排除法来分析,得出密码是1045。有时候线索的顺序并不一定是“破案”的顺序,根据线索找到关键信息才能有效突破,“细节决定成败”用在“解题”中一样有用。可以引导学生进一步思考:聪明的小福尔摩斯,假如密码是5位,你能不能尝试编一道密码破译题,也向你的爸爸妈妈提出挑战呢?
第2题,聪聪设计的这个扑克牌游戏,要求从已知的点数或花色中推知心中想的这张牌,看似给了我们很多对话信息,可是容易被爸爸妈妈对话中的“不知道”“知道”弄迷糊。但细细来看,学生可以先从已有条件出发弄清题意,再逐条分析,抽丝剥茧地找到线索,完成推理。聪聪把点数告诉了爸爸,说明爸爸知道这张牌的点数;把花色告诉了妈妈,可见妈妈知道这张牌的花色。接下来可以把扑克牌游戏问题的这些条件转化为数学的表示形式,为方便观察和分析,可以把所有的图片信息转换成表格形式(如表1)。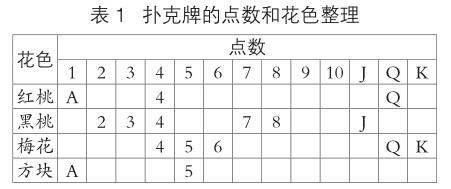
我们可以把聪聪爸爸妈妈的对话和表格中的数对应起来看。爸爸知道的是这张牌的点数,但他说“我不知道这张牌”,表明他不知道的是这张牌的花色。基于这样的理解,我们再去看表1,从中可以看出2、3、6、7、8、J、K这些数(J、K两个字母分别代表11、13)所对应的花色是唯一的,比如2,只有黑桃里面才有2。如果爸爸拿到了这些点数的牌,他必能直接判断这张牌的花色。但是爸爸说不知道这张牌,据此推理,可判断爸爸所知道的点数肯定不是这些数,那只能是A、4、5、Q这四个之一,因为这四个点数所对应的花色至少有两种(如表2)。比如A,红桃里面有,方块里面也有,只有这样爸爸才不会猜出这张牌的颜色。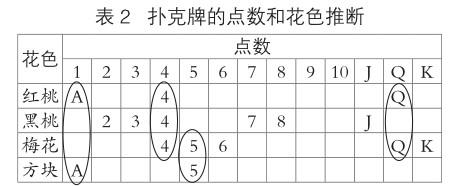
接下来从妈妈的话进行推理。她知道的是牌的花色,光凭花色就能很肯定地知道爸爸不知道,说明这个花色的所有牌的点数对应的花色都不止一种(否则知道点数的爸爸立即可以确定花色),可以断定不是黑桃和梅花,爸爸就可以推出这张牌可能是红桃或者是方块,即可能是红桃A、4、Q或者是方块A、5。再看第三句:现在我知道这张牌了,爸爸光凭点数就能知道,说明这张牌绝不可能是A,因为A有两张,不能确定是红桃还是方块。再次缩小范围,还剩红桃4、Q和方块5,最后一句妈妈说:我也知道了,妈妈光凭花色就能知道,说明这张牌一定是同花色只有一个点数的那张,就是方块5;如果是红桃,就不能确定是4还是Q了。
【设计意图】
逻辑推理属于逻辑思维范畴,是一种理性认识,是人们运用概念、判断、推理揭示事物本质和规律的认识过程,在人们的学习生活中占据重要位置。借助逻辑思维人们能预见事物的发展进程或现象将要发生的变化,作出合理、正确的判断和选择。逻辑思维是智力活动的核心成分,更是创造性思维的基础。我们可以通过创设具体情境、点拨推理方法等途径,进行推理训练,培养逻辑思维,提升数学素养。
一、创设具体情境,驱动逻辑思维
小学生的思维正处于从具体形象思维逐步走向抽象逻辑思维的阶段,往往需要在合适的情境或生活中感受和学习推理,驱动“逻辑思维”。数学中的逻辑推理训练,需要教师创设学生熟悉的现实生活情境和形象生动的数学情境,以具体情境中的事物为载体引导学生开展非形式化推理活动,目的是让学生认同逻辑推理这种思维模式。在上述两道题目中,笔者都尝试创设适合学生推理的具体情境,让学生自然进入逻辑推理环节。比如,第1题“破译密码”,利用学生生活中常遇到的忘记密码的情境,唤起学生想要“推理”的欲望,激起他们“推理密码”的冲动,让学生对对话中的数量关系作出思考分析,自然而然地开展推理,引发逻辑思维。再如第2题是从常见的扑克牌游戏进入推理环节,用学生熟悉的“扑克牌”设计了与以往不同的游戏,激发学生去探索、思考游戏结果,这就埋下了“推理”的种子。
二、点拨推理方法,发展逻辑思维
逻辑推理的基本步骤,就是根据已知的条件或前提,推断出结论。当学生把现实生活或具体情境中的问题转化为数学问题时,就进入到数学推理环节,这时需要运用多种操作和推理方法,而由于各种制约因素的存在,学生的方法积累相对不足,需要教师适时给学生提供方法指导,满足不同学生群体的学习需要。小学生的思维特点,决定了推理能力的培养应当充分运用直观、数形结合等方式,强化操作、实验、猜想、验证中的数学思考,从多方面促进理解、推理与表达。此外,推理需要运用敏锐的观察力和洞察力展开深入思考和想象,才能形成丰富推理成果。比如,在第1题中,对于给出的两条线索,如果按照顺序,不一定能找到解题的思路,仅凭第一条线索得不到更多有用信息,此时,可以把该线索暂时搁置,引导学生从另外的线索中找到“两个数字正确”“位置不对”两个关键信息,从细节入手合理推断,理清思路,按顺序纵向列举,通过观察数字特征进行理智、系统的分析。再如,在第2题中,面对所列出的一大堆扑克牌,可引导学生先将现实问题转化为数学问题,用符号语言和图形语言把抽象的问题具体化。采用列表的方法,能够清晰地看到对应的花色和点数,再根据对话中的表述,引导学生充分思考,逐条分析。每选择1条信息,可以有2种推理方法,既可以从信息中找到符合条件的一些数或花色,也可以通过信息排除一些干扰,逐步缩小范围。同时要注意关注逻辑顺序。如,妈妈的表达之所以正确,是建立在“爸爸的表达是正确的”这个前提下。让学生知道,前提是论证的基础,推理常常是一环扣一环的。需要找出线索,再通过推理层层突破。
小学生正处于逻辑思维发展的启蒙阶段和黄金时期,教师可以有意识地进行推理训练,培养学生的逻辑思维能力,提高思维的灵活性与严谨性,发展学生的数学核心素养。
(徐妍,江苏省南京市长江路小学,邮编:210018)

