数学文化素养话题之九：神奇的莫比乌斯带

刘劲苓 石雪纳 裴杰

刘劲苓：艺术是人类对世界的感性认知，而数学是人类对世界的理性认知。有人认为，数学家通过右脑工作，艺术家则通过左脑工作。数学和艺术，一个逻辑严谨，一个感性浪漫，完全不可能共生共存。但是，艺术和数学实际上是密不可分的，正如科学家开普勒所说，“数学是一切学科的基础”，而数学家哈尔莫斯也认为，“数学是一种别具匠心的艺术”。

石雪纳：“数学是一切学科的基础”，这已经成为大家的共识。刘老师，说到数学与艺术的完美结合，我想到了一位荷兰版画艺术家——埃舍尔。埃舍尔的作品不仅呈现了视觉上的美感，也具有丰富的数学内涵。（出示图1）这幅作品看起来像两队人马往相反方向行进，但其实他们都处于一个面上，是沿同一方向行进的，很是神奇！这幅作品隐藏着怎样的数学奥秘呢？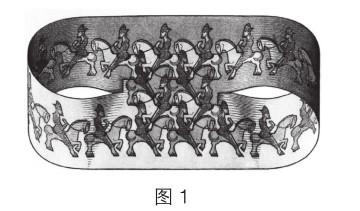

刘劲苓：这幅作品其实是运用了数学中莫比乌斯带的神奇特性！有人说莫比乌斯带是科学艺术的怪圈。这个怪圈是由德国数学家莫比乌斯发现的，它只有一个面和一条边，数学中将这样的面叫作单侧曲面。莫比乌斯带是拓扑学中最有趣的单侧曲面之一。说到“拓扑学”，它也是数学中的一个重要分支，主要研究几何图形在连续变换下的一些不变特征和规律。埃舍尔的这幅作品，画的其实就是一队人马在莫比乌斯带上行进。

石雪纳：将一张长方形纸条按通常的方式首尾相接，我们会得到一个普通纸圈，纸圈有上下两条边，内外两个面。如果一只手捏住纸条的一端不动，另一只手把纸条的另一端扭转半周（180°），再把纸条首尾相接，就能得到另一种纸圈——莫比乌斯带（如图2），它只有一个面和一条边。

刘劲苓：如果我们从莫比乌斯带面上的某一点开始涂颜色，笔不离开纸面，也不跨越纸圈的边缘，一直画下去，就会不知不觉地回到出发点；同样地，从莫比乌斯带的边上的某一点出发，沿着边画过来，最终也会回到起点。这些奇怪的现象在普通纸圈上是绝对不可能发生的，除非你跨越纸圈的边缘。

石雪纳：刘老师，莫比乌斯带这么神奇，是怎样被发现的呢？

刘劲苓：莫比乌斯带的发现源于一个古老的问题：世界上有没有只有一个面、一条封闭曲线做边界的纸圈呢？这个问题引起了莫比乌斯的注意，他长时间地研究和试验，但总是毫无结果。传说有一天，工作了一整天的莫比乌斯感到有些疲惫，便到郊外散步。他来到玉米地，看到一片片肥大的玉米叶子在微风中忽而伸直，忽而卷起，玉米叶子在他脑海里变成了一张张纸条。于是他蹲下身去，撕下一片叶子，顺着它卷起的方向把它首尾相接成一个“圆圈”，“啊！”他惊叹道，“这不就是我梦寐以求的那种圈吗！”于是，莫比乌斯忘记了劳累，兴奋地跑回办公室，裁出纸条，把纸的一端扭转180°，再将一端的正面和另一端的背面粘在一起，做成了一个只有一个面的纸圈。纸圈做成后，莫比乌斯捉了一只小甲虫，让它在纸圈上面爬。结果，小甲虫不翻越任何边界就爬遍了纸圈的所有部分。莫比乌斯激动地说：“公正的小甲虫，你无可辩驳地证明了这个纸圈只有一个面。”莫比乌斯带就这样被发现了。

石雪纳：没想到，莫比乌斯带的发现，这么富有神奇色彩！

刘劲苓：莫比乌斯带还有许多神奇、有趣的特性呢！猜一猜，如果沿莫比乌斯带中线剪开，会有什么样的结果出现呢？

石雪纳：我猜应该是形成2个圈吧。

刘劲苓：动手剪一剪，你会发现，沿莫比乌斯带中线剪开，它会变成1个大圈，并且不是普通的纸圈，也不是莫比乌斯带，而是一个扭转了360°的新型纸圈！

刘劲苓：我们可以试试看！如果沿与边平行的方向把莫比乌斯带的面三等分，画出两条三等分线，再用剪刀沿这两条线剪开——出人意料的是，剪刀绕了两个圈竟然又回到原出发点！猜一猜，剪开后的结果是什么，是一个大圈？还是三个圈？

石雪纳：是一个更大的圈吗？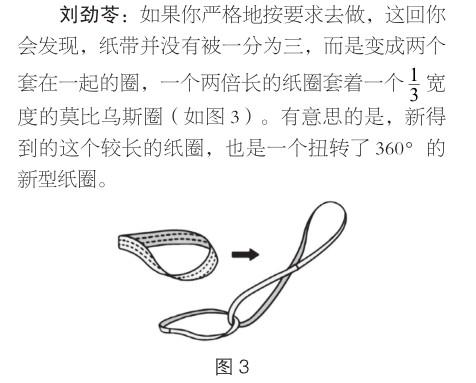

石雪纳：刘老师，这个莫比乌斯带真的挺神奇，每一次剪，都能得到意想不到的结果！怪不得被称作怪圈呢！继续探索下去，还会有什么新的结论出现呢？

刘劲苓：你可能已经注意到了，莫比乌斯带有一条非常明显的边界，这使人感到美中不足。德国数学家费利克斯·克莱茵把两条莫比乌斯带沿着它们唯一的边界粘贴起来（在四维空间中才能完美地完成这个粘贴），找到了一种自我封闭且没有明显边界的模型，这就是著名的克莱因瓶（如图4）。反过来，如果把一个克莱因瓶按某种方式剪开，我们会得到两条莫比乌斯带。如果把适量的水倒入克莱因瓶中，水会流入这个瓶的底部，但如果想把水倒出来，逆时针旋转180°是不行的，而是需要顺时针旋转同样的度数。大家可以想象一下，有条件的也可以动手操作一下试试。

石雪纳：听了您的介绍，越发觉得莫比乌斯带真神奇！其实，莫比乌斯带已被广泛地应用在我们的生活中，但一般人并未注意到。例如，它被用于制作机械传送带，比传统的传送带更均匀，在防磨损和撕裂方面的表现更佳，使用寿命也更长。它还被用于制作录音带和录像带。最早的用于录音的莫比乌斯带是由弗利斯特于1923年设计出来的。

刘劲苓：莫比乌斯带循环往复的特征，蕴含着永恒、无限的意义，因此也常被用于各类标志设计。2010年，中国上海世界博览会湖南馆设置了两个互相嵌套的大型“莫比乌斯环”，在这两个无始无终的单侧曲面上，投映着湖南省的历史与未来，寓意人类对未来的期盼和追求永不停歇。艺术创作中，莫比乌斯带就出现得更频繁了。例如，瑞典在1982年发行了根据莫比乌斯带的原理设计的邮票，前面提到的艺术家埃舍尔还把莫比乌斯带用来创作他的木刻画《莫比乌斯带Ⅰ》和《莫比乌斯带Ⅱ》。

石雪纳：确实，莫比乌斯带看似简单，然而又极其深刻。它有那么多美妙的应用，又不断启发新奇的想象。莫比乌斯带堪称“数学的艺术形象”，也是“艺术形象的数学”。那么，数学课堂中应如何引领学生感受莫比乌斯带的神奇，体会它的艺术之美呢？我校的裴杰老师对此也有很多想法，我们将她邀请来一起讨论。

裴杰：大家好。

刘劲苓：对小学生而言，探讨莫比乌斯带的更多特性显然不合适，但“在操作中体验”符合小学生的天性。大多数教师教学这个内容时，就是让学生在玩中体验莫比乌斯带的神奇。

石雪纳：我在三年级教学时是这样引入的：

师：刚才大家都说了假期中印象最深的事，老师印象最深的就是和我们家小孩在小区里玩小蚂蚁的事。我们拿了一张这样的长方形纸，把蚂蚁放在上边，你觉得它会怎么样？（学生回答：爬走）它只要爬到边缘，我们就把它赶回到纸面上，照这样玩下去，这个蚂蚁能爬到纸的反面去吗？（学生回答：不行）因为一到边缘我就把它赶回去了。那有没有什么办法，不让蚂蚁跨过纸条的边缘，却能够爬到反面？拿出你的纸条，试一试。

（学生用手里的纸条动手操作。）

师：你是怎么折的？举起来给大家演示一下。

生：我就是先拿这一头，再把另一头折反过来一下，然后把这两头对在一起（首尾相接）就行了。

裴杰：石老师是结合生活情境，通过问题“怎么让小蚂蚁不跨过纸条边缘，却能够爬到反面”引领学生动手尝试，一步步走进莫比乌斯带的。我的教学对象是六年级学生，所以引入方式和您不太一样。

师：今天裴老师给大家带来一个魔术。这是一个纸圈，如果我沿着它的中间剪开，（剪了一段后）你们猜，剪开后会变成什么样子？（学生回答：两个圈）你们想的究竟对不对呢？我们剪开看看。（教师剪完后，学生发现得到的还是一个圈）看了这个魔术你们有什么感受？

生：我觉得剪开应该是两个圆环，为什么剪开是一个大圆环呢？

师：同学们真爱动脑筋！大家不只在欣赏这个小小的魔术，还在思考它背后的道理，特别棒！其实裴老师拿的这圈可不是一般的圈，它有个特殊的名字——莫比乌斯带，也叫莫比乌斯圈。

石雪纳：用魔术的方式引入确实更能引发学生的好奇和思考。

刘劲苓：其实，无论怎样的引入方式，目的都是激发学生继续探究的意愿和兴趣。

石雪纳：是这样的！裴老师，学生做出来莫比乌斯带之后，您是怎么引导学生继续探究的呢？

裴杰：接下来，我请学生在小组内交流自己发现的莫比乌斯带的特点。讨论之后的汇报层次性更强，让我们一起来看看他们课堂上的汇报：

生：通过刚才的实验，我们发现莫比乌斯带有两个特别有意思的特征，我讲解的同时，我们组的其他同学演示。首先，莫比乌斯带只有一个面。（2个学生配合演示，一人拿着莫比乌斯带，另一人用笔在上面画）从莫比乌斯带上的一个点开始，一直往下画（不跨面），直到回到原点。这条线经过莫比乌斯带上所有的面，且首尾相接。第二个有意思的特征是，莫比乌斯带只有一条边。（2个学生配合演示，一人拿着莫比乌斯带，另一人用手指）从一个点开始，手指沿莫比乌斯带的边一直走，手指会回到原点，并且经过了莫比乌斯带的所有的边。

生：莫比乌斯带是一个立体图形，我觉得它应该有两个面和两条边呀？

生：莫比乌斯带最初是一张纸条，有正反两个面。一面是花面，一面是白的。我们把花面和白面连接到了一起，所以就变成了一个面。

生：（边展示边说）我把纸条一边涂成红色，一边涂成黑色，因为它“扭”了一下，所以黑边和红边就连在一起了，沿任意一边走一圈，就能把黑边和红边都走过，所以莫比乌斯带只有一条边。

刘劲苓：六年级学生的观察思考是比较全面和深刻的。

裴杰：是的。学生在画一画、描一描、剪一剪的过程中，认识莫比乌斯带，感受莫比乌斯带的神奇。

刘劲苓：这里我还要特别强调一点，剪之前的猜测很重要。学生剪完后发现结果与猜想的不一致，才会更加好奇，激发继续探究的愿望。

石雪纳：除了要关注猜想，还要让学生感受、体会莫比乌斯带的用处和它的艺术之美。在课的最后，我是这样处理的：

师：德国数学家、天文学家莫比乌斯发现了这个神奇的纸圈，当时的人们对它产生了很大的兴趣，纷纷开展探究，就像刚才大家的操作一样。那这个莫比乌斯圈有什么用啊？你觉得它可以用在哪儿？

生：我觉得可以做一个莫比乌斯带滑梯，就可以一直滑，滑不完了。

生：还可以做莫比乌斯带过山车。

师：莫比乌斯带过山车，还真的有！在美国肯尼森林公园，有一个叫云霄飞车的过山车就是利用莫比乌斯带的原理造的。

生：可以做一些高难度的迷宫。

师：哦，用莫比乌斯带做成高难度的迷宫来锻炼思维。对吗？还有吗？

生：我觉得咱们买饮料的时候，服务员可以把吸管挝成一个莫比乌斯带，就很美观。

生：这个吸管怎么用啊？岂不是一直喝不到？

……

师：刚才有同学说做成滑梯，对吧？（课件出示莫比乌斯爬梯）还真有，不过不是滑梯，是爬梯。就在咱们西城区，但是很遗憾，因为喜欢它的人太多了，现在这个爬梯已经被玩坏了。生活中还有很多的地方可以用到莫比乌斯带，（课件出示传送带）1979年，美国的一个轮胎公司把传送带做成莫比乌斯带的样子。不止这些，（课件出示针式打印机）还有针式打印机的色带，也做成莫比乌斯带的形式。想想看，这样做有什么好处啊？

生：这样不光正面能用，反面也能用。

师：充分利用每一个面，使各个面发挥它最大的作用，从而达到节约材料、延长使用寿命的目的。莫比乌斯带这样循环往复，给人一种永恒、无穷无尽的感觉，所以在一些美学设计上，就用到了它。（课件出示项链图片）这是一些根据莫比乌斯带设计的项链。（课件出示图书馆照片）哈萨克斯坦正准备建一个新的国家图书馆，它的外观就是以莫比乌斯带为灵感设计的。（课件出示邮票）1982年，瑞士发行了一枚这样的邮票，它也是根据莫比乌斯带原理来设计的。

刘劲苓：这样的教学是比较完整的。事实上，我们还可以找到更多有艺术效果的图片，课堂上请学生欣赏和感受。不过没关系，课堂难免留下遗憾。因为遗憾，我们才会有改进的方向和努力的动力。让我们在学习中不断完善自己，不断将数学文化传播开来。

石雪纳：非常感谢刘老师的建议！我们会在相互学习中完善自己，让数学文化走进课堂，走进学生的心灵深处。

（刘劲苓，特级教师，北京市西城区教育研修学院，邮编：100031；石雪纳，裴杰，北京第二实验小学，邮编：100045）