不确定浅海环境中水平阵角度域子空间检测*
王宣 孙超† 李明杨 张少东
1) (西北工业大学航海学院,西安 710072)
2) (陕西省水下信息技术重点实验室,西安 710072)
3) (浙江大学信息与电子工程学院,杭州 310058)
在复杂浅海波导中,环境参数的不确定性影响检测的稳健性,故稳健检测是浅海检测中的重要问题.本文结合简正波模型,定义和估计了不确定环境中的水平阵角度域子空间,提出了水平阵角度域子空间检测器及其稳健形式.角度域子空间利用了不同环境参数条件下的水平阵远场观测模型,包含了不确定环境参数信息,估计过程中利用了硬海底条件下传播模态的水平波数与水体、沉积层声速之间的关系,具有较少的先验信息要求和较低的实现复杂度.在此基础上提出的水平阵角度域子空间检测器实现简单,在不确定环境中具有一定的稳健性,但其检测性能随目标方位角起伏.将角度域子空间变换到维数恒定的子空间中,得到角度域子空间检测器的稳健形式,即稳健水平阵角度域子空间检测器,该检测器在不确定环境中具有一定的稳健性,同时检测性能在各目标方位上一致.不确定浅海环境中的仿真结果表明,稳健水平阵角度域子空间检测器具有和能量检测器近似的稳健性,同时提高了检测能力.
1 引言
浅海环境中,多变的水体声速剖面和复杂的海底底质导致波导的起伏多变[1],给水下目标的检测带来困难.水平线列阵(horizontal linear array,HLA)是一种具有水平孔径的水听器阵列,被广泛应用于测向、波束形成等领域[2,3],其孔径不受海深的限制,可以通过增加阵元的方式提高阵列信噪比,将其固定布放于海底时,还可以减少风浪等因素对阵形的影响,这两个优势使得HLA 可以在较为复杂的浅海环境中获得较好的检测性能.
HLA 的接收信号模型可由水下声传播模型建立[3−6],当环境参数不确定时,结合先验信息和水下声传播模型可以得到多种宽容检测方法,如贝叶斯检测方法、广义似然比检测方法、子空间类检测方法等.贝叶斯检测方法利用了不确定参数的分布信息,具有统计上最优的检测性能[7];广义似然比检测方法利用了参数不确定范围信息,检测性能趋近贝叶斯检测方法[8].但这两种方法在部分参数条件下会出现信号波前失配的情况,导致稳健性不足.子空间类检测方法通常具有更高的稳健性,被广泛应用于水下检测[9−13].其中,李明杨[11]通过信号波前矩阵构建了包含不确定环境信息的子空间,并提出了不确定环境中稳健的子空间检测器,该检测器在不确定环境中具有接近能量检测器的稳健性.但是HLA 的信号特征子空间维数较大,而子空间类检测器的检测性能与所利用子空间的维数成反比,则该子空间检测器用于HLA 时检测能力偏低.常见的改进方法是通过截断信噪比较低的子空间成分[14],降低子空间维数,提高检测器的检测能力.但信号特征子空间中信噪比较低的成分无法确定,任意截断子空间会导致在部分参数条件下信号投影能量损失过大,与稳健需求相矛盾.
本文在简正波模型的基础上,结合HLA 远场观测矩阵和不确定环境参数,定义了不确定环境中的HLA 角度域子空间.在不同环境参数条件下,HLA 接收到的信号均能落入该子空间中,表明该子空间在不确定环境中具有很高的有效性.因为HLA 远场观测矩阵是对简正波中行波信息的采样,而采样到的行波相关性较高[15],所以角度域子空间具有较低的维数.理想的角度域子空间的构造中需要利用所有的不确定环境参数,在实际中是无法实现的,需要对角度域子空间进行估计.本文结合硬海底环境中可远场传播模态的水平波数与声速剖面间的关系,提出角度域子空间的估计方法,该方法只需要海底声速和沉积层声速的不确定范围信息,降低了先验信息的要求,同时通过波数采样的形式,避免了对各环境的水平波数的计算,降低了计算复杂度.在角度域子空间估计的基础上,结合子空间检测思想[12]和广义似然比检测中不确定参数的优化方法[8],本文提出了水平阵角度域子空间检测器(HLA angle-domain subspace detector,HASD).因为角度域子空间包含了不确定环境信息,在任意环境参数条件下均能近似完整地利用信号能量,所以HASD 在不确定环境中具有一定的稳健性.
受角度域子空间维数变化的影响,HASD 检测概率在水平方位上存在较大的起伏,使得HASD在不同方位的检测中稳健性不足.本文对影响角度域子空间维数的因素进行分析,通过将角度域子空间变换到恒定维数的子空间中,构造了新的角度域子空间,并提出了HASD 的稳健形式,即稳健水平阵角度域子空间检测器(robust HLA angle-domain subspace detector,RHASD).RHASD 在不确定环境中和不同目标方位时均具有稳健的检测性能.
本文其他部分安排如下:第2 节结合海洋波导中传播模态的特性,定义了不确定浅海环境中HLA 角度域子空间并给出其估计方法;第3 节提出了HASD 检测方法及其稳健改进RHASD,分析了两种方法的稳健性;第4 节通过仿真实验分析了HASD 和RHASD 的检测性能,并与几种宽容检测方法进行了对比;第5 节给出相关结论.
2 不确定浅海环境中HLA 角度域子空间估计及其有效性量度
2.1 HLA 接收信号模型
在浅海波导环境中,深度为zs的单频点源与远场 (r0,z0) 之间的传递函数可以表示为多阶简正波叠加的形式[4]:

式中,Φ表示海洋环境参数集,通常包含水体声速剖面、水体深度、水体密度、沉积层声速、基底声速、沉积层密度和吸收系数等海洋环境参数;M表示该环境下声源激发的传播模态数;km和ψm分别表示Φ条件下第m阶传播模态的水平波数和模态函数;ρ表示水体密度.
布放在za深度处的N元HLA 各阵元与远场声源间的水平距离可以近似为

式中,rs表示阵中心与第1 号阵元间的水平距离;d表示阵元间距;θs表示目标方位.目标声源与HLA 的空间关系如图1 所示.图中Oxy表示海平面,z表示深度,S表示声源.将(2)式代入(1)式,可以得到HLA 各阵元与声源间的传递函数:

图1 目标声源与HLA 空间位置关系Fig.1.Geometric relationship between target sound source and HLA space.

式中,g为N ×1 维列向量,上标 T 表示转置.那么,HLA 的频域接收模型可以表示为

式中,r,s,n均为N ×1 维列向量,分别表示阵列接收数据、声源辐射信号和背景噪声;a0表示目标声源的复幅度.假设背景噪声为空间白噪声,服从n ∼CN(0,2σ2IN),其中 2σ2表示单个阵元上的噪声功率.定义阵列信噪比SNR 为阵列接收到的信号能量与单个阵元上的噪声功率之比,其分贝表示形式为,其 中∥·∥2表示向量l −2范数.
2.2 HLA 角度域子空间及其估计
对于浅海波导环境中的远场单频点源,HLA接收到的声源辐射信号s可以近似表示为[6]
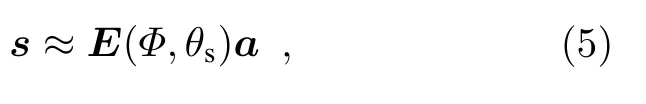
式中,


E(Φ,θs)为N ×M维的HLA 远场观测矩阵[3,6],表示各阵元对M阶模态行波的采样[15];a=[a1,···,aM]T为M ×1 维列向量,表示HLA 各采样行波的复幅度.
定义不确定海洋环境中的HLA 角度域子空间W(θs):
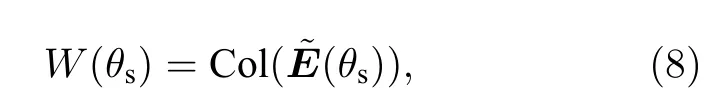
式中


即对于任意环境参数条件和任意目标距离和深度条件,s均近似位于目标水平方位角θs对应的角度域子空间W(θs) 中.
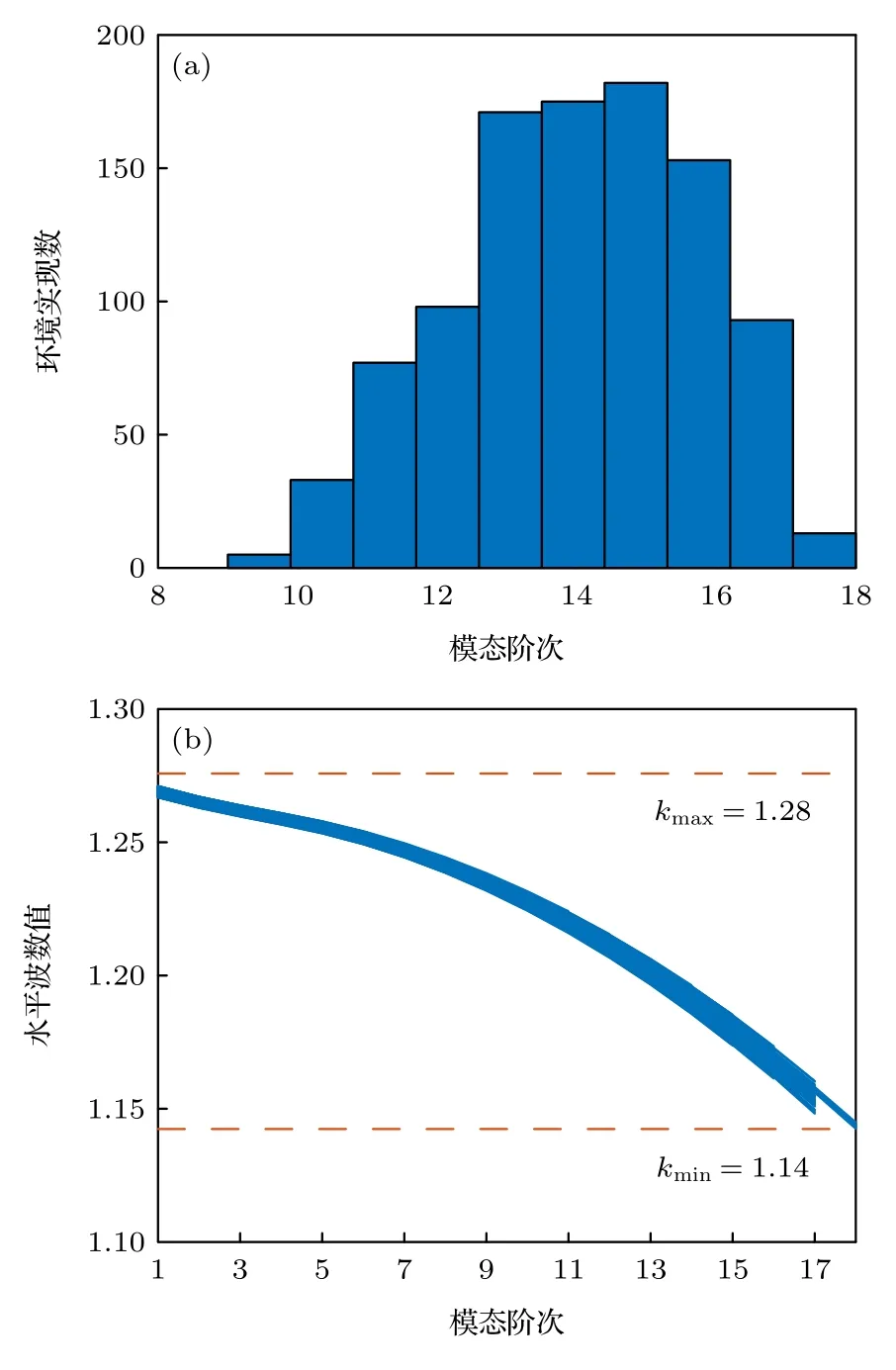
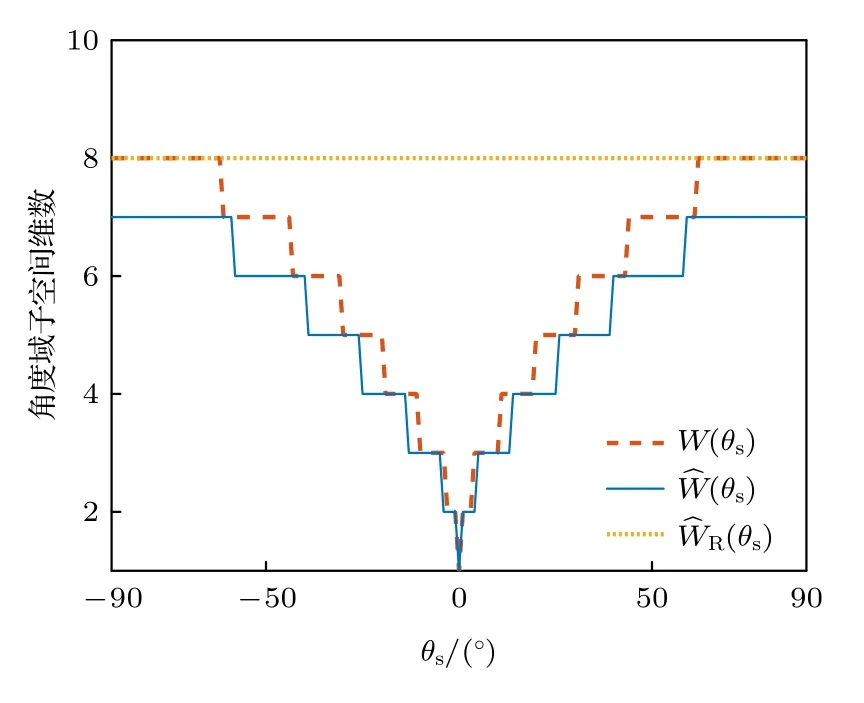
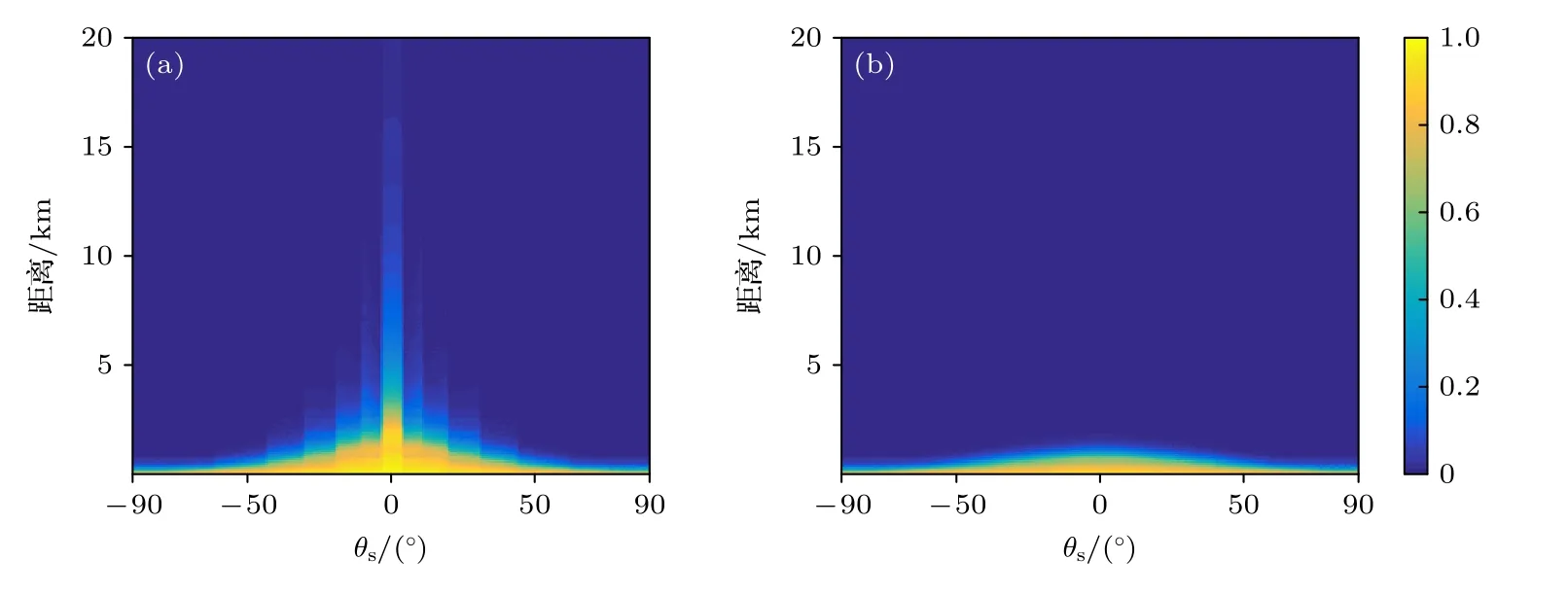
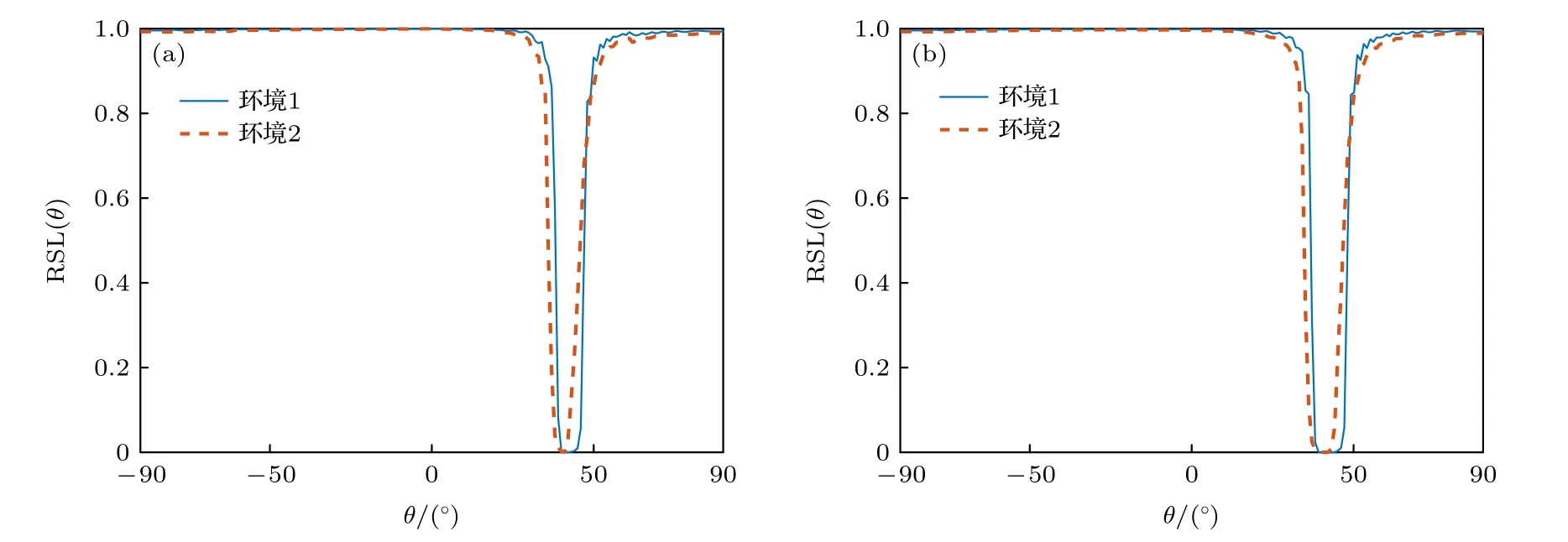
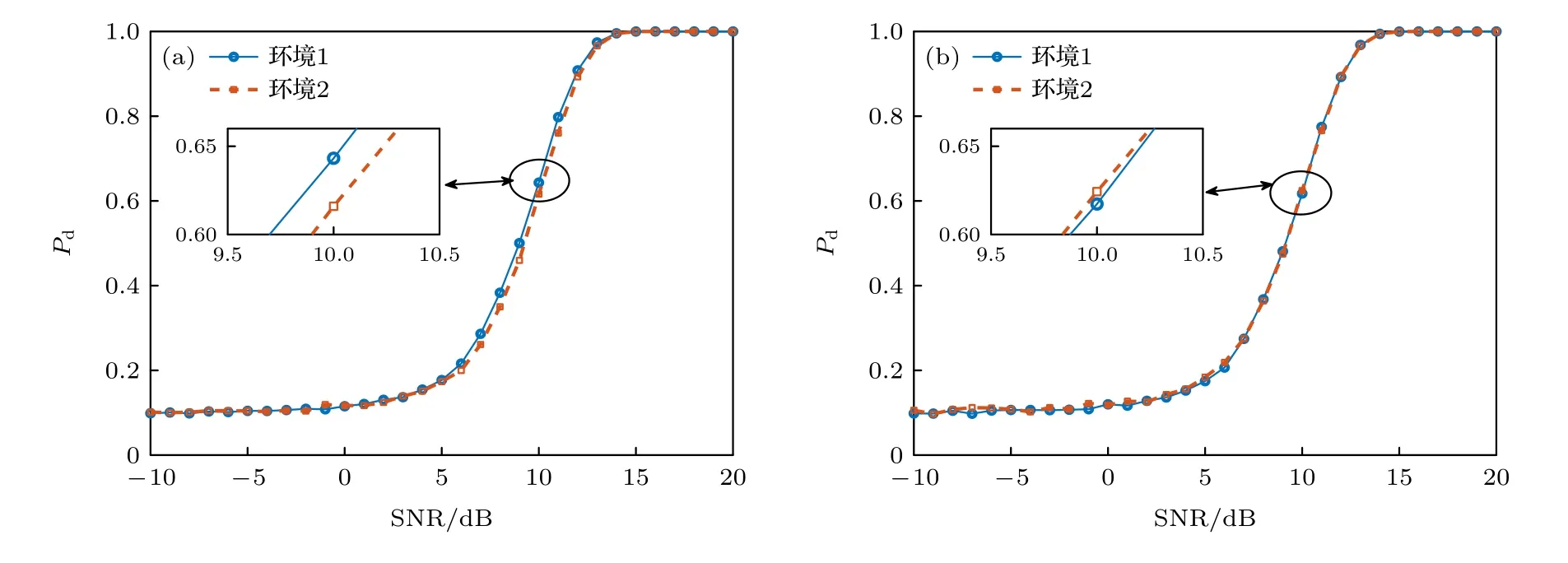
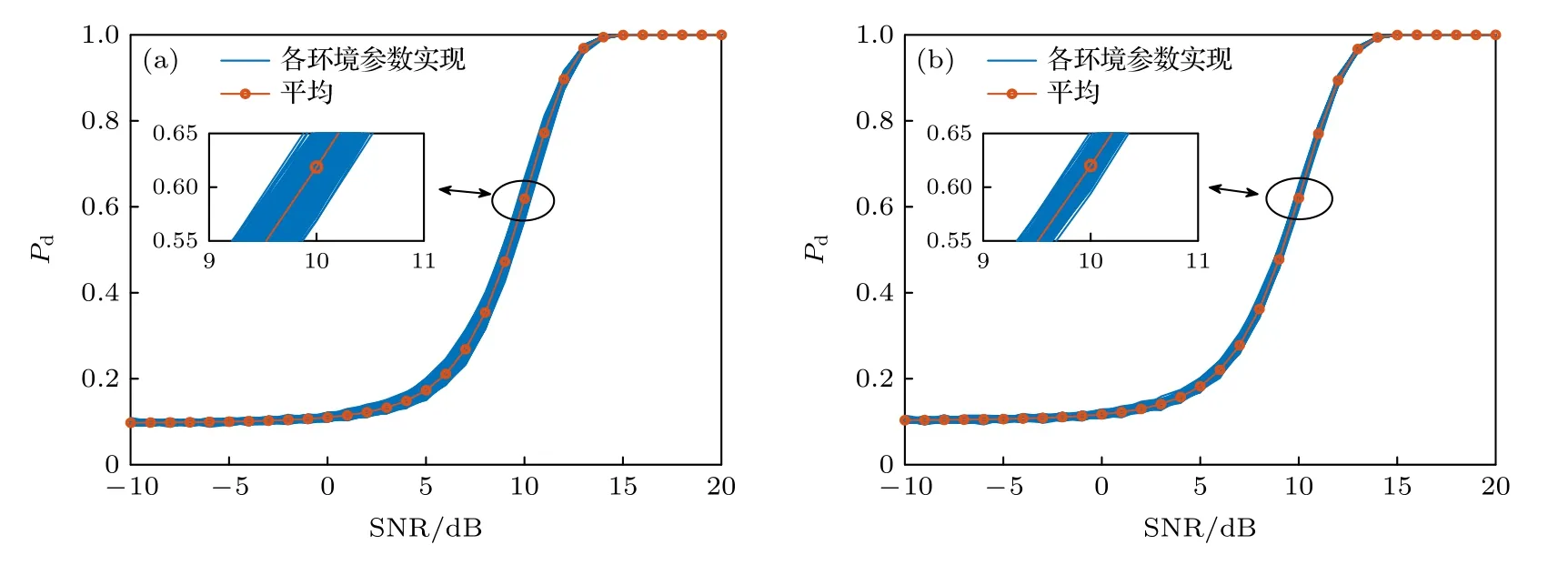
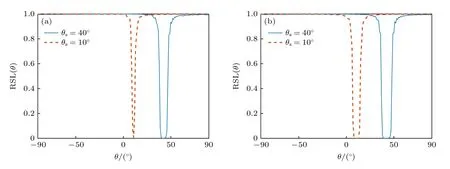
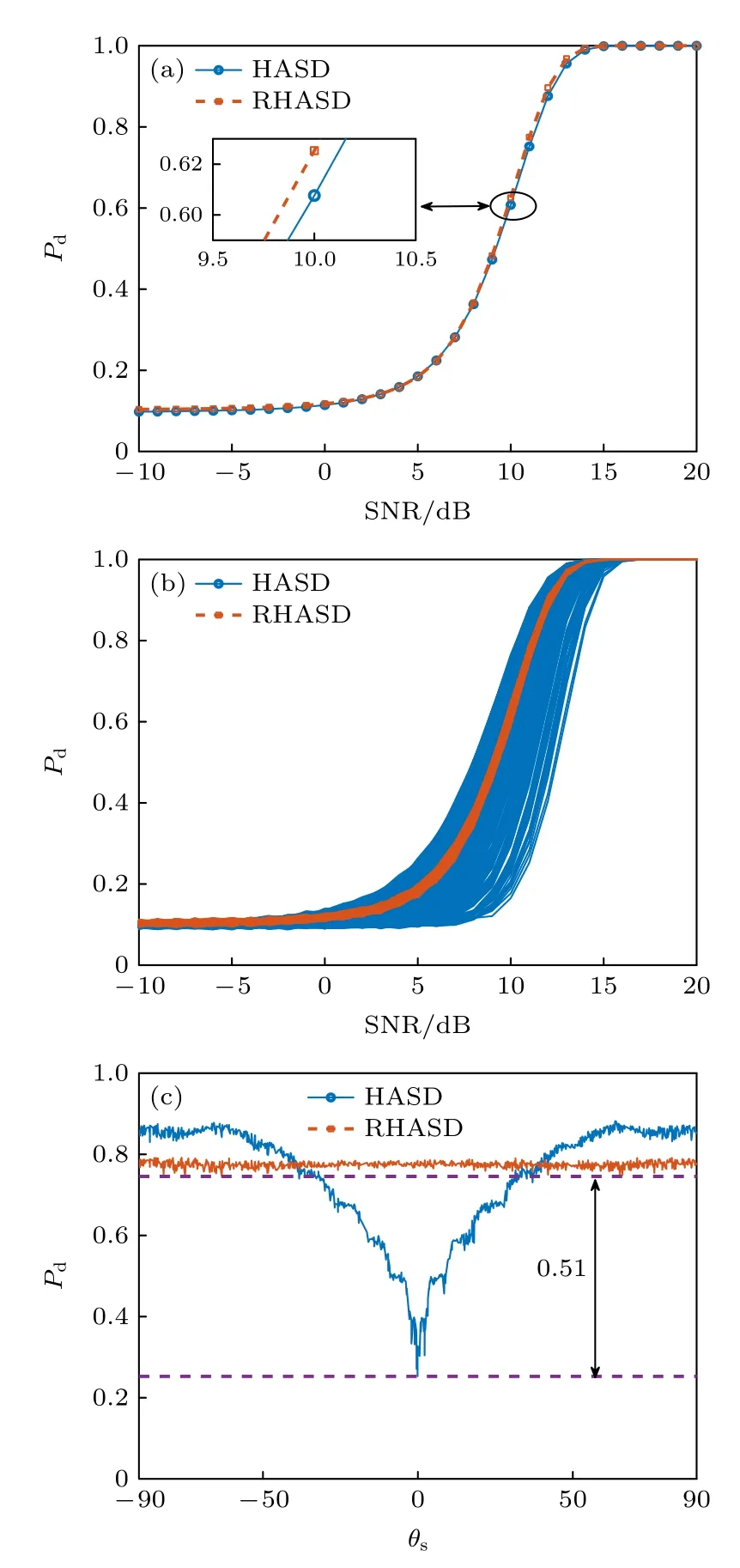
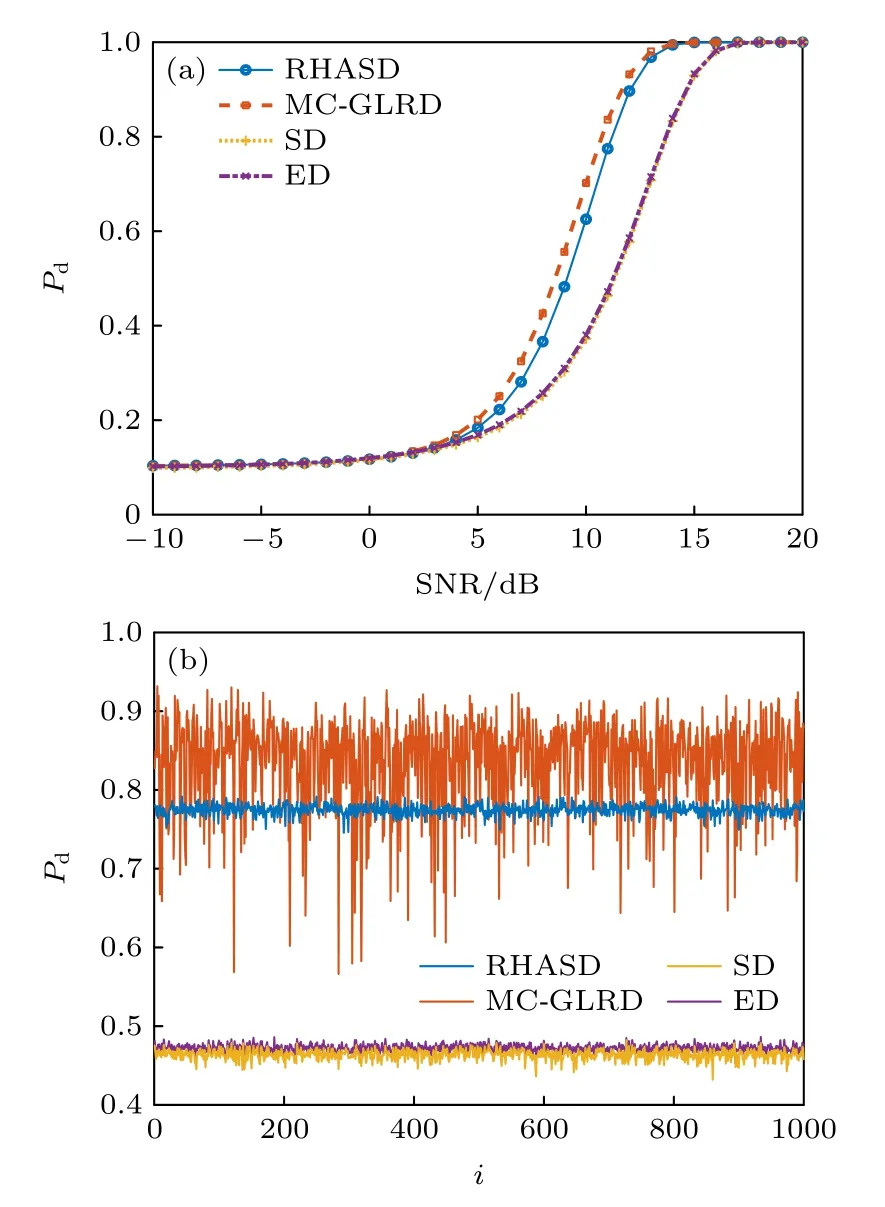
理想的角度域子空间W(θs) 需要利用所有可能的环境参数集,在实际中无法获得,这使得角度域子空间W(θs) 难以利用,因此需要对W(θs) 进行估计.图 2 为美国1993 年NRL 使用的浅海标准失配测试模型[1],图中各参数意义及不确定范围如表 1 所列.图 2 所示环境为硬海底环境(沉积层声速大于水体声速),水体中声速剖面为负梯度,根据简正波理论[4]中水平波数范围可知,可远场传播的模态(陷获于水体中的模态)对应的水平波数满足kd 图2 浅海标准失配测试模型Fig.2.Standard mismatch test model in shallow-water. 表1 浅海标准失配测试模型中参数意义及取值范围Table 1.The value range of standard mismatch test model. 式中,kmin=2πf/max{cd},kmax=2πf/min{cb}.在(kmin,kmax)中Z次等间隔采样并构建矩阵′(θs), 式中,上标 H 表示共轭转置运算.U(θs),Λ(θs),V(θs)分别表示有效秩K(θs) 对应的左奇异向量矩阵、奇异值对角矩阵、右奇异向量矩阵.为了保证子空间投影过程中信号能量损失较小,有效秩可以由 Frobenius 范数比的平方ν2确定: 式中,λ1,···,λK(θs)表示前K(θs) 个大奇异值,λ1,···,λN表示全部N个奇异值,是接近1 的阈值.将(14)式和(13)式代入(10)式可得: 式中,b=显然,HLA 接收到的信号s可以由矩阵U(θs) 各列向量线性表示,将矩阵U(θs) 张成的Kθs维空间作为角度域子空间的估计, 其中,U(θs) 的列向量为的一组标准正交基.结合(11)式和(12)式可知,与cb和cd之外的海洋环境参数无关,降低了对先验信息的要求.同时,波数采样的方式避免了求解不同环境参数对应的水平波数,降低了实现复杂度. 式中,P=U(θs)UH(θs),表示的正交投影矩阵;RSL(θs) 表示s正交投影至过程中损失的信号能量与总信号能量的比值,值域为 [0,1] .RSL(θs)=0时,表明投影过程中无信号能量损失;RSL(θs)=1时,表明投影过程中信号能量完全损失.当cb和cd的先验信息准确且Z足够大时,任意环境参数条件下均能满足 RSL(θs)≈0,此时在不确定环境中具有较高的有效性. 对不确定浅海环境中的远场单频点源检测问题,可以建立频域检测模型: (19)式描述了一个二元假设检验问题,H0为0 假设,表示只存在噪声;H1为备选假设,表示存在信号和噪声. 根据角度域子空间的分析可知,HLA 接收到的声源辐射信号s近似地位于中,将(16)式代入(19)式,则两种假设下的似然函数为 两种假设下的条件似然比可以写为 检测过程中目标方位往往是不确定的,故θs是未知参量.由前文的推导过程可知,b与目标位置及环境参数有关,故b同样为未知参量.分两步分别求得b和θs的最大似然估计值: 式中,θ是搜索参量,C=[−90◦,90◦] 为θ的搜索区间.将(22)式代入(21)式并取自然对数,在此基础上,本文提出HASD,其检验统计量为 式中,TH(r) 表示C范围内,接收数据在角度域子空间上的正交投影能量与噪声功率的最大比值. HASD 的检验统计量在两种假设下分别为 将H1假设下的检验统计量改写为 式中l(θ) 满足 式中K(θ) 为角度域子空间的维数,表示自由度为 2K(θ) 的非中心化卡方分布,非中心化参量 与接收信号s在角度域子空间中的正交投影能量成正比.结合(18)式,将(27)式表示为 式中,RSL(θ) 表示s正交投影至的相对能量损失.结合(25)式、(21)式、(28)式可以看出,HASD的检测性能受{RSL(θ)|θ ∈C}和阵列信噪比的影响. 由第2 节分析可知,当θ=θs,任意环境参数条件下 RSL(θ)≈0 .而当θ逐渐远离θs,的列向量与的列向量间相关性迅速下降,RSL(θ)迅速增大至1.给定一个接近0 的量ϵ,定义θs的邻域C1(θs)={θ|RSL(θ)<ϵ},使非中心化参量满足 将H1假设下的检验统计量进一步改写为 式中 Tn对应的各非中心化参量近似为0,没有包含信号信息,而Ts对应的各非中心化参量大于0,包含了信号信息,是影响TH(r)|H1的主要因素. 假设阵列接收信噪比和目标方位不变,当环境参数改变,C1(θs) 变化较小,Ts和Tn分布的变化较小,表明HASD 的检测性能在不同环境参数条件下具有一定的稳健性.而当目标方位由±90◦趋近0◦,矩阵列向量间相关性上升导致的维数K(θs)减小.而K(θs)减小使Ts中各卡方分布的自由度减小,导致Ts的右尾概率降低,进一步使TH(r)|H1的右尾概率降低,导致HASD 的检测概率降低.这意味着即使接收信噪比不变时,HASD的检测概率仍随目标方位起伏,影响检测过程中的稳健性. 为了使HASD 的检测概率不随目标方位起伏,从而获得稳健的检测性能,需要构造维数恒定的角度域子空间.观察(12)式,参数集的值域宽度 |(kmax−kmin)sinθs| 随θs变化,导致K(θs)随之变化.构造区间 [∆1,∆2],通过平移量δθs将参数集平移至该确定区间中,对应的矩阵变换关系将使变换到区间 [∆1,∆2] 对应的空间中.区间 [∆1,∆2] 对应的空间是一个固定的空间,那么通过矩阵间线性关系即可得到所求维数恒定的角度域子空间. 得到N ×Z维矩阵 此时 类比(14)式,将矩阵F近似表示为 式中,ΛF,UF和VF分别表示有效秩KF对应的奇异值矩阵和奇异向量矩阵.将(37)式、(36)式和(13)式代入(10)式可得: 本节通过仿真实验,结合角度域子空间有效性和维数变化,仿真分析了HASD 和RHASD 的平均检测能力、不确定环境中的稳健性、随θs的起伏特性,给出了先验信息失配时RHASD 的性能变化,并将RHASD 与不确定环境中的3 种宽容检测器——蒙特卡罗优化广义似然比检测器(Monte Carlo-generalized likelihood ratio detector,MCGLRD)、子空间检测器(subspace detector,SD)、能量检测器(energy detector,ED)进行比较.仿真实验中不确定浅海环境如图2 所示,各参数不确定范围如表1 所列.目标声源发射300 Hz 单频信号,接收阵为固定布放在海底的100 元HLA,阵元间隔2.5 m.由于本文研究的是低频浅海中的远场问题,因此仿真过程中不同环境条件下模态函数和水平波数由KRAKEN 软件进行计算,具体声场均由(1)式计算获得. 在表 1 所列不同海洋环境参数的取值范围中采样1000 次,得到1000 个不同的环境参数实现.在1000 个环境参数条件下,可远场传播的模态数如图 3(a)所示,可以看出,目标激发出的可远场传播的模态数是不同的,这意味着HLA 能采样到的行波信息也是不同的.已知海底声速和沉积层上表面声速的不确定范围时,可以得到海底声速的最小值 min{cb}=1477.5 m/s,沉积层上表面的最大值max{cd}=1650 m/s.此时,估计角度域子空间所需的两个波数值kmin=1.14,kmax=1.28 .图 3(a)中各模态对应的水平波数值均在k1和k2之间,如图 3(b)所示.在 (k1,k2) 内等间隔采样,采样间隔为0.001,按照(12)式、(14)式和(17)式,选取ν2=0.9995,得到不同θs对应的角度域子空间给定∆1=(kmin−kmax)/2,∆2=(kmax−kmin)/2,δs=−(kmin+kmax)/2,按照(35)式、(37)式和(39)式可以得到稳健角度域子空间的维数如图4 所示,图中理想的角度域子空间W(θs) 由1000 个环境参数对应的观测矩阵构造,其维数同样由有效秩估计.由图4 可以看出,和W(θs) 的维数成阶梯式变化,在θs=0◦时最小,在θs=±90◦时最大,的维数略小于W(θs) 的维数.而的维数在各θs相同,等于W(θs) 的最大维数. 图3 1000 个环境参数实现下传播模态的水平波数(a)传播模态阶数;(b)水平波数Fig.3.Horizontal wave numbers of propagating modes in 1000 environmental realizations:(a) Numbers of propagating modes;(b) wave numbers. 图4 不同水平方位角对应的角度域子空间维数Fig.4.Subspace dimensions of angle-domain corresponding to different horizontal azimuth angles. 图5 角度域子空间在不同空间位置处的有效性 (a) ;(b)Fig.5.Validity of angle-domain subspaces at different spatial positions:(a) (θs) ;(b) 考虑图2 所示不确定环境中的两个实现,具体参数如表 2 所列.在这两个环境实现中,目标激发的可远场传播模态数分别为12 和18,对应的水平波数如图 6(a)所示.显然,由于环境1 对应的沉积层上表面声速接近表 1 中不确定范围的最小值,而环境2 对应的沉积层上表面声速接近不确定范围的最大值,故环境1 中传播模态的数目较环境2 中少.当目标深度zs=50 m,水平距离rs=6000 m,水平方位角θs=40◦时,HLA 采样到的各阶模态行波的归一化幅度由图 6(b)给出.因为环境1 中激发的传播模态数少,所以HLA 在环境1 中采样到的行波信息更少. 图6 两个环境实现下的水平波数和HLA 接收到的归一化行波幅度 (a)水平波数;(b)归一化行波幅度Fig.6.The horizontal wave numbers and the amplitude of the normalized traveling wave received by HLA in two realizations:(a) Horizontal wave numbers;(b) normalized traveling wave received. 表2 不确定浅海波导中的两个环境实现Table 2.Two realizations of the uncertain shallow waveguide. 在两个环境实现中,将HLA 接收信号s投影到不同θ对应的角度域子空间中,得到 RSL(θ) 曲线如图7 所示.由图7(a)可以看出,两条 RSL(θ) 曲线近似相同,且均在θ=θs处近似为0,对应信号能量损失可忽略不计.这一现象表明,尽管在两个环境中HLA 接收到的信息不同,角度域子空间均可以利用到近似全部的信号能量.结合第3.1 节可知,由于信号能量损失可忽略且RSL(θ)曲线近似,这两个环境实现下HASD 应具有接近的检测性能,此时HASD 检测概率只与阵列信噪比有关.HASD 在两个环境中的检测概率如图8(a)所示,图中 SNR 为阵列信噪比的分贝形式,虚警概率Pf=0.1,每个 SNR 点上的检测概率Pd由10000 次独立试验计算获得.可以看出,HASD 在各 SNR 点上的检测概率在两个环境实现下近似,检测概率仅有0.2 的差异.图7(b)和图7(a)类似,角度域子空间中同样可以利用到近似全部的信号能量,对应两个环境实现下的RHASD 检测性能同样只与阵列信噪比有关.如图8(b)所示,RHASD 的检测概率差异不足0.01. 图7 两个环境实现下的 RSL(θ) 曲线 (a) ;(b)Fig.7.RSL(θ) in two realizations:(a) ;(b) . 图8 两个环境参数实现下HASD 和RHASD 的检测性能 (a) HASD;(b) RHASDFig.8.Detection performances of HASD and RHASD in two realizations:(a) HASD;(b) RHASD. 为了进一步验证HASD 和RHASD 的检测性能在不确定环境中具有稳健性,给出1000 个不同环境实现下HASD 和RHASD 的检测概率,如图9所示.在图9(a)中,HASD 在1000 个环境参数条件下的Pd-SNR 曲线均在平均曲线的附近,对于相同检测概率,HASD 所需 SNR 起伏约为1 dB;在相同 SNR 下,检测概率起伏约为0.1.RHASD 的检测概率如图9(b)所示,对于固定检测概率,HASD所需 SNR 起伏约为0.4 dB;在相同SNR 下,检测概率起伏约为0.05.根据前文分析可知,由于和能包含不同环境条件下HLA 采集到的信息,故HASD 和RHASD 在不确定环境中均具有一定的稳健性,其中RHASD 的稳健性略高于HASD. 图9 1000 个环境参数实现下HASD 和RHASD 的检测性能 (a) HASD;(b) RHASDFig.9.Detection performances of HASD and RHASD in 1000 realizations:(a) HASD;(b) RHASD. 假设环境参数为表 2 中所列的环境1,目标的深度和距离仍为zs=50 m 和rs=6000 m,目标的水平方位角θs分别为 40◦和 10◦.此时,s投影至角度域子空间中,得到 RSL(θ) 曲线如图10所示.图10(a)中,两条曲线在各自θs处达到最小值,此时θs=40◦的邻域范围C1(θs)=[39◦,46◦],结合图4可知,在C1(θs) 范围内的维数为6,而θs=10◦的邻域范围C1(θs)=[10◦,11◦],对应维数为3 和4.根据3.1 节分析可知,目标位于θs=10◦时HASD 的检测概率会小于目标位于θs=40◦时对应的HASD 的检测概率.给出HASD 在不同SNR时HASD 的检测概率如图11(a)所示,在SNR=0—15dB 条件下,θs=40◦时HASD 的检测概率均大于θs=10◦时的检测概率.而在图10(b)中,θs=40◦的邻域范围C1(θs)=[38◦,47◦],θs=10◦的邻域范围C1(θs)=[7◦,14◦],由 于的维数恒定,故这两个邻域对应维数均为8.此时RHASD 的检测概率如图 11(b)所示,目标在不同方位上时RHASD 具有近似的检测概率.由上文分析可知,受角度域子空间维数变化的影响,HASD 的检测概率随目标方位起伏,而RHASD利用了维数恒定的角度域子空间,其检测概率不随目标方位起伏. 图10 目标分别位于 40◦ 和 10◦ 的 RSL(θ) 曲线 (a) (θ) ;(b)R(θ)Fig.10.RSL(θ) when the source bearing are at 40◦ and 10◦ :(a) (θ) ;(b) R(θ) . 图11 目标分别位于 40◦ 和 10◦ 时HASD 和RHASD 的检测性能 (a) HASD;(b) RHASDFig.11.Detection performances of HASD and RHASD when the source bearing are at 40◦ and 10◦ :(a) HASD;(b) RHASD. 为了进一步比较HASD 和RHASD 在目标位置变化和环境参数变化时的检测性能,随机选取1000 个不同的目标位置,结合1000 个不同环境参数实现,构成了1000 个检测过程.其中,为了保证HASD 和RHASD 的适用性,需要满足目标位置在的有效范围内,结合图5,设目标深度、水平距离、水平方位角在 1—100 m,5—20km,−90◦—90◦范围内.这1000 个检测过程中,HASD 和RHASD 的平均检测性能如图12(a)所示,在不同目标位置和环境参数条件下,HASD和RHASD 具有接近相同的检测概率.这1000 个检测过程对应的不同Pd-SNR 曲线,如图12(b)所示,HASD 在相同检测概率条件下,对 SNR 的需求差异在4 dB 以上,而RHASD 仅为0.5 dB,即RHASD显著地提高了HASD 的稳健性.在 SNR=11 dB时,给出两种检测器的检测概率随θs的变化,如图12(c)所示.图12(c)中,θs由±90◦到 0◦时,HASD检测概率下降,而在相同θs上检测概率近似相同,表明HASD 的检测概率随θs明显起伏,而受环境参数、目标深度距离变化的影响不大.而RHASD在1000 个检测过程中检测概率近似相同,其最低检测概率比HASD 的最低检测概率高达0.51.结合图12 中3 个图示可知,RHASD 具有和HASD近似相同的平均检测概率,同时稳健性远高于HASD. 图12 不同目标位置和环境参数条件下HASD 和RHASD的检测性能 (a)平均检测性能;(b)各参数条件下检测性能;(c)检测概率随目标方位起伏Fig.12.Detection performances of HASD and RHASD in different environments and source positions:(a) Average detection performance;(b) detection performance in different realizations;(c) detection probability fluctuates with the target bearing. 由于RHAD 具有和HASD 近似相同的平均性能,同时较HASD 更为稳健,故将RHASD 作为本文最终得到的稳健检测器,与常用宽容检测方法,即MC-GLRD,SD,ED 进行比较.为了更好地比较在同样条件下的检测性能,仿真中设MCGLRD 的参数搜索数为1000,以达到和RHASD接近的计算量.SD 方法所需的信号特征子空间由1000 个环境参数对应的信号波前矩阵估计. 随机选取1000 个不同的目标位置,结合1000个不同环境参数实现,构成了1000 个检测过程.4 种检测器的平均检测概率如图13 所示.由于ED 没有利用任何先验信息,在各信噪比条件下平均检测概率是4 种检测器中最低的.MC-GLRD利用了所有参数的不确定范围,在各信噪比条件下具有最高的平均检测概率.SD 与MC-GLRD 利用的先验信息相同,但由于HLA 的信号特征子空间维数此时为100,退化为能量检测器,故各信噪比条件下平均检测概率与ED 一致.本文提出的RHASD 只利用了海水中的海底声速和沉积层上表面声速的不确定范围,在各信噪比条件下平均检测高于SD 和ED,相同信噪比条件下信噪比要求低于SD 达2 dB,高于MC-GLRD 约0.5 dB.选取 SNR=11 dB,给出1000 次实现下的4 个方法的检测概率如图13(b)所示.在接近的计算量条件下,MC-GLRD 由于其本身的特性,会出现检测概率明显下降的情况,稳健性较低.RHASD 的检测概率在各参数条件下近似一致,具有与SD 和ED相近的稳健性,同时比SD 检测概率高约0.3.综上所示,RHASD 在不确定环境中具有较高的平均检测性能,同时还具有较高的稳健性. 图13 RHASD 与MC-GLRD,SD,ED 性 能对比 (a)平均检测性能;(b)不同实现下的检测概率Fig.13.Detection performances of HASD,MC-GLRD,SD,ED:(a) Average detection performance;(b) detection probability in different realizations. 本文定义了不确定环境中的角度域子空间并给出了一个先验信息要求少、计算复杂度低的估计方法,提出了角度域子空间检测器HASD.在此基础上,构造了维数恒定的角度域子空间并得到了HASD 的稳健形式RHASD. 通过仿真实验分析了角度域子空间的有效性和HASD 和RHASD 在不同环境参数和目标位置处的检测性能,结果表明:1)角度域子空间在远场有效性高,故HASD 和RHASD 适用于远场条件;2) HASD 和RHASD 在不确定环境参数中具有一定的稳健性;3) HASD 的检测性能随目标方位的变化而起伏;4) RHASD 与HASD 平均检测性能近似一致,同时改善了HASD 性能随目标方位起伏的问题.将RHASD 和常用的宽容检测器进行仿真对比,仿真结果表明RHASD 平均检测能力略低于MC-GLRD,但平均性能远高于SD 方法和ED方法;其稳健性与ED 近似,高于MC-GLRD 方法.







2.3 有效性量度

3 HLA 角度域子空间检测方法及其稳健改进形式
3.1 HLA 角度域子空间检测方法
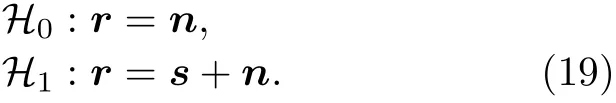


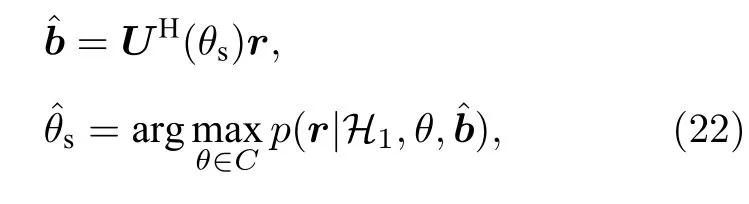

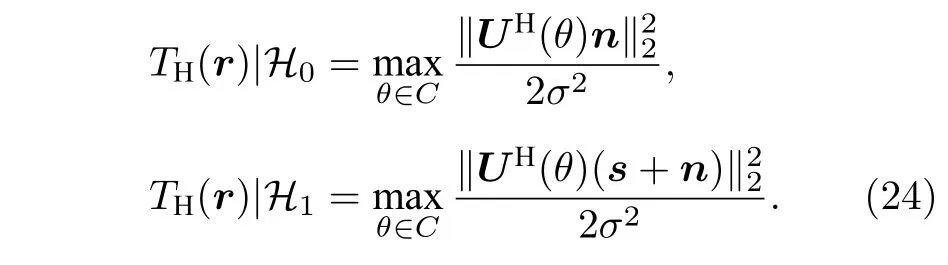
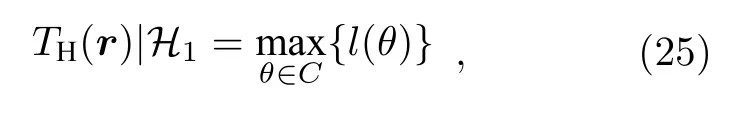

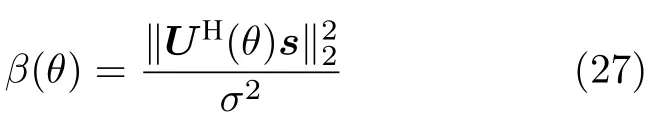

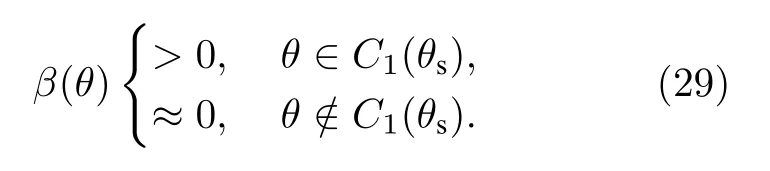


3.2 稳健改进形式






4 仿真与讨论
4.1 角度域子空间有效性分析


4.2 HASD 和RHASD 在不确定环境中的稳健性


4.3 HASD 和RHASD 检测性能随目标方位起伏特性分析

4.4 RHASD 与MC-GLRD,SD,ED 性能比较
5 结论

