纳米尺度热物理中的声子弱耦合问题

潘东楷 宗志成2) 杨诺†

1) (华中科技大学能源与动力工程学院,武汉 430074)

2) (中国石油大学(华东)新能源学院,青岛 266580)

纳米尺度热物理中的诸多新现象、新机制与声子弱耦合存在密切关联.本文介绍了声子弱耦合机制,以及相关的物理现象:低维体系中热导率的尺寸效应、声子双温度现象和范德瓦耳斯堆叠界面的高热阻等.同时概述了近年国内外学者对于这些新颖物理现象的前沿研究成果.对声子弱耦合目前面临的问题,例如理论模型如何加入声子波动性等,进行了简要讨论和展望.

1 引言

随着21 世纪初人类工业进入纳米时代,以芯片为代表的工业器件功率密度急剧增加,散热瓶颈成为制约其发展的主要因素.从科学的角度,微纳尺度热传导具有区别于宏观的新现象、新理论和新方法的特点.因此微纳尺度热管理成为科学家和工业界都关心的问题[1−5].在芯片等器件的散热中,普遍思路是利用本征热导率高的材料或高导热界面材料来帮助散热[6,7].这类材料更多的是非金属低电导材料,其中的主要热载流子是声子.因此,对声子输运的机理研究不仅能加深科学的认知,而且有助于改善微纳尺度器件的热管理.

20 世纪中叶,玻恩和黄昆合著的《晶格动力学》,以格波量子(声子)的形式系统地对宏观体块晶体结构中的热能输运进行解释,为其提供理论基础.宏观体系中的声子输运,往往被看作准粒子输运,从而服从玻尔兹曼输运方程.但在微观体系,声子的波动性表现得也越来越明显[8].此外,在宏观体块结构中,声子之间相互作用比较强、声子散射也比较充分,对热输运造成阻碍.与之形成鲜明对比的是在低维纳米体系中,出现的声子弱耦合,即纳米体系中声子间相互作用远弱于宏观体系的情况[9−14].而这方面的输运研究十分匮乏、迫切需要新理论和新方法.

目前弱耦合主要发生在低维纳米体系和范德瓦耳斯堆叠界面等情况中.弱耦合机制对于声子输运的影响也是多方面的:一方面弱耦合会减少体系内的声子散射,从而利于提高热传导、获得较高本征热导率[9,10];另一方面弱耦合也是阻碍纳米堆叠界面热传导的重要因素之一[15,16].如图1 所示,目前在研究中发现的许多新现象、新机制都与声子弱耦合相关联,比如热导率尺寸效应[17,18],声子双温度现象[10,19],梯度热导率现象[20,21]和双通道热输运现象[22,23]等,后文将对这些现象以及其与弱耦合的关系进行介绍.

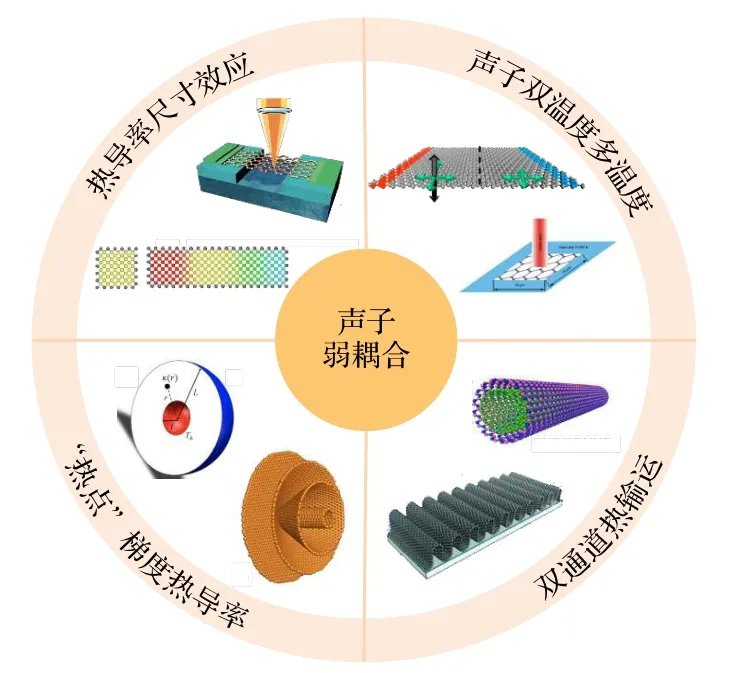
图1 与声子弱耦合紧密相关的多个低维纳米尺度导热的新物理现象[10,17−23]Fig.1.The new physical phenomena in low dimensional heat conduction closely related to the phonon weak couplings[10,17−23].

2 纳米体系内弱耦合

低维纳米体系的热导率会呈现出尺寸效应,即热导率的数值会随着体系尺寸的变化而变化.这种非傅里叶现象,很可能和体系中的声子弱耦合息息相关.一方面,和宏观体块材料相比,低维纳米体系原子总数(N)通常会明显减少.因此,体系中的声子本征模式总数(3N)也显著减少.从而不同模式之间的相互作用和耦合就会变弱.另一方面,声子之间的散射也会大幅减少.多声子散射时需要服从能量守恒和准动量守恒定律,由于低维体系在不同维度方向上具有明显的各向异性,模式与模式间的差异非常大,因此对比三维宏观体系,低维纳米体系中的声子耦合会受到抑制,从而声子具有更长的平均自由程,这会对声子的输运造成显著影响.

低维纳米体系中声子较长的平均自由程会导致其更容易受到体系尺寸的限制,当体系尺寸小于平均自由程时,声子输运主要受到边界散射的影响,产生尺寸效应.尺寸效应主要表现为热导率随着尺寸的增大而持续增大.从20 世纪末至21 世纪初这方面的研究开始不断涌现,起初集中在一维和二维原子链模型的研究,并得到了热导率持续增大不收敛的结果[24−30]以及不同于经典热扩散规律的现象[31−37],从而引起人们对低维体系尺寸效应研究的兴趣.

之后,在准一维纳米体系(纳米线、纳米管等)中也发现了热导率的尺寸效应[38−41].对硅纳米线的理论和模拟研究都发现其热导率随长度的增加而呈现幂指数(power law)持续增大[40,41].近期通过对NbSe3纳米线的测量,实验得到与模拟结果相吻合的增大趋势[42].在碳纳米管和石墨烯纳米带的模拟研究中,也发现了热导率随着长度呈现出幂指数增大[38,43−46].之后的实验测量也观测到模拟中预测的热导率对尺寸依赖的结果[47,48].

对二维材料热导率的研究中也存在尺寸依赖效应[27,30,49].石墨烯,第一个被制备的二维材料,因为具有极高热导率(比金属热导率还高一个量级)而成为导热领域的研究热点[50].由于石墨烯的二维对称性,导致面外声子(outplane phonons)与其他声子的相互作用受到限制,因此面外声子的散射率降低、自由程增长[14,51,52],这也意味着其具有较高的导热能力.然而关于ZA 支声子(平面外的声学声子)的热导率贡献目前尚存争议.Nika 等[53]提出以ZA 支声子为代表的长波声子具有极高的热导率贡献.Bonini 等[54]也通过数值计算得出ZA支声子对石墨烯热导率贡献最大.但Feng 等[55,56]后续通过考虑四声子的模拟计算并发现石墨烯中ZA 支为代表的长波声子对热导率的贡献并不高.此外,在尺寸与自由程可比时,边界散射明显影响声子输运,从而会出现尺寸效应[53].Xu 等[57]在实验测量中观测到石墨烯的面内热导率随着尺寸的增大呈现出不收敛的增加趋势.Li 等[58]在MoS2的数值模拟中也发现了其热导率的尺寸效应.而Zhu 等[59]发现在单层磷烯的不同方向上热导率呈现出对尺寸的不同依赖性.

上述结果明显与经典的傅里叶定律描述的热导率—一个不依赖于系统尺寸的物理量—相违背[60].此外,也有模拟研究认为当足够长时,石墨烯和纳米管的热导率最终会收敛到特定值而不是随尺寸的增大不断增大[61−64].总之,目前对于低维体系的研究都明确说明当尺寸小于声子自由程时,热导率会有明显尺寸依赖特性,并呈现持续增大的趋势.当尺寸远大于自由程时,热导率是继续增大还是收敛,仍然是一个开放的问题,值得继续讨论和研究.

单一纳米体系内部的声子弱耦合还会带来其他新颖的现象,例如声子多温度现象[10,19,65]和梯度热导率[20,21,66].同时由于体系内不同声子分支之间的散射强度不同,会出现不同声子分支之间的弱耦合,导致部分声子的散射率明显降低,这极大地有利于热输运的增强.

以石墨烯为例,由于受到对称性的影响,ZA支声子散射受到明显抑制[52],因此导致相应的ZA 支声子普遍具有较大的自由程,其中低频区的声子更为明显,也就出现了弱耦合的现象.An 等[10]提出用双温度模型来处理不同声子群之间的耦合,在双温度模型中弱耦合的两个体系可以拥有不同的“温度”,这一点也在数值模拟中得到了验证.

近年来,我们和合作伙伴也关注到了纳米“热点”的热输运问题.在纳米石墨烯圆盘及碳纳米锥等结构中,发现了“热点”的梯度热导率现象[21,66].使用隐式离散坐标法求解玻尔兹曼输运方程[67,68],将“热点”问题的研究拓展到微米尺度的二维和三维结构,同样发现了其中的梯度热导率现象[20].“热点”周围的梯度热导率与声子弱耦合存在密切关系,当体系内声子间的耦合作用增强时,梯度热导率现象逐渐减弱直至消失.

3 纳米体系间弱耦合

声子弱耦合机制还会影响在两个或多个纳米体系之间的热输运,例如范德瓦耳斯堆叠界面(vdw cross-interfaces)[69,70]、一维纳米套管[71,22]等.体系间一般通过较弱的力场(例如范德瓦耳斯力等)相互作用,因此体系间声子的耦合要远弱于体系内的声子耦合,声子的弱耦合在这些体系中也扮演了重要角色.

范德瓦耳斯堆叠界面指的是两个堆叠的低维结构之间形成的界面,与传统界面不同,范德瓦耳斯堆叠界面处的导热不只是界面法线方向的一维导热,也包括界面单侧的低维结构内部的导热,因此范德瓦耳斯堆叠界面的导热是一个二维导热过程[72−75].例如两个堆叠的纳米带,在堆叠界面处的相互作用通常为范德瓦耳斯力,它远弱于纳米带内原子间的共价键.再加上界面两侧的不同种类纳米带的声子本征模式分布存在差异,这些都会阻碍界面处的声子输运.Feng 等[76]也通过基于弱耦合的方式对界面热传导建立了有效模型,展示了弱耦合在界面热传导中的影响,也通过该模型解释了实验测量CuPc 堆叠界面的高热阻[9,77].此后Deng 等[9]提出了对于范德瓦耳斯堆叠界面的完整弱耦合数学模型.

折叠二维材料(如折叠石墨烯)以及多层二维材料由于内部存在诸多范德瓦耳斯堆叠界面,也会受弱耦合机制的影响.折叠石墨烯因为在磁场下表现出特殊的电性质而得到关注[78−82].同时折叠也是一种非常新颖独特、有效调控低频长波声子的调控机制,它与调控高频声子的诸多传统方式有很大不同.通过对折叠石墨烯的模拟研究,发现其中的弱耦合机制影响着折叠对体系的热调控效果[23,83].在多层二维材料的研究中也发现,无论是层间夹角还是张力都会对结构的声子输运性质以及相关的热、电性质造成显著的调控效果[84,85],这也显示了声子弱耦合对于多层二维材料性质的影响.而一维纳米套管的不同直径纳米管之间由于范德瓦耳斯力的相互作用,也会产生声子弱耦合.在对一维纳米套管的研究中发现套管间相互作用的强弱会对声子的输运造成明显影响[22,86],当套管间相互作用强度远超范德瓦耳斯力时,弱耦合变为更强的耦合作用,热导率会明显下降,说明声子输运受到阻碍.这也验证了声子弱耦合对于声子输运的重要影响.

4 总结和展望

综上所述,声子弱耦合作为微纳体系中观测到的新物理现象,在基础研究和电子、光电、热电等[87−90]工业应用领域都展示出不可忽视的作用和研究价值.

一方面,一些低维纳米体系——比如石墨烯和六方氮化硼等——内部存在声子弱耦合机制.这些系统具有优异的导热特性,作为这些特性的重要影响因素,对弱耦合机制进行深入研究有利于对低维纳米体系的进一步理解和探索.但是目前对于低维纳米体系声子输运的研究更多的是实验测量和模拟计算结果,缺乏普遍接受的理论解析结果.

另一方面,纳米体系间的弱耦合源于结构特性,例如一维套管和二维折叠等结构内会形成大量的范德瓦耳斯堆叠界面.体系间的弱耦合也会为声子输运带来影响或提供调控.这些堆叠界面处的声子输运可以借助我们提出的声子弱耦合模型来理解和描述.然而声子弱耦合模型[9]是建立在玻尔兹曼输运方程基础上的,也就意味着该模型仅适用于粒子输运情况.随着体系变小,纳米结构内的声子输运波动性越来越强[8].因此,更精确的描述需要建立包含波动性输运的声子弱耦合模型,这有待进一步研究.

此外,当基础研究向应用研究推进时,会遇到跨尺度问题.跨尺度问题在研究方法上也面临挑战.因为缺少适应多个尺度的统一方法,不同的方法都有各自的假设和适用范围,例如:密度泛函的绝热近似,分子动力学的经典分布,晶格动力学的零温假设和周期性边界条件,玻尔兹曼输运方程的粒子性前提等.现在通常简单地使用两种或多种方法联合模拟,即先在微观尺度独立模拟计算,再将结果传递到宏观尺度的模拟中进行计算.但这样的方式存在明显问题,简单的使用两种或多种方法联合模拟会带来适用性问题,不同方法的假设之间会相互干扰甚至冲突,降低最终结果的可靠性.此外,一些重要的实际体系无法使用联合模拟方法进行研究,例如纳米结构的体块材料、纳米复合材料等.

目前从声子弱耦合角度开展的研究工作偏少,相应的探索还处于初步阶段.希望通过本文的探讨,引起更多学者的兴趣和关注.