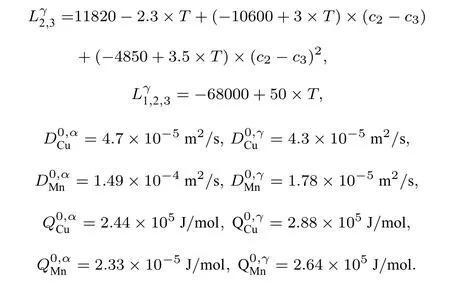相场法研究Fe84Cu15Mn1 合金富Cu 相析出的内磁能作用机理*

蒋新安 赵宇宏 杨文奎 田晓林 侯华

(中北大学材料科学与工程学院,太原 030051)

本文基于连续相场模型,对内磁能作用下Fe-Cu-Mn 合金中富Cu 相析出行为进行了研究,得到不同温度、不同Mn,Cu 含量条件下的内磁能对富Cu 相的平均颗粒半径、体积分数、吉布斯自由能的影响.模拟结果表明,Mn 含量越低,居里温度越高,内磁能对自由能的贡献越大,且内磁能的贡献随温度升高而减小;内磁能降低了相结构转变势垒,促进了相结构转变.沉淀相体积分数随Cu 含量增加而增加,通过对比有无内磁能对沉淀相体积分数的影响,内磁能作用导致沉淀相拥有更大的体积分数.因此在内磁能作用下,富Cu 相具有较大的平均粒径、体积分数和较小的矫顽力,同时预测了合金硬度的变化趋势.

1 引言

反应堆压力容器(reactor pressure vessel,RPV)作为核电站的核心设备,其安全使用年限决定了核电站的寿命[1],有研究表明时效或辐射诱导Cu/Mn/Ni 沉淀会导致RPV 钢硬化造成脆裂[2−4],将严重影响核电站的安全使用寿命.一般外界因素如辐照或弹性效应往往掩盖了磁能对沉淀析出的贡献[5−9].但是,Gorbatov 等[10,11]研究发现,铁的磁性状态在Fe-Cu 合金的分解中起着至关重要的作用,并且为了正确地对Fe-Cu-X 合金中的析出现象进行理论上的描述与分析,应正确考虑磁性及其与温度有关的贡献,并从基于密度泛函理论的第一性原理有效对相互作用(effective pair interactions,EPI)统计热力学模型研究了Fe-Cu-X(X=Ni,Mn)合金体系中的分解,结果表明EPI 表现出对磁性的强烈依赖性,影响不同温度下的相分离.文献[12]指出吉布斯自由能(Gibbs free energy,GFE)作为沉淀析出的主要驱动力可以表示为磁性贡献和非磁性贡献的叠加.

磁性作为材料的物理性能,实验手段无法将材料的物理性质脱离材料本体进行单独研究.但是,以热力学和动力学为基础的相场法能够定量描述固态相变过程中组织及结构、化学、热力学参数随时间的演化过程[13−20].因此,采用相场法可以定量的从微观角度模拟、预测 RPV 钢中富Cu 相的沉淀演化过程.

Wang 等[21]研究指出,剩磁(remanence)Br和饱和磁感应强度(saturation magnetic induction)Bs的一致变化反映了材料磁化强度的整体变化,磁性的变化往往会导致内部磁场发生变化.内磁能(internal magnetic energy,IME)即内部磁场变化所产生的能量,本工作将IME 耦合到自由能项中,分别研究了不同温度、不同Mn,Cu 含量条件下的IME 对富Cu 相的平均颗粒半径、体积分数、吉布斯自由能的影响.本文研究IME 对Fe-Cu-Mn合金富Cu 沉淀过程的演化机理,将对RPV 钢的合金设计和沉淀相析出机理有重要指导意义.

2 相场模型

对于Fe-Cu(原子含量为15%)-Mn(原子含量为1%)三元合金沉淀演化,引入3 个浓度场ci(r,t)(其中i=1,2,3 分别代表Fe,Cu,Mn)和一个结构序参数η(r,t),这些场的时间以及微观结构演化是通过Cahn-Hilliard (C-H)方程和Allen-Cahn (A-C)方程[22,23]的数值解获得:

其中,ξc(r,t)和ξη(r,t) 是随机热波动项,以促进相分离的发生;Mi(i=Cu,Mn) 是合金成分的化学迁移率;L是表征相变演化的动力学迁移率.Mi与组成元素的原子迁移率有关[24−26]:

其中,c0i表示合金元素的标称成分i,分别表示α(BCC)和γ(FCC)相的原子迁移率[27−29]:

其中,R为气体常数,T为绝对温度,扩散系数可分为频率因子和扩散激活能,可以写为[30,31](具体参数见附录A)

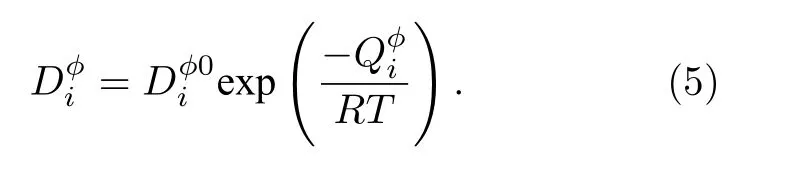
2.1 系统总自由能

为了定量模拟微观结构变化,需要精确计算微观结构的总自由能泛函[32],非均匀系统的总自由能F为[33]

式中,G(ci(r,t),T) 代表系统的体积自由能,ci(r,t)表示在空间位置r和时间t下成分i的局部成分场,两项中kc和kη分别为成分梯度能系数以及序参数梯度能系数.

系统的体积自由能可以表示为

其中,函数h(η) 被定义为h(η)=η2(3−2η)[34,35],是0—1 之间的单调函数;Gα(ci,T)和Gγ(ci,T) 为ci和T的函数分别表示α相和γ相的吉布斯自由能;Wg2(η)表示BCC 相和FCC 相之间的相变能垒,W是双势阱的高度,通常取一个很大的正数,g(η)=η(1−η).

用亚正则溶液近似描述了Fe-Cu-Mn 三元合金体系中相的化学自由能[36],本模拟所使用的吉布斯自由能函数Gϕ(ci,T)(ϕ=α,γ) 为

由(3)式可知,吉布斯自由能包括以下几项:纯元素的GFE、混合GFE、过剩GFE 和磁能.当前,大部分研究在用相场法计算合金的自由能时,为了简化处理都不考虑IME 的影响[6,7,38−40].但是IME 对合金中析出相也会有影响,尤其对于含有铁磁性元素Fe,Mn 的合金非常有必要研究.

Gmg,ϕ是内磁能对GFE 的贡献,可以表示为

3 模拟结果与分析

在给定的热力学条件下,亚稳相将转化为具有最小吉布斯自由能的稳定相[41],图1 所示为不同温度条件下,有无IME 作用GFE 随Cu 含量的变化情况.可以发现,无论有无IME 作用的影响,GFE 随Cu 含量增大都会呈现出先升高再降低的变化趋势,文献[42] 指出Cu 颗粒的沉淀过程可以看作伪失稳分解,富Cu 析出相除了早期Cu 元素的积累外,还经历了BCC-FCC 的相结构转变,符合伪失稳分解的特征:1) 物质的一种或多种组分通过扩散过程重新分布,形成富集区和枯竭区;2)富集或枯竭区域发生结构转变,产生与母相(即基质)不同的晶格结构的新相.如图1(a)所示,不考虑IME 作用影响时,无论温度高低,FCC 结构相的GFE 总是低于BCC 结构相,说明此时的沉淀相总是具有最小GFE 的稳定FCC 相,这与相图结果不符[43,44].因此,又考虑了IME 对双相GFE 的影响,如图1(b)所示.在IME 作用影响下两相自由能存在交点,当Cu 含量分别小于0.72,0.69,0.62,0.49 时,BCC 固溶体GFE 要明显小于FCC 固溶体,并且BCC 相结构要比FCC 更稳定;当Cu含量分别大于上述浓度值时,FCC 结构相能量要小于BCC,这说明在此实验温度条件下,随着Cu 浓度升高,BCC 结构逐渐向FCC 结构发生转变;同时由高温到低温对比了4 组不同温度条件下的曲线,临界点有明显左移现象,说明相结构转变对温度的变化存在依赖性.在温度为823 K 时,FCC 向BCC 转变的Cu 含量临界值为0.69,从理论上讲,当体系某点的Cu 浓度超过0.69 时就已经发生了由BCC 向FCC 的转变,与伪失稳分解的特征相吻合,并且随着Cu 含量的增加,FCC 结构的能量会更低,形成稳定的FCC 沉淀相,这种现象在文献[45]中也被证实过.由此可见,IME 对体系自由能和相结构转变的贡献不可忽略.

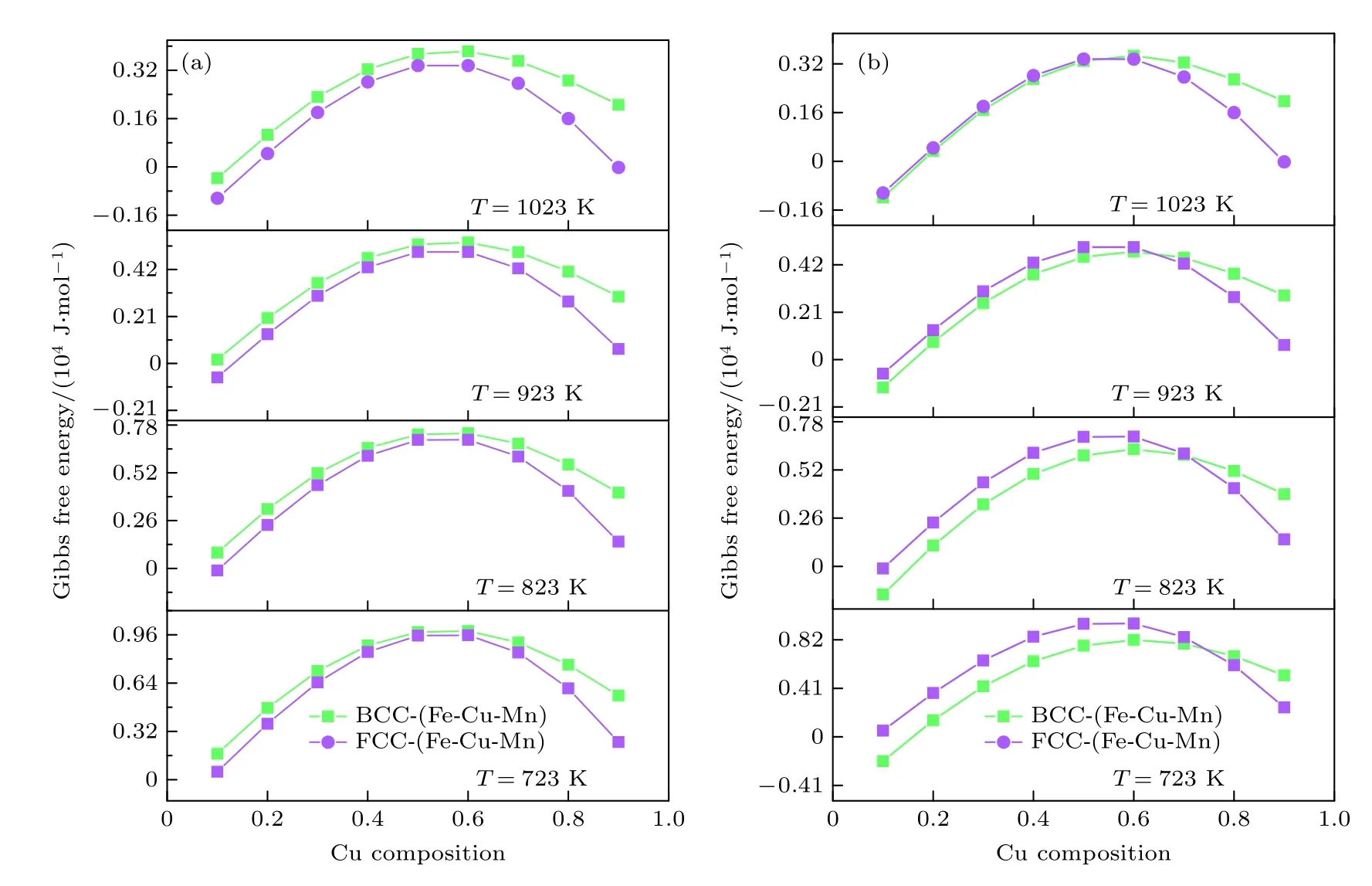
图1 不同温度下GFE 随Cu 浓度变化情况 (a) 不考虑IME 作用;(b) 考虑IME 作用Fig.1.Gibbs free energy versus Cu concentration at different temperatures:(a) The effect of internal magnetic energy is not considered;(b) the effect of internal magnetic energy is considered.

IME 不仅影响相结构转变的GFE,还对沉淀相长大阶段形貌有影响.图2(a)—(f),(j),(k)分别为无IME、有IME 作用下的沉淀演化过程以及晶粒尺寸对应不同时间步数的曲线.时效初期(t∗<7500),Cu 原子随机分布在Fe 基体中,随着演化的进行,溶质的过饱和为成核和结晶提供了化学驱动力,Cu 原子聚集形核,并以吸收基体中Cu 原子的方式不断析出.富Cu 相不断长大并达到稳定的晶粒尺寸.如图2 所示,相同时间步数下,无IME 作用下的成分起伏点更多,并且优先析出沉淀相(如图2(b)红色标注).当析出相长大到一定尺寸时,有IME 作用下才出现个别沉淀相(如图2(c),(h)黄色标注).当无IME 作用下的沉淀相数量和尺寸趋于稳定时,有IME 下的沉淀相还处于长大阶段.对比可以发现IME 对沉淀相的形核演化过程有一定的阻碍作用.图2(k)为演化过程中的颗粒半径变化图,其中No-IME 表示没有IME 作用,With-INE 表示有IME 作用,斜率大小代表了尺寸变化率的大小.对比两个状态下的平均颗粒半径,IME作用下的平均半径大于无磁能作用下的平均颗粒尺寸.并且在长大阶段,无IME 状态下尺寸变化率更高.当沉淀相的平均半径达到2.69 nm 时,尺寸变化率又趋于平缓,有IME 作用下的平均颗粒半径以稳定的变化率呈线性增长,达到稳定时尺寸将不再变化.说明IME 对颗粒的长大过程和颗粒尺寸也有较大的影响,并且在IME 的影响下颗粒长大过程更加平稳.

图2 (a)—(e) 823 K 时无IME 作用下的演化过程 (a) t∗=7500,(b) t∗=8500,(c) t∗=9000,(d) t∗=9500,(e) t∗=11000;(f)—(j) 有IME 作用下的演化过程 (f) t∗=7500,(g) t∗=8500,(h) t∗=9000,(i) t∗=9500,(j) t∗=11000;(k) 有IME 与 无IME 作用下的平均颗粒半径变化Fig.2.(a)–(e) The evolution process without internal magnetism at 823 K:(a) t∗=7500,(b) t∗=8500,(c) t∗=9000,(d) t∗=9500,(e) t∗=11000;(f)–(j) the evolution process with internal magnetism:(f) t∗=7500,(g) t∗=8500,(h) t∗=9000,(i) t∗=9500,(j) t∗=11000;(k) the change of average particle radius with and without internal magnetism.

合金元素取代Fe 原子会导致局部磁态以及晶体结构的转变[46],而作为顺磁性元素Mn 还会加速沉淀动力学[11,47,48].由于Cu 在Fe 中的溶解度不高,并在Fe 基体中快速扩散[49],因此最初富含Cu 的沉淀相,通常与Mn 形成合金.并且最初Mn偏析导致界面能的降低,因此会迅速形成高密度的富铜析出相[50].如图3(a)所示,演化初期,Cu 和Mn 元素在相同的位置出现了成分起伏,磁化强烈影响最邻近原子的相互作用,特别是在Mn-Mn 和Cu-Cu 对的情况下,它们表现出不同的有序趋势.虽然Mn 原子在铁磁性(ferromagnetic,FM)状态下相互排斥,但Cu 原子之间却相互强烈吸引,且Mn 对Cu 原子也有强烈的吸引力,这是Cu 原子在原子团簇中的原因[11,51].Mn 和Cu 相互作用处的浓度略高于基体中浓度,并且此处的浓度不断增大,但不同的是,Cu 的浓度从最初的成分起伏一直聚集,核心Cu 的浓度远高于基体中Cu 的浓度,最终达到了99%,如图3(b)所示.

观察Mn 的成分曲线可以发现,Mn 元素先出现了成分起伏,核心处Mn 的浓度略高于基体其他区域,浓度达到最大值时,曲线顶点有凹陷趋势,说明在演化过程中,Mn 则从核心不断被“排挤”到核心周围形成环形富集区,如图3(c)所示.Cu 位于沉淀相的中心,而Mn 则偏析在沉淀相与基体之间的界面形成壳层结构,上述过程如图4(a)—(c)所示,最终形成以富Cu 相为核心,Mn 元素在外层形成环状的元素分布,如图4(d)所示,这种富Cu 沉淀相具有核-壳结构的现象也在文献[8,11,52−54]中被证实,这也与伪失稳分解特征相吻合,并且随着Cu 的富集长大,Mn 环尺寸随之变化,如图3(d)所示.

图3 温度为823 K 时IME 作用下Mn 与Cu 沉淀析出的成分曲线(原子含量) (a) 早期(t *=2500)时Cu 与Mn 的成分曲线;(b) 不同时间步数Cu 的成分曲线;(c) 不同时间步数Mn 的成分曲线;(d) Mn 环在不同时间步数的演化过程Fig.3.The composition curve of precipitation of Mn and Cu under the action of magnetic energy in 823 K (atomic percent):(a) The composition curve of Cu and Mn in early (t *=2500);(b) composition curve of Cu with different time steps;(c) composition curve with different time step size of Mn;(d) evolution process of Mn ring with different time steps.

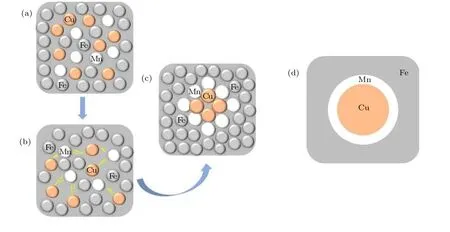
图4 Cu 原子和Mn 原子相互作用和局部元素分布示意图 (a)—(c) Cu,Mn 原子相互作用示意图;(d) Fe,Cu,Mn 局部元素分布示意图Fig.4.Schematic diagram of Cu atom and Mn atom interaction and local element distribution:(a)–(c) Schematic diagrams of Cu and Mn atom interaction;(d) schematic diagram of local element distribution of Fe,Cu and Mn.

4 讨论

4.1 影响IME 的因素

为什么图1(b)中α相与γ相的GFE 差值随温度升高而减小? IME 是如何作用于总GFE? 图5(a)是α相和γ相居里温度与Mn 含量的关系,根据(10)式和(11)式所得,α相的居里温度随Mn 含量升高而降低,且Mn含量为0.01 时的居里温度为1027 K,高于实验温度.图5(b)为α相和γ相的内磁能随温度以及Mn 含量的变化,可以发现α相的内磁能随温度升高而逐渐趋于0,且初始值随Mn含量升高而降低.根据图5(a)所示,Mn 含量降低了居里点,当温度接近并超过居里点时内磁能将逐渐减小且由铁磁性向顺磁性发生转变[55],故内磁能逐渐趋于0,对总自由能的贡献也随之减小.而γ相的居里温度变化趋势则与α相相反.在该实验温度条件下(Mn 含量0.01—0.03 区间,实验温度723—1123 K)远高于γ相的居里点,故γ的内磁能均近似于0,对总自由能的贡献可以忽略不计,这也解释了图1(b)中α相和γ相自由能在初始值的差值随温度不断增大而减小.结合图5(b)和图5(c)发现,随着Mn 含量升高,总自由能的最高值反而降低,说明在演化后期IME 对总GFE 的影响远低于纯组元GFE 的贡献.综上所述,IME 对成核阶段的影响作用最大,随着演化的进行,作用效果逐渐减小.

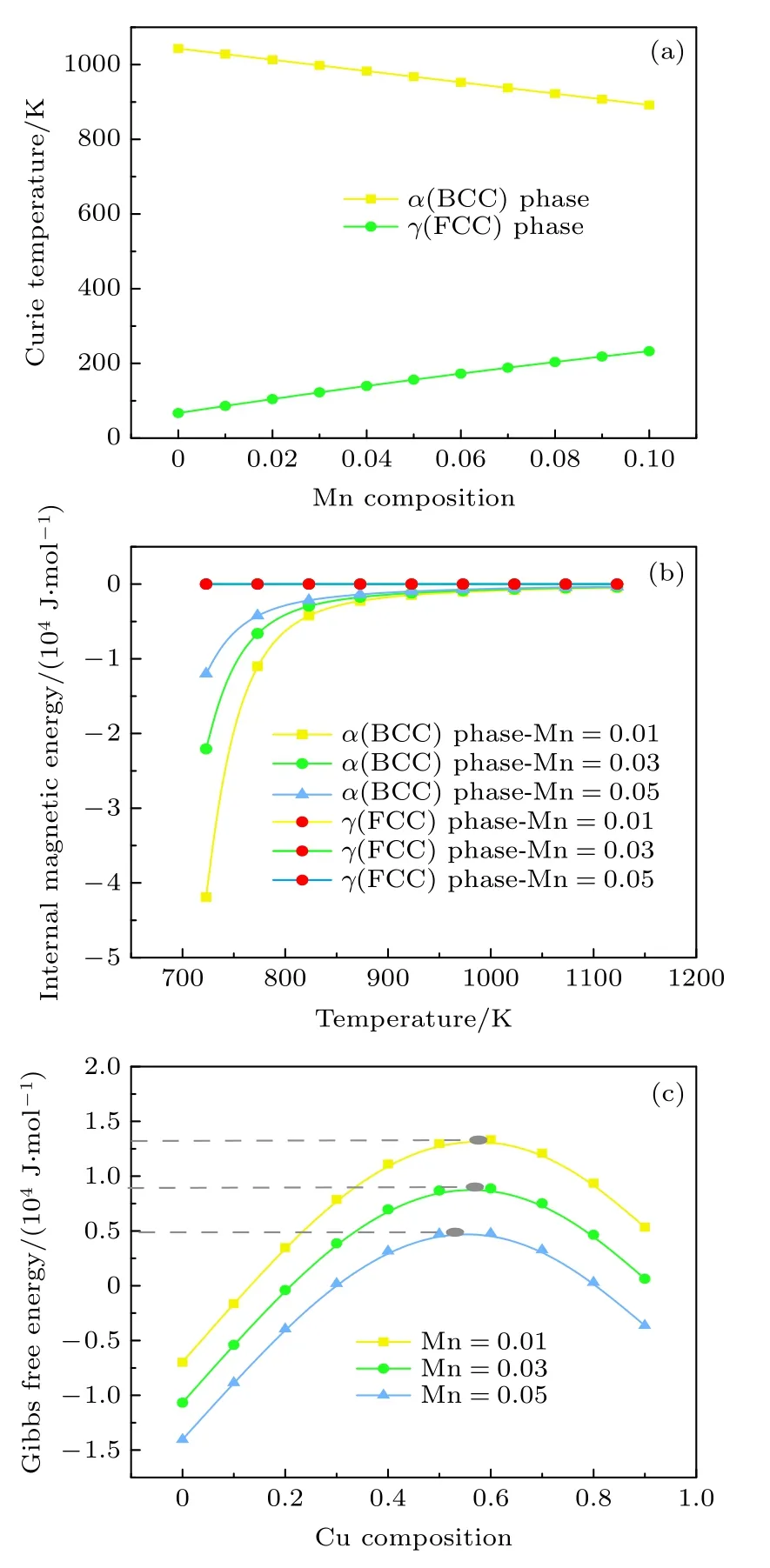
图5 温度为823 K (a) Mn 含量与居里温度的关系;(b) 温度与IME 的关系;(c) 不同Mn 含量下吉布斯自由能Fig.5.At 823 K (a) Relationship between Mn content and Curie temperature;(b) relationship between temperature and internal magnetic energy;(c) Gibbs free energy with different Mn content.

4.2 IME 影响沉淀相形貌的原因

研究表明,决定合金元素间相互作用特性的重要因素是基体的磁性状态[46,56].为了减少铁磁性元素含量对结果的影响,选取了非铁磁性元素Cu 含量为变量.如图6 所示,体积分数随Cu 含量的增大而增大,但值得注意的是,无论Cu 含量为多少,在IME 作用的影响下,总拥有更高的体积分数.并且在Cu 含量为0.15—0.35 范围内,有IME 作用下的体积分数均大于无IME 作用.因为磁性对Mn 的溶解过程都有重要的作用[46],Mn 在FM 状态下对Cu 原子也表现出明显的吸引力[11],如图3(a)所示,并且在演化过程中Cu 会在Cu-Mn 沉淀相的核心长大,而Mn 则偏析在沉淀相与基体之间,降低了沉淀相与基体相之间的界面能,减少了Cu 迁移的阻碍,进一步促进富Cu 相的析出[57].Mn 原子作为非常稳定的混合哑铃溶质[58],混合哑铃旋转不需要太多能量,因此Mn 溶质通过平移和旋转的机制进行迁移并进行团簇,而这些团簇又成为其他哑铃的缺陷[57],Mn 不断以这种机制在界面处富集,从而影响富Cu 沉淀相的演化过程.Mn在低含量时(<0.05)低温时IME 对总自由能的贡献最大,也就是说在演化早期的长大阶段,IME 对体系的贡献最大,影响了后期粗化阶段,故在IME作用下拥有更大的体积分数,也说明IME 对沉淀相的体积分数也有积极作用.故IME 对体系的体积分数的贡献也是不可忽视的.

图6 在有无IME 作用下体积分数随Cu 含量的变化Fig.6.Variation of volume fraction with Cu content with or without internal magnetic energy.

4.3 IME 对材料硬度的影响

文献[21]研究发现,与拉伸性能相比,硬度和磁性对RPV 钢的时效变化更为敏感,然而相结构的转变会给磁畴壁的移动带来额外的障碍[59],从而影响合金的IME,这种障碍也会随着沉淀相的增大而导致矫顽力达到最大值[60−62],富Cu 相会成为畴壁位移的障碍,并且在富Cu 相附近,磁矩会向磁晶各向异性的方向偏转,这种偏转畴壁的位移是富Cu 相导致矫顽力(coercivity)Hc增大的主要机制[63].根据上文,IME 会影响富Cu 相的析出,而由于富Cu 相的析出,基体中组成也发生了变化,从而导致Bs的变化,可见IME 通过影响富Cu 的析出而影响整个体系的磁性状态.其中,矫顽力Hc与平均颗粒尺寸D的关系为[64]

其中,C为材料有关的常数(居里常数),D为沉淀相颗粒的平均半径.值得注意的是,如图7(b)所示矫顽力与硬度近似线性的关系,可以估计材料硬度变化[21].相场模拟发现,在IME 作用下富Cu 相具有更大的平均颗粒半径,如图2 所示.根据(17)式,Hc与D的关系如图7(a)所示,相同实验条件下,考虑C为常数,D1Hc2,由此可得,具有较小平均颗粒半径的富Cu 沉淀相,拥有更大的矫顽力,又如图7(b)所示,硬度值随矫顽力而增大.因此IME 作用下Fe-Cu-Mn 合金的硬度值更小.

图7 矫顽力(Hc)与颗粒半径以及硬度的关系示意图(a) Hc 与平均颗粒半径的关系示意图;(b) Hc 与硬度关系示意图Fig.7.The relationship between coercivity (Hc) and particle radius and hardness:(a) Schematic diagram of relationship between Hc and average particle radius;(b) schematic diagram of relationship between Hc and hardness.

5 结论

IME 可降低相结构转变势垒,使得相结构转变所需要的能量较低,相较于无IME 作用下的Fe-Cu-Mn 合金更容易发生相结构转变.

Mn 含量与α相的居里温度呈反比,当Mn 含量从0.01 增至0.05 时,该合金α相居里温度从1027 K 降为967 K.在相同的居里温度下,IME 对总自由能的贡献随实验温度升高而减小.

在IME 作用下,富Cu 沉淀相拥有更大的平均颗粒半径以及平衡态时的体积分数和较小的矫顽力,根据矫顽力与硬度的线性关系,IME 作用下Fe-Cu-Mn 合金的硬度值更小

附录A

纯组元i吉布斯自由能和二元和三元的相互作用参数相关参数来源于文献[65,66].对于Fe-Cu-Mn三元合金体系而言,有3 个二元系Fe-Cu,Fe-Mn,Cu-Mn和1 个三元系Fe-Cu-Mn.因此二元和三元系的相互作用参数具体值为[37,65,66]: