双轮载下正交异性钢桥面板铺装层动力分析

郑一峰,李 想

(吉林大学建设工程学院,吉林 长春 130021)

一般的正交异性钢桥面板是指在桥面的面板下面采用纵横加劲肋加强的构造形式,其中采用U形纵向加劲肋的构造形式最为普遍。它由面板、U形纵向加劲肋以及横向加劲肋或横隔板组成。正交异性钢桥面板具有轻质高强、适用性强、施工效率高等优点,是现代钢桥结构重要的研究成果之一,也是目前中、大跨径钢桥尤其是大跨度钢桥采用最多的一种桥面板结构形式[1-4]。另一方面,在长期车辆作用下,易出现疲劳开裂、铺装层破坏等病害。从我国20世纪90年代修建此类桥梁的后期运营情况分析,其具有很大的理论价值和实际工程意义。此外汽车以较大的速度驶过桥梁时,汽车荷载将对桥梁结构产生较大的冲击力,动力效应显著[5-8]。随着汽车高速化、重型车占比等快速发展,这一问题势必将更加突出,而铺装层作为直接受力对象,其服役特性对整个体系而言显得尤为关键。

以某座大跨度钢桥为背景,借助大型通用有限元软件ANSYS自身强大的有限元建模、静动力分析能力,对正交异性钢桥面板铺装层的应力、变形进行数值模拟分析,并有针对性地进行基于双轮荷载简化模式下的单车移动荷载以及移动荷载列下铺装层的动力响应分析,由此分析得出一些有用结论和建议,以期为今后相关研究提供一定的理论参考。

1 计算模型及假设

为了保证正交异性钢桥面板和铺装层之间建立起合理的力学模型,作如下假设:

(1) 钢桥面板和铺装为均匀、连续和各向同性弹性材料[9-10];

(2) 认为铺装层与钢桥面板之间完全连续且无相对滑动;

(3) 计算模型均遵循小变形理论;

(4) 有限元模型横隔板底部采用完全约束,横向边缘保证无横向水平位移,纵向边缘保证无纵向水平位移,其中纵向为行车方向[11-12]。

对正交异性钢桥面板分析主要采用实体单元和板壳单元进行几何建模,继而进行有限元分析。对于正交异性钢桥面板和横隔板以及纵向加劲肋采用Shell63单元模拟;对于铺装层采用Solid45单元模拟;横隔板与加劲肋通过位置正交及弹性模量不同来实现正交异性。计算模型参考有关文献[13-14],沿桥面横向取7个U形加劲肋,沿桥纵向取3跨,包括4块横隔板。轮载区域网格划分尺寸精细化处理,其他区域采用相对粗略网格尺寸,模型共43 321个节点、38 563个单元,有限元模型如图1所示。模型尺寸及材料特性参考相关文献进行取值,具体参数取值见表1和表2。

图1 ANSYS局部有限元模型Fig.1 ANSYS local finite element model

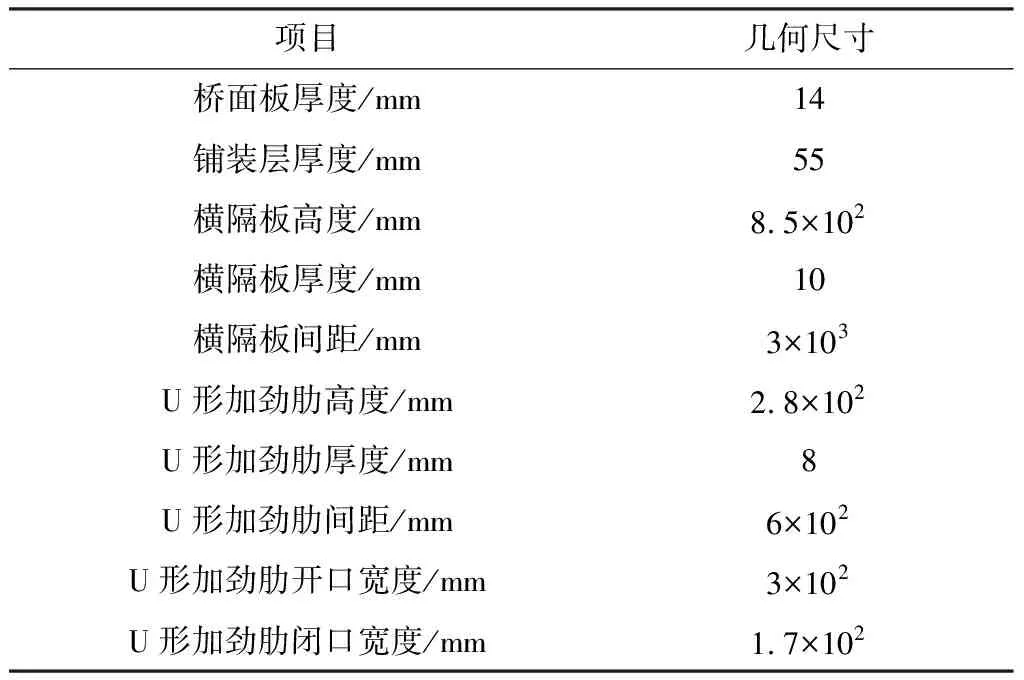
表1 模型各组成构件尺寸

表2 模型各组成构件材料参数

2 车辆荷载

2.1 车辆荷载的简化

参考《公路工程技术标准》相关条文,选取后轴重为140 kN的标准车,且单侧为双轮,单侧单轮胎压取0.75 MPa[15-16]。由于车轮实际作用面近似为矩形,将双轮荷载简化为2个矩形均布荷载,根据文献[17]矩形的横向尺寸取20 cm。依据轴重和胎压,计算出矩形纵向尺寸为23 cm,矩形间距取10 cm,双轮载简化情况如图2所示。

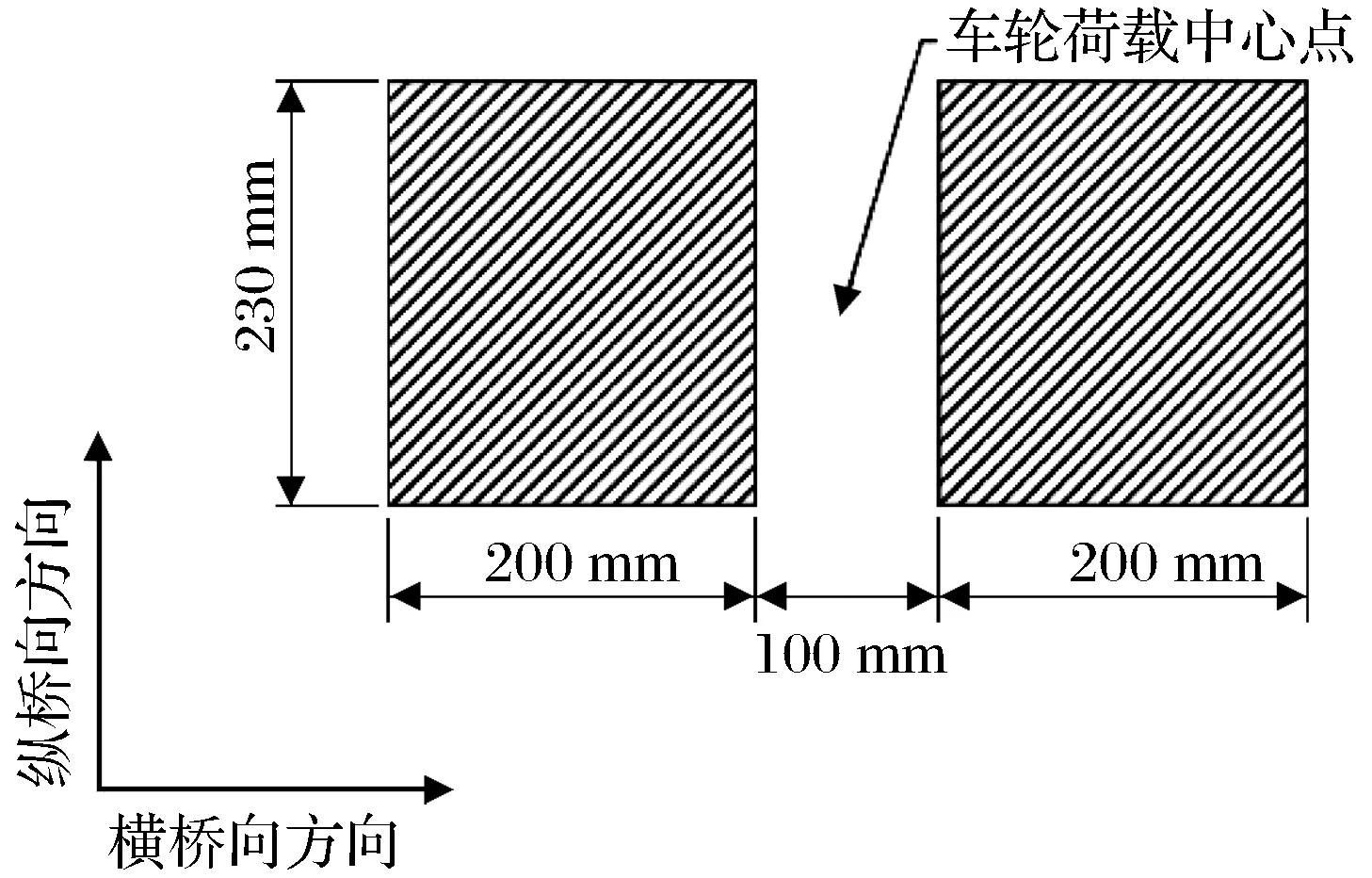
图2 简化的车轮荷载Fig.2 Simplified wheel loads

2.2 车辆荷载的加载方式

鉴于车辆行驶的实际情况,当车轮荷载距离某点较远时,该点的实际应力情况应趋于0,当车轮荷载刚好作用到该点时,其所受应力最大。综上可知,应采用三角形加载模式。其中纵桥向46 cm作为一个荷载步进行加载,依据已知的荷载步间距、车速可计算出双轮载中心移动至下一加载位置处所需要的时间t1。

3 静力分析

考虑到正交异性钢桥面板的结构特征,将轮压荷载在桥跨纵向作用在横肋中间,作为纵向最不利加载荷位[17]。由对称性考虑3种不同加载工况,作为横向特征荷位,利用ANSYS分别进行静力加载求解,以获取横桥向最不利荷位,横向加载荷位如图3所示,横桥向不同加载荷位下的ANSYS后处理分析结果汇总见表3～表5。

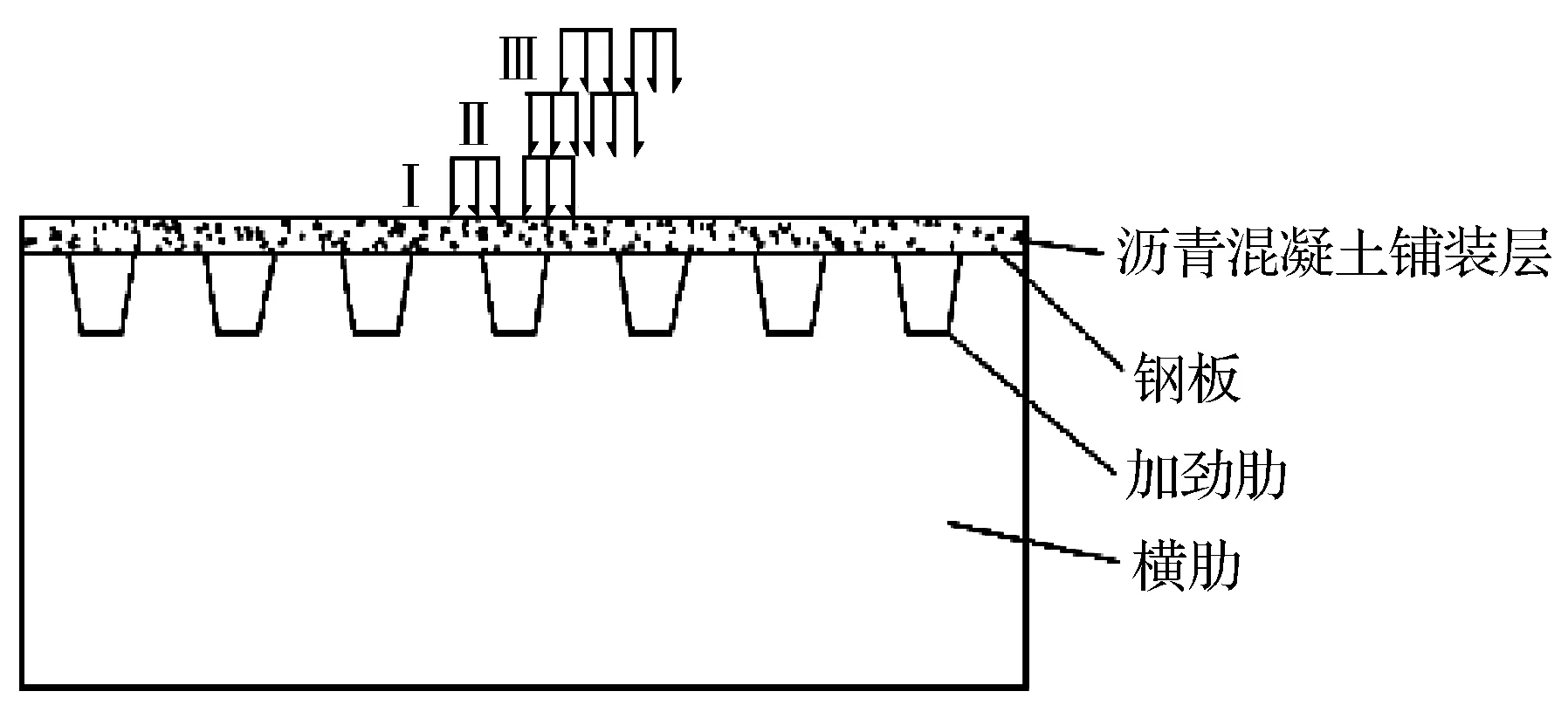
图3 横向加载荷位Fig.3 Lateral loading location

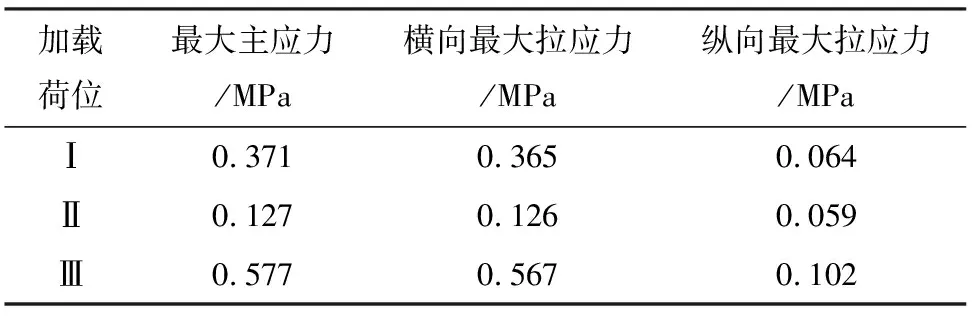
表3 横向不同荷位作用下铺装层最大拉应力及主应力

表4 横向不同荷位作用下铺装层最大竖向位移

表5 横向不同荷位作用下铺装层最大剪应力

从静力分析结果得出以下结论:

(1) 在车辆双轮轮压作用下,钢桥面板铺装层的受力呈现显著的局部特性,荷位Ⅰ、荷位Ⅲ竖向位移较大,荷位Ⅲ取得的最大值为1.230。

(2) 荷位Ⅰ处正交异性钢桥面板的最大主应力最大,横向最大拉应力、纵向最大拉应力次之。横桥向裂缝和纵桥向裂缝的控制应力的纵向拉应力、横向拉应力均在荷位Ⅲ处取得最大值。

(3) 在同一荷位作用下,铺装层与钢板的层间横向最大剪应力明显大于层间纵向最大剪应力,因此层间剪应力的控制方向是横桥方向,且在荷位Ⅲ处取得最大值。

(4) 当双轮荷载位于横向荷位Ⅲ时,正交异性钢桥面板受力最为不利,其主要原因是横向荷位Ⅰ～Ⅱ横跨2个加劲肋,载荷作用局部刚度得到较大加强,有利于应力的均匀分布和传递。

4 动力分析

把车辆轮压看成是移动荷载,鉴于当前对于单车移动荷载及相关参数的敏感性研究较多,考虑到一方面车流量日益增长,另一方面实际生活中是多车辆共同作用,单车作用的情况较少,故采用移动荷载列、双轮荷载进行模拟更符合实际情况。此外考虑共振以寻求最不利情况,这里采用等间距同类型标准车进行模拟。根据静力分析结果,动力分析选取荷位Ⅲ为最不利荷位,沿着最不利荷位进行纵向移动加载,进行单车移动荷载、移动荷载列下的动力分析(考虑重力影响)。已有研究及实测数据表明钢桥面铺装层的主要裂缝为横向拉应力控制的纵向裂缝,因而钢桥面铺装层拉应力控制应力为横向拉应力[18]。故选取铺装层竖向最大位移、横向最大拉应力、横向最大剪应力分别为分析参数Ⅰ～Ⅲ,且分析参数取得最值处分别设为计算点位Ⅰ～Ⅲ。

4.1 模态分析

结构采用瑞利阻尼输入,若已知前2阶模态阻尼比,则通过解一个二元一次方程组求解α和β,其公式为

2ζiωi=αi+βωi2。

(1)

模态分析表明计算模型的1阶自然频率为48.131 Hz,2阶自然频率为52.629 Hz。阻尼比ζ取0.05,利用式(1)计算得出瑞利阻尼比参数α=15.770,β=0.000 2 。

4.2 单车移动荷载

把双轮荷载看成是移动荷载,速度取72 km/h,沿着最不利荷位进行纵向移动。将模态分析得到的瑞利阻尼系数作为结构阻尼输入,利用ANSYS瞬态动力学分析功能进行单车移动荷载下的动力分析,计算各点位处的时程曲线,如图4～图6所示,各参数最大值结果分析见表6。

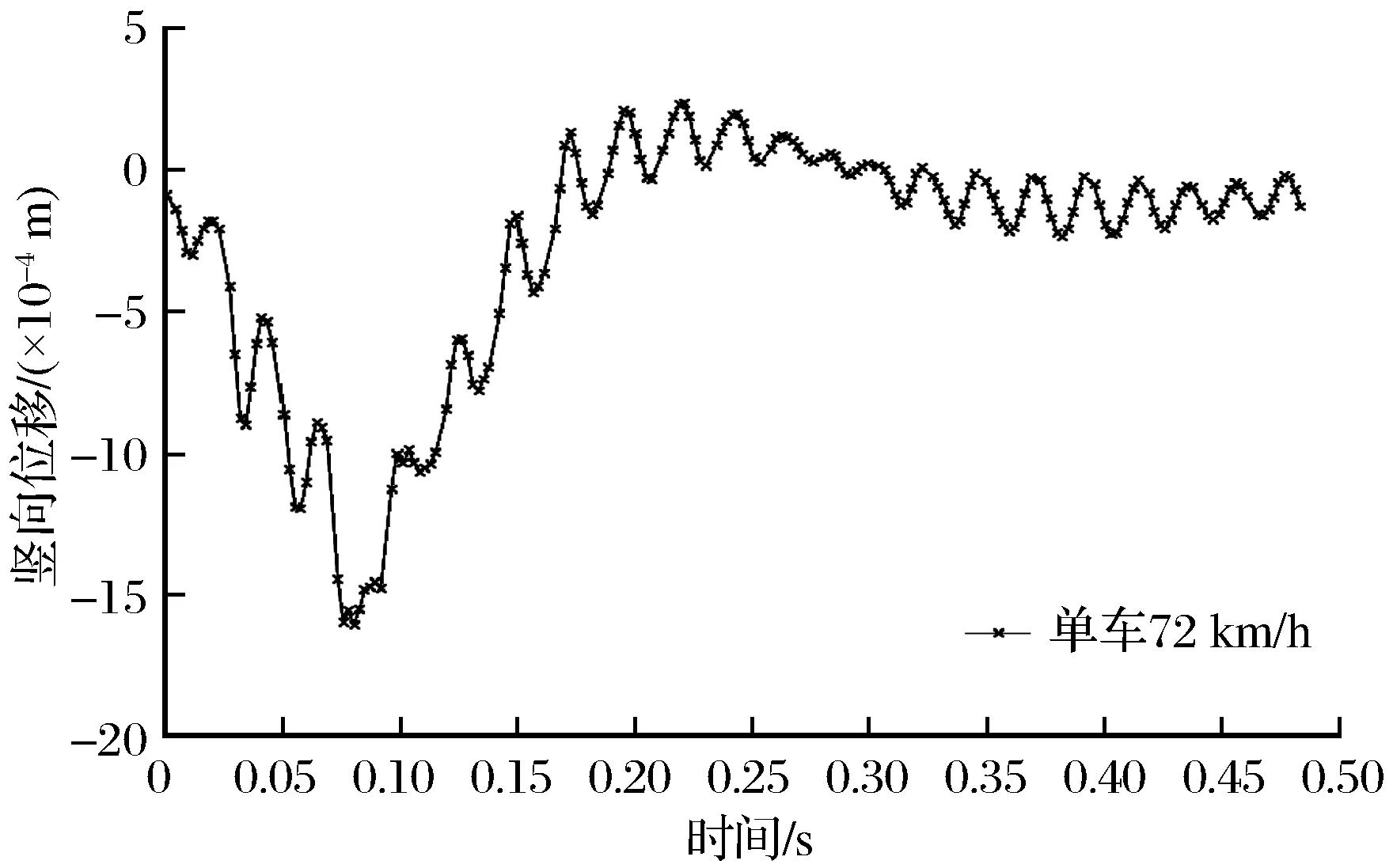
图4 计算点位Ⅰ处位移时程曲线Fig.4 The time history curve of displacement at point Ⅰ

从单车移动荷载分析结果得出以下结论:

(1) 在单车移动荷载作用下,铺装层表面的竖向位移随着车辆荷载的移动呈现出波动变化形式,竖向位移整体比静力荷载作用下的竖向位移大,最大增幅为30.57%,且局部效应明显,随着移动荷载离开,波动逐渐减小。

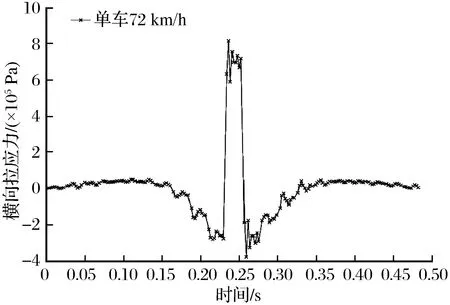
图5 计算点位Ⅱ处横向拉应力时程曲线Fig.5 The time history curve of lateral tensile stress at point Ⅱ

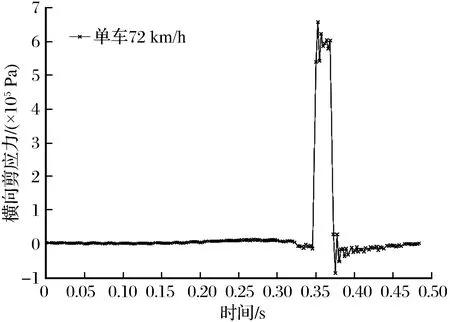
图6 计算点位Ⅲ处横向剪应力时程曲线Fig.6 The time history curve of lateral share stress at point Ⅲ

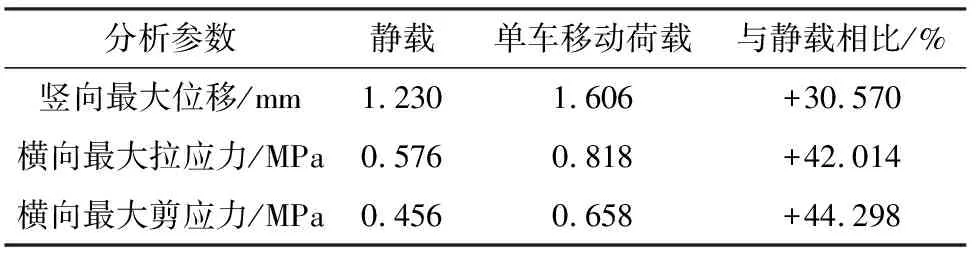
表6 最不利荷位下各分析参数最大值结果对比

(2) 横向拉应力具有类似阻尼振动,在荷载纵向移动的过程中,在接近最不利荷位的某个范围内,横向拉应力取得较大值,此范围内波动相对平缓,整体趋势呈先增后减,比静力荷载作用下的最大横向拉应力增加约42.01%;在即将到达不利荷位时,铺装层表面出现压应力,且压应力具有较强的局部效应。

(3) 横向剪应力在前段时间范围内整体波动平缓,随后急剧变化并取得较大值,较静力作用最大增幅为44.30%,在荷载离开计算点位后,变化趋于平缓,变化幅值很小,同样具有明显的局部效应。

4.3 移动荷载列

为了便于对比分析,分别取单车移动荷载72 km/h(基本速度)、移动荷载列72 km/h(基本速度)、移动荷载列86 km/h、移动荷载列100 km/h、移动荷载列115 km/h表示为工况1～工况5,相邻间距取一个荷载步的距离,研究车列、速度变化对于分析参数的影响规律。不同工况下各分析参数的时程曲线分别如图7～图9所示,各分析参数最大值对比见表7。

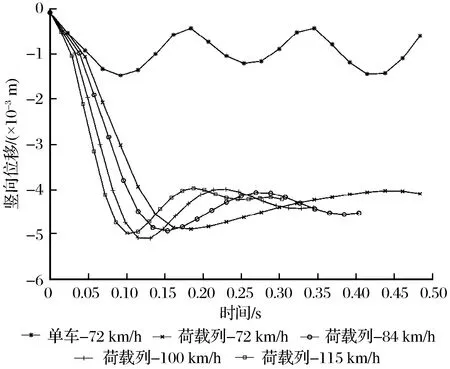
图7 不同工况下铺装层竖向位移时程曲线Fig.7 The time history curve of vertical displacement under different conditions

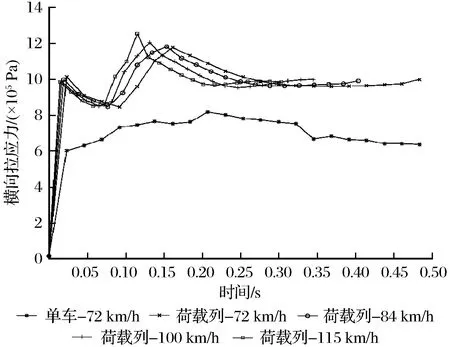
图8 不同工况下横向拉应力时程曲线Fig.8 The time history curve of lateral tensile stress under different conditions

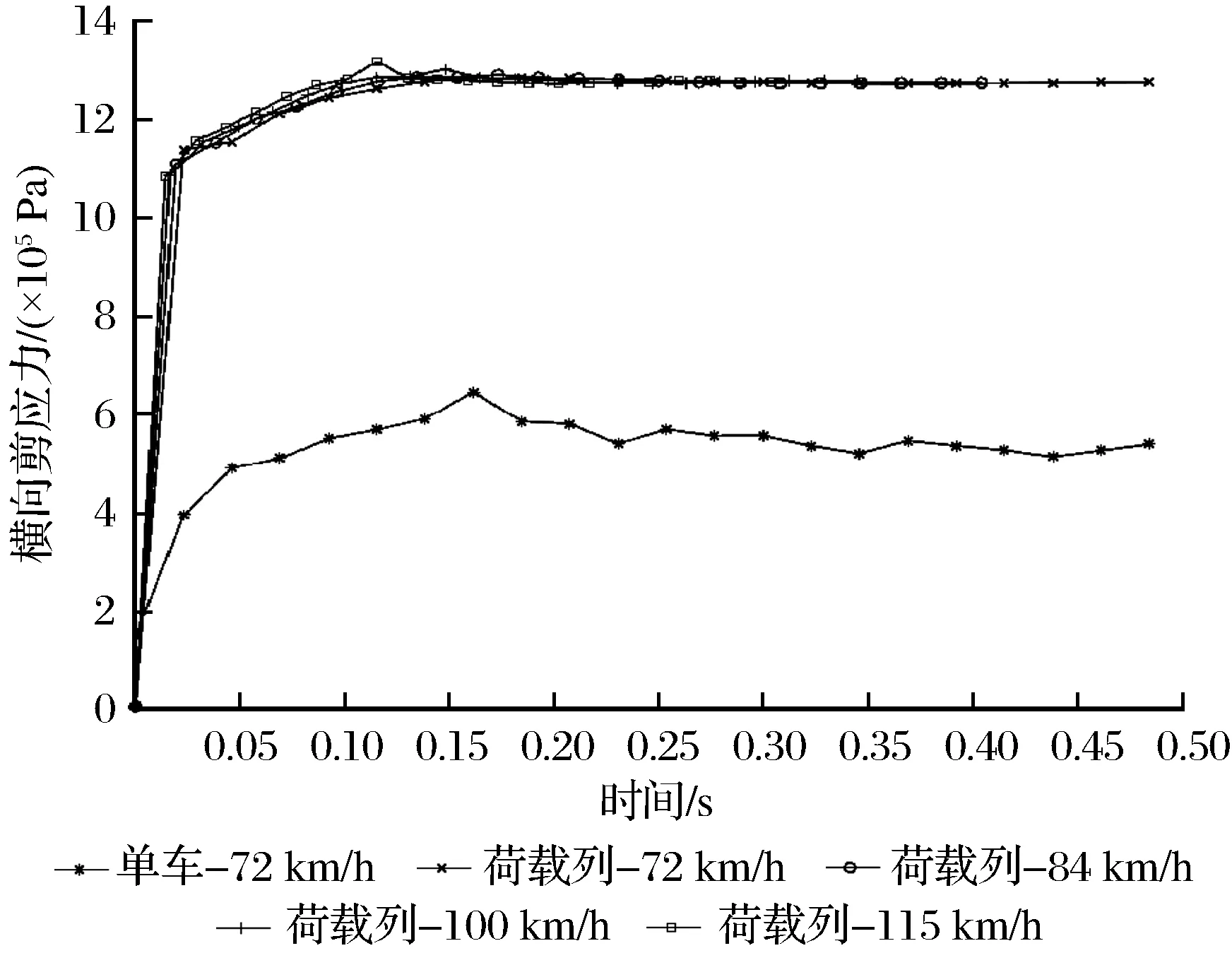
图9 不同工况下横向剪应力时程曲线Fig.9 The time history curve of lateral share stress under different conditions

表7 不同工况下分析参数最大值结果对比

从移动荷载列分析结果得出以下结论:

(1) 移动荷载列对最大竖向位移影响显著,速度相同时,较单车移动荷载,增幅可达206.25%,且整体变化趋势为先增大后减小并逐渐趋于稳定;不同速度下,随着速度提升,最大竖向位移先缓慢增加,后趋于稳定。

(2) 速度相同时,移动荷载列与单车移动荷载引起的横向最大拉应力相比,幅值提高了约43.89%,且整体变化趋势为先经历一个上升下降段后逐渐增大直至取得最大值,然后减小并趋于稳定;不同速度下,横向最大拉应力随着速度增大而变化微小。

(3) 横向最大应力对于移动荷载列较敏感,与同车速下的单车移动荷载作用结果相比,提高约95.29%。移动荷载列作用下的横向剪应力具有明显的非线性变化特点,先逐渐增大至最大值,然后开始减小,最终趋于稳定。不同速度下,随着速度的增大,最大横向剪应力有所增加,但增幅较小。

5 结论

通过对正交异性钢桥面板铺装层的静力及动力分析,得出以下几点结论:

(1) 当双轮轮压中心线位于纵向U肋边线时,正交性钢桥面板受力最为不利,这与以简化为单轮荷载时,钢桥面板最不利受力位置有很大不同。

(2) 移动荷载作用下,分析参数均较静力载荷有大幅提高,动力冲击效应显著,并且钢桥面板的受力呈现显著的局部特性。

(3) 横向最大拉应力、横向最大剪应力可作为铺装层控制应力。

(4) 相同速度下,移动荷载列作用下分析各参数最值较单车移动荷载作用下有大幅度提高;不同速度下,各分析参数随速度增大先缓慢增大,后趋于稳定,表现出非线性特点;分析参数中竖向位移及横向剪应力对移动荷载列表现较为敏感,横向拉应力次之。

(5) 应避免同类型车辆长时间保持等间距行驶,以打乱车流减少剪应力引起的铺装层剪切、滑移等病害;应适当控制车速以抑制各分析参数,减少铺装层病害的发生。

(6) 当考虑车桥共振时,应特别注意竖向位移以及横向剪应力的控制,以提高行车舒适性。