基于特征正则稀疏关联的无监督特征选择方法

白圣子，降爱莲

(太原理工大学 信息与计算机学院，山西 晋中 030600)

0 引 言

在原始高维数据集中，冗余特征的存在会影响学习算法的性能，降低学习算法的效率，甚至遭遇“维数灾难”。因此，需要通过特征选择，从原始数据中剔除无关、冗余等特征，选出具有代表性的特征构成最优特征子集，从而降低数据维度、简化学习模型、提高学习效率。由于数据规模较大以及获取数据标签十分耗时等原因，无监督特征选择在实际处理中更实用，研究其方法更具有挑战性[1]。

无监督特征选择方法根据评价准则主要分为过滤式方法、封装式方法和嵌入式方法[2]。过滤式方法独立于具体的学习算法，逐一对特征进行评分，如方差选择法[3]和拉普拉斯得分[4]选择法。封装式方法是根据后续使用的算法每次排除若干特征，直到特征数满足算法的要求，如递归消除特征法[5]。这两类方法评价标准单一，忽略特征之间的相关性，造成特征的冗余。嵌入式方法是将特征选择和训练模型的过程相结合，模型优化的同时直接计算出每个特征的权重，特征权重越大表明该特征越重要。如文献[6]将特征选择转化为矩阵分解问题，利用正则化矩阵分解方法选择出具有代表性的低维特征子集，但计算复杂度较高且正交约束条件很难应用到实际中。文献[7]提出特征级自表示选择方法，将特征选择问题转化为损失函数模型。该方法提出了数据集中的每个特征都可以被所有特征线性近似表示的性质，通过优化损失函数可以有效批量地评估每个特征的重要性。但在计算过程中，由于每个特征参与其自身的重构[8]，导致权重易向自身倾斜，无法合理地为每个特征分配权重。

针对上述问题，提出基于特征正则稀疏关联的无监督特征选择方法(feature regularized sparse association，FRSA)。该方法利用特征稀疏关联性质，能够合理分配特征权重，剔除冗余无关特征，降低数据维度，有效提升数据聚类准确率。

1 FRSA模型建立

1.1 最小二乘法线性回归

给定一个数据矩阵X∈Rn×m与响应矩阵Y=[y1,y2,…,yc]∈Rn×c，我们通常用如下公式来构建X与Y之间的线性关系

(1)

其中，W∈Rm×c是特征权重矩阵，l(Y-XW)是损失项，D(W)是对W施加的正则约束项，λ是一个正常数。式(1)的目标是得到一个合适的W，使得实际的响应矩阵Y与预测的XW之间的差值最小[9]。

1.2 特征稀疏关联

本文将数据矩阵X作为最小二乘回归模型中的响应矩阵Y来测量误差，学习特征权重矩阵W，揭示原始数据中特征之间的稀疏关联关系，即某一个特征可以被其它特征(不包含自身)稀疏近似表示。具体地说，给定m个特征，我们所运用的特征稀疏关联是学习每个特征与其它所有特征之间的线性近似关系。当i=j时，令wji=0，第i个特征不参与自身重构表示

f1≈f10+f1w21+…fiwi1+…+fmwm1

f2≈f1w12+f20+…fiwi2+…+fmwm2

⋮

fm≈f1w1m+f1w2m+…fiwim+…+fm0

(2)

因此，数据矩阵X中的每一个特征fi可形式近似表示为

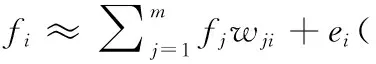
(3)

其中，ei是误差项，wji是表示系数，fi是数据矩阵X的一个特征。对于所有的特征，式(3)可以写成

X=XW+E

(4)

其中，W∈Rm×m与E∈Rn×m分别是特征权重矩阵和残余误差项。W有效地表示了不同特征之间的关联关系，并且使得残余误差项E(E=X-XW)尽可能得小。

1.3 目标函数

本文利用Forbenius范数来度量误差大小，期望得到一个合适的W，使得重构后的矩阵XW能够很好地近似表示原始数据矩阵X。如果X是一个单位矩阵使得误差项E≡0，则W为平凡解。因此，必须添加正则化项D(W)对特征权重矩阵的解空间进行约束，防止过拟合，降低模型复杂度，得到稳定可行的最优解[10]，进而得到了如下最小化问题

(5)

(6)

2 优化算法

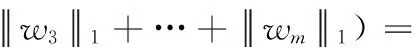
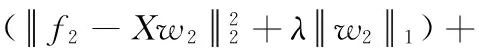
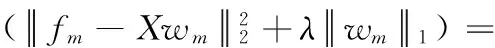
因此，原目标函数展开得到如下m个子问题

(7)

根据特征稀疏关联关系，第j个特征不参与自身的线性近似表示，因此wj的第j个元素为0。在实际计算过程中，需要删除数据矩阵X的第j列与wj的第j个元素

(8)

ϖj∈R(m-1)×1是wj删除第j个元素0后得到的特征向量，Xj-∈Rn×(m-1)是数据矩阵X删除第j列得到的数据矩阵，这样保证了第j个特征不参与自身的线性近似表示。针对式(8)的正则化回归问题，将利用一种收缩阈值迭代算法求其最优解。

首先考虑式(8)无正则化约束下的连续可微函数最小化问题

(9)

s.t.∀ϖ,y∈Rn

(10)

(11)

对于g(ϖ)最小的常数K称为李普希茨常数L。同时，在ϖk附近可将g(ϖ)通过二阶泰勒式展开

(12)

式(11)得出李普希茨常数L形式与二阶导数形式相似。基于此，在ϖk附近可以把函数值近似为

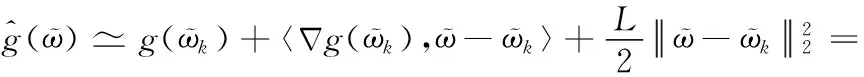
其中，后两项是与ϖ无关的常量。显然，式(12)的最小值在如下ϖk+1获得

(13)

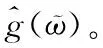
(14)

即在每一步对g(ϖ)进行梯度下降迭代的同时考虑1-范数最小化。

(15)

其中，不存在ϖiϖj(i≠j)这样的项，即ϖ的各分量互不影响且1-范数是可拆分函数，可得最优闭式解[15]。

对于式(15)中的每一个分量，都可以通过偏导求其最小值

(16)

(17)

其中，sign(x)为符号函数，如果x大于0，则为1；如果x小于0，则为-1；如果x等于0，则为0。考虑到式(15)两边都有ϖi，利用收缩阈值迭代[16]进行求解

(18)

综上所述，得出式(8)的优化迭代公式

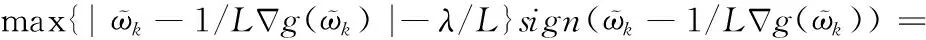
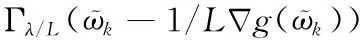
计算g(ϖ)在ϖk处的偏导，最终得到收缩阈值迭代式

ϖk+1=Γλ/L(ϖk-2/L(Xj-)T(Xj-ϖk-fj))

(19)

文献[16]已验证，若X为数据矩阵，当李普希茨常数L=2βmax(XTX)(βmax(·)表示矩阵的最大特征值)，式(19)得以快速求解。该式每次使用前一步迭代求得的近似函数最小值点ϖk作为下一步迭代的起始点，收敛速度为O(1/k)。为了加快其收敛速度，将引入梯度加速策略Nestrerow加速技术[17]

(20)

(21)

其中，Nestrerow加速使用前两步迭代过程的结果xk-1，xk，对其进行线性组合生成下一步迭代的近似函数起始点yk+1。经验证[17]，该加速技术适用于式(19)的收缩阈值迭代算法，以极少的额外计算量提高了算法的收敛速度。因此，引入Nestrerow加速后，式(19)为如下迭代形式

(22)

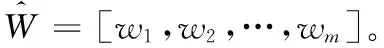
算法1：

输入：数据矩阵X∈Rn×m，特征选择个数d，正则项参数λ；

输出：特征子集D∈Rn×d；

(1)数据矩阵X→{f1,f2,…,fm}；

(2)将式(6)划分为m个子问题：

(3)计算L=2βmax((Xj-)TXj-)，初始化y1=ϖ0，t1=1；

(4)重复(k≥1)：

ϖk=Γλ/L(yk-2/L(Xj-)T(Xj-yk-fj))

(5)直到收敛；

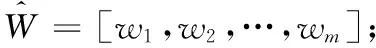
在引入Nestrerov加速后，收敛速度从O(1/k)提高到O(1/k2)。式(17)求偏导时(Xj-)TXj-的计算复杂度为O(nm2)，所以每个子问题的计算复杂度为O(nm3/k2)。因为FRSA模型的最优解是由m个子问题的最优解整合得到，所以该算法的整体计算复杂度为O(nm3/k2)。

3 实验分析

3.1 实验数据

为验证本文方法的性能，在机器学习数据库中选取了6个标准数据集进行对比测试，各数据集的详细参数见表1。

表1 实验数据集参数汇总

3.2 实验对比方法

为了验证本文提出的FRSA方法的有效性，实验中将其与以下4种常用的无监督特征选择方法进行比较：

(1)拉普拉斯得分特征选择方法[18](Laplacian score feature selection，LS)；

(2)无监督判别特征选择方法[19](unsupervised discriminative feature selection，UDFS)；

(3)矩阵分解特征选择方法[20](matrix factorization feature selection，MFFS)；

(4)自表示特征选择方法[7](self-representation feature selection，SR-FS)。

3.3 实验设置

在本实验中，采取3种被普遍应用的评价指标，即聚类准确率(accuracy，ACC)、归一化互信息(normalize mutual information，NMI)和冗余率(redundancy rate，RED)来评价不同无监督特征选择方法的性能。对于一个输入样本xi，qi和pi表示它的聚类结果和真实标签，那么ACC的定义如下

(23)

其中，函数δ(x,y)用于判断x与y是否相等，若相等则函数值为1，否则函数值为0。map(qi)是一个最佳映射函数，它的功能是通过Kuhn-Munkre算法把实验得到的聚类标签与样本的真实标签进行匹配[21]。ACC的值越大说明聚类性能越好，表明获得的聚类标签更加接近样本真实的标签。

归一化互信息是评价聚类结果好坏的常用指标之一，给定任意两个变量P和Q，NMI可以被定义为

(24)

其中，H(P)和H(Q)分别表示P和Q的熵，I(P,Q)是P和Q两者之间的互信息。P是聚类结果，Q是实际标签。类似于ACC，NMI的值越大意味着聚类性能越好。

冗余率[22]是用来度量数据的特征之间是否具有较强的相关性。假设fs是所选择的特征集，冗余率计算公式如下

(25)

其中，ρij是特征fi与特征fj之间的相关系数。RED(fs)的值越大意味着选择后的许多特征仍然是显著相关，冗余程度高。因此计算所得的冗余率越小越好。

在实验中将对每个无监督特征选择方法的参数进行设置。对于所有方法，每个数据集选择特征的个数范围设置为 {20，30，40，50，60，70，80，90，100}。对于LS、UDFS算法，将它们的近邻参数k设置为5。对于有正则项参数的算法，采用交替网格搜索的方式确定它们的值，其网格搜索范围设置为 {0.001，0.01，0.1，1，10，100，1000}[6]，并记录其中最优参数所对应的最好结果。然后将9个不同维数的特征子集的聚类准确率、归一化互信息以及冗余率分别取平均值，作为评价各方法性能的指标。

当利用K-means算法对每种方法选择的低维特征进行聚类时，考虑到K-means聚类的性能会受到初始质心选取的影响，为提升结果准确度，将重复执行150次不同的随机初始化实验，然后记录平均结果。

3.4 实验结果与分析

利用合成数据集IRIS-20测试本文提出的FRSA方法是否能找到具有代表性的特征。该数据集包含150个样本和20个特征，后16个特征是由前4个特征线性组合得到(组合系数随机生成并且和为1)，并加入了一定的高斯白噪声。

图1 特征权重直方图

从表2和图2(e)的实验结果可知，FRSA方法在Lung_discrete、Pronstate_GE、lymphoma、ORL和Urban这5个在数据集中所选择的特征子集获得最高的聚类准确率(ACC)，在数据集COIL20上的聚类准确率仅次于MFFS方法。从表3和图2(c)的实验结果可知，FRSA方法在Lung_discrete、Pronstate_GE、ORL、COIL20和Urban这5个在数据集中所选择的特征子集获得最高的归一化互信息(NMI)，在数据集lymphoma上的归一化互信息仅次于SR-FS方法。聚类准确率和归一化互信息都是评价聚类结果好坏的常用指标，因此得出结论，FRSA方法选择出的特征更具有代表性，可以有效地提高聚类准确率。从表4和图2(c)、图2(d)的实验结果可知，FRSA方法在Lung_discrete、Prostate_GE、COIL20和Urban数据集上选出的特征子集的冗余率(RED)最低，在数据集lymphoma上的冗余率仅次于SR-FS方法，在数据集ORL上的冗余率仅次于MFFS方法。冗余率越低，冗余程度越低。表明FRSA方法选出的特征之间冗余程度较低，特征子集冗余率较低，更具有代表性。

表2 不同特征选择算法的聚类准确率ACC/%

表3 不同特征选择算法的归一化互信息NMI/%

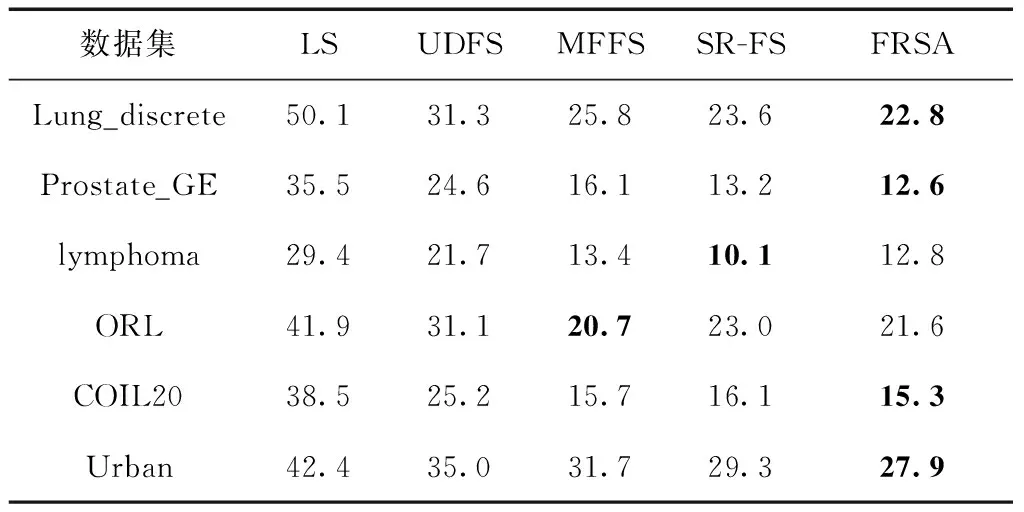
表4 不同特征选择算法的冗余率RED/%

图2 5种无监督特征选择方法在6种不同数据集上的ACC、NMI、RED对比

通过以上分析可以得出，由于LS方法是对特征逐一进行评分选择，并且没有考虑特征之间的相关性，因此在其3个评价指标上明显弱于其它方法。UDFS、MFFS、SR-FS方法都是基于正则化选择，并且都是对特征进行批量选择，因此在特征选择时，批量选择的效果优于单个选择。但是，UDFS方法更多地是考虑样本之间的相似，容易忽略特征之间潜在的相关系。MFSS方法是从子空间学习角度进行特征选择，也没有考虑特征之间的相关性。而SR-FS方法虽然利用特征级自表示性质选择特征，考虑特征之间的相关性，但不足之处是特征参与自身重构时容易使特征权重向自身倾斜，导致权重分配不合理。因此，本文在特征级自表示的损失函数模型框架下，利用特征互表示的性质[8]，学习每个特征之间的关联关系，提出了基于特征正则稀疏关联的无监督特征选择方法(FRSA)。该方法不仅利用稀疏正则化约束对特征进行批量选择，而且考虑到每个特征与其它特征(不包括自身)的关联性。实验结果表明,该方法所选出的特征子集具有较好的聚类效果和较低的冗余度，性能优于其它4种常用的无监督特征选择方法。在计算复杂度方面，UDFS方法、MFSS方法和SR-FS方法采用矩阵直接迭代逼近最优解，计算时间与空间复杂度较高[23]。而分治-收缩阈值迭代算法将矩阵整体优化问题拆分为多个性质相同的向量优化问题，然后再进行迭代求解，占用内存较小且计算效率高。因此，FRSA方法有较低的计算复杂度。

4 结束语

在本文中，利用无标签数据特征之间潜在的关联性，提出了一种基于特征正则稀疏关联的无监督特征选择方法(FRSA)。利用L1-稀疏规则算子在特征选择时对权重矩阵施加正则化约束，最小化其非零行数，加强了特征权重矩阵的行稀疏性，提升了所选特征子集的鲁棒性。通过稀疏关联性质克服了特征权重易向自身倾斜的不足，合理地为每个特征分陪权重。实验结果表明，FRSA方法可以有效地评估每个特征的重要性，选择出重要特征，剔除冗余特征，降低原始高维数据的冗余率，提高聚类准确率，并且具有较低的计算负责度。在实际应用中，获取的数据不够完善不具有多样性[24]，后续工作可以进一步扩展方法适用于不完整数据。另外，正则化约束项[25]对权重矩阵的作用直接影响到FRSA方法的性能，如何构建更有效的正则化约束项也是下一步研究重点。