基于SURF的改进FLANN匹配算法

张志敏，李 彬+，田联房，丁焕文

(1.华南理工大学 自动化科学与工程学院，广东 广州 510641；2.华南理工大学 医学院，广东 广州 510006)

0 引 言

计算机辅助骨科手术系统有卓越的表现，受到各国骨科医生的高度重视[1]，同时诸多研究结果表明在计算机辅助骨科手术中应用增强现实技术[2](augmented reality，AR)具有非常高的临床应用价值。AR技术的实现依赖于视频图像，需要对其中的目标进行检测匹配跟踪。但由于视频图像中复杂目标、光线及视角变化等因素影响，使得视频图像的目标检测匹配成为了一个颇具挑战的问题。研究人员为解决这一难题提出了许多不同的视频图像匹配方法，其中基于SURF[3,4]特征点匹配方法最适合于视频图像匹配。近些年，很多学者对SURF特征点做了大量的研究，提出了不同的改进方法。Shene等[5]改进了SURF特征点的提取步骤；Oszust等[6]对SURF特征点的描述符算子进行了改进；Feng等[7]提出了改进的匹配方法。但这些改进的算法仅适用于简单的图像特征点匹配或者视频的个别帧图像匹配，无法直接应用到视频连续的帧图像中。

基于上述背景，本文针对视频图像匹配提出了一种基于SURF特征点的改进FLANN[8,9]匹配算法。首先改进了SURF特征点的描述符算子，然后以FLANN算法为基础，结合随机抽样一致性(random sample consensus,RANSAC)算法，剔除大量误匹配、无用的特征点，从而大幅提高匹配速度。经实验验证，本方法的稳定性及快速性较好，能够在计算机辅助骨科手术系统中实现AR的过程，有效辅助医生对骨科手术患者中病灶区域的定位。

1 基于SURF特征点的改进FLANN视频图像匹配算法概述

本文提出的基于SURF特征点的改进FLANN图像匹配算法。算法的流程如图1所示。

图1 基于SURF特征点的FLANN视频图像匹配算法流程

2 基于改进的SURF特征点提取

SURF是SIFT的加速版，具有旋转尺度不变特征，其不但能测出图像中的关键点，稳定描述关键点的局部信息，而且理论上是SIFT算子速度的3倍。

2.1 基于Hessian矩阵行列式的特征点提取

提取SURF特征点的过程，首先是用图像的Hessian矩阵行列式构成SURF尺度空间，用非极大值抑制提取特征点。特征点受Hessian行列式阈值的影响，阈值越大得到的特征点的鲁棒性越好，实际中需要适当的调整阈值。

2.2 改进的SURF特征点描述符

在复杂的视频图像匹配中，由于匹配对图像特征点描述的局部信息依赖性较高，单个特征点不足以描述该特征点的局部区域信息。针对此问题，在不改变SURF特征点原有的旋转尺度不变性的前提下，本文提出了改进的特征点描述符，在特征向量中加入了特征点4-领域内的特征点描述符信息。

在构成的SURF尺度空间中提取到的特征点，用f0表示该特征点原有的描述符。在图像中该特征点的4个方向距离10 s(s为特征点所在的尺度)的特征点分别用f1、f2、f3、f4表示。为了使该特征点能够更准确地描述局部信息，构建特征点4-领域的描述符f1、f2、f3、f4都使用f0的主方向，以确保特征点的旋转不变性。然后由该特征点及其它4个特征点描述符构建新的描述符，作为特征点的特征向量，表示为v={f0,f1,f2,f3,f4}。新构成的特征点不仅保留SURF特征点原有的旋转尺度不变性，还加大对局部信息的描述，对复杂的目标有更大的区分度。

3 基于SURF特征点的改进FLANN匹配算法

SURF特征点的匹配主要是通过Lowe等提出的FLANN算法来匹配，该算法是通过判断两特征点的欧氏距离来确定匹配度。然而FLANN算法的匹配速度并不满足视频图像匹配的需求。因此本文提出了一种改进的FLANN搜索算法，在原来的基础上结合RANSAC算法，剔除无匹配、误匹配的特征点，进一步提升匹配速度。

FLANN匹配算法需要两两计算求出最佳匹配点对，其中误匹配、不相关的特征点也参与到计算，而RANSAC算法则需要对特征点进行多次迭代，求出概率最大的模型，均不符合视频图像匹配快速性的要求。因此本文提出了一种改进的FLANN算法，其结合了RANSAC算法的思想来剔除大部分不相关的特征点以达到快速匹配的效果。在现实场景中图像常被检测出大量无用的SURF特征点，在提取SURF特征点之前先对原视频图像序列进行下采样，以减少一部分不必要的特征点。其次在计算两点的欧氏距离之前先利用他们的迹做初步筛选，特征点迹的符号相同即表示两特征点具有相同方向上的对比度变化。改进算法的流程如图2所示。

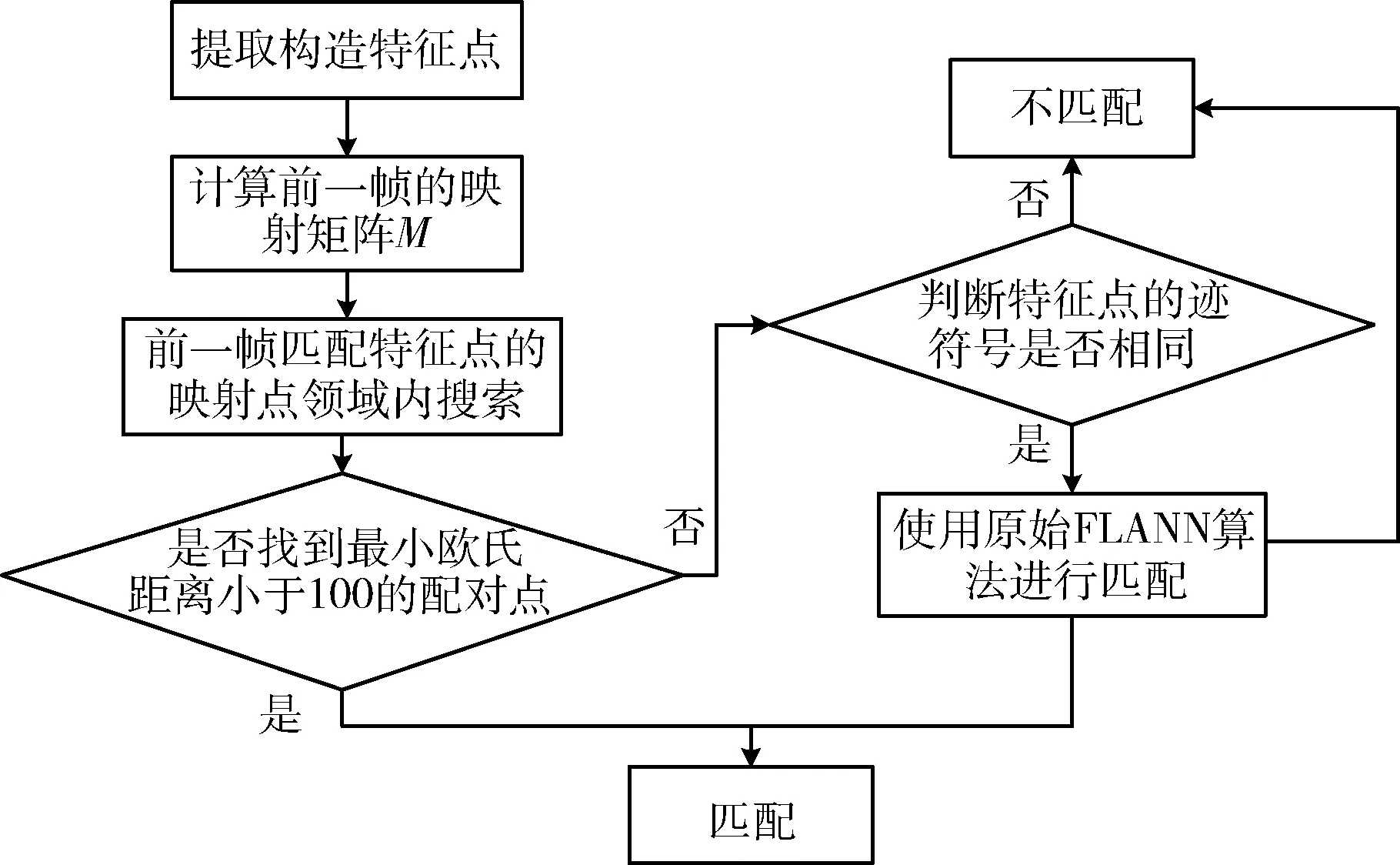
图2 改进的FLANN算法流程

改进的FLANN匹配算法步骤如下：

(1)在原来的FLANN算法中，利用RANSAC[10]算法增加特征点的匹配先验信息，以减少大量的配对计算。首先根据前一帧图像求得的匹配点对，利用RANSAC算法求出配对点之间的映射关系；

原来的RANSAC算法是通过迭代循环找出一个数据集的模型。RANSAC每次迭代都随机选取4组特征点计算出它们的映射关系，统计符合该映射的特征点。迭代一定次数后选出符合特征点数量最多的模型作为最终模型。

将RANSAC算法加入到FLANN算法中。由于前一帧已经求得最佳的配对点，故不需要迭代，只需从前一帧中配对好的特征点选出4组即可求出映射矩阵H。其中的映射关系如式(1)所示

(1)

其中，(x′,y′)是特征点(x,y)的映射点坐标，H是映射矩阵。映射矩阵H的求解可将式(1)展开，得到式(2)

(2)

将式(2)整理可得式(3)

(3)

由于变换矩阵H可进行任意尺度缩放，故令h33=1。每组匹配的特征点可以得到两个方程组，因此通过4组特征点可得4组方程(3)，即可算出矩阵H的8个参数，得到矩阵H。求得映射矩阵进入步骤(3)。

若当前帧是视频的第一帧或者上一帧没找到配对点则跳过这步进入步骤(3)，直接用原来的FLANN算法求配对点。

(2)在FLANN算法中，根据RANSAC算法增加了配对点的预测区域，在局部区域搜索配对点。通过计算特征点p0(x0,y0)的预测配对点，以该预测点的30领域作为配对点的预测区域。首先通过式(1)计算出p0的映射点坐标，然后优先在映射点的30领域内搜索配对点，找到与p0点领域内有最小欧氏距离的配对点。

假设两个m维特征向量分别为p(xp1,xp2,…,xpm)、q(xq1,xq2,…,xqm)，则他们的欧氏距离Dpq如式(4)所示

(4)

在p0的映射点领域内有很大概率可以找到最小欧氏距离小于100的最佳配对点，因为通常前后一帧图像移动范围会比较小。否则进入步骤(3)和步骤(4)继续调用原来的FLANN算法搜索剩余的特征点。

(3)在进行FLANN算法匹配之前，先对特征点的迹符号归类，以进一步筛选配对点，减少配对计算量。判断两个特征点的迹符号是否相同，若符号相同再进行下一步，否则跳过欧氏距离计算直接判为不同点，如式(5)所示

(5)

(4)FLANN算法的核心是计算两特征点的欧氏距离。通过判断距离某SURF特征点最小欧氏距离和次小欧氏距离的比值是否低于某阈值，来筛选该特征点是否存在唯一的匹配点。可通过式(6)进一步筛选特征点匹配对

(6)

式中：Dpq为距离特征点p的最小欧氏距离，Dpk为距离特征点p的次小欧氏距离。T为比率阈值，本文经过多次实验得出T=0.6最为合适。

使用改进的FLANN算法进行特征点匹配时，只要视频画面不是高速移动，该算法都可以找到特征点对应的配对点。高速移动也会出现视频丢帧或帧模糊的情况，这种情况也无法找到相应的配对点。

4 三维模型的构建与位姿估计误差

4.1 三维模型的构建与初始化

本文用于匹配的三维模型是实际患者的三维骨骼模型，是由医学图像DICOM序列经过一系列的解析、处理后，通过Marching Cubes[11]面绘制算法构成的，它可以反应出患者的真实信息，为辅助医师诊断提供更多的信息。

得到的三维模型结果由于其原点坐标不在其中心位置，旋转、平移等操作不绕其中心位置变化，人机交互性很差，因此在匹配初始化时，首先加载三维模型，并对其坐标初始化，使原点在其中心位置。初始化主要是将三维模型的每个三角形面片中心Ci与对应的三角形面片的面积Si的乘积累加求和，再除以总的三角形面积的加和S便得到模型的中心C。如式(7)所示

(7)

然后将每个三角形面片的顶点坐标减去中心位置C，得到三维模型新的坐标，即可在不改变三维模型的形状、相对位置的情况下将其坐标同一化。本文提出的算法是通过手动选取初始特征点，因此在初始化时，首先要确定三维模型世界坐标空间中的4个坐标点，然后在二维图像中选取对应的点才能做进一步的目标跟踪。

4.2 三维模型的位姿估计误差

在二维图像与三维模型上选取了4组匹配的特征点后，经过PNP问题[12-14]的求解，可以得到三维模型世界空间坐标系的旋转矩阵R和平移矩阵t，即可在实时渲染三维模型时对目标进行相应的旋转和平移，最终在二维屏幕上表现出相应的姿态。

三维模型的位姿估计会出现误差，主要是来源于三维模型的初始化位置、二维图像特征点的匹配跟踪的误差以及三维模型位姿求解误差。三维模型的位姿估计结果是求得旋转矩阵R和平移矩阵t，其旋转误差计算需要将旋转矩阵R转换为对应的旋转角度(θx,θy,θz)，如式(8)所示

(8)

式中：rij是旋转矩阵的第i行第j列的元素。然后按式(9)计算旋转误差ER和式(10)计算平移误差Et

(9)

(10)

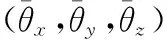
5 结果讨论

本文通过实验验证提出算法的稳定性和快速性。为了模拟手术场景，实验所采用的三维模型是由军区总医院提供的脊柱CT经三维重建得到的模型，并将对应的三维模型3D打印出来，用于替代手术中的患者。实验中使用的摄像机是钰创免驱摄像头驱动2012版：分辨率是640*480，最大帧率：50 Hz，视频编码格式：YUY2/MJPG。实验的硬件环境为：CPU Intel(R)Core(TM)i5-3230M，主频2.60 Ghz；内存8.00 GB。软件环境为：Microsoft Visual Studio 2013、Qt5.60。

5.1 实验结果

为了验证结果，实验一共使用10组不同的人体脊柱三维模型来验证本文提出的算法。

5.1.1 实验数据

所使用的CT图像序列是由广州军区总医院提供的脊椎CT图像序列，如表1所示，每个序列切片数量约为200～500张。部分CT切片效果如图3所示。

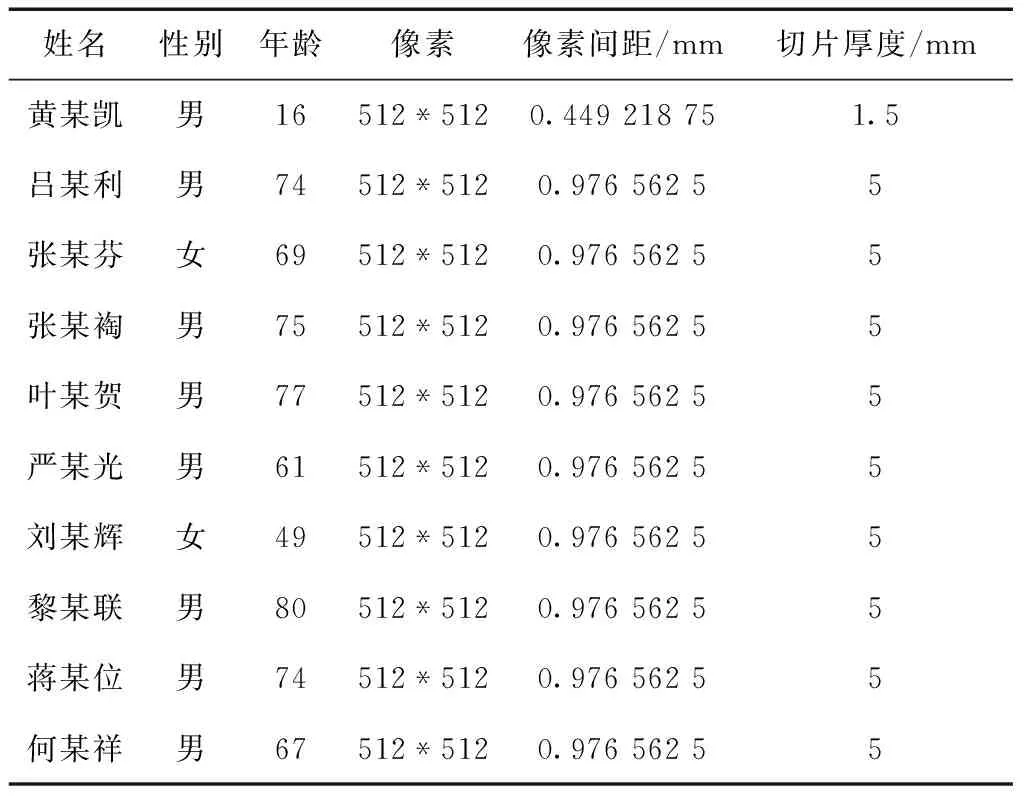
表1 脊柱CT图像序列数据

图3 CT序列图像

5.1.2 实验结果

三维模型由上一节所述的CT图像序列，通过项目组开发平台算法Marching Cubes面绘制算法构成，结果如图4所示。实际使用的三维模型是通过3D打印技术生成的三维模型。

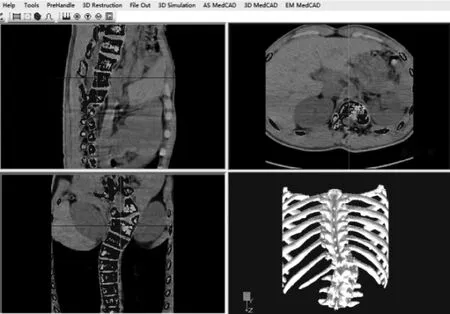
图4 三维重建平台

使用本文提出的匹配算法对摄像机中的目标进行匹配跟踪，并估计目标的三维位姿，实时渲染三维模型。实验使用10组不同的三维模型验证本文提出的算法，部分效果如图5所示。

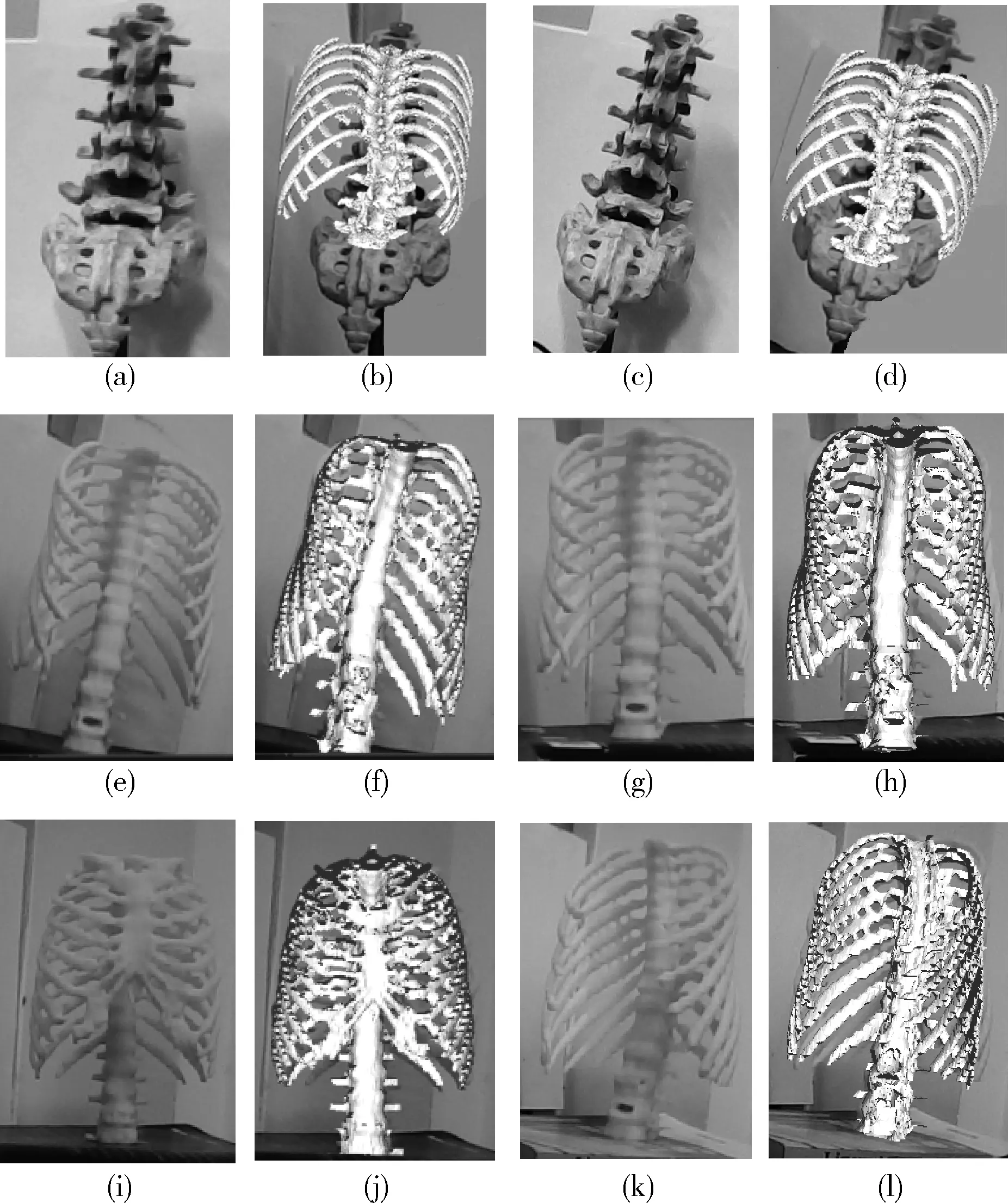
图5 现实场景目标与三维模型的匹配效果

其中图5(a)和图5(c)是使用一个假的骨骼模型来模拟现实手术中的患者，与本实验室的一个数字三维模型进行匹配，效果如图5(b)和图5(d)所示，可以实现匹配跟踪效果。

而图5(e)、图5(g)、图5(i)、图5(k)的实际模型是通过项目组平台生成的三维模型，然后将对应的三维模型通过3D打印技术打印出来，实际缩放尺寸均在133*100*200 mm上下浮动，材质是光敏树脂。将数字三维模型与对应的实体模型用于验证该算法，其匹配效果分别如图5(f)、图5(h)、图5(j)、图5(l)所示。对比结果图5中的每组图像，可以发现数字三维模型与现实的模型匹配度非常高，实验结果表明了提出算法的有效性，具体的匹配定量分析将在5.5节分析。

5.2 SURF中不同的Hessian矩阵行列式阈值对结果的分析与对比

在SURF特征的提取中，Hessian行列式阈值h是筛选特征点的主要依据，h值越大，特征点的数量越少且越稳定，鲁棒性越好。但是当特征点的数量太少时，有可能会出现局部位置特征点较少或者没有的情况，进而导致较后面的帧图像丢失该区域的匹配特征点；而特征点数量太多则会影响匹配速度，降低视频的帧率。本节针对不同的h值进行多组实验，取结果的平均值，见表2。根据表2的实验结果，画出匹配的特征点个数与h值的关系以及匹配时间与匹配的特征点个数的关系曲线，如图6、图7所示。

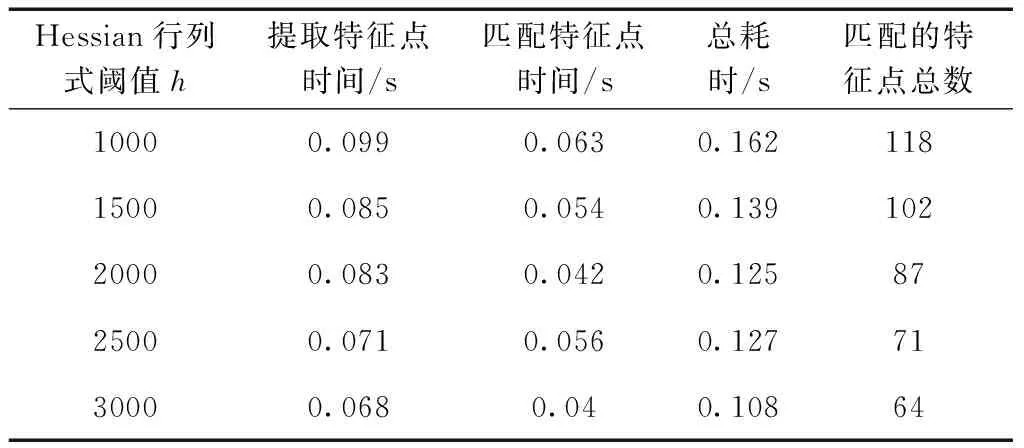
表2 不同的Hessian行列式阈值的SURF特征点匹配结果

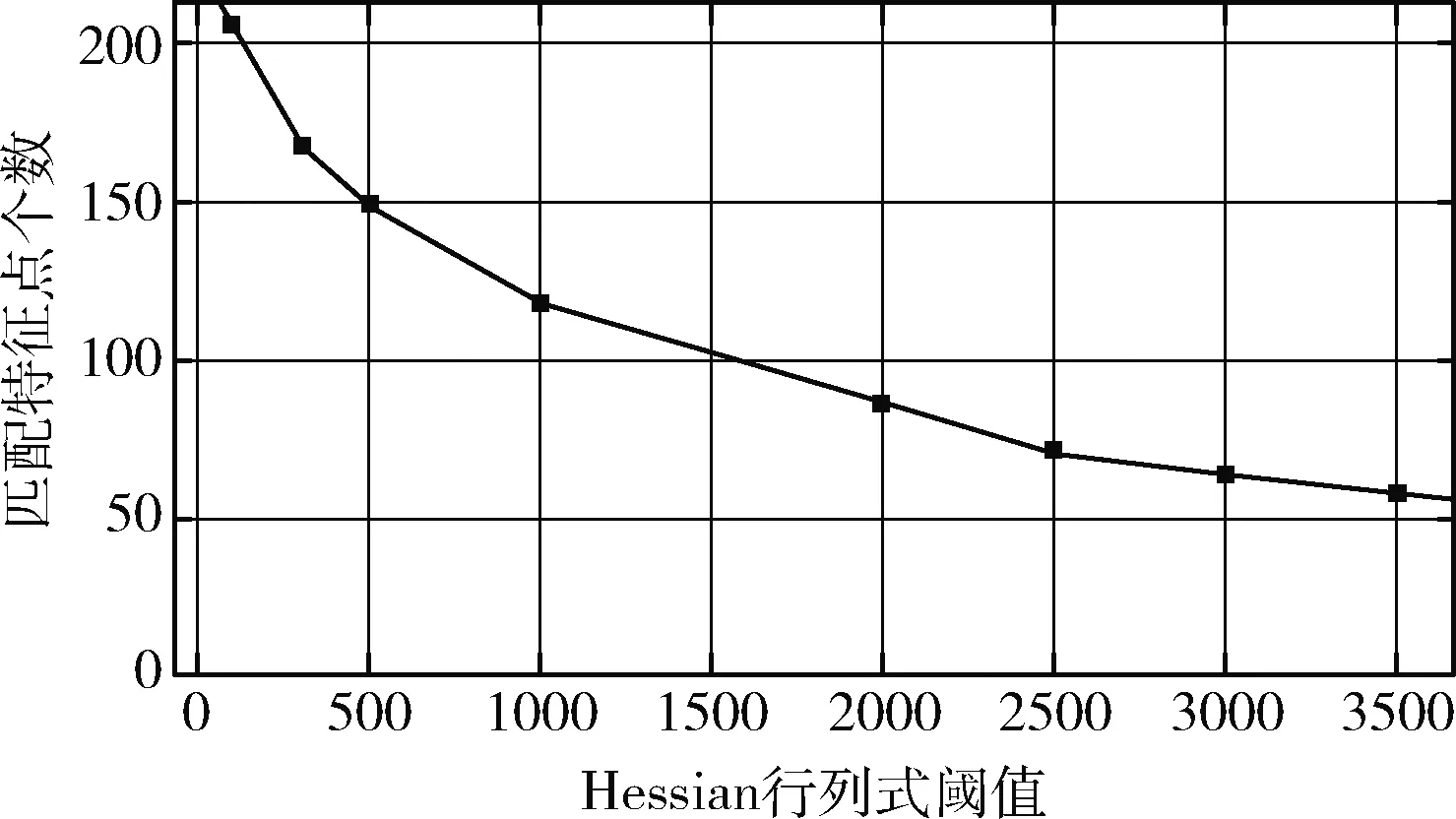
图6 匹配的特征点个数与Hessian行列式阈值的关系

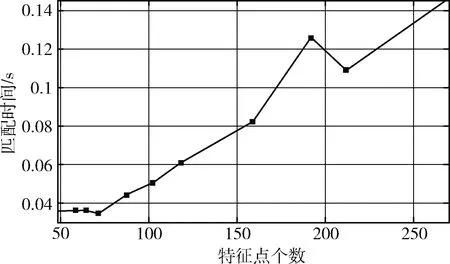
图7 匹配时间与SURF特征点个数的关系

由表2可见，以及综合图6、图7的实验结果，在理想情况下，特征点个数是随着h值的增大而减少，而匹配时间也会随着特征点个数的减少而降低。在本研究中既要保证稳定性，也要保证快速性，因此在SURF特征点的个数要从具体实验中测试，来选择适中的个数。

对比以上两图可以发现，h值为2000和2500时，特征点数量不多也不少，而且匹配速度也比较快。考虑到特征点的分布(图8)，h值为2500时，部分区域的特征点非常稀疏，从稳定性方面考虑，选择最优的h值为2000，在保证稳定性的同时不失快速性。

图8 不同的Hessian行列式阈值时SURF特征点的分布

5.3 FLANN算法最邻近距离与次邻近距离的比值阈值T对匹配结果的影响

通过特征点的最近邻距离与次近邻距离的比值来筛选错误的匹配点对。为了选出最适合的阈值T，在实验中截取两帧图像，改变阈值T，分析不同的T值对匹配结果的影响。由于FLANN算法匹配的特征点对比较多，难以一一验证每组配对点是否正确匹配，故通过特征点配对连线效果图观察有无错误配对特征点，来判断是否最优的T值。配对效果如图9所示。

图9 不同的阈值T的特征点匹配连线效果

虽然无法直接统计特征点的正确匹配率，但通过观察特征点配对连线图，可以发现随着T值减小错误的匹配对逐渐减少。当T=0.7时还存在少数的错误配对，T=0.6时已无错误配对，T小于0.6时配对的特征点数逐渐减少。在T=0.6时，使用不同的实体模型进行特征点匹配，也无错误的特征点匹配，其效果如图10所示。因此，在确保准确配对时T=0.6是最优的阈值。

图10 不同模型的特征点匹配连线效果

5.4 改进的FLANN算法匹配结果与其它算法的分析与对比

为了验证本文改进的FLANN算法的有效性及快速性，在实验中用SURF特征点的匹配时间和匹配成功率作为匹配评估指标，并且与前人改进的算法做对比实验。在同一实验环境下，并采用相同的视频图像数据，测试上述不同算法的性能指标。实验中使用10组模型，每组模型使用摄像机连续截取100帧视频图像，测试得到结果并取平均值，见表3。

表3 不同的匹配算法的性能指标

提出的算法与对比的算法都是先得到粗配对的结果，经过算法筛选才得到正确的配对，匹配成功率是通过最终成功配对的数量除以初配对的数量得到的。特征点对是否正确匹配是通过观察它们的匹配连线图来判断的。

由表3可见，文献[7]中算法的FLANN算法是直接通过最近邻与次近邻的比值来筛选最佳匹配特征点，特征点配对时进行全局特征点匹配，需要配对的特征点总数比较多，导致匹配耗时较长，且匹配正确度不高；而文献[15]算法使用RANSAC策略来剔除无效的特征点，虽提高了匹配正确度，但找出最佳的RANSAC模型需要进行多次迭代，导致匹配耗时更长。本文提出的改进FLANN算法，首先选取待匹配的局部区域(如图11每个图的左图)，然后根据上一次匹配的结果计算出两帧之间的映射关系，找出配对特征点的预测区域，最后在预测的局部区域搜索匹配特征点，因此减少大量的无用特征点匹配，比前两者的匹配速度快，而且也有较高的匹配成功率。实验结果表明了本文改进的FLANN算法对视频图像匹配的快速性。

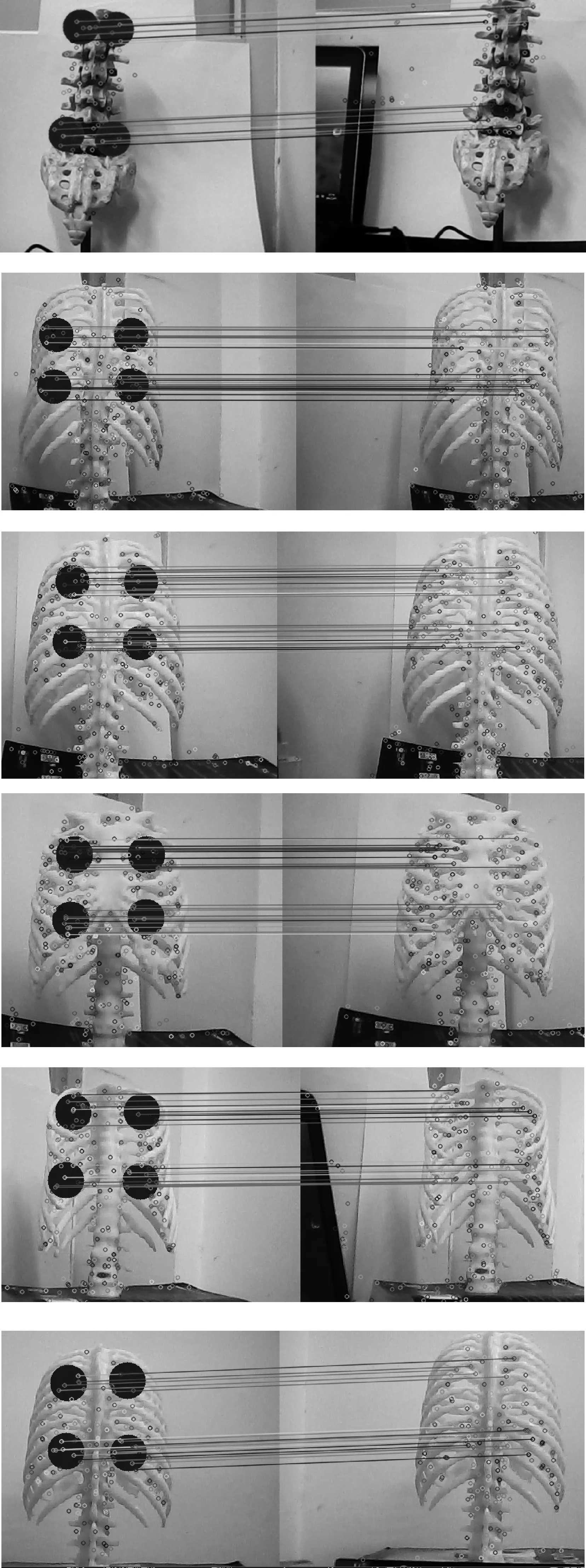
图11 改进的FLANN算法匹配

5.5 三维模型位姿估计误差的定量分析

为了进一步验证提出算法的准确性，通过三维模型位姿估计的误差来评估，采用10组不同的三维模型(数字三维模型与打印的三维模型，部分如图5(e)、5(g)、5(i)、5(k)所示)，在实验室中测量模型的真实旋转角度与平移量的平均值，通过式(9)、式(10)来计算三维模型位姿估计的误差，结果如图12所示。由于是手工测量实际的旋转平移量，其旋转角度的测量精度是±1°，平移精度是5 mm，取多个测量值的平均值作为结果。

由图12、图13可见，位姿估计的误差确实存在的，但其误差相对三维模型的尺寸来说影响不大，最终的视觉效果(图5)在可控制的范围内。减少误差主要从以下几方面考虑：①初始化选点时，二维图像目标要与三维模型准确对应；②尽量保持环境光线明亮，提高特征点匹配率；③平稳移动摄像机，保证不丢失目标；④提高摄像机的分辨率，提高特征点描述符的辨识度。

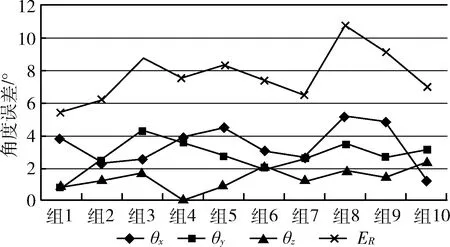
图12 位姿估计的角度误差

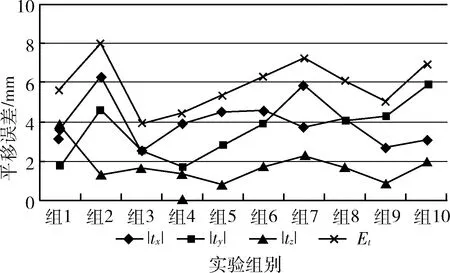
图13 位姿估计的平移量误差

6 结束语

本文针对视频图像匹配提出了基于SURF特征点的改进FLANN算法，该算法是基于上一帧的匹配结果，利用RANSAC算法的改进FLANN匹配算法，先找到特征点匹配的预测区域，然后在预测区域进行特征点搜索，避免了大量无用特征点的匹配，从而提高匹配效率。实验结果表明，本文提出的算法对视频图像匹配的稳定性及快速性。目前该算法在目标低速移动的视频匹配有良好的表现，下一步的研究主要进一步优化提出的算法，并将该算法应用到快速移动的视频图像中。