基于多特征融合的图像匹配研究

鲁家皓， 张捷， 胡国胜， 唐智

(1.上海电子信息职业技术学院，教师工作部/人事处，上海 201411；2.上海大学，机电工程与自动化学院，上海 200436；3.上海电子信息职业技术学院，通信与信息工程学院，上海 201411；4.东华大学，机械工程学院，上海 201620)

0 引言

随着多媒体技术的不断发展，每天都会产生大量的图像，图像处理技术在许多领域得到广泛的应用，如医学影像、飞行轨迹、军事等[1-3]。在图像采集过程中，由于多种因素的影响，单一幅图像无法完整描述目标的信息，为了更好地描述目标信息，可以采用多幅图像进行匹配，得到一幅更加完整的图像，因此这种图像匹配成为当前研究的重点[4-5]。

针对图像匹配问题，一些发达国家学者进行了长期的研究，提出了许多有效的图像匹配方法，图像匹配技术十分成熟，而国内图像匹配的研究时间比较晚，亦取得了相当多的成果，但是还有许多问题有待解决[6]。当前图像匹配方法可以划分为2类：一类是基于灰度信息的图像匹配方法，该类方法首先将图像转换为灰度图像，并根据灰度信息计算两幅图像之间的相似度，从而得到图像匹配结果，该类方法的图像匹配时间短，图像匹配效率高，但是图像匹配的错误点比较多，难以获得高精度的图像匹配结果[7-9];另一类方法是基于特征的图像匹配方法，首先提取图像的角点、边缘等特征，然后根据特征进行图像匹配，该类方法对图像的旋转、尺度缩放等鲁棒性强[10-12]，但是由于通常情况下图像的特征比较多，当前主要采用单一特征进行图像匹配，无法获得理想的图像匹配结果，图像匹配正确率低[13-14]。

传统图像匹配方法存在误差大、效率低等问题，为了获得理想的图像匹配结果，本文设计了基于多特征融合的图像匹配方法，在相同实验环境下，与其他方法进行了图像匹配的仿真实验。结果表明，本文方法提高了图像匹配精度，缩短了图像匹配的时间，具有十分明显的优越性。

1 多特征融合的图像匹配方法

1.1 图像的预处理

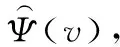
(1)

(2)

式中，a和b为收缩与平移因子。

小波分析系数的计算式为

(3)

小波分析重构形式为

(4)

图像属于离散信号，这样连续小波无法进行直接处理，为此需要对连续小波进行离散化操作:

(5)

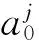
这样可以得到离散化小波分析系数的计算式为

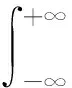
(6)

相应的离散化小波变换重构可以表示为

(7)

1.2 提取图像特征

1.2.1 LBP特征

在图像匹配过程中，需要提取特征，根据特征实现图像之间的匹配，因此特征提取十分关键，直接影响到图像匹配的结果。

当前图像匹配特征很多，局部二值模式(LBP)特征可以描述图像灰度变化特点，为此采用LBP特征进行图像匹配。图像一个像素灰度值为pf，它与邻域内N个像素点的灰度值有关联，那么该像素的LBP特征可以表示为

L=e(pf,p1,p2,…,pN)

(8)

不同像素的灰度值差别比较大，这样灰度差能够更加准确反映出图像灰度变化特点，这样LBP特征为

L=e(pf,p1-pf,p2-pf,…,pQ-pf)

(9)

通常情况下，中心像素与其他像素之间存在一定的独立性，这样有

L=e(pf)e(p1-pf,p2-pf,…,pQ-pf)

(10)

忽略中心像素点灰度值，中心像素点的LBP特征为

L≈e(p1-pf,p2-pf,…,pQ-pf)

(11)

灰度差值有正负之分，对其进行变换得到

L=e(u(p1-pf),u(p2-pf),…,u(pQ-pf))

(12)

其中：

(13)

最后图像的像素点LBP特征可以表示为

(14)

1.2.2 边缘特征

对于一幅图像f(x,y)，边缘特征也是一个十分重要的特征，采用Zernike算法提取图像的边缘特征，图像的n阶m次Zernike可以表示为

(15)

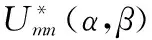
进行图像边缘检测时，通常采用Z00、Z11和Z203个阶次的Zernike不变矩，对图像f(x,y)进行旋转后得到图像f′(x,y)，那么满足条件式(16),

(16)

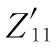
(17)

式(17)中，图像旋转角度计算式为

(18)

Zernike不变矩对图像旋转鲁棒性强，如图像幅值不变，则有

(19)

Z00、Z11和Z20的积分核函数分别为

U00=1

(20)

U11=x+jy

(21)

U20=2x2+2y2-1

(22)

旋转图像的各阶Zernike矩计算式如式(23)～(25):

(23)

(24)

(25)

由上述公式可以得到图像匹配的Zernike不变矩特征，即图像匹配的边缘特征。

1.3 图像匹配算法

由于单一LBP特征和Zernike不变矩特征无法获得理想的图像匹配结果，因此本文利用两者的优势，首先采用LBP特征进行图像粗匹配，然后采用Zernike不变矩特征进行图像精匹配，以获得理想的图像匹配结果。

1.3.1 LBP特征的图像粗匹配

对待匹配的图像进行LBP特征提取后，就可以对它们两者的LBP特征进行匹配，实现图像的粗匹配，本文选择用最近距离与次近距离比法进行粗匹配。设P1、P2为图像1、图像2的LBP特征，那么两者之间的距离计算式为

(26)

其中,Descri为LBP特征向量。

根据式(26)计算待匹配的图像的全部特征点的距离，设最近距离与次近距离比为Rod，如果Rod≤0.6，那么表示2个特征点匹配成功，不然就匹配失败。

1.3.2 边缘特征的图像精匹配

(1)采用Zernike算法提取待匹配的图像Zernike不变矩特征。

(2)根据Zernike不变矩对图像进行匹配，实现精匹配。

2 图像匹配方法性能的仿真测试

2.1 实验对象及实验环境

选择文献[13]、文献[14]和文献[15]方法，进行对比实验，共进行5次图像匹配实验，每一次匹配实验选择的匹配图像如表1所示。进行仿真实验计算机参数为Intel 4核3.0 GHz CPU，内存为32 GB，编程工具为MATLAB 2017a。

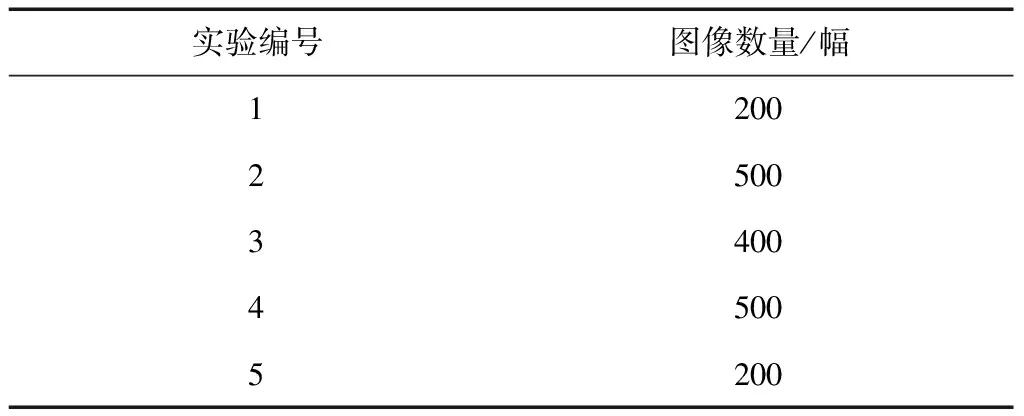
表1 每次仿真实验的图像匹配数量

2.2 实验结果与分析

统计不同方法的图像匹配时间，结果如表2所示。由表2可以看出，与其他3种方法相比，本文方法的图像匹配时间最少，加快了图像匹配速度，具有更加广泛的应用范围。

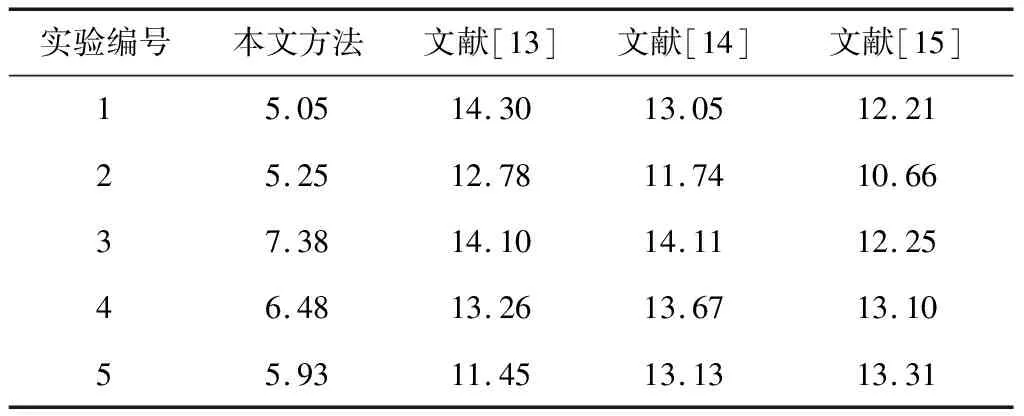
表2 图像匹配平均时间对比 单位:s

统计不同方法的图像匹配精度，结果如图1所示。由图1可以看出，与其他3种方法相比，本文方法的图像匹配精度最高，有效降低了图像匹配错误率，具有明显的优越性。

图1 不同方法匹配精度对比图

为了测试图像匹配方法的整体性能，统计不同方法的图像匹配错误率，结果如图2所示。对图2的图像匹配错误率进行分析可以看出，不同的实验，本文方法的图像匹配错误率始终小于对比方法，获得了十分理想的图像匹配结果。

图2 不同方法的图像匹配错误率

3 总结

传统图像匹配方法存在误差大、效率低等问题，为了获得理想的图像匹配结果，提出基于多特征融合的图像匹配方法。首先采集待匹配图像，并对它们进行预处理，去除一些无用的噪声，然后从图像中提取灰度特征和边缘特征，最后根据这些特征进行图像粗匹配和精匹配，并与其他方法的图像匹配仿真实验，结果表明本文方法是一种精度高、耗时少的图像匹配方法，具有更高的实际应用价值。