限制性随机试验中选择偏倚导致的一类错误率膨胀*

刘 曼 许敏怡 刘玉秀,4△ 陈文松 巩浩雯 熊殷

【提 要】 目的 探讨随机对照试验(randomized controlled trial,RCT)中应用限制性随机化方法的选择偏倚对统计检验决策的影响。方法 采用Monte-Carlo模拟比较4种常用的限制性随机化方法在不同的参数设置和猜测策略下进行统计检验时的一类错误率表现。结果 4种限制性随机化方法均会导致一类错误率超过预设的显著性水平(如5%),区组长度越小、选择效应越大,一类错误率膨胀越严重,在同等条件下,PBD的一类错误率膨胀最大,其次是BCDWIT、BUD、BSD。结论 临床试验中应用限制性随机化方法存在的潜在选择偏倚会导致一类错误率膨胀,应注意优选随机化方法并加强实施过程管理。

随机对照试验(randomized controlled trial,RCT)是评估医疗干预措施效果的金标准。随机化被认为是RCT中创建可比治疗组和减少偏倚的关键部分。限制性随机化是一类为了控制组间均衡性而设置一些限制条件的随机化方法,受到普遍欢迎[1]。然而,在开放或非盲态试验中,由于限制性随机化方法的“限制”特点,若选择和操作实施过程不当则容易产生可预测性并选择性分配受试者,进而导致选择偏倚[2]。本文通过分析该类选择偏倚对一类错误率的影响,研究其在不同随机化方法下对检验决策的影响,为随机化方法选择和偏倚防范提供参考。

原理方法

1.猜测策略

研究表明,在RCT中,若采用限制性随机化设计方法,当研究者知晓已经入组受试者的分配信息时,即使在实行了分配隐蔽并不能直接获得下一例分配组别的情况下,也往往会猜测下一例的分配,其猜测分配的行为模式一般符合Blackwell-Hodges收敛策略(BH策略)[2-3],即猜测下一例分配到当前例数较少的一组。对于两组试验,记试验组为E,对照组为C,总样本量为N,入组受试者的序号为i。假设研究者在整个试验的过程中对每一例分配都猜测,且期望试验组具有更好的效果,令gi为第i个分配的猜测分组,则

(1)

其中,di-1为前i-1名受试者中试验组和对照组的样本量之差,即di-1=NE(i-1)-NC(i-1),R服从于伯努利分布,即R～Ber(0.5),1代表试验组E,0代表对照组C。若gi=1,研究者将有意识或潜意识地选择具有有利于E组试验成功的特征变量的受试者;若gi=0,研究者将倾向选择具有不利于C组试验成功的特征变量的受试者;若gi=R,研究者没有猜测的依据,则以相同的概率随机选择第i个受试者分到E组或C组。在这种猜测策略下,研究者可以使期望的正确猜测次数最大化。

文献报道的另一种猜测策略是仅在特定情况下进行猜测[4],该策略假设研究者已知组大小及当前组内的先前分配,可得出当前受试者分配给试验组E的条件分配概率P{E},则可根据P{E}猜测下一例的分配,若P{E}超过固定的临界值q,猜测第i个受试者分配到E组。反之若P{E}小于固定的临界值1-q,猜测第i个受试者分配到C组。其中,q是人为设定的,通常≥1/2。显然该猜测策略较为复杂,似乎不够符合临床试验中研究者的猜测行为模式。因此,本研究仅采用BH猜测策略。

2.选择偏倚与检验的一类错误

在选择偏倚的影响下,临床试验中的治疗差异检验可能会出现一类错误率膨胀,例如,即使没有实际的治疗效果,组间的异质性也会导致组间疗效差异显著。Proschan[5]率先提出了收敛策略对疗效假设检验的一类错误率的影响,并基于BH策略提出如下模型。假设试验研究者偏向于试验组,并且有足够的候选受试者。即当研究者猜测下一个患者将被分配到试验组时,他会招募一名具有某些特征变量、预期结果更好的受试者;在猜测下一个受试者将被分配到对照组时,则招募一名预期结果较差的受试者;在随机猜测下一个治疗时,将会招募一名结果中等的受试者。研究者能够区分结果较好、较差或中性的受试者的程度由参数η表示, 称为选择效应。

(2)

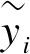
xi～N(μ1,σ2),i∈{1,…,n}

(3)

yi～N(μ2,σ2),i∈{1,…,n}

采用双侧独立两样本t检验来检验以下假设[6]:

H0:μ1=μ2↔H1:μ1≠μ2

(4)

在没有治疗效果的原假设下,我们假设研究者偏爱试验组,希望通过选择偏倚提高一类错误率,达到证明试验组优于对照组的目的。

对于二分类的响应变量,假定两组的响应结果均服从二项分布,即

xi～Binomial(n1,π1),i∈{1,…,n}

(5)

yi～Binomial(n2,π2),i∈{1,…,n}

采用Pearsonχ2检验来检验两组率是否相等。

Monte-Carlo 模拟研究

1.模拟场景参数设置

所有Monte-Carlo模拟在SAS 9.4系统环境下实现。对于连续(二分类)的响应变量,设置两处理组,每组各100例;两组的均数(成功率)均设置为0.4,选择效应(η)相应设为0.2、0.1、0.05;随机化方法选择区组随机设计(permuted block design,PBD)、大棒设计(big stick design,BSD)、带不平衡限制的偏币设计(biased coin design with imbalance tolerance,BCDWIT)、区组瓮设计(block urn design,BUD)方法;模拟研究的区组选择较小区组长度(4,8,10)和较大的区组长度(20,50,200),相应的最大容许不平衡数(maximal tolerated imbalance,MTI)取值为2、4、5、10、25;具体参数设置见表1。

表1 4种限制性随机化方法一类错误率模拟的参数设置(检验水准α=0.05)

2.模拟过程

基于各种随机化设计生成随机列表。根据生成的随机列表和研究者的选择偏好,模拟受试者进入E组或C组的分配。研究者可以根据BH猜测策略选择强、中、弱特征的受试者[6]。

对于相关参数的每个组合,重复数据生成整个过程1万次。设定检验水准α=0.05,使用t检验或χ2检验对每个生成的数据集进行分析,以检验E和C两组之间的差异,使用一类错误率评估检验决策的性能。一类错误率是指P值小于0.05的模拟数据集的比例。一类错误率偏离0.05表示存在偏倚。

为了在更现实的环境中检验选择偏倚对一类错误率的影响,我们重复进行了模拟,但改变了研究者在每种情况下都能选择具有偏好特征受试者的理想情况。即并没有足够的受试者供研究者选择,具体来说,当研究者尝试招募一名强特征受试者时,他只有50%的机会这样做。同样,研究者每次尝试招募弱特征受试者时,也只有50%的机会。若招募不到合适的受试者则招募中等强度的受试者。

结 果

1.连续响应变量的一类错误率膨胀

由图1可得,当研究者有100%的概率选择合适的受试者时,在区组随机化方法下,随着区组长度的增大,一类错误率逐渐减小,当选择效应为总效应的1/2时,除了区组长度为200的其余区组长度的一类错误率均较大,区组长度为4时,一类错误率膨胀至22%;同时,随着选择效应的减小,一类错误率也逐渐降低,但仍高于名义水平。而当研究者只有50%的概率选到合适的受试者时,其一类错误率膨胀明显减小,但在区组长度为4时,一类错误率也膨胀至10%。可见,在BH收敛策略下,无论选择效应有多小,只要有选择,就会导致一类错误率增大,且区组长度越小,一类错误率膨胀越大。

*:对应不同的研究者猜测情况,guess=50%表示研究者有50%的概率选到心仪的受试者,guess=100%表示研究者有100%的概率选到合适的受试者

各类情况下的BUD的一类错误率的变化趋势与PBD大致相同,即随着区组长度的增加而减小(图1),但该趋势仅在区组长度较小(小于10)时较为明显。在100%选择的理想情况下,区组长度为4时,一类错误率最大为12%。当受试者人数有限无法供研究者任意选择时,各区组长度下的一类错误率大致相同,一类错误率在区组长度为4时较大(8%)。

BSD的一类错误率随着MTI的增加而降低(图2),当受试者足够供研究者选择时,MTI为2,选择效应为0.2下的一类错误率为11%,当MTI大于4时,一类错误率明显降低。而当受试者人数有限无法供研究者随意选择时,一类错误率的情况有所好转,选择效应较大、MTI较小时,一类错误率较大。

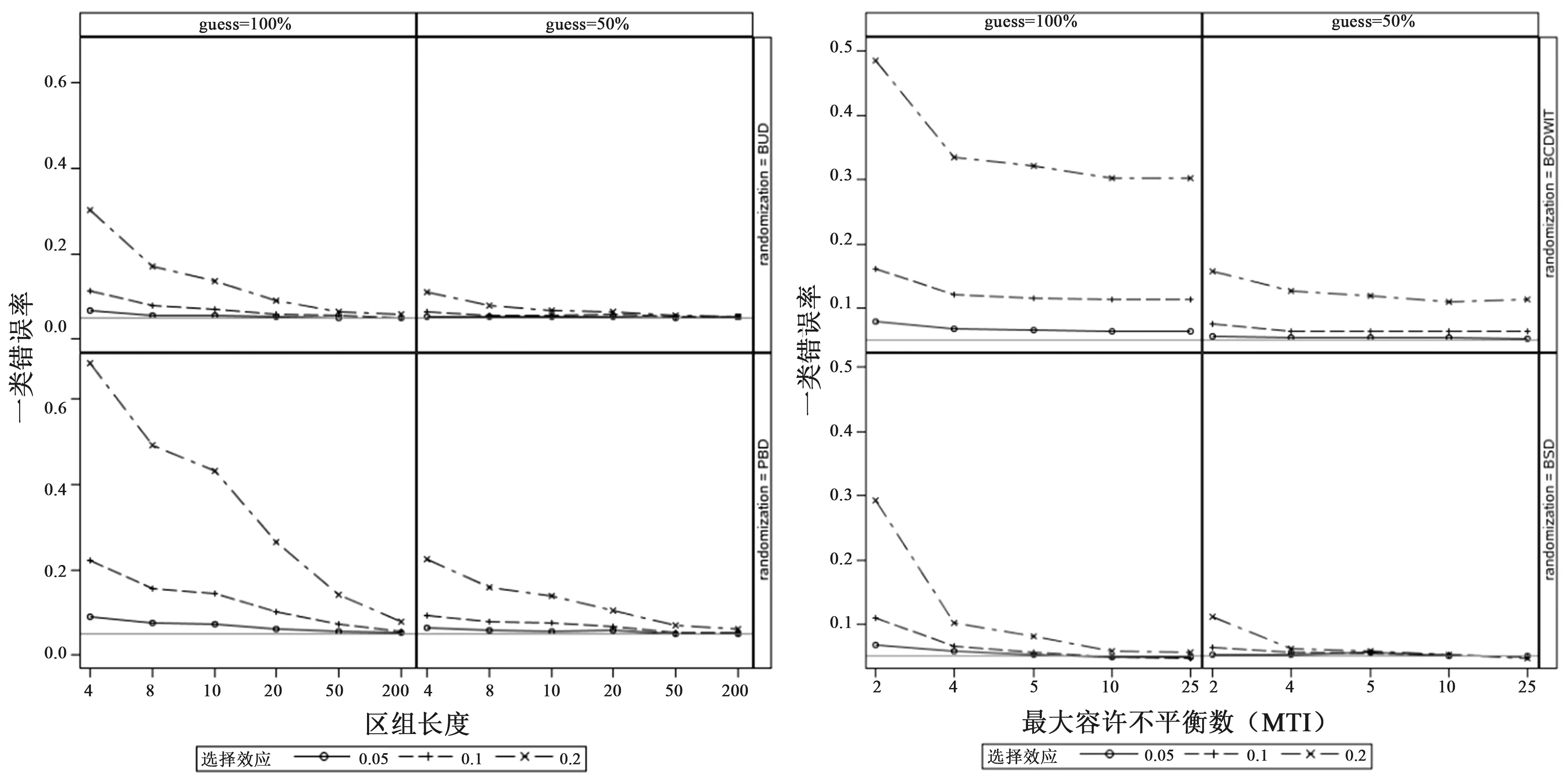
注:对应不同的研究者猜测情况,guess=50%表示研究者有50%的概率选到心仪的受试者,guess=100%表示研究者有100%的概率选到合适的受试者

BCDWIT是BSD和偏币设计的综合(图2),当选择效应较大时,一类错误率随着MTI的增加而减小,选择效应为0.2、MTI为2时,一类错误率膨胀至15%;当选择效应较小(0.05)时,一类错误率降低到名义水平;而当受试者人数有限无法供研究者任意选择时(guess=50%),一类错误率明显降低,其趋势与100%猜测的情况大致相同。

2.分类响应变量的一类错误率膨胀

在二分类响应变量情况下,一类错误率随区组长度和选择效应的变化趋势与连续变量大致相同,但其值均明显增大,在100%猜测的区组设计下,区组长度为4,选择效应为总效应的1/2时,一类错误率竟膨胀至0.68,50%猜测的情况下,也膨胀至0.22,BUD、BSD的一类错误率虽较PBD小,但也膨胀至30%。

为了方便比较4种随机化设计的一类错误率膨胀,我们列举了区组长度为4或MTI为2的参数设置下对应的一类错误率模拟结果(表2)。综合来看,PBD在各种选择效应和研究者猜测情况下,都有一类错误率膨胀,且大都高于其他几种方法,其次是BCDWIT,BCDWIT的一类错误率膨胀虽较前者小,但仍高于名义水平,一类错误率膨胀最小的是BSD,在选择效应为0.2时,一类错误率为0.1092;因此,在同一参数设置下,各随机化设计的一类错误率膨胀顺序为PBD>BCDWIT>BUD>BSD。

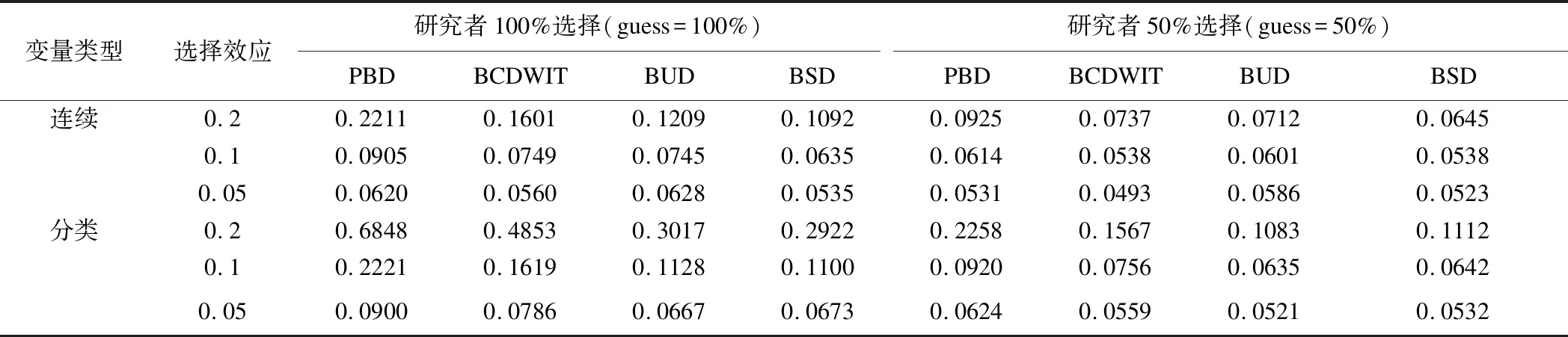
表2 MTI为2(区组长度为4)时几种限制性随机化方法的一类错误率

讨 论

本文分析了限制性随机化方法下因选择受试者导致的选择偏倚,并通过Monte-Carlo模拟比较了4种限制性随机化方法在不同的参数设置和猜测策略下的一类错误率表现。模拟研究发现,该种选择偏倚会导致一类错误率超过预定的显著性水平,在同一MTI下,PBD的一类错误率膨胀最大,其次是BCDWIT、BUD、BSD。当然,若当受试者人数有限无法供研究者任意选择时,一类错误率膨胀会减轻。这一结果从另一角度也印证了前人对上述4种限制性随机化方法性能研究的结论[5,7]。

其实,有关选择偏倚对临床试验一类错误率膨胀的影响早有研究,对于平行组设计中的正态分布结果数据,Proschan[5]使用Z检验进行分析,并推导了随机分配规则(RAR)下的一类错误率膨胀公式。Kennes等人[6]继续这项工作,模拟了PBD的一类错误率膨胀情况,并进一步扩展到多中心试验[8]。但以往的研究多考虑正态分布变量,随机化方法也仅限于PBD,本研究在此基础上探讨了多种限制性随机化方法的一类错误率膨胀行为,并考虑了二分类结果变量的情形。结果发现二分类结果变量更易受到这种选择偏倚的影响,其一类错误率膨胀更大。

尽管我们的模拟也表明在4种限制性随机化方法中,PBD最易导致一类错误率膨胀,但该方法因操作上的简便性仍广为应用。2015年Lin等报道,在NEJM、Lancet、JAMA期刊上发表的RCT文献中有82%采用了区组随机化方法[9]。我们对2018年发表在NEJM上全年的RCT论著进行了分析发现,分层区组随机化(72.65%)最多,其次为区组随机化(11.11%)、最小化(9.40%)、简单随机化(4.27%)[1]。但区组设计方法随机性能低下已有明确研究结论,2006年,Berger甚至强烈建议不使用区组设计[10]。毋庸置疑,人们在现实临床试验中偏爱选择PBD方法的现状亟待关注和改善。近年有些学者对限制性随机化方法下选择偏倚的检测和校正进行了探讨[11-12],但远未解决实际应用问题,应需今后进一步加强方法学研究及应用。