体外诊断试验定量项目一致性评估的统计分析方法探讨

黄雪梅 谭春艳 周 莹 杨霞芳 王 岩 莫志江△

【提 要】 目的 以统计软件为工具,用实例形式探讨体外诊断试验定量项目一致性评估的统计分析方法。方法 对于目前无临床认可界值的项目,我们建议以室内质控(intermal quality control,IQC)、生物变异数据库、室间质评(extermal quality assessment,EQA)和CLIA′88(clinical laboratory improvement amendments of 1988)作为参考;利用SPSS 26.0和MedCalc 20.0处理数据,包括样本量估算模块,Frequencies(频率)模块,单样本符号秩和检验和回归分析。结果 通过参考IQC、EQA和CLIA′88解决目前大多数定量项目无临床一致性界值可用的问题;MedCalc的Bland-Altman plot和 SPSS的 Frequencies(频率)模块可提供一致性界限(limits of agreement,LoA)和容许区间(tolerance interval);MedCalc单样本符号秩和检验可提供完全符合EP09-A3要求的偏倚分析结果;SPSS的回归模块可用于评估医学决定水平处的偏倚和LoA。结论 本文的统计分析方法可提供符合规范要求的体外诊断试验定量项目一致性分析结果。

临床实验室体外诊断试验定量项目的一致性评估常见于临床试验和方法学比对(包括多套检测系统的比对)等工作中,可参考的最新指南主要为《临床实验室总分析误差评估》(EP21-A)和《用患者样本进行方法比对及偏倚评估:批准指南,第三版》(EP09-A3)等,但两者的应用不同:前者用于评估总误差(系统误差和随机误差之和),也就是准确度(accuracy)[1];后者用于评估系统误差,也称偏倚(bias)或正确度(trueness)[2],两者常被混淆。国家药监局发布的《体外诊断试剂临床试验指导原则(2021年第72号)》(以下简称《指导原则》)要求同时评估总误差和系统误差。

实际工作中,我们发现存在一些问题。一是缺乏一致性评判标准的预先确定,付央[3]等收集的含有Blank-Altman法的98份体外诊断试剂注册申报资料,无一事先确定临床认可界值(或称临床意义界值、临床界值)。二是缺乏样本量估算。三是统计方法的应用不充分,甚至失当,不能完全满足一致性评估的需要,如方法学比对未给出偏倚的95%置信区间(95% confidence interval,95%CI),体外诊断试剂临床试验仅评估系统误差,Bland-Altman法的应用不规范等。

EP21-A和EP09-A3介绍的统计方法均为手工计算,涉及大量统计学概念和复杂难懂的公式,难以完全正确解读和执行。本文的实例分析完全符合EP21-A 、EP09-A3和《指导原则》的规范,统计结果均出自SPSS和MedCalc软件,期望能有助于高效、规范地进行体外诊断试验定量项目的一致性评价。

材料与方法

1.实例数据来源

本研究数据来源于桂林优利特医疗电子有限公司于2011年3月至2011年8月在中心1(广西壮族自治区人民医院,对照仪器1:Sysmex XE-2100全自动血细胞分析仪)和中心2(广西医科大学附属医院,对照仪器2:Coulter LH750全自动血细胞分析仪)完成的URIT-5500五分类全自动血细胞分析仪临床试验,本文仅摘其中的血红蛋白(hemoglobin,HGB)项目作实例分析演示,见表1。

表1 试验仪器与两种对照仪器在血红蛋白(HGB)项目中的单次检测结果(g/L)

2. 数据处理

采用专业统计软件SPSS 26.0和MedCalc 20.0,两者都有一些对方缺失的功能,可以互为补充,涉及的统计模型见下文。

数据分析和结果

本文按照表1的结果用以下公式定义一些重要术语:

设xi为对照仪器的检测结果,yi为试验仪器的检测结果(i为样本序号,i=1,2,…,n,n为样本量),按以下公式定义本文术语:

检测均值=(yi+xi)/2

(1)

di(difference,差值)=试验仪器检测值-对照仪器检测值=yi-xi

(2)

di%(difference%,差值%,相对差值)=100×(yi-xi)/xi

(3)

di%(difference%,差值%,相对差值)=100×(yi-xi)/检测均值(仅限于图2)

(4)

(5)

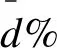
(6)

EP21-A将差异值(差值或差值%)的95%CI分布范围定义为总分析误差(total analytical error),对应于Bland-Altman法的LoA,本文一律统称为LoA。EP21-A将总分析误差限(total analytical error limits)定义为分析总误差的最大允许界限,对应于Bland-Altman法的最大允许误差(maximum allowed difference)和临床实验室的允许总误差(allowed total errors,TEa), 本文一律统称为TEa。

根据公式(5)和公式(6),偏倚和偏倚%分别由差值均值和差值%的均值来刻画,若正态分布不成立(尤其是偏态),则改用中位数代替。

1. 允许总误差和临床认可界值的确定

EP21-A要求预先确定TEa以评判试验的LoA是否满足要求。应依据研究目的和行业标准而定,还可参考室内质控(IQC)、生物变异数据库、卫生部临床检验中心室间质评(EQA)和CLIA′88等标准。临床认可界值△也是可参考的标准,指的是该差异对临床的诊断和治疗影响很小。当不存在业内公认的△值时,需有临床专家预先参与确定,因具有一定的主观性,不可在取得试验结果后量身定制。HGB项目多个一致性标准见表2。

表2 HGB项目的多个标准的允许总误差(TEa)

IQC的允许波动范围反映了某检验系统的日常正常波动,若LoA处于这一范围内,可以认定该差异犹如源自于同一检验系统,两者的结果可视为等同,属于最优的试验结果;若能达到EQA或CLIA′88标准,表明LoA处于目前技术能力范围内,结果可接受;生物变异数据库反映个体内和个体间的波动情况,LoA若能满足该标准表明可以接受。大多数临床检验项目不存在表2的所有标准。

按总误差来源,TEa从小至大排序应为IQC≤(生物变异数据库,EQA,CLIA′88)≤Δ,IQC应最小,否则不应被采纳,应尽量采用知名大厂的IQC标准以满足这一排序。因此,在无临床认可界值Δ的情况,可用排序在前的标准予以替代。

《指导原则》要求LoA在临床认可界值内,但未具体阐明如何确定,也难以找到有使用价值的相关文献,因此这一步骤在实际工作中鲜有被执行,尽管这是判断两个方法是否一致的关键。

EP09-A3的方法学比对仅涉及偏倚,一般取1/2TEa,常用1/2 CLIA′88标准。

2. 样本量估算

《指导原则》虽然要求进行样本量估算,但仅提供了定性而没有定量方法的估算公式。按照EP21-A,总误差在一致性评估中最重要[1],因此本文将其作为样本量估算的指标,可根据研发阶段数据或文献等信息进行估算。

若差值或差值%呈非正态分布(尤其是偏态分布),应该使用非参数法,此时我们建议至少100例,达到200例以上可以取得较为稳定的95%容许区间(定义见下文),具体理由见下文讨论部分。

若差值或差值%呈正态分布,则MedCalc的Bland-Altman样本量模块是很好的专项工具。本文前期数据呈近似正态分布,以CLIA′88的TEa(±7%)作为临床认可界值,结果见表3。

表3 Bland-Altman图最小样本量估算结果(α=0.05,β=0.2)

一般而言,低浓度段的数据有可能变异较大(尤其是差值%),因此表3增加了一个≤80 g/L的低浓度段。此外,±7%折算为差值时,按表2质控物的低值58 g/L折算以取得保守的样本量估算值。根据表3,当样本量不低于56时,可以得出与研发阶段相近的结果。

3. 利用差异图评估总误差和偏倚

EP21-A和EP09-A3的差异图(difference plot)包括差值图和差值%图,用于评估总误差和偏倚。Bland-Altman图假定差值和差值%(统称差异值)服从正态分布[1],是差异图的特例,也是目前最常用和最被认可的一致性评价方法[4-5]。

对于差值和差值%,参数法采用MedCalc 的Bland-Altman模块量化,非参数法采用SPSS的Frequencies模块量化。若正态分布成立,两者的结果将会十分接近,本文一并列入表4以便比较。

表4 HGB差值和差值%的分析结果

本文引入Frequencies模块用于非参数法的一致性评估,其通过Bootstrap法估算表4统计量的95%CI以供评估抽样误差的波动范围。(-5.0505%, 3.8462%)为95%容许区间(95% tolerance interval,95%TI),是一个EP21-A术语,源自于LoA下限的95%CI下限(-5.0505%)、上限的95%CI上限(3.8462%)。

MedCalc可直接生成Bland-Altman差异图(图1和图2),必须目视检查图形的数据点分布情况。只有差异值在整个横轴上分布基本相同,散布成水平条带状的恒定分布时,表4对应结果的正确性方可保证,此时上下两条虚线水平平行,即全图有相同的LoA值。

图1 HGB的Bland-Altman差值图

图2 HGB的Bland-Altman差值%图

图1大致呈恒定分布,但沿着横轴,差值的分散程度大致随着HGB均值增加而增大。图2相对于图1更符合恒定分布,故采用其对应的量化结果,且将±7%的TEa(CLIA′88标准)加入图中以便于结果判读。图1和图2都没有离群值存在的迹象。

图2的TEa(±7%)完全包含LoA(-3.3%, 4.5%)和95%TI(左侧相交且垂直于LoA的误差线),因此该项目两个方法的总误差足够小,可满足临床使用需求。参考表4,即使按照非参数的结果判读,前述结论仍未改变。此外,由于两个中心的数据点相互混杂,表明结果一致,无须担心中心效应问题。

《指导原则》没有提及95%TI,只要求LoA在临床认可界值内,因此临床试验中95%TI超越临床认可界值不归为试验失败。如未超越,则对结果符合要求更具信心。

至此,以上结果已足够支持试验仪器用于临床检验日常工作,理论上其他结果(如回归分析等)并非必须[2],这是因为以上LoA为对整个检测范围内总误差的评估结果,包含了一致性评价的所有要素。

表4包含偏倚结果。差值%均值(偏倚%)0.6418%(0.1270%, 1.1566%)虽不包含0值,但在LoA范围内占比很小,属轻微偏倚。若按差值%中位数1.1634%(0%～1.3890%),结果相近。若以1/2 CLIA′88(±3.5%)作为最大可接受偏倚,按EP09-A3规则判断(由优至差依次分为A至E五档),前者为B,后者为A,均属可接受[2]。

若差异图不呈恒定分布而呈EP09-A3介绍的线性变化,则以上量化分析不适用,可采用SPSS的线性回归拟合差异值与浓度的函数关系[2,6],可让其输出偏倚及其95%CI,以及LoA。若呈非线性变化,则本文所有的量化方法(包括下文的单样本符号秩和检验、单样本t检验和回归模型)均不适用,我们推荐使用SPSS含11个模型的曲线拟合模块(curve estimation)拟合差异值与浓度的函数关系,选择最佳模型后可让其输出偏倚和LoA。这两种情况下,没有全图相同的LoA,也无法输出95%TI。

4. 利用单样本t检验和单样本符号秩和检验评估偏倚

单样本符号秩和检验是单样本t检验的非参数版,MedCalc在该模型中还集成了单样本t检验,是量化图1和图2偏倚的有力工具,分析结果见表5。

表5 MedCalc单样本符号秩和检验对差值和差值%的偏倚分析结果

表5包含了EP09-A3对差值图和差值%图进行偏倚量化的所有结果,且与表4的偏倚结果十分接近。一些文献仅做配对t检验,仅等效于差值的单样本t检验,且不报告其95%CI,应用价值大减。

5. 利用回归分析评估偏倚和总误差

表6 HGB项目的回归结果汇总

EP09-A3将表6与表5(或表4)的结果进行比较以证实这些模型的可信性,从中选出最佳模型。表5的偏倚%为0.6418%(0.1270%, 1.1566%),对应的回归方程斜率应接近于1+0.6418%=1.0064(95%CI:1+0.1270%=1.0013至1+1.1566%=1.0116)。截距应接近于表5的偏倚0.8167(0.2371, 1.3962)。因此,表6的WLS斜率1.0057(0.9945, 1.0169)、截距0.0729(-0.9654, 1.1112)最为接近,为最佳模型。

图1的差值多少有些呈喇叭型分布,因此加权回归和Passing &Bablok回归都是合理的选择。鉴于差值也大致呈恒定分布,因此使用普通线性回归和Deming回归同样合理,这就是表6各个模型的结果都较为接近的原因。检查差异图和(xi, yi)散点图可为选择合适的回归模型提供一定参考(详见EP09-A3,本文不再赘述),但通常不能确定唯一的模型,当结果不吻合时,需更换模型。

在选择回归模型时,我们建议应侧重考虑医学决定水平(Xc)、危急值和参考限,让回归线尽可能穿过或逼近这些临床关注值的数据点,以在这些特殊浓度处能产生更为准确的模型估值,也就能更准确地评估试验仪器在这些浓度处的一致性。例如,有些项目的Xc位于低浓度范围内,若表5确定的差值均值接近于0,则选择的回归模型截距也应接近于0,起码相对于Xc值可以忽略不计。否则,回归线就会偏离低浓度数据,产生不符合低浓度实际情况的模型估值。当然,这可能会以牺牲中、高浓度的准确性为代价,但此时临床关注值不在这些浓度范围内,这是可以接受的。

表7 WLS医学决定水平处(Xc)的偏倚估值和相对偏倚估值

表8 WLS医学决定水平处(Xc)的LoA

显然,表7和表8分别吻合表5和表4所对应的结果。对医学决定水平处(Xc)检测结果的一致性评估,一直以来都是通过偏倚结果来衡量,通过表8提供的LoA,可以增加一个评估指标。

虽然回归分析在偏倚量化中的应用要广泛得多,但表5的结果也凸显了差值和差值%偏倚量化的重要性,不但在替换性研究中(临床实验室引进新方法、新仪器、新试剂等)起决定性作用,且可用于证实回归结果的可信性,虽然其重要性已被EP21-A和P09-A3提及,但仍容易被忽视。

讨 论

1. 非参数法的样本量考虑

我们未能找到明确的样本量估算方法,但可从95%TI的角度考虑。EP21-A用于非参数方法示例分析的数据(低密度脂蛋白项)样本量为100,按照其附录B的TI表[1],这是LoA设定包含至少95%差异值的条件下,取得双侧TI置信水平至少为95%的几乎最低样本量,此时95%TI的下限和上限分别由该样本的最小值和最大值构成,实际置信水平为96.29%。显然,本文HGB实例样本量为60,其非参数法的95%TI当然是由最小值和最大值构成,TI表显示双侧TI实际置信水平肯定低于90%。

按照EP21-A附录B的统计学表格,当样本量达到200时,95%TI的下限和上限不再由样本的最小值和最大值分别构成,基本可摆脱样本量不足的限制。随着样本量的进一步增加,95%TI更趋于稳定。因此Bootstrap法虽被推荐用于小样本量研究[7],但在体外诊断试剂的一致性研究中存在一定限制。

综上,对于非参数方法,我们建议至少100例,为取得较为稳定的95%TI,需达到200例以上。

2. 统计方法选择的适用性

体外诊断试剂临床试验的考核试剂(仪器、检测系统等),从未在临床上应用,其准确性未知,因此主要评估差异图(包括Blank-Altman图)的总误差(LoA)。此外,还可以差异图和回归分析的偏倚结果作为补充。

若使用Blank-Altman法计算LoA或偏倚(尤其是LoA),需要确保差异值为正态或近似正态分布,可通过目视检查SPSS的P-P图或直方图(histogram)等图形方法加以确认,统计学检验法(如单样本Kolmogorov-Smirnov检验等)因过于敏感(大样本尤为如此),结果具有误导性而不予推荐。若差异值不满足正态要求,可用Frequencies模块提供一个不依赖正态分布、对离群值不敏感的非参数结果。

若仅需要按EP09-A3评估偏倚,可以使用MedCalc单样本符号秩和检验和回归分析。

本文所使用的统计模型都经过分析EP21-A和EP09-A3的相关范例进行验证,得到了完全相同或相近的结果。

3. 图形检查的重要性

图形检查对于一致性评估结果的正确性十分重要,但常被忽略。正是通过图形检查发现差值%相对于差值更具恒定分布,而只有恒定分布才能确定一个全图一致的LoA。此外,图形检查也为筛选回归模型提供依据,可参考EP09-A3对恒定SD(恒定标准差)、恒定CV(恒定变异系数)和混合变异(mixed variability)等图形的描述[2]。

图形检查的另一个任务为探查可能的离群值。线性回归(以及相关分析)以最小二乘法拟合模型,离群值(outlier),尤其是极端值(extreme value)将可能扭曲相关系数和回归系数,这些异常数据在散点图上远离数据主体,一般可通过目视检查初步确定,然后利用MedCalc软件的离群值探测模块(outlier detection)的ESD检验(generalized extreme studentized deviate)予以确认[1-2],必要时利用SPSS的箱型图(boxplot)鉴别离群值(1.5～3倍四分位间距)和极端值(3倍以上四分位间距)[8]。按照CLSI系列文件,离群值除非出自错误结果,否则不可排除在数据分析之外,此时应采用非参数模型分析数据[1-2]。

4. 数据转换的适用性

对于差异值不符合正态分布,尤其是右偏数据,多建议进行对数转换[3,9-10],但转换后所得到的算术均值反对数后为几何均值,对称的LoA反对数后不再对称,其覆盖范围不能完全反映原始数据的范围,将其与原始数据对称的TEa(如±7%)比较显然不再合适。

对数转换仅适用于定有专门标准的项目。例如,《以药动学参数为终点评价指标的化学药物仿制药人体生物等效性研究技术指导原则2016版》规定生物等效标准为(80%, 125%),上下限并未在100%的左右对称,而是下限log(80%)=-0.09691和上限log(125%)=0.0969在0值(即几何均值100%的对数值)左右对称,以适应数据分析规定的对数转换。EP09-A3亦强调数据转换后回归分析的斜率不可再与原始数据的可接受偏倚比较[2]。此时,使用非参数法以避免转换数据是必需的。