基于段路由的IPv6网络优化算法

刘 威，黄 萍，孙凤杰

(1.深圳供电局有限公司 信息中心，广东 深圳 518000；2.华北电力大学 电气与电子工程学院，北京 102206)

0 引 言

流量工程(TE)被网络运营商广泛应用于提高网络性能和效率[1,2]。软件定义网络(SDN)为流量工程提供了一种更灵活的方法[3]。网络运营商可以通过集中式控制器在控制平面上实现路由算法或策略，灵活地将任意比例的流量分流到SDN交换机的任何出站链路，突破了最短路径路由限制。在SDN中实现TE通常需要大量的流表项，因为业务路径上的每个交换机都必须有一个对应的流条目。当需求量很大时，商品交换机的流量输入能力往往不足。段路由(SR)[4,5]是一种新兴的源路由范式。SR不需要路径信令，每流状态只在入口SR节点维护，所以它具有可伸缩性和灵活性。然而，从传统的IP网络迁移到完整的SR网络对于Internet服务提供商(ISP)网络来说存在许多挑战。首先，由于现有网络中的传统路由器并支持SR，所以可能会被新设备取代。其次，虽然软件升级可以使一些高级路由器运行SR，但大规模升级所有网络设备仍可能导致网络服务不稳定甚至网络中断。所以在IP网络中部分部署SR节点的混合SR网络是一种可能的过渡网络场景。

混合IP/SR网络设计的一个关键问题是如何通过较少的SR节点来获得与完整SR网络几乎相同的TE性能，因为SR节点的部署越少，网络升级就越容易。目前，基于混合IP/SR网络的TE研究较少。并且目前的研究不能充分发挥IP/SRv6网络的TE能力。

在本文中，针对部分部署的SRv6网络提出了一种TE算法(ST)，以最小化网络的最大链路利用率为目标。本文的主要创新如下：①针对分散部署IP/SRv6网络中的SR-TE问题，利用SRv6与普通IPv6节点之间的无缝互操作性，放宽SRD的限制，并假设支持SRv6的节点可能不构成原始网络拓扑的任何连通子图。它可以提供更大的灵活性。②ST算法不仅考虑了SR节点的部署，而且考虑了链路权重的设置。该方法利用IGP的TE能力来弥补部分部署SR网络中TE能力的不足。③考虑到流量变化，将ST分为两个阶段：离线网络设计和在线路由优化。在离线阶段，确定了网络运行时不易改变的链路权值设置和SR节点部署，并提出了以一天内历史流量矩阵(TMs)上的重心作为代表流量矩阵(TM)的初步设想。在在线阶段，用线性规划来确定每一个新TM的段列表。

1 问题描述

1.1 网络场景

在提出的IP/SRv6混合网络场景中，所有节点都运行传统的网络协议栈并支持IPv6和OSPFv3协议，而其中只有一部分节点支持SRv6。假设支持SR的节点分散部署，这意味着它们可能不构成原始网络拓扑的任何连通子图。每个IPv6节点将为任何前缀维护一个FIB(forward information base)条目，无论前缀是否代表一个段[5]。因此，可以通过不支持SR的节点将数据包转发给拥有SID的节点，而且OSPFv3支持处理和洪泛未知的LSA类型[6]，因此SRv6控制消息可以通过非SRv6节点进行交换[7,8]。

图1显示了混合IP/SRv6网络的示例。在这种拓扑中，节点B、节点D和节点F支持SRv6，其它节点是传统的IPv6节点。请注意，SR节点(B、D和F)不是直接连接的。节点ID用于表示它们的SID和相应的IPv6地址。从节点A发送并定向到节点G的分组遵循最短路径直到到达节点B，即入口SR节点。从这里开始，包由SRv6路由(用虚线表示)。节点B有两个选择：①它可以在IPv6报头和有效载荷之间插入一个带有Clear标志的SRH，并且由于Clear标志，SRH将在节点F处被删除；②它可以使用SRH将接收到的包封装在外部IPv6报头中，并且包将在节点F处解封装[9]。在图1中展示了封装方式。节点B将数据包封装在外部IPv6报头中，SRH指定段列表 〈D,F〉。数据包通过节点C，沿着从节点B到节点D的最短路径到达节点D。节点C不会检查或更改SRH，因为它不是外部IPv6报头的DA字段中标识的目标节点。它根据IPv6的DA字段将数据包转发给D。节点D减小SRH的Segment Left字段，并将外部IPv6的DA字段设置为F。然后数据包通过节点E到达节点F，即出口SR节点。根据OSPF协议，数据包在节点F处解封装，并沿最短路径转发到节点G。

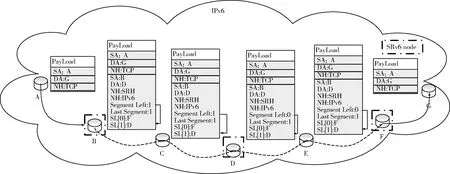
图1 一个混合IP/SRv6网络

根据上述描述，部分部署的SRv6网络中的路由有3个阶段：①从源节点s(l)到入口SR节点；②从SR节点到另一个SR节点；③从出口SR节点(如果不涉及SR路由，则为s(l))到目的节点t(l)。一条完整的流量路径可以看作是由3种类型的子路径组成：

(1)从s(l)到t(l)的最短路径在从s(l)到SR节点的最短路径上，对应于路由的第一阶段。流量从这种子路径开始，通过OSPF协议路由，直到到达SR节点；

(2)任意两个SR节点之间的最短路径，对应到路由的第二阶段。包由SR在这类子路径上路由，每个子路径代表一个节点段；

(3)从SR节点(或s(l))到t(l)的最短路径，对应于路由的第三阶段。数据包通过OSPF协议路由，通过这种最短路径到达目的节点。

1.2 问题表述

这里的TE问题可以表述如式(1)～式(12)所示

minUmax

(1)

式(1)是问题的目标函数。在这里打算尽量减少网络的最大链路利用率。它是SR-TE[1,10]中的一个经典目标，它均衡地提高了链路的利用效率

(2)

在式(2)中，c(e)以及后面的w(e)代表链路e的头/尾的容量和权重，d(l)是需求l的目标节点。式(2)限制了链路所承载的业务量不能超过其容量

(3)

(4)

式(3)表示变量f和g之间的关系。式(4)是流量守恒约束，s(l),t(l)表示为需求l的流量

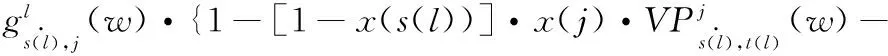
x(s(l))·x(j)}=0, ∀l∈L,j∈V{t(l)}

(5)

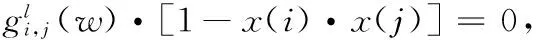
∀l∈L,i∈V{s(l)},j∈V{t(l)}

(6)

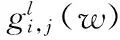
(7)

式(7)约束为i不是s(l)时,gli,t(l)(w)必须等于0，除非i是SR节点

(8)

在这里1的约束为任意节点到它自身，任何节点到s(l)，以及t(l)到任何节点，g都必须等于0

(9)

式(9)为SR部署比约束

i,j∈V,e∈E

(10)

(11)

1≤w(e)≤216-1∧w(e)∈∀e∈E

(12)

式(10)～式(12)是一些琐碎的数值约束。因为w也是这个公式中的一个变量，所以它不能用优化求解器来求解。

1.3 问题复杂性

当OSPF权重设置固定且SR_Ratio=1时，问题被简化为MCF问题，并且可以在多项式时间内解决[11]。然而，在这里只有某些节点具有SR功能。因此，需要确定OSPF链路权重来优化Umax，这增加了问题的复杂性。OSPF权重设置问题被验证是NP难度问题[12]。OSPF权重设置问题可以在多项式时间内归结为本文的问题，因为在SR_Ratio设置为0的情况下解决这个问题可以得到相应OSPF权重设置问题的解决方案。所以整个问题的复杂性是NP难的。

2 算 法

在本节中，将介绍ST算法。采用DRL算法对链路权值设置和SR配置进行离线优化，采用线性规划方法在线优化流量路径和分流比。

2.1 ST算法框架

首先介绍了ST的框架。这里所考虑的问题不仅是一个TE问题，也是一个网络设计问题。一旦在网络设计阶段确定了SR节点的部署，则长时间内不能改变。OSPF重配置可能会引起诸如micro-loop等问题[13]，因此OSPF链路权重在网络运行阶段不能快速变化，以保证转发的一致性。更新SR规则不会产生这样的问题，因此SR控制的流量路径可以更容易地改变。

综上可知，ST有两个阶段：

(1)离线网络设计：离线网络设计阶段的目的是获得合适的链路权重和长时间的SR节点部署。考虑到网络流量的周期性，利用历史流量矩阵计算了一个具有代表性的TM。然后使用离线DRL算法的深度确定策略梯度(DDPG)来优化链路权重和SR部署。一旦获得最佳链路权重设置和SR节点部署，它们在网络运行时不会发生变化；

(2)在线路由优化：在这个阶段，确定了链路权重和SR节点部署，并且只针对每个新的TM在线优化路由路径。使用线性规划来决定适当的SR节点分割比率，以最小化每个TM的最大链路利用率。

2.2 离线阶段设计

由于前文描述的优化问题不能在多项式时间内求解，因此采用强化学习。强化学习是机器学习的一个分支。RL不再依赖于人工设计的启发式算法或从预先收集的训练数据(如监督学习)中学习，而是直接与网络交互并从中学习。在RL中，有一个代理通过状态(观察)，行为和奖励与环境反复交互[40]。在每个步骤t中，代理从环境中观察一个状态st并选择一个操作at。根据at，状态转移为st+1，环境向代理发送奖励rt。代理的行为基于一个确定性策略π，它从一个状态映射到一个特定的操作。RL的目标是从起始状态J=其中γ∈(0,1]称为折扣因子)开始，学习使期望累积折扣报酬最大化的最优策略。直观地说，网络就是环境，提出的算法就是代理。将问题转化为RL公式，如下所示：

动作：这里的动作是链接权重设置。更具体地说，作用是一个1×|E|向量，at=[w(e)|e∈E]。

回报：回报rt按式(13)、式(14)计算。使用Umax(st)来表示当网络流量分布为st时最小的最大链路利用率。首先利用式(13)计算Umax(s1)与Umax(st)的比率

(13)

比率α反映了最大链路利用率Umax的改善程度。然后根据式(14)计算回报

(14)

回报告诉代理它的行为有多好，所以基本思想是当α<1时给予负回报，当α>1时给予正回报。使用指数函数的目的是在代理表现良好时给予很大的回报，反之亦然。

算法1：ST 离线阶段

输出：w,SRN,Umax

用随机θμ,θQ初始化Actor网络μ(s|θμ)和Critic网络Q(s,a|θQ)

用θμ′←θμ,θQ′←θQ初始化目标网络μ′(s|θμ′)，Q′(s,a|θQ′)

初始化重播缓冲区R

form=1,2,…Mdo

fort=1,2,…Tdo

rt=get_reward(Umax(s1),Umax(st+1))

R.store(st,at,rt,st+1)

minibatchR′=R.sample(N′)

fortransition(si,ai,ri,si+1)∈R′do

yi=ri+γQ′(si+1,μ′(si+1|θμ′)|θQ′)

endfor

通过最小化损失更新Critic网络

按采样策略梯度更新Actor网络

θQ′←τθQ+(1-τ)θQ′

θμ′←τθμ+(1-τ)θμ′

ifUmax(st+1)=MCFOPTthen

break

endif

endfor

endfor

w,SRN,Umax=aT,SRNT+1,Umax(sT+1)

returnw,SRN,Umax

下面将具体说明：①如何获得所有TMs的代表性TM(get_representative_TM函数)；②如何获得状态st+1，即当链路权重设置为at时，网络流量分布Umax(st+1)和SRNt+1(get_state函数)。

(1)代表性TM：希望找到最佳和最合适的OSPF链路权重设置和SR节点部署，以在相对较长的时间内最大限度地降低SR-TE的链路利用率。因此，不使用任意TM，而是使用过去一段时间内的历史TMs来计算具有代表性的TM。

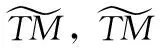
(15)

(2)获取表示网络的状态：在步骤t中，链路权重设置固定为at，需要得到状态为st+1的网络流量分布。与以往文献[15]和文献[16]的网络场景简单不同，本文主要研究分散部署的IP/SRv6网络。为了得到st+1的状态，需要确定SR节点集SRNt+1和转发路径。此外，还需要得到最小的最大链路利用率Umax(st+1)用来计算rt。这里解决这个问题共有3步：选择SR节点；计算流量路径；求解LP问题。

(1)选择SR节点：为了获得SR节点的最优部署位置，充分利用部分部署SR网络所提供的TE能力，需要考虑3个拓扑参数：

1)度：节点的度数(DEG)是指与该节点相关的链接数，可以通过式(16)计算得到

DEG(v)=|{e|es(e)=v∨et(e)=v}|

(16)

在这里，es(e)和et(e)分别代表链路e的头和尾。

2)中间性：节点的中间性是指通过该节点的最短路径数。σst(v)表示从s到t通过v的最短路径数，用当前链路权重计算at

(17)

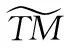
(18)

根据这3个参数分别选择SR节点。对于每个参数，都希望值越大的节点成为SRN中支持SR的节点。所以将对不同的SR配置比进行实验。

(2)计算流量路径：在确定了SR节点的链路权重和位置之后，计算出可用于每个流l的完整路径集。如前所述，每个完整的流量路径可被视为由3种类型的子路径组成。网络设备每个路径只支持有限数量的SID，大的SLD也会增加包开销，因此每个路径使用的节点段(中间点)的数量应该受到限制。在这里设置一条路径最多可以使用K个段，即第二类子路径，然后用一个普通的DFS(深度优先搜索)得到每个流l的子路径。请注意，在DFS时消除了重复的路径和循环。

如图2所示，从节点A到节点H有8个节点，并且显示了它们之间的链接。每条边上的数字表示该链路的权重，SR节点集SRN为 {B,D,G}。从节点A到节点H有一个业务需求。

图2 流量路径计算示例

首先，计算所有可用于流量需求的子路径。表1展示了部分结果：从A到H的最短路径是A-B-C-D-E-H，并且在这条路径上支持SR的节点为B和 D，所以第一类的子路径是A与B,D之间的最短路径，同理，第二类的子路径是节点B、D或G之间的最短路径。第三类的子路径是从节点A到H或从SR节点到H的最短路径。

表1 部分子路径

然后计算子路径形成的路径，每个路径最多只能使用两个节点段，并需要去掉一些重复的子路径，结果见表2。图2中还展示了4条路径P1-P4。以P2为例。数据包遵循从节点A到节点H的最短路径，直到到达节点B。从这里开始，它由SR路由，段列表为[G，D]。数据包依次经过子路径(B，G)和(G，D)，到达节点D，然后通过OSPF协议路由到达目的节点H。在这里，路径(A，B)(B，D)(D，G)(G，H)被消除，因为它与P3重复。

表2 所有有效子路径

再使用Floyd-Warshall算法来计算所有的子路径。然后遍历每个SR节点，得到每个流的第一类和第三类子路径。最后通过所有的SR节点对得到所有的分段。因此，计算所有子路径的时间复杂度为O(|V|3+|L|·|SRN|+|SRN|2)。具有|V|节点和|E|边的图中DFS的时间复杂性为O(|V|+|E|)[44]。用于搜索流量路径的图有|SRN|+2个节点(所有SR节点加上s(l)和t(l))和|SRN|·|SRN|+2)边(考虑任意两个SR节点之间的子路径，s(l)和SR节点，以及SR节点和t(l))。DFS是为每个|L|需求运行的。因此DFS的时间复杂度是O(|L|·[|SRN|+2+|SRN|·(|SRN|+2)])=O(|L|·|SRN|2))。

(3)解决LP问题：在获得所有可用路径之后，需要尝试获得状态st+1，即流量分布，以及用于计算回报的Umax(st+1)。如何最大限度地减少网络中链路的利用率。SR的一个特性是可以为同一个业务流定义多个SL，并且源节点将根据可配置的分割比率在可用SLs上分割业务。用线性规划(LP)来寻找最佳分裂比和对应的st+1和Umax(st+1)。式(19)～式(22)为LP的计算公式

minUmax

(19)

(20)

(21)

0≤fl(p)≤1∀l∈L,p∈Pl

(22)

在这里，Pl表示流量需求l的所有可用路径的集合，p是其中的路径。Sp是路径p使用的子路径集，s是Sp中的子路径。Is,e是表示链路e是否属于子路径s的二进制表达。fl(P)表示路径p上需求l的分流比。式(19)是目标函数。式(20)约束每个流量需求i在其路径上完全路由。式(21)链路所承载的业务量不能超过其容量的限制。式(22)是非负约束。在变量和约束条件相对较少的情况下，该LP问题可以快速求解。这样就可以得到Umax并用fl(P)计算st+1，如式(23)所示

(23)

2.3 在线路由优化

在这个阶段，离线阶段的输出w和SRN作为链路权重的设置和SR节点的部署。而只为每个新TM在线优化路由路径。当w和SRN固定时，所有可用的业务路径也都是固定的。因此，只需要为每个需求确定最佳的分割比率。并且只需针对每个新TM解决LP问题，并获得分流比和Umax。

3 实验与评估

为了更好评估ST算法在部分部署的SR网络中的性能，在此进行实验。

3.1 实验设置与数据集

3.1.1 设置

算法实现是基于Python 3.0和Keras实现的，整个实验是在一台Ubuntu系统的台式电脑上进行，CPU 为英特尔I7 36 Ghz，内存为16 GB。显卡为英伟达RTX 3080。DDPG训练集个数为100，每集500步，前80%使用OU过程噪声。重播缓冲区N设置为3200。minibatchN’为128。折现因子γ为0.9。τ设为0.001。

3.1.2 数据集

(1)拓扑结构：在评估中，对3种小型网络拓扑进行了实验：美国研究与教育网络(Abilene)、中国教育研究网络(CERNET)和欧洲研究与教育网络(GEANT)。此外，还使用了文献[17]提供的3种更大的拓扑：rf3967、rf1755和rf1221。

(2)流量矩阵：Abilene的TMs由TOTEM提供[18]。文献[19]验证了CERNET的TMs。GEANT的TMs数据集由Uhling提供[20]。Abilene和CERNET的TMs每5 min测量一次，所以一天有288次TMs。对于GEANT的TMs每15 min测量一次，所以一天有96次TMs。文献[17]提供了3种较大拓扑的TMs，每个拓扑只有一个TM。对于Abilene、CERNET和GEANT，使用相同的初始链路权重设置和链路容量，并使用拓扑数据提供的链路权值设置和链路容量，用于3种较大的拓扑。

3.2 实验结果评估

3.2.1 离线网络设计性能

(1)SR节点选择方法：首先尝试确定最佳SR节点选择方法。

结果如图3所示，其中SRD-1和SRD-2是具有一个或两个SRD的SRD方法，如文献[1]所述，其它3条曲线对应于的ST算法，它有3种SR节点选择方法DEG、BTW和MLL。将每个路径K使用的最大节点段数设为1，并在不同的SR节点部署率下进行了实验。在图3(a)和图3(b)中，当SR_Ratio=0.1时，没有显示ST和SRD-2 的Umax，因为网络中只有一个SR节点。但是SRD-1方法仍然可以处理邻接段，因为它可以指导流通过SR节点的特定接口。SRD-1和SRD-2的Umax在图3(d)和图3(e)中没有显示，因为文献[1]提出的混合整数线性规划(MILP)无法在300小时内求解。

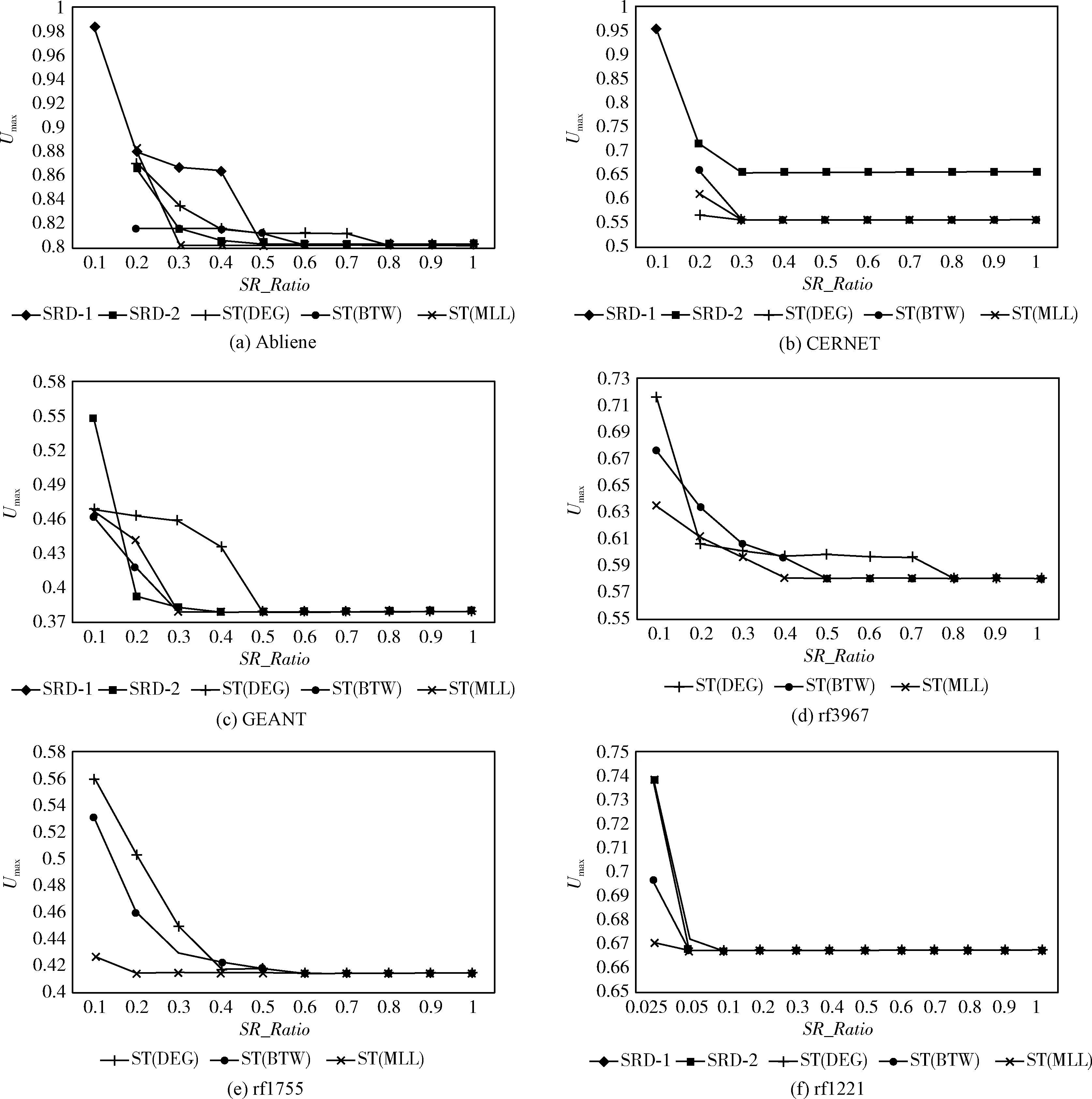
图3 最大链路利用率与SR部署比率之间的关系

根据实验结果可知，最佳的SR节点选择方法是MLL。这是因为MLL与网络中的业务流有关，而DEG和BTW只描述拓扑特性。当SR_Ratio=0.1或0.2时，ST(MLL)的Umax不是最低的。然而，通过MLL选择可以通过较低的部署率实现几乎与全SR网络中相同的TE性能。在Abilene中，当根据MLL选择SR节点时，只有30%的具有SR特性的节点可以获得与全SR网络相同的性能，而按BTW或DEG进行选择时，部署率应为0.6或0.8。GEANT、rf3967、rf1755和rf1221也有类似的结论。在CERNET中，3种SR节点选择方法的Umax差距很小。

图4显示了SRD-1、SRD-2和ST(MLL)在GEANT上，SR_Ratio=0.3，K=1时的SR部署。图中的每条边代表两个方向上的单向链接。很明显，节点0和14是关键节点，因为这3种算法都选择了它们。一个有趣的事实是SRD-1和SRD-2选择相同的SR节点，即0、10、11、12、14和16。虽然SRD-2的输出显示10、14、16是一个SRD，0、11、12是另一个SRD，但是所有SR节点形成一个连通子图。ST(MLL)选择MLL最大的SR节点，不考虑连通性，选择节点0、2、3、4、14、18，尽管2、3、4、14仍然是连通的。ST(MLL)放宽了SRD限制，可以提供更大的路由灵活性。

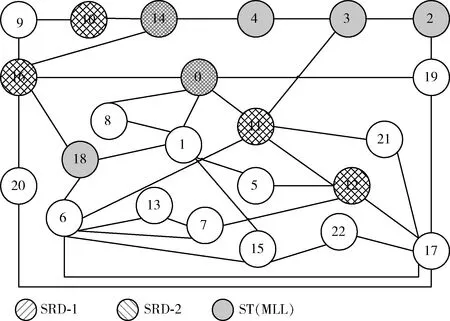
图4 GEANT的SR部署(SR_Ratio=0.3)

(2)SR节点部署率：结果如图3所示。首先可以看出，更多支持SR的节点可以提高TE性能。很明显，Umax随着SR_Ratio=0.1的增加而减小。网络中更多的SR节点将提供更好的TE能力，因为业务流的路由将更加灵活。当网络中SR节点较多时，该算法有机会让网络中的业务进行更好地绕行，从而避免拥塞链路。然而，随着部署比例的增加，改进变得微不足道。

此外，可以看出，在除rf1221外的所有拓扑中，使用ST(MLL)升级20%到40%具有SR能力的节点将获得与全SR网络相同的TE性能。在rf1221中，使用这5种方法中的任何一种，仅升级10%的节点就足够了，而且即使使用ST(MLL)时SR_Ratio=0.25，Umax仍然很低。综合考虑TE性能和计算成本，认为0.3、0.3、0.3、0.4、0.2和0.05分别是ST(MLL)最合适的SR_Ratio。如果采用其它方法进行选择，则配置比例应更高，以获得相同的结果。然而，如果使用SRD-1ss或SRD-2方法，则需要分别对Abilene、CERNET和GEANT中的50%、30%、40%的节点进行SR特性升级，以获得与所有具有SR特性的节点升级所获得的Umax相当的值。在CERNET中，即使SR_Ratio=1.0，ST和SRD的Umax之间也存在明显的差距。这是因为本文的算法在多个路径上路由一个需求，而SRD只对一个需求使用一个单独的路径。

(3)每个路径K可以使用的节点段数：以前的实验是在K=1的情况下进行的。现在分析不同K值对结果的影响。结果见表5，将6种拓扑的SR_Ratio分别设置为0.3、0.3、0.3、0.4、0.2和0.05，并根据MLL选择SR节点。然后在K=1和2时用3种拓扑进行了实验。为了进一步验证ST的TE能力，还给出了用Gurobi求解MCF问题的最优解。

很明显，K值越大，链路利用率越高。但Umax在所有拓扑中没有差异，即使结果精确到小数点后5位。MCF问题假设任何网络节点都可以以任意比例对流进行分馏，这在现实中是不可行的。仍然接近最优解。但是，K越大，计算时间就越长。这是因为K值越大，LP问题中的可用路径和变量越多，从而增加了求解问题的时间。因此，最多使用一条路径K=1提供足够的能力。

3.2.2 重量调整的必要性

算法的一个关键思想是权值调整(WA)。现在用实验来强调它的必要性，结果如图5所示。将结果与WA(用ST(MLL)表示)和没有WA的结果进行了比较，这意味着采用初始权重设置而不改变它(SRTE(MLL，K=1)和SRTE(MLL，K=2)。此外，还展示了一个经典的OSPF网络TE工作的结果，只优化了OSPF权重[21](用OSPF权重优化表示)。为了进一步展示WA方法的性能，在这里展示了使用文献[21]中的局部搜索(LS)作为权重调整方法，并且仍然使用SRTE来获得每个搜索节点的Umax(LS-SRTE(MLL))的结果。

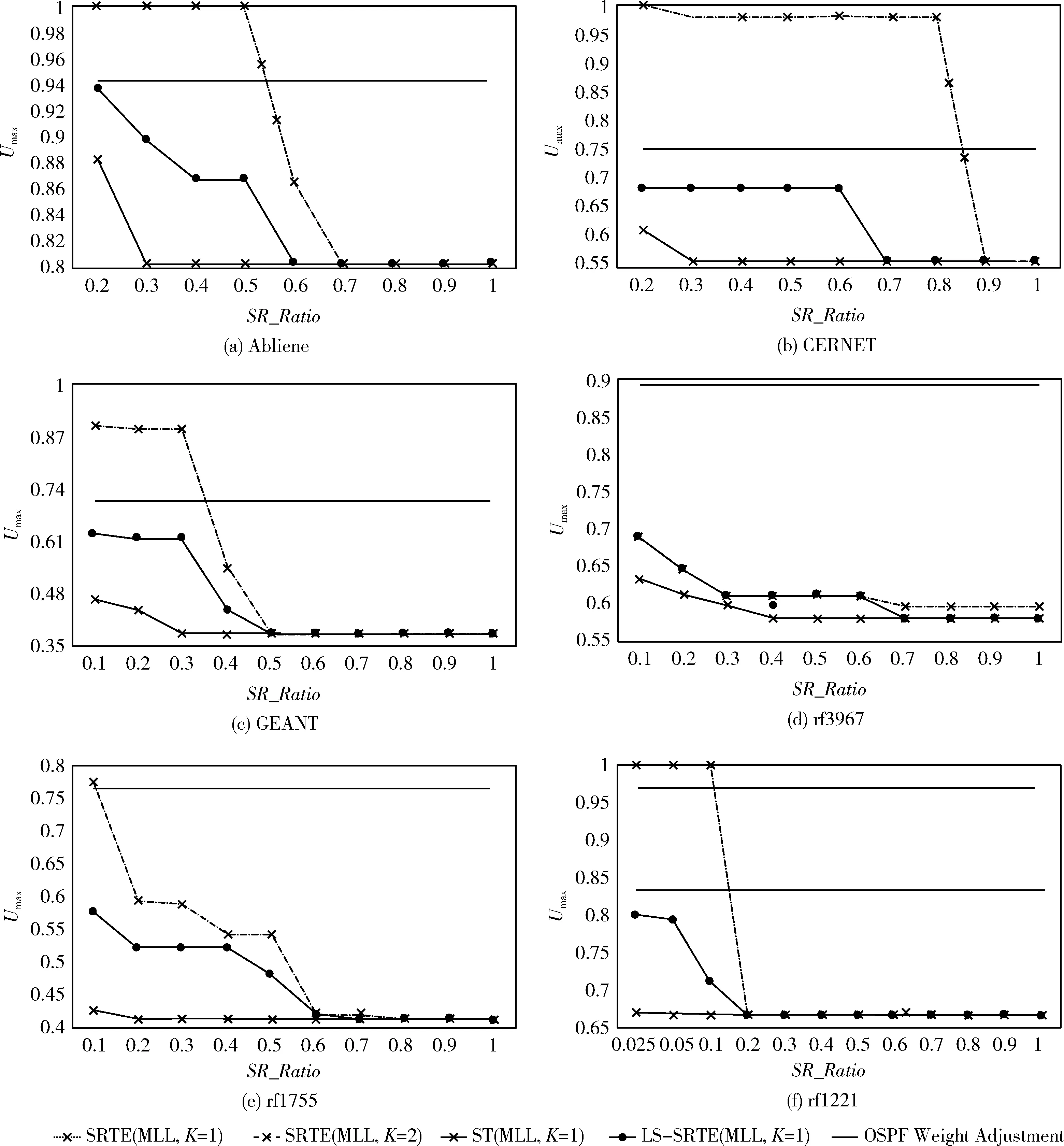
图5 最大链路利用率与WA之间的关系

首先，认为WA是必要的和关键的，它比使用大K值更有效。ST(MLL，K=1)获得的Umax显著优于SRTE(MLL，K=1)的结果。当使用SRTE(MLL，K=1)时，超过一半的节点需要使用SR特性进行升级，以在大多数拓扑中获得较低的Umax。特别是当SR_Ratio≤0.3时，大多数拓扑结构的WA-ST(MLL，K=1)与SRTE(MLL，K=1)的Umax有很大的差距。然而，SRTE(MLL，K=1)和SRTE(MLL，K=2)的Umax非常接近，甚至在大多数情况下是相同的，因此将K提高到2并不能显著改善结果。继续提高K值可能会得到更好的结果，但请注意，网络设备只支持有限数量的SID。

其次，使用的WA方法比文献[21]中的LS方法更有效。在所有拓扑中，使用ST(MLL，K=1)获得的Umax优于LS-SRTE(MLL，K=1)的结果。SR_Ratio=0.3，K=1，MLL的Abilene训练进度如图6所示。Umax通过训练得到了明显的改善。第10个集之前的Umax有时甚至大于2，但在第80个集之后，即OU过程噪声未被添加时，Umax几乎是稳定的。

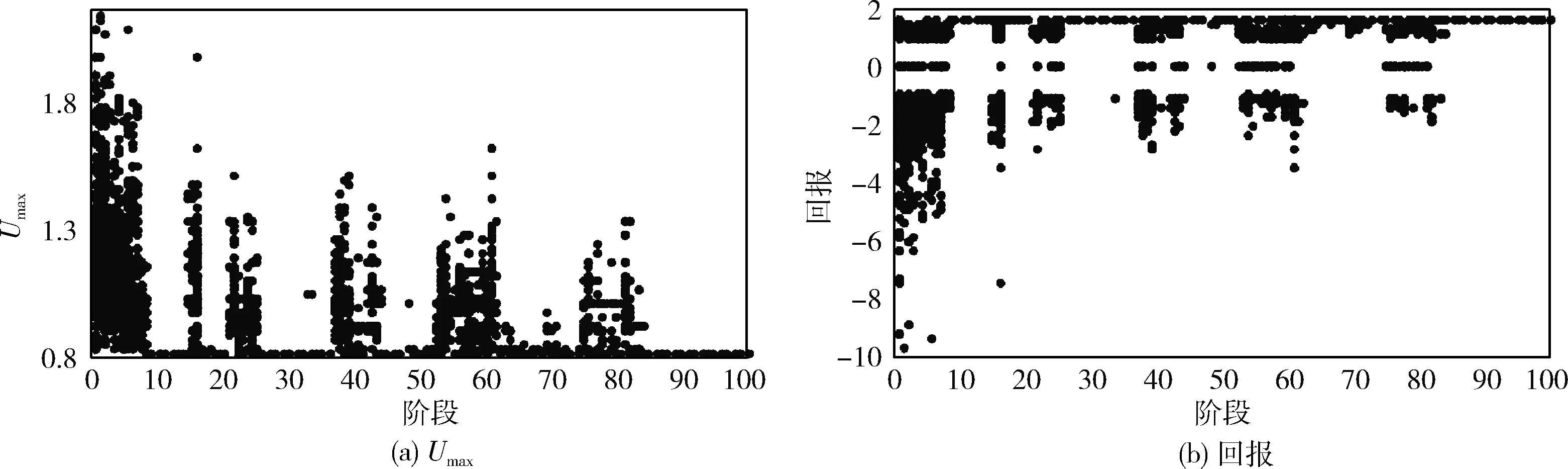
图6 不同学习阶段的Umax和回报

最后，ST(K=1)在SR_Ratio=0.1的情况下，仍优于OSPF权重优化。尽管OSPF权重优化在3种小拓扑中的性能优于拥有较小SR_Ratio的SRTE(K=1)和SRTE(K=2)，但在3种较大的拓扑中，它的性能几乎是最差的，这意味着文献[13]中的局部搜索方法可能不能很好地伸缩。

SRTE的结果比SRD-1和SRD-2差，因为SRD方法不限制每条路径使用的段数。但由于硬件的限制和数据包的开销，必须考虑这种段列表长度的限制。

3.2.3 流量变化时的在线性能

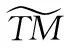
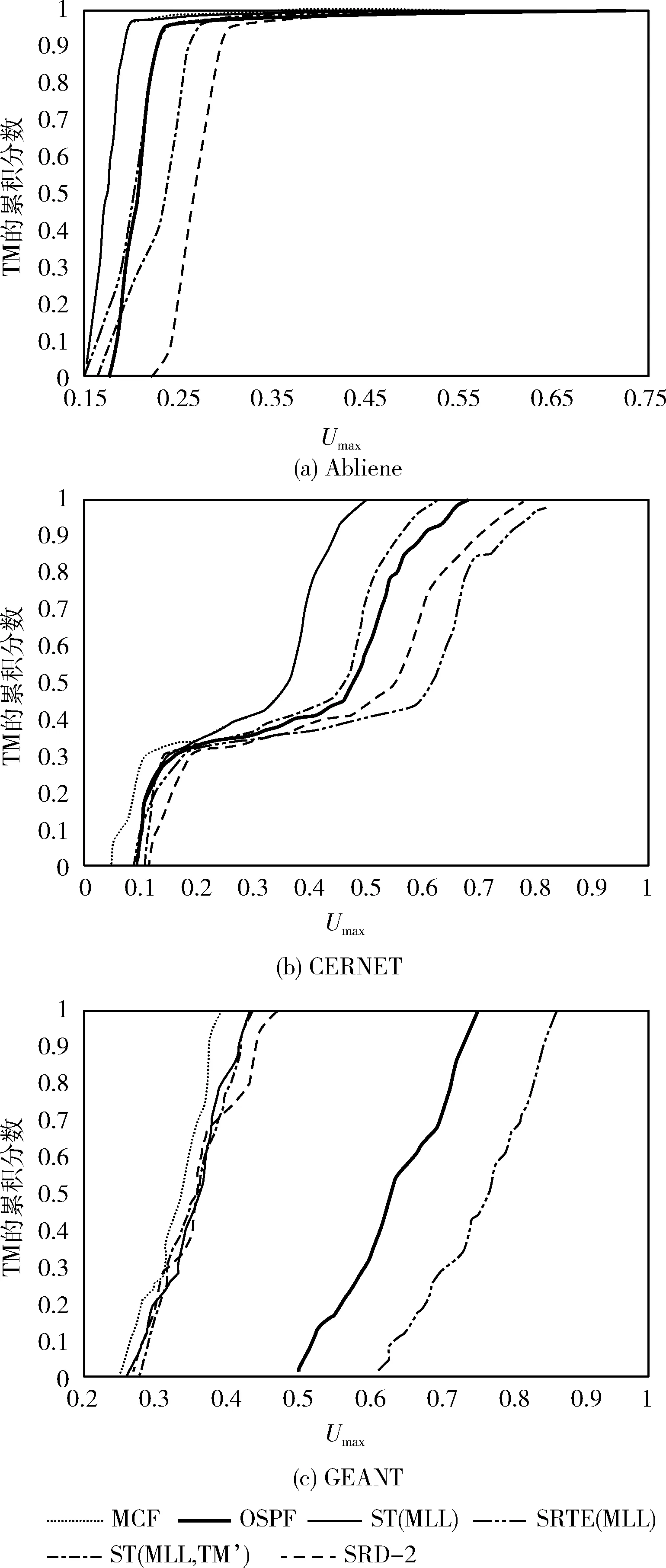
图7 使用不同算法的所有TM的最大链路利用率

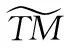
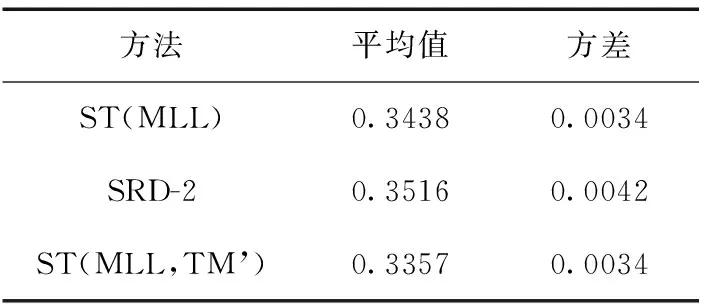
表3 GEANT中的Umax的平均值和方差

4 结束语

本文研究了部分部署的SRv6网络中，SRv6节点分散部署时的TE问题。该算法结合了OSPF网络和全SR网络的TE思想。采用强化学习算法DDPG对链路权值和SR节点配置进行优化，并通过求解一个线性规划来确定最佳业务分流比。实验和评估结果表明，该算法在实验拓扑和TMs上表现良好。ST算法可以实现几乎与部署了20%～40%的SR节点的完整SR网络中相同的TE性能。此外，进一步的实验验证了在混合IP/SR网络中进行权值调整的必要性。提出的方法在流量变化时表现良好。在未来，将进一步研究更大规模的混合IP/SR网络的在线TE算法，包括流量变化、公平性考虑和故障恢复。