基于特征聚类集成技术的在线特征选择
杜政霖,李 云
(1.南京邮电大学 计算机学院,南京 210003; 2.桂林电子科技大学 广西高校云计算与复杂系统重点实验室,广西 桂林 541004) (*通信作者电子邮箱simondzl@163.com)
基于特征聚类集成技术的在线特征选择
杜政霖1*,李 云1,2
(1.南京邮电大学 计算机学院,南京 210003; 2.桂林电子科技大学 广西高校云计算与复杂系统重点实验室,广西 桂林 541004) (*通信作者电子邮箱simondzl@163.com)
针对既有历史数据又有流特征的全新应用场景,提出了一种基于组特征选择和流特征的在线特征选择算法。在对历史数据的组特征选择阶段,为了弥补单一聚类算法的不足,引入聚类集成的思想。先利用k-means方法通过多次聚类得到一个聚类集体,在集成阶段再利用层次聚类算法对聚类集体进行集成得到最终的结果。在对流特征数据的在线特征选择阶段,对组构造产生的特征组通过探讨特征间的相关性来更新特征组,最终通过组变换获得特征子集。实验结果表明,所提算法能有效应对全新场景下的在线特征选择问题,并且有很好的分类性能。
组特征选择;聚类集成;流特征;在线特征选择
0 引言
特征选择是机器学习和数据挖掘中的关键问题之一。特征选择是通过去除数据集中不相关的和冗余的信息来获得最优特征子集的过程[1],因此,特征选择是维数约简的一个重要且常用的方法。特征选择主要有三个方面的作用:提高算法对后续未知样本的预测性能;通过选择与任务相关的特征来解释问题和降低特征空间维度。特征选择可应用于诸多领域,尤其是对涉及高维数据的问题[2-3]。
虽然对于特征选择已经有了深入的研究,但是目前对于特征选择的研究大多受限于批量学习。在批量学习中,特征选择以离线的形式进行,并且训练样本的所有特征都是提前给定的,因此,对于不知道训练数据的全部特征空间或者获取全部特征空间的代价太大的情况下,批量学习的方法并不适用[4]。为此,近年来又提出了在线特征选择。在线特征选择与传统特征选择最大的区别就是训练数据的特征空间是动态变化的。现有关于在线特征选择的突出工作是Wu等[5]提出的在线流特征选择方法。在线流特征选择所研究的应用场景是特征逐个流入,新流入的特征即刻被在线处理,而不需要等待特征空间的全部信息。换言之,在线流特征选择选择在算法开始时,并没有任何训练数据,随着时间的推移,流特征逐步到达,训练数据才会慢慢积累,并且这个过程可以是无休止的。
然而,现在本文所研究的在线特征选择问题面对的是一个全新的应用场景。在该场景下,训练数据既包括历史数据,又包含流特征数据。因为在现实中的诸多应用领域,对于在线特征选择问题,很多情况下已有了一定的历史数据作为当前训练数据集,同时,训练数据的特征空间又会随着流特征的加入而动态变化,因此,既要充分利用已有历史数据,同时还要对包含流特征的新数据进行在线特征选择。例如,在新浪微博中,热门话题每天都在变化,当一个新的热门话题出现时,它可能包含一些新的关键字(特征),这些关键字可能是新颖的网络词语,也可能是某些词语缩写。虽然已有了大量的历史数据,但是并不包含这些新特征,并且这些特征可能对确定话题来说起着关键作用。再比如,对于垃圾邮件过滤系统,或许已经根据已有历史数据建模,但是垃圾邮件中的广告可能是新产品的广告,这些广告所涉及的特征可能是历史数据中未包含的新特征。此时,如果再建模中没有包含对新特征的处理,那么必将对系统的预测性能产生严重影响。这就要求构建一个有效的学习方法来解决既有历史数据,又有流特征数据的特征选择问题。
为了有效解决上述全新场景下的在线特征选择问题,本文提出了一种基于特征聚类集成技术的在线特征选择算法。该算法充分利用了历史数据和流特征数据,并能有效解决上述全新场景下的在线特征选择问题。此外,本文所提出的算法在保证准确率的同时考虑了算法的稳定性。总体来说,工作主要有以下几个方面:1)为了提高算法对特征选择的稳定性,采用了基于组特征选择的方法;2)将组特征选择和流特征模型相结合,提出了一种新的去冗余策略;3)提出了一种基于特征聚类集成技术的在线特征选择算法来解决全新场景下的特征选择问题。
1 相关工作
动态特征空间下的特征选择问题即为在线特征选择。有关在线特征选择的相关工作早期是在2003年,Perkins等[6]把上述问题归结为在线特征选择问题。在线特征选择与在线学习主要区别在于,在线特征选择可用于动态且未知的特征空间,而在线学习需要在算法开始前知道训练数据的全部特征空间。为此,早期的主要工作有:Perkins等[6]在2003年提出的在线特征选择算法Grafting,Zhou等[7-8]在2005年提出的Alpha-investing算法。Grafting算法将特征选择的预测器融合到正则化框架下。Grafting面向二元分类,目标函数是一个二元负对数释然损失函数。Grafting有如下一些限制:首先,由于在线选择过程中丢弃了某些特征,这将导致算法不能选择出最优结果;其次,对于已选特征再检测将大幅度增加时间消耗;最后,算法中正则化参数值需要全部特征空间信息。对于Alpha-investing方法,总体来说,能有效地通过调整阈值来进行特征选择,也能处理无限特征流问题,但是并没有对已包含的特征再次评价,这将对后续选择产生影响。其后,在线特征选择的相关研究工作主要分为两个方向:在线特征选择和在线流特征选择。本文的相关研究也是针对其中的在线流特征选择问题。两者的主要区别是,在线特征选择的数据是以样本流的形式动态到来,而在线流特征选择是以特征流的形式动态产生。对于在线特征选择中高维数据以样本形式动态产生的情况,Wang等[9]提出的在线特征选择方法仅需固定少量的特征,根据在线梯度下降算法更新分类器,并通过L1范数实现稀疏,采用 L2范数来防止过拟合。其后,Nogueira等[10]为了进一步提高性能,将Wang等[9]的在线特征选择结合online bagging和online boosting提出了在线集成特征选择方法。
对于在线流特征选择,Wu等[5]在2010年提出了在线流特征选择(Online Streaming Feature Selection, OSFS)方法和它的快速版本(Fast-OSFS),来解决动态且未知特征空间下的特征选择问题。为了无需等待训练数据的全部特征空间信息,则需要即刻处理逐个流入的特征,因此,提出了流特征模型,即将动态且未知的特征空间建模为流特征,并根据特征相关性理论,提出了一种用于处理流特征模型的特征选择框架。该框架对于流特征的处理主要分为两个阶段:相关特征的动态鉴别和冗余特征的动态剔除,同时通过所提出的在线流特征选择算法和其加速版本验证了所提出框架的有效性。为了提高算法的准确性和可扩展性来应对更高维数据, Yu等[11]在2014年又提出了SAOLA(towards Scalable and Accurate OnLine Approach)算法,这也是在线特征选择最新并且最有效的方法。在SAOLA算法中,每当流入一个新特征,首先判断该特征是否是相关特征。如果是相关特征,则判断该特征相对于当前最优特征子集是否是冗余特征。如果该特征不是冗余特征,则判断如果将该特征加入到当前最优特征子集中,是否会导致子集中的其他特征会因此变成冗余特征。如果没有的话才会保留该特征。其中冗余分析是通过探讨两两特征间的相关性来实现,这也替代了OSFS和FAST-OSFS算法中的搜索特征子集来去除冗余的过程,从而大幅度提高了时间效率。对于SAOLA算法,存在如下问题:1)SAOLA没有明显地考虑到特征选择算法的稳定性;2)在冗余分析阶段, SAOLA中探讨两两特征之间的冗余性,即1∶1的冗余性,没有考虑1∶m的分析;3)不能有效应用于既有历史数据,又有包含流特征的新数据的场景。为此,本文结合组特征选择和在线流特征选择,提出了一种新的在线特征选择方法。首先通过聚类集成的组特征选择来提高算法的稳定性,并且对于流特征的冗余分析中,采用一对多的去冗余策略,在聚类集成的组特征选择中生成的每个特征组中选择出最终特征的同时去除冗余特征。
2 基于聚类集成的在线特征选择
针对既有历史数据又有流特征数据的全新场景下的在线特征选择问题,提出基于特征聚类集成技术的在线特征选择方法。该方法在对历史数据特征分组中,采用基于聚类集成技术的组特征选择[12-13],并将原算法中的组变换策略加以调整,通过特征与类别的相关性最大的原则来进行组变换,以适应本文场景。所提算法的基本框架如图1所示,主要包括两个部分:1)对历史数据进行基于聚类集成的组特征选择。该阶段主要目的是构造出初始特征组,包括聚类和集成两个关键步骤。2)对流特征数据进行在线特征选择。该阶段主要是对流特征分组,并通过组变换得到最终特征子集。

图1 基于特征聚类集成技术的在线特征选择框架
2.1 组特征选择
由于在高维数据中,通常存在高度相关的特征组,称作固有特征组。每个组内的特征对于类标签具有相同的相关性,并且特征组并不会受训练样本变化的影响[14],因此,可以通过确定特征组的方式来提高特征选择的稳定性。换言之,可以通过寻找一些特征组来近似固有特征组,然后在这些特征组描述的特征空间上执行特征选择。现有的组特征选择的通用算法框架如图2所示。组特征选择包括特征组构造和特征组变换两个关键步骤。
特征组构造主要有两种方法,即数据驱动和知识驱动方法;其中知识驱动方法是根据领域知识来识别特征组,而数据驱动方法产生特征组的过程与领域知识无关,仅考虑数据本身的特性。常用来识别特征组的数据驱动方法有聚类分析[15]和密度估计[16]。虽然许多聚类分析中许多经典的划分方法都能用于产生特征组,例如k均值或层次聚类等;但是,若对特征组的稳定性有一定的要求,那么这些方法都不能很好地适用。数据驱动方法由于充分利用了原始数据的特性,因此得到了广泛的应用,但也正因为这样,数据驱动方法有一个不足之处,便是不能很好地解释所识别出的特征组。本文采用的是数据驱动的方法,主要是基于特征聚类集成技术的组构造方法。
特征组变换是根据组构造阶段产生的特征组集合,在每一个特征组中选择出一个代表特征。从高度相关的特征组中选出一个代表特征,相当于降低特征冗余性。常用的特征组变换方法可以是特征值平均〖17〗等较简单的方法,也可以是组成分析〖18〗等复杂的方法。本文采用的是求特征与类别标签的相关性最大的策略。

图2 组特征选择框架
Fig. 2 Group feature selection framework
2.2 特征聚类集成方法


图3 聚类集成框架
聚类集成算法要解决的问题主要有两个:一是如何产生一个聚类集体,该集体包括多个不同的聚类结果;二是通过何种方法从这多个不同的聚类中得到一个统一的聚类结果,即为集成问题。对于第一个问题,可以采用聚类分析这一无监督特征选择的重要方法,但由于聚类分析的不可能性定理〖19〗,即任何一个聚类算法不可能同时满足尺度不变性、丰富性和一致性。为此,需要根据集成学习〖20〗的思想来解决第二个问题,即通过对多个不同的弱基类模型组合来得到一个性能较好的集成模型,因此本文采用一个新的组构造策略,即聚类集成的方法,由于它在聚类分析的基础上结合了集成策略,因此有更好的平均性能,并且能获得单个聚类算法无法得到的组构造结果〖21〗,其中,聚类集成首先要做的就是产生多个不同的聚类结果,组成一个聚类集体,常用的方法有:
1)数据集相同,采用的聚类算法也相同,但是设置不同的算法参数,来构成多个聚类结果〖22〗。
2)在相同数据集上采用不同的聚类算法,从而得到多个不同的聚类结果〖23〗。
3)首先对原始数据集进行多次抽样得到多个不同的子数据集,然后采用相同的聚类算法在这多个子数据集上进行聚类,从而构成多个聚类结果〖24〗。
4)首先获得原始数据集的多个特征子集,然后在这多个特征子集上采用相同的聚类算法,从而得到多个聚类结果〖25〗。
本文在组构造阶段,使用相同的聚类算法在数据集的不同采样子集上聚类,从而得到多个聚类结果〖26〗。具体实现如下:首先,采用bagging方法[27]的思想来训练基分类器,即通过有放回的抽样来获得不同的样本子集。假设通过bagging方法得到个不同的样本子集,其中单个聚类器采用基于特征相似性的k-means方法,需要注意的是,此处k-means方法与传统k-means不同之处是本文对特征聚类,具体实现如下:
1)初始化k个特征作为聚类中心。
2)分别计算其他所有特征与这k个中心的相关系数,并加入到相关系数最大的簇中。
3)更新中心特征。取簇中与中心特征的相关系数的平均值最接近的特征作为新的聚类中心。
4)将全部特征按照新的中心重新聚类。
5)迭代一定次数或中心不再变化。
其中特征之间的相似性度量策略选用相关系数。两个随机变量u和v之间的相关系数ρ定义如下:
(1)
var()代表变量的方差,cov()代表两个变量的协方差。如果u和v之是完全相关的,也就是存在确切的线性关系,ρ(u,v)是1或-1。如果u和v是完全不相关,ρ(u,v)是0,因此,可用|1-ρ(u,v)|来度量两个变量u和v的相似性。

通过上述基于特征相似性的k-means方法得到多个聚类结果组成的聚类集体后,下面就需要采用合适的集成策略来对聚类结果集成。本文采用的是基于互联矩阵[22]的方法。首先,对m个聚类结果,计算每一对特征被分在同一组中的次数,再除以聚类次数m,由此构成相似度矩阵W。W(q,r)表示特征q和特征r之间的相似度。然后,采用凝聚型层次聚类,对所有特征合并,合并原则是特征组间的相似性大于θ,θ为用户自定义的参数。其中特征组间的相似性采用类平均法计算,以此来降低异常值的影响。例如对于给定的d维数据,通过多次聚类,并得到相似度矩阵W后,具体的集成方法如下:
1)开始时每个特征为单独的一个组,则共有d个组。
2)根据合并原则,如果两组之间的相似性大于给定阈值θ,则两组合并,特征组总数减一。
3)合并后,重新计算新产生的组和其他所有组间的相似性,采用类平均法。
4)重复2)、3)步,直到所有组之间的相似性都小于θ。
通过以上聚类,可以构造出多个特征组 {G1,G2,…,Gs}。至此,基于聚类集成的组特征选择已完成组构造阶段。接下来便是对于包含流特征的数据进行在线流特征选择。
2.3 在线特征选择
对于流特征数据,本文提出了一种新的在线特征选择方法进行处理。该方法基于组特征选择,利用了组构造产生的特征组。下面首先给出流特征的定义:
定义1 流特征。流特征定义为在训练数据的样本空间不变的情况下,数据的特征空间随时间而变化,且特征逐个流入(或连续产生)。
基于流特征的定义,Wu等[5]提出了在线流特征选择的基本框架,对于新流入特征的处理主要分为两个阶段:
1)相关特征动态鉴别。
2)冗余特征动态剔除。
对于在线流特征选择,其目标根据已经流入的特征,能选出一个当前最优特征子集。本文的在线特征选择阶段便是基于在线流特征选择框架,结合聚类集成技术的组特征选择产生的特征组,提出了一种全新的在线流特征选择方法。该方法在冗余去除阶段避免了Yu等[11]提出的SAOLA算法中对于特征冗余分析仅考虑两两特征间一对一的冗余分析,而是采用单个特征相对于特征组的冗余分析。
在所提方法中,假设根据前一阶段的聚类集成方法对历史数据进行处理,并且已经产生了s个特征组{G1,G2,…,Gs},那么,对于在线特征选择阶段流入的特征f,本文要判断流特征f和每个组的相关性,并将流特征f加入到相关性最大的组中。其中流特征f与组之间的相关性通过计算流特征f与该组代表特征的相关性来实现,对于离散值数据,相关性计算方法采用互信息。给定两个变量A和B,则A和B之间的互信息定义如下:
I(A;B)=H(A)-H(A|B)
(2)
其中,变量A的熵定义为:
(3)
对已知变量B时,变量A的条件熵定义为:
(4)
其中:P(ai)是变量A=ai的先验概率,P(ai|bi)是ai在B=bi时的后验概率。
由于互信息用于处理离散值数据,因此对于连续值数据的数据集,本文采用Fisher’sZ-test[23]来计算特征间的相关性。
在上述的流特征的分组过程中,同时还伴随着新建特征组和删除不相关特征组的过程。新建特征组是当流特征与所有特征组的相关性都小于阈值θ2,θ2为用户指定参数,主要是为了避免仅对历史数据进行组构造产生的特征组不全面。而删除不相关特征组是为了避免最终选出的特征子集中包含不相关的特征。通过重复对流特征的分组以及特征组的添加和删除操作,直到没有新特征流入,最终形成了t个特征组{G1,G2,…,Gt}。接下来便是对这t个特征组进行组变换,从每个组中选出一个特征组成最终的最优特征子集。具体的实现步骤如下:
1)流入新特征,计算新特征和每个组的相关性,如果最大相关性大于θ2,则加入到相关性最大的组中;否则,新建组并将其加入;
2)重复步骤1),直到没有新特征流入;
3)删除代表特征与类别相关性小于θ3所在的组;
4)输出每个组的代表特征作为最终特征子集。
本文提出的基于聚类集成的在线特征选择(Online Feature Selection based on feature Clustering Ensemble, CEOFS)算法的伪代码如下:
算法1 基于聚类集成的在线特征选择(CEOFS)算法。
输入:历史数据集D(m个子样本集),流特征数据D′。
输出:特征子集{f1,f2,…,ft}。
3 实验分析
为了验证所提算法的性能,本文将在多个数据集上进行实验,来测试算法的分类性能和时间效率。实验所用到的数据集有:Hill-valley、Urban、Madelon、Isolet、Colon、Arcene。这些数据集均来自UCI数据库[28],其中Urban数据集多分类数据集,其他数据集均为二元分类数据集。各个数据集的详细信息如表1所示。
由于本算法是针对一个从未研究过的全新应用场景下的特征选择问题,因此实验中选取非集成的基于聚类的在线特征选择方法(COFS)和本文提出的基于聚类集成的在线特征(CEOFS)算法做分类准确率的比较实验。实验中所使用的分类器是支持向量机(SVM)和K近邻分类器,SVM中参数C=1,K近邻分类器中K=3(后文直接使用3NN表示)。

表1 实验数据集描述
3.1 分类准确率实验
在这部分实验中,主要研究的是分类准确率的情况。对于本文所提出的CEOFS算法,其中集成次数为10次;同时为了模拟真实场景,假设训练数据的80%作为历史数据,20%作为流特征数据。对于原始数据集Isolet未指定训练和测试样本,使用十次交叉验证,将数据集分成10份,其中9份作为训练数据集,1份作为测试数据集。
通过表2的分类准确率实验结果可以发现,CEOFS算法的准确率相似或高于非集成的在线特征选择算法。对于Arcene数据集上的结果,由于数据维度过高,层次聚类方法并不能完美应对,因此性能受到影响。这也是以后工作要改进的地方。
3.2 运行时间实验
由于现实应用中,对于在线特征选择部分的时间效率有一定的要求,因此本文对CEOFS算法的在线特征选择部分的运行时间做了实验。实验结果如表3所示。
通过以上运行时间的实验可以发现,本文提出的CEOFS算法的时间效率很高。
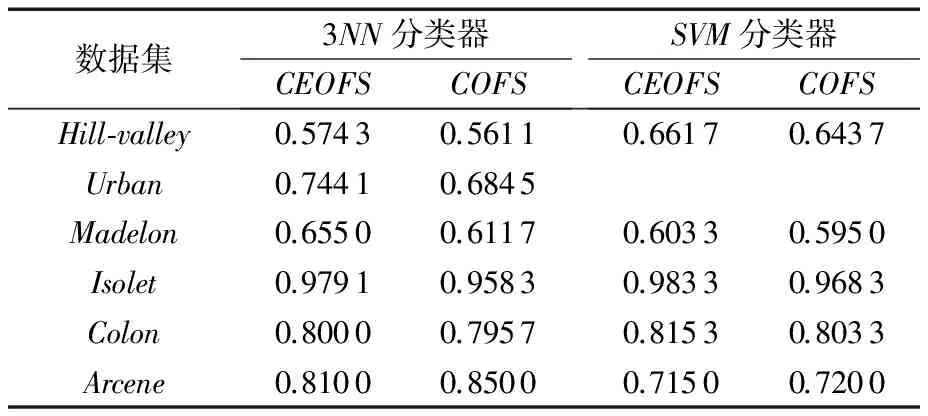
表2 不同分类器的分类准确率实验结果
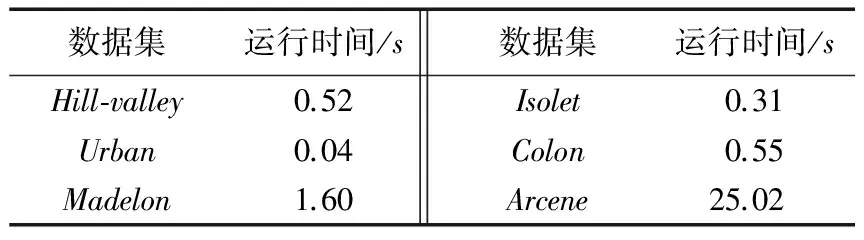
表3 CEOFS算法运行时间实验结果
3.3 相关性阈值实验
对于CEOFS算法,不论是连续值数据还是离散值数据,都需要设定一个相关性阈值θ来判断两个特征是否相关,以此来决定流特征分组情况。本文在数据集Isolet上,设定6个不同的阈值来比较不同阈值对预测性能的影响。
由图4可得,相关性阈值对预测的准确性的影响不大。
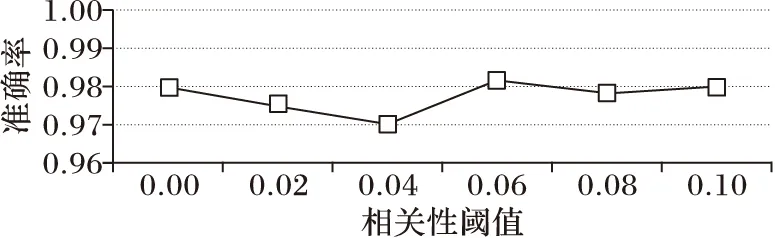
图4 Isolet数据集上相关性阈值对准确率的影响实验
4 结语
本文提出了一个基于聚类集成技术的在线特征选择算法。该算法通过聚类集成的组特征选择来对历史数据进行组构造,并根据特征的相关性来对流特征进行在线特征选择和组变换。实验结果表明所提算法能有效应对既有历史数据又有包含流特征的新数据这个全新场景下的在线特征选择问题。算法在保证分类准确率的同时时间效率也很高,并且该算法考虑了特征选择的稳定性。算法的不足之处在于集成阶段,由于采用层次聚类,因此复杂度较高。这也是在以后工作中需要改进的地方。
References)
[1] 边肇祺,张学工.模式识别[M].2版.北京:清华大学出版社,2000:176-178.(BIAN Z Q, ZHANG X G. Pattern Recognition[M]. 2nd ed. Beijing: Tsinghua University Press, 2000: 176-178.)
[2] DASH M, LIU H. Feature selection for classification [J]. Intelligent Data Analysis, 1997, 1(3): 131-156.
[3] KOHAVI R, JOHN G H. Wrappers for feature subset selection [J]. Artificial Intelligence, 1997, 97(1/2): 273-324.
[4] 李志杰,李元香,王峰,等.面向大数据分析的在线学习算法综述[J].计算机研究与发展,2015,52(8):1707-1721.(LI Z J, LI Y X, WANG F, et al. Online learning algorithms for big data analytics: a survey [J]. Journal of Computer Research and Development, 2015, 52(8): 1707-1721.)
[5] WU X, YU K, DING W, et al. Online feature selection with streaming features [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(5): 1178-1192.
[6] PERKINS S, THEILER J. Online feature selection using grafting [EB/OL]. [2016- 01- 22]. http://public.lanl.gov/jt/Papers/perkins_icml03.pdf.
[7] ZHOU J, FOSTER D, STINE R, et al. Streaming feature selection using alpha-investing [EB/OL]. [2016- 02- 06]. http://www.cis.upenn.edu/~ungar/Datamining/Publications/p384-zhou.pdf.
[8] ZHOU J, FOSTER D P, STINE R A, et al. Streamwise feature selection [J]. Journal of Machine Learning Research, 2006, 7: 1861-1885.
[9] WANG J, ZHAO P, HOI S C H, et al. Online feature selection and its applications [J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(3): 698-710.
[10] NOGUEIRA S, BROWN G. Measuring the stability of feature selection with applications to ensemble methods [EB/OL]. [2016- 02- 03]. http://xueshu.baidu.com/s?wd=paperuri%3A%281a009adab91ad944631001ba336f4e25%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fciteseerx.ist.psu.edu%2Fviewdoc%2Fdownload%3Fdoi%3D10.1.1.728.549%26rep%3Drep1%26type%3Dpdf&ie=utf-8&sc_us=5540872035374925413.
[11] YU K, WU X, DING W, et al. Towards scalable and accurate online feature selection for big data [C]// Proceedings of the 2014 IEEE International Conference on Data Mining. Washington, DC: IEEE Computer Society, 2014: 660- 669.
[12] 黄莎莎.稳定的特征选择算法研究[D].南京:南京邮电大学,2014.(HUANG S S. Stable feature selection algorithm [D]. Nanjing: Nanjing University of Posts and Telecommunications, 2014.)
[13] 黄莎莎.基于特征聚类集成技术的组特征选择方法[J].微型机与应用,2014(11):79-82.(HUANG S S. Group feature selection based on feature clustering ensemble [J]. Microcomputer and its Applications, 2014(11): 79-82.)
[14] LOSCALZO S, YU L, DING C. Consensus group stable feature selection [C]// Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2009:567-576.
[15] AU W H, CHAN K C C, WONG A K C, et al. Attribute clustering for grouping, selection, and classification of gene expression data [J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2005, 2(2): 83-101.
[16] YU L, DING C, LOSCALZO S. Stable feature selection via dense feature groups [C] // Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2008: 803-811.
[17] GUO Z, ZHANG T, LI X, et al. Towards precise classification of cancers based on robust gene functional expression profiles [J]. BMC Bioinformatics, 2005, 6(1): 1-12.
[18] RAPAPORT F, ZINOVYEV A, DUTREIX M, et al. Classification of microarray data using gene networks [J]. BMC Bioinformatics, 2007, 8(1): 1-15.
[19] KLEINBERG J. An impossibility theorem for clustering . 〖2016- 02- 15〗. http://www.cc.gatech.edu/~isbell/classes/reading/papers/kleinberg-nips15.pdf.
[20] DIETTERICH T G. Ensemble methods in machine learning [M] // Multiple Classifier Systems, LNCS 1857. Berlin: Springer, 2000: 1-15.
[21] 罗会兰.聚类集成关键技术研究[D].杭州:浙江大学,2007.(LUO H L. Research on key technologies of clustering ensemble [D]. Hangzhou: Zhejiang University, 2007.)
[22] FRED A. Finding consistent clusters in data partitions [EB/OL]. [2016- 02- 01]. http://xueshu.baidu.com/s?wd=paperuri%3A%284b1317d334fc32b2cec0dde7e8a4ca2b%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fciteseerx.ist.psu.edu%2Fviewdoc%2Fdownload%3Bjsessionid%3D444EE0EED4CB34E00254EB7CB735820B%3Fdoi%3D10.1.1.97.1296%26rep%3Drep1%26type%3Dpdf&ie=utf-8&sc_us=5845832111985885344.
[23] STREHL A, GHOSH J. Cluster ensembles—a knowledge reuse framework for combining multiple partitions [J]. Journal of Machine Learning Research, 2003, 3: 583-617.
[24] FERN X Z, BRODLEY C. Random projection for high-dimensional data clustering: a cluster ensemble approach [C]// Proceedings of the 20th International Conference on Machine Learning. Menlo Park, CA: AAAI Press, 2003: 186-193.
[25] GAO J, FAN W, HAN J. On the power of ensemble: supervised and unsupervised methods reconciled—an overview of ensemble methods [C] // Proceedings of the 2010 SIAM International Conference on Data Mining. Columbus, Ohio: SIAM, 2010: 2-14.
[26] FRED A. Finding consistent clusters in data partitions [M]// Multiple Classifier Systems, LNCS 2096. Berlin: Springer, 2001: 309-318.
[27] PENA J M. Learning Gaussian graphical models of gene networks with false discovery rate control [C]// Proceedings of the 6th European Conference on Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics. Berlin: Springer, 2008: 165-176.
[28] UCI. Machine learning repository [DB/OL]. [2016- 01- 11]. http://archive.ics.uci.edu/ml/.
This work is partially supported by the Natural Science Foundation of Jiangsu Province (BK20131378, BK20140885), the Funds of Guangxi Colleges and Universities Key Laboratory of Cloud Computing and Complex Systems (15206).
DU Zhenglin, born in 1991, M. S. candidate. His research interests include online feature selection.
LI Yun, born in 1974, Ph. D., professor. His research interests include machine learning, pattern recognition.
Online feature selection based on feature clustering ensemble technology
DU Zhenglin1*, LI Yun1,2
(1.CollegeofComputer,NanjingUniversityofPostsandTelecommunications,NanjingJiangsu210003,China; 2.GuangxiCollegesandUniversitiesKeyLaboratoryofCloudComputingandComplexSystems,GuilinUniversityofElectronicTechnology,GuilinGuangxi541004,China)
According to the new application scenario with both historical data and stream features, an online feature selection based on group feature selection algorithm and streaming features was proposed. To compensate for the shortcomings of single clustering algorithm, the idea of clustering ensemble was introduced in the group feature selection of historical data. Firstly, a cluster set was obtained by multiple clustering usingk-means method, and the final result was obtained by integrating hierarchical clustering algorithm in the integration stage. In the online feature selection phase of the stream feature data, the feature group generated by the group structure was updated by exploring the correlation among the features, and finally the feature subset was obtained by group transformation. The experimental results show that the proposed algorithm can effectively deal with the online feature selection problem in the new scenario, and has good classification performance.
group feature selection; clustering ensemble; streaming feature; online feature selection
2016- 08- 17;
2016- 10- 24。
江苏省自然科学基金资助项目(BK20131378, BK20140885);广西高校云计算与复杂系统重点实验室资助项目(15206)。
杜政霖(1991—),男,江苏徐州人,硕士研究生,主要研究方向:在线特征选择; 李云(1974—),男,安徽望江人,教授,博士, CCF会员,主要研究方向:机器学习、模式识别。
1001- 9081(2017)03- 0866- 05
10.11772/j.issn.1001- 9081.2017.03.866
TP391.1
A

