质量检测数据的分析方法研究与实践

李东霖 张向红 郑淑英

考试是对学生学业状态的客观描述，反映了某一阶段学生的学习水平和教师的教学质量情况，具有诊断学情教情、改进加强教学、评价教学质量的功能。在大数据时代背景下，正确应用检测结果，对检查和反思教与学的效果等有一定的参考和指导作用;对学校、班级和任课教师分析前期备考教学成效，发现问题和查找原因等都有重要意义（吴金则，2011）。当前，云南省、昆明市均已建立质量检测网络阅卷平台，虽然为县域提供了区域成绩数据，但所生成的图表针对性不强，如两次考试数据对比没有直观的图表;所提供的指标维度和所形成的报告无法全部满足县域个性化需求等。因此，县域层面普遍还要进行数据的二次分析后才能为开展教学诊断提供支持。昆明市盘龙区立足于自身需求，使用Excel软件自主研发了一套质量分析支架工具，通过多种可视化图表帮助县域提高利用数据开展质量分析的水平。本文旨在通过该支架工具实际应用中的一些具体案例，为县域或教师进行数据分析研究时提供一些方法和思路。

一、数据来源与说明

本文以盘龙区部分学校参加昆明市2021年第二次、第三次高三质量诊断的数据为分析样本，并对具体学校名称以大写字母进行屏蔽。

二、质量分析方法研究

以往的质量分析主要围绕“一分三率”即平均分、优秀率、及格率、低分率展开。这样的分析存在过于关注排名而忽视问题导向的弊端，不利于对教学提供有效指导。基于对昆明市检测平台及反馈数据的梳理，结合盘龙区自身实际，我们针对质量分析方法的问题导向性进行了深入研究。下面介绍四种在盘龙区质量分析支架工具中用到的主要分析方法：

（一）正态分布见趋势

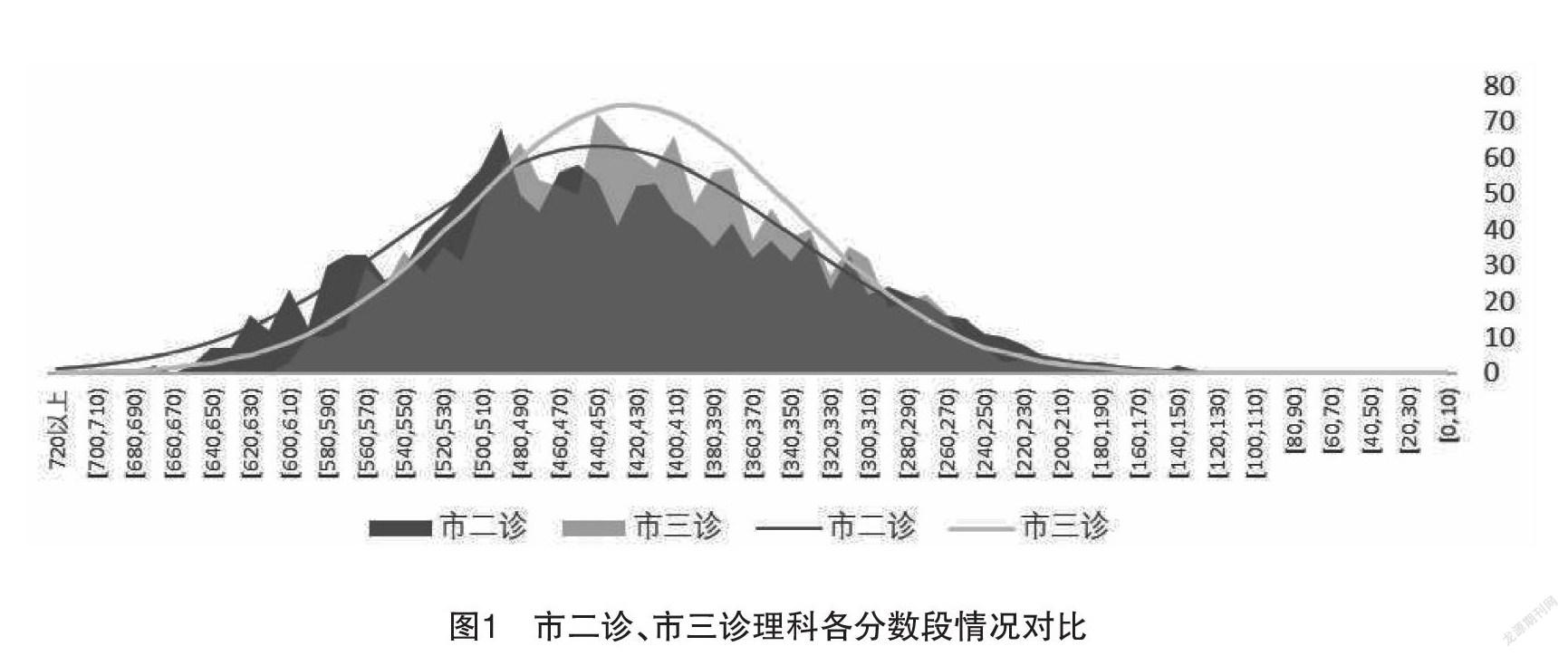
正态分布，也称“常态分布”，又名高斯分布。学生考试分数的分布是有规律的，两头大，中间小，呈现正态分布状态，就是所谓的“钟形”，其“胖瘦”度体现成绩分布的离散程度（张玲，2018）。图1为两次市诊不同分数段学生的分布情况，深色曲线和浅色曲线分别代表了两次市诊的参考曲线（即理想分布）。这两条参考曲线的形态就是“钟形”正态分布的样子。我们通过观察学生实际成绩分布的面积图与参考曲线的贴合度就能得出每次检测成绩的分布是否也符合正态分布。不仅如此，图中深色参考曲线比浅色参考曲线矮“胖”一些，浅色参考曲线比深色参考曲线“瘦”高一些。“胖瘦”的描述形象地体现了数据分布的离散度，离散度在成绩分析中主要指高分段学生与低分段学生的分散程度。离散度越高表示成绩分布越分散，反之表示成绩越集中于平均分附近。例如图1中市三诊的参考曲线“瘦”表示学生成绩相对集中在平均分附近，离散度较低;市二诊的参考曲线“胖”表示学生成绩分散，两极分化情况突出，离散度高，需要适时采取分层施教。

（二）离均差率易对比

由于平均分高低会受试题难易程度的影响，如“平均分82是什么水平”，我们不好回答。为了解决这个问题，需引入离均差率。离均差率，指用比例方式将个体差异定义为个体相对群体平均值的距离，反映了个体在群体中的水平。计算公式：离均差率=（个体均分-总体均分）÷总体均分，当离均差率为正数时表示高于平均水平，当离均差率为负数时表示低于平均水平，当离均差率为0时表示等于平均水平，其数值大小则表示个体在群体中高于或低于平均水平的程度大小。

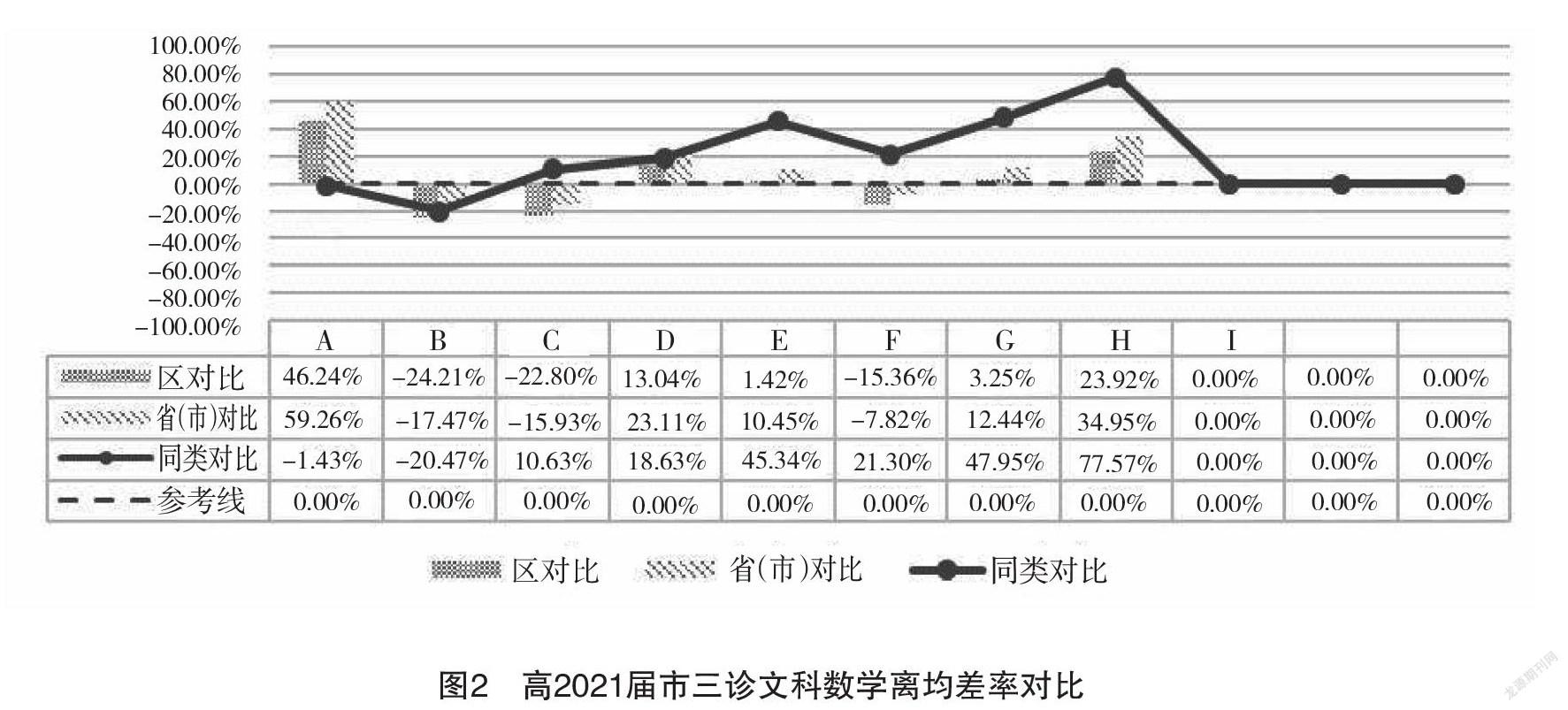
盘龙区数据分析支架工具可以将省（市）、区域、同类校（昆明市将高中依据等级划分为一类、二类和三类校）的离均差率关联在一张由柱状图、折线图共同组成的图表之中（如图2所示）。通过柱状图、折线图与参考虚线（表示离均差率为0）的对比，就很容易直观判断出区域内不同学校数学与省（市）、区域、同类校的水平差异。在图2中，以A校为例，其文科数学水平高于全市和全区，且它在全市的优势大于全区，但在同类校中其又仅仅只是处于平均水平。

（三）“四率”分解见学情

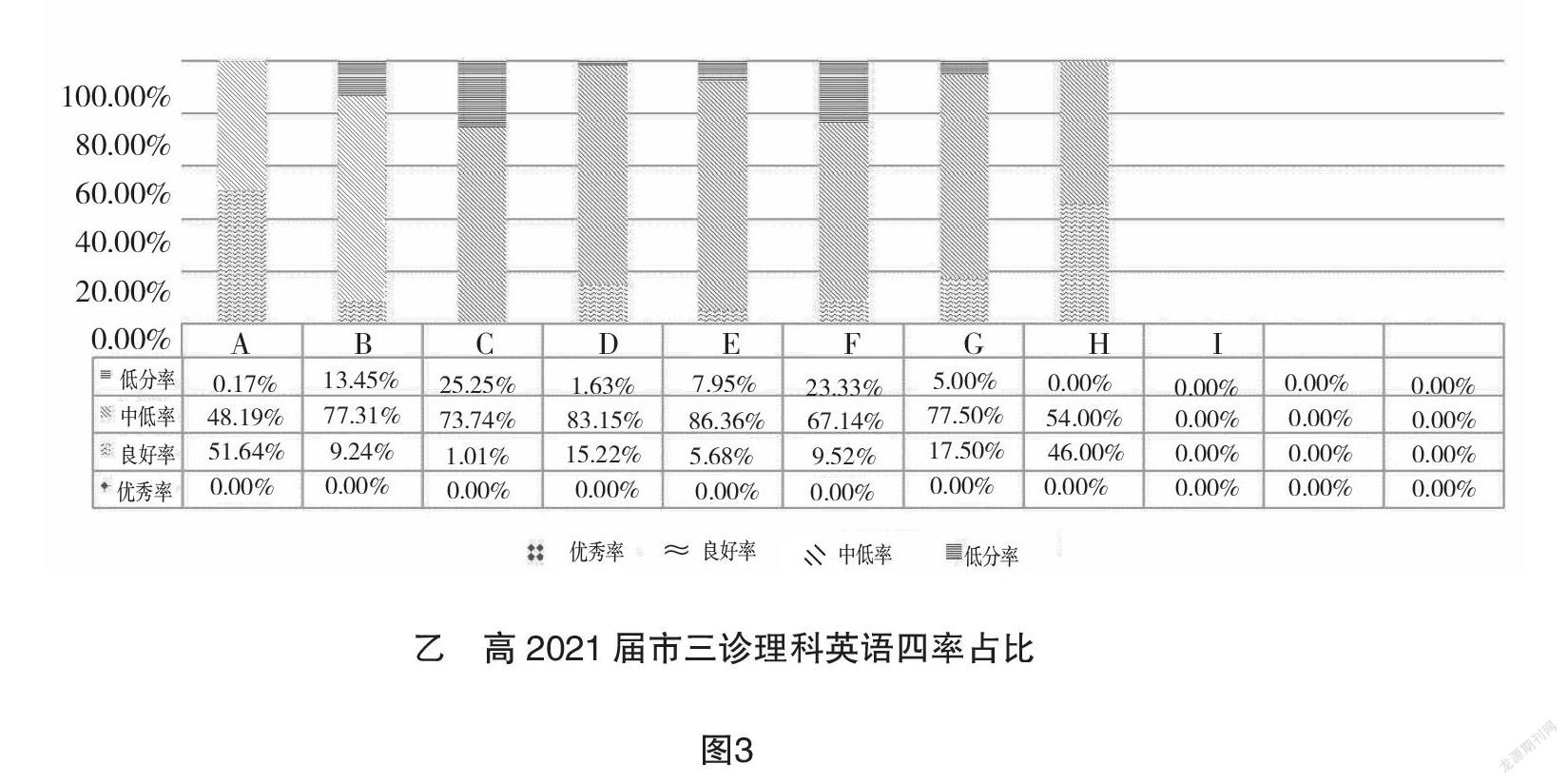
以往质量分析关注“三率”即优秀率（高于满分80%）、及格率（高于满分60%）和低分率（低于满分30%），但“三率”在统计中存在两个主要弊端：一是容易忽略位于满分30%～60%的学生;二是及格率范围和优秀率范围产生了重合。为了获得更加清晰和丰富的层次，我们将“三率”分解为“四率”即优秀率（高于满分80%）、良好率（满分60%～80%）、中低率（满分30%～60%）和低分率（低于满分30%），从而解决了上述弊端。Excel中的堆积柱状图可清晰地呈现各层级学生占比（如图3甲、乙），为精准分层指导提供依据。以理科英语为例，我们可以看出市三诊较二诊优秀率、良好率明显下降，中低率和低分率的占比则明显上升，说明三诊英语试题难度有所加大，对各个层级学生均造成了一定程度的影响。学生对英语试题难度的改变较为敏感，应该在教学过程中适当加强中上难度题型的适应性训练。

（四）数据组合挖新意

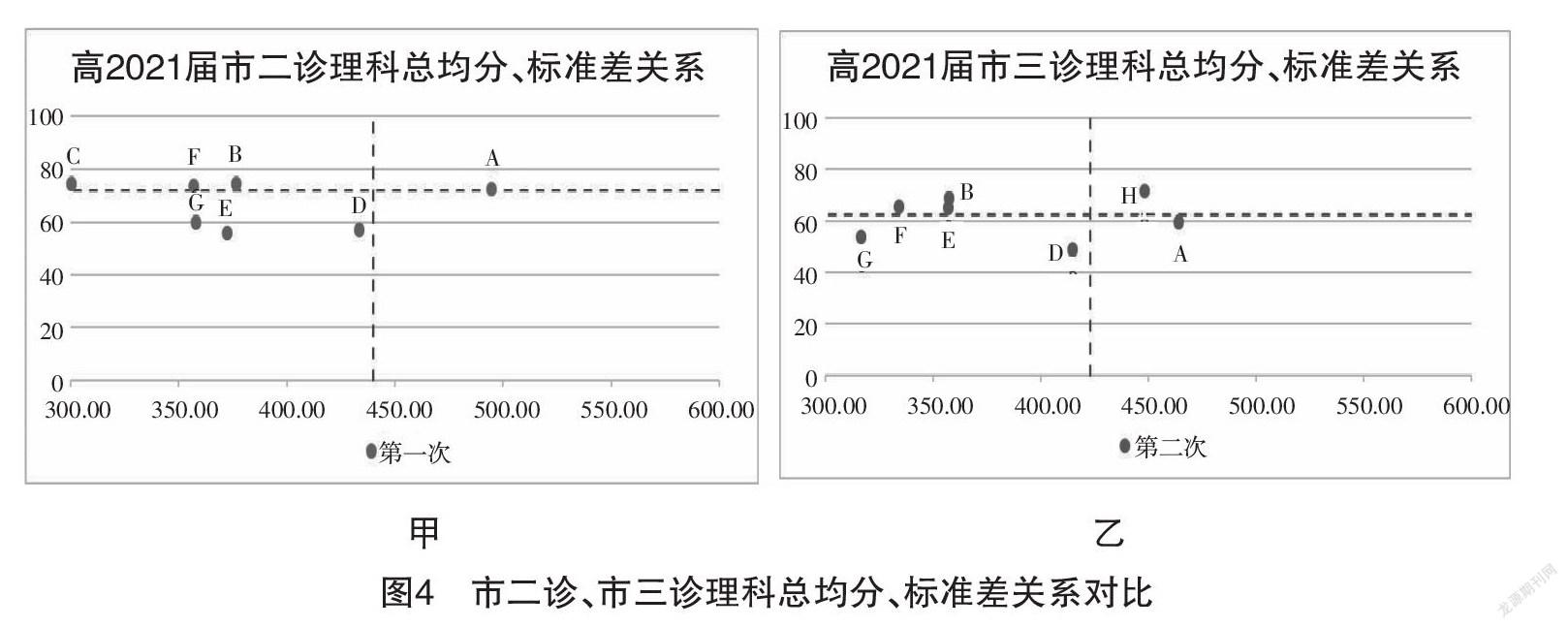
将正态分布中所提到的离散度进行量化，使其与平均分构成一个平面直角坐标系，将会获得更为丰富的信息。离散度量化后被称标准差，标准差也叫方差，是指全体学生成绩之间的离散程度，能更加细致地揭示学生的水平差异。标准差数值越小，说明群体成绩越集中，成绩分布较窄;反之则表示成绩分布较广，两极分化明显。现在，我们把平均分设为x（横）轴，标准差设为y（纵）轴，如图4甲、乙所示，此时区域平均分即图中垂直虚线、区域标准差即图中水平虚线，然后将各校均分与标准差对应x和y值后，方可绘制出相应的坐标点。

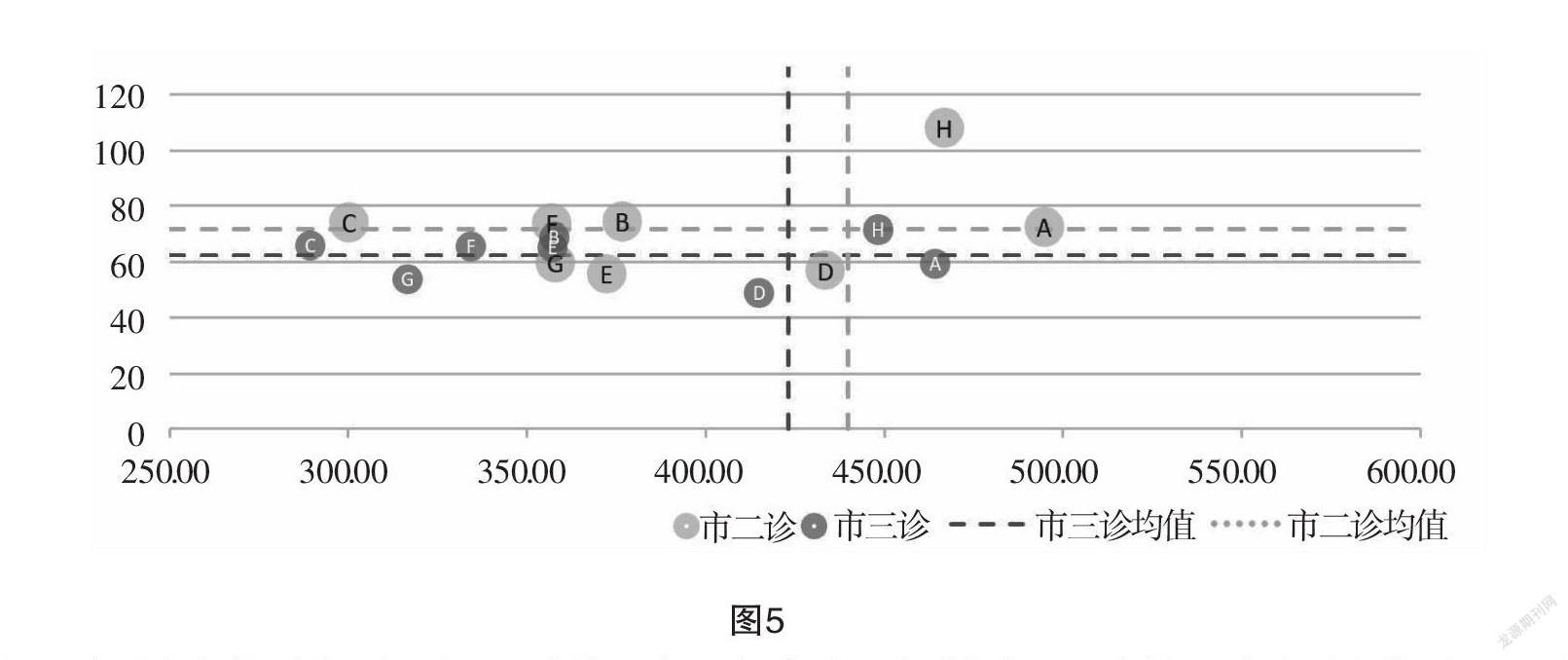
为了便于进一步观察两次诊断的变化，我们将图4甲、乙的直角坐标系进行组合，形成了图5。

在图5中，观察垂直虚线，我们可以发现三诊较二诊左移，表示三诊平均分比二诊低;观察水平虚线，发现三诊较二诊下移，表示三诊标准差比二诊低，反映了二诊时的高分学生群体在三诊时有所萎缩。我们再看各学校情况，以H校为例观察坐标点位置变化，水平方向可以看出其三诊较二诊均分下降了，且幅度超過全区平均降幅（两条垂虚线间距）;垂直方向可以看出学生两极分化虽然得到了一定程度的改善，但分化程度仍高于全区平均（水平虚线）。

三、质量分析支架工具研发思路

（一）数据兼容性好

从任意阅卷系统中获取的学生原始成绩数据，按模板指定格式简单调整后，即可直接复制粘贴到支架工具中形成数据源，随后支架工具便可自动进行分析统计，形成质量分析报告的各项可视化图表。

（二）指标便于调整

质量分析支架工具可根据县域需求自定义相关指标参数，如图6所示，可自定义“优秀率”“良好率”“中低率”“低分率”的上界、下界数值，以及缺考等统计条件，形成个性化分析结果，具有良好的适应性和拓展性。

（三）智能生成报告

质量分析支架工具能够根据数据源和指标参数来智能生成单次考试质量分析报告或两次考试的对比质量分析报告，并能快速输出标准化PDF格式的文件，便于打印和持久化存储。

（四）适应不同场景

为满足现今评价制度改革的需要，一步便可完成县域学校真实名称和替代名称之间的转换，适用于需屏蔽学校真实名称的应用场景（比如区域质量分析会），弱化只关注学校排名不思考存在问题的功利化倾向。

（五）分析准确高效

将多次数据结果进行比对，可确保省（市）、县域、学校、学科四级结果一致，避免因统计算法而导致的数据误差，影响质量分析结果的精准度。将每次区域质量分析报告的制作周期由原来的1～2天缩短到现在的30分钟以内（含初始化数据制作及指标设置等工作），节约了大量的重复工作时间。

教育大数据为教育变革提供了新的思路和技术支撑，在全方位推动着教育变革的同时，也将催生适应时代发展的新型教育治理体系。检测数据作为教育大数据的重要组成部分，为教学活动、教学评价、教育服务、教育决策等提供了数据支撑。盘龙区质量分析支架工具的研制与使用，切实为本区域诊断学情教情、改进加强教学、评价教学质量等提供了高效、全面、可靠的技术支持。

【本文系云南省教育科学规划基础教育专项项目“基于大数据诊断精准改进普通高中教学的策略研究”（项目批准号为BFJC20041）阶段性成果】

◇责任编辑 邱 艳◇