运用思维延续性试题培养学生的问题解决能力——以一道核心素养下的问题解决能力检测题为例

余献虎

(柯城区教学研究室，浙江 衢州 324002)

思维具有延续性，具体表现为从简单到复杂、从基本到综合、从单一到体系，或者由外而内、由此及彼、变化中有不变等.思维延续性试题有利于学生在已有认知的基础上不断深入探析新的数学关系，不断尝试新的思维路径，在挫折和困境中获得真实的解题体验，感悟真实的数学学习，进而提高学生数学学习的习得感，培养并发展学生的数学思维能力和问题解决能力.现以一道核心素养下的问题解决能力检测题为例，与同仁们交流．

1 试题呈现

2)求tan∠BAC的值．

2 试题分析

本题依据圆的基本性质，构造了一个“等角对等弦”的不对称图形.试题表述简洁，结构简单，设问起点低，解答入口宽，重视思维的延续性．试题内容逐步深化，数学思维延续性强，数学关系趋向于本质，有利于学生厘清混沌未觉或杂乱无章的思绪，有利于学生通过训练内化出自我包容、开放的思维习惯，有利于学生问题解决能力的提升．

3 思维延续性的解法探析

学生获得的最直接的问题解决方法取决于他最先关注到的信息，以及由此引起的刺激让他联想到的知识、经验、方法和思想.

3.1 第1)小题解法探析

对于第1)小题，学生最容易关注到的元素是圆周角、角平分线和弧的中点，以及连线后的圆心角、圆内接四边形等，他们普遍会从这些元素入手，探析问题的解决方法．

3．1.1 利用圆心角、圆周角定理及其推论

证法1因为AD平分∠BAE，所以

又因为∠BAE=∠ABC+∠ACB，所以

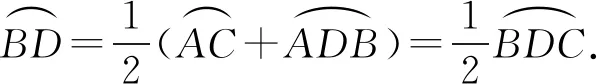
得证.

此法指向清晰，过程简洁、明了，依据是圆周角定理及其推论.若引导到圆心角定理及其推论，则证法如下：

证法2如图2，联结BD，OD，OB，OC，则

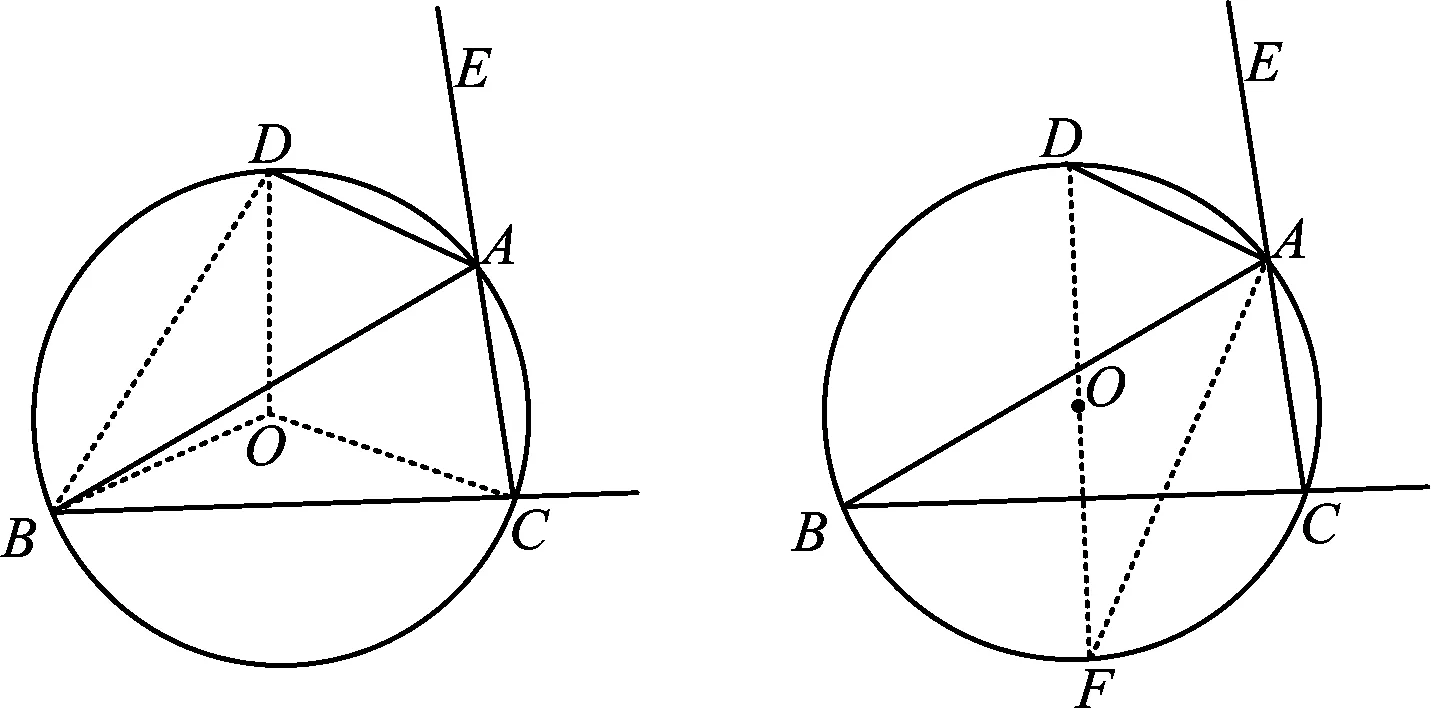
图2 图3

∠BOD=2∠BAD， ∠COD=2∠DBC，

∠DBC=∠DAE.

因为AD平分∠BAE，所以

∠DAE=∠DAB=∠DBC，

从而

∠BOD=∠COD.

得证.

证法3如图3，联结DO并延长交⊙O于点F，联结AF，则∠DAF=90°，即

∠DAB+∠BAF=∠DAE+∠CAF=90°.

又AD平分∠BAE，得

∠DAE=∠DAB，

即

∠BAF=∠CAF，

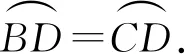
得证.

证法延续学生的知识经验，由等弧想到半圆.类似地，可构造平行线：

证法4如图4，联结CD，作AF∥BC交⊙O于点F，则

图4 图5

∠2=∠B.

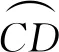
∠D=∠B=∠ACD=∠2，

故

∠4=∠DAB=∠1+∠2=2∠D，

即

∠1=∠D，

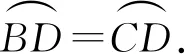
得证．

3.1.2 利用圆内接四边形性质

若看到、读到“∠DAE”联想到的是圆内接四边形，则证法如下：

证法5如图5，联结BD，则

∠DAE=∠DBC.

由AD平分∠BAE，得

∠DAE=∠DAB，

从而

∠DBC=∠DAB，

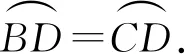
得证.

此法活用圆内接四边形性质，通过等量代换理出解答思路.延续该思路，变化思维路线，可生成如下证法：

证法6如图6，联结BD，CD，则

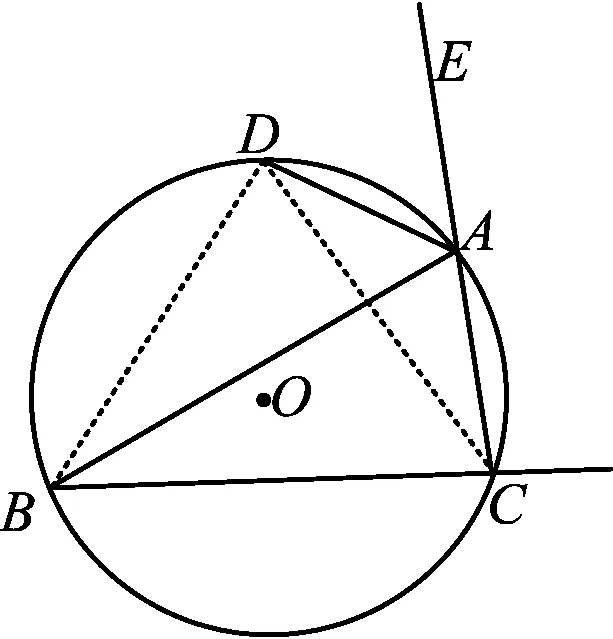
图6

∠DAE=∠DBC， ∠DAB=∠BCD.

由AD平分∠BAE，得

∠DAE=∠DAB，

从而

∠BCD=∠DBC，

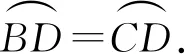
得证.

∠ABD=∠ABC=∠ADC=∠ACD，

所以

∠DAE=∠DBC=2∠ABC.

由AD平分∠BAE，得

∠DAE=∠DAB，

即

∠DBC=∠DAB，

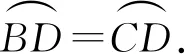
得证.

延续二倍角关系，联系三角形的内角和，用代入消元法可得三倍角：

证法8因为AD平分∠BAE，所以

又因为 ∠DAC=180°-∠DAE

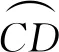
∠DAE=2∠ABC，

所以

2∠ABC+∠DAC=180°，

消元得

∠ACB=3∠ABC，

故

∠DCB=2∠ABC=∠DBC.

得证.

3.1.3 构造全等三角形

延续证法6的对称性和“BD=CD”，可构造全等三角形.

证法9如图7，在AB上截取点F，使得DF=DA，联结DF，DB，DC，则∠DFA=∠DAF.因为AD平分∠BAE，所以

图7

∠DAF=∠DAE，

即

∠DFA=∠DAE，

故

∠DFB=∠DAC.

又因为∠DBF=∠DCA，所以

△DBF≌△DCA(AAS)，

从而

BD=CD.

得证.

综上可知，第1)小题起点虽低，但方法多样，从弧到角、角到线，从直径到互余、和差到倍数，无一不具备解决问题的基本思想方法，需要学生充分理清知识间本质的数学联系，发现转化的路径和变化中的不变性，做到深度思考．

3.2 第2)小题解法探析

第1)小题重在探析由学生“关注到的信息”联想到的问题解决方法，第2)小题重在探析延续第1)小题的思维路径从而生成解决方法，如延续“图7”，就不弃“全等”．

3．2.1 构造全等三角形

解法1如图8，在AB上取点F，使得BF=AD=5，过点D，C作DG⊥AB于点G，CH⊥AB于点H，则△BFD≌△CAD，从而

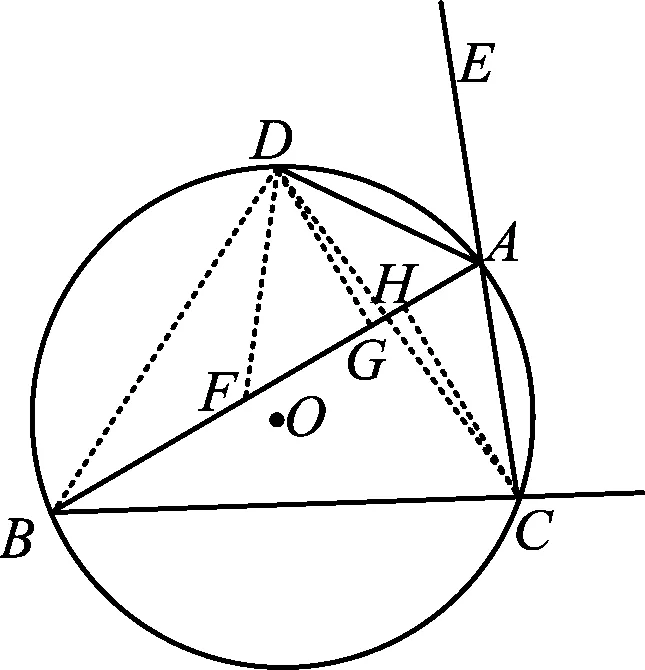
图8

DF=AD=5，AF=6，

且

AG=3，DG=4，BG=8，

故

即

BH=2CH，AH=11-2CH.

在Rt△AHC中，

25=(11-2CH)2+CH2，

可得

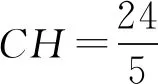
即

于是

解法延续第1)小题的思维自然生成，类比解法中“割出”的思路，还可以通过旋转甚至“补形”，做到思维再延续．

解法2如图9，将△DAC绕着点D顺时针旋转，使点C与点B重合，设点A落在AB上的点G处，联结DG，作GH⊥AD于点H，则

图9 图10

BG=AC=GD=AD=5，AG=6，

从而

∠BAC=∠GDA，

同上可得

解法3如图10，在射线CA上截取AG=6，联结DG，作GH⊥AD于点H，则CG=AB=11.又

CD=BD， ∠DCG=∠DBA，

从而

△DCG≌△DBA，

即

DG=AD=5， ∠BDA=∠CDG，

于是

∠BAC=∠BDC=∠ADG．

在Rt△ADG中，

可得

这些解法都延续“BD=DC，∠ABD=∠ACD”而成，通过全等三角形把已知的数学关系集中到一个图形中，进而解决问题．延续这些解法的更优化形式是直接利用等角或倍角关系构造等腰三角形或相似三角形．

3.2.2 构造等腰三角形

延续第1)小题发现的倍角关系，可构造等腰三角形.

解法4如图11，在AB上取一点G，使得∠BDG=∠DBG，则∠DGA=∠GAD，从而BG=DG=AD=5，AG=6，∠BAC=∠ADG.利用勾股定理可得

图11

故

解法5如图12，截取∠BCG=∠B交AB于点G，作CH⊥AB于点H.因为∠ACB=3∠B，所以

图12 图13

∠ACG=∠AGC=2∠B，

即

AG=AC=5，BG=CG=6.

由

25-AH2=36-(5-AH)2,

解得

故

3.2.3 构造相似三角形

延续第2)小题发现的∠ADC=∠ACD构造相似三角形.

解法6如图13，联结BD,CD，作CH⊥AB于点H，设CD交AB于点F，则△ADF∽△ABD，从而

即

故

3.2.4 利用三角函数倍角公式

延续图3的思维过程，融合二倍角关系，可以检测学有余力的学生的高级思维能力和创新能力，解法如下：

解法7如图14，点G在⊙O上，且DG=DA，作OP⊥GD于点P，交AB于点Q.作DM⊥AB于点M，则

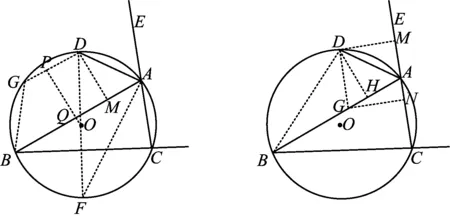
图14 图15

从而

AM=3，DM=4，

故

又DF是直径，则

∠DAF=90°=∠DAM+∠BAF，

故

因为 sin∠BAC=sin2∠BAF

则

所以

巧用二倍角和角平分线的性质定理构造矩形，过程如下：

解法8如图15，作DH⊥AB于点H.设AH=x，因为∠DAH=2∠DBH，所以

代入化简得

x2-11x+24=0，

解得

x=3(x=8舍去)，

故

AH=3，DH=4．

作DG∥CE交AB于点G，分别过点D，G作DM⊥EC，GN⊥EC，垂足为M，N，则

GA=GD=MN，GN=DM=DH=4.

设AN=y，则

AG=y+3，

在Rt△ANG中,

y2+16=(y+3)2，

得

故

延续图14，利用对称性构造倍角，整合相似三角形的性质，能把问题解决思路带到新高度：

解法9如图16，联结DO并延长交BC于点G，则DG⊥BC.设CD交AB于点F，FC=5x，则

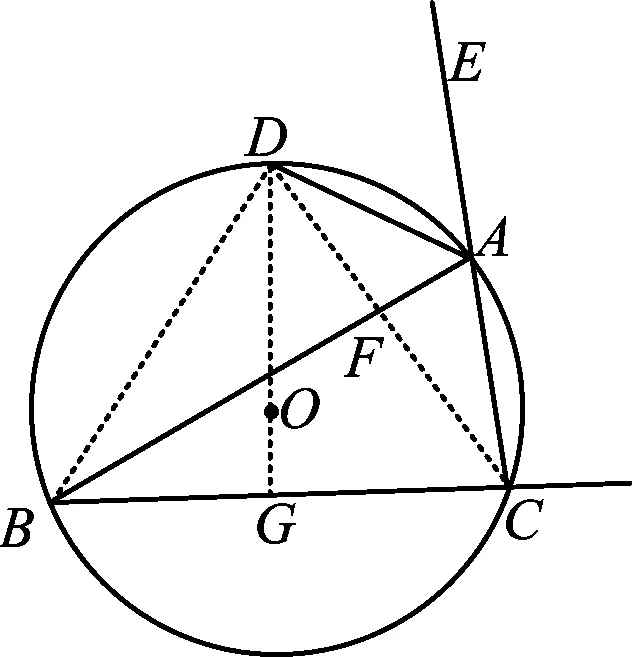
图16

△CBF∽△ABD，

故

BC=11x，

即

同理，设DF=5y，则

BD=11y，

从而

11y=5x+5y，

即

于是

即

从而

故

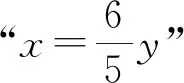
3.2.5 托勒密定理与方程组

解法10设BD=x，BC=y，易知∠BAC=∠BDC，由余弦定理得

(1)

由托勒密定理得

AB·CD=AD·BC+AC·BD,

(2)

将式(2)代入式(1)，得

故

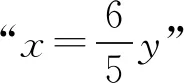
解法11如图17，作BH⊥CD于点H，由托勒密定理得

图17

由对称性得

故

因为BH·CD=BC·DG，所以

即

故

由上可知，第2)小题起点虽高，但在第1)小题的解法引导下，融合知识间的联系，运用思维的再延续，依然可以做到“百花齐放，百家争鸣”．

4 思考

1)思维延续性试题有利于培养学生的数学思维能力和问题解决能力.

试题是分辨学生解决问题能力强弱的试剂，好的试剂能检测到学生问题解决从尝试到完成的全过程.当这个过程符合学生的认知发展规律，能促使学生不断探索、发现、创造时，试题具备了思维的延续性和深刻性，这样的试题有利于培养学生的数学思维能力和问题解决能力．

2)问题解决教学应注意归纳、提炼问题解决过程中的思维延续的方法.

数学之难，很多时候就是“解题之难”．学生解题经验的积累不外乎两个方面：第一，从其所能开始，从所能做出回应的信息开始，不断积累经验；第二，延续所能作答的问题的思维末端继续探寻问题中新的数学关系，获得更丰富的经验和灵感．因此，学生在已有认知的基础上不断深入探析新的数学关系，不断尝试新的思维路径，在挫折和困境中获得真实的解题体验，并及时归纳、概括和总结其中的方法和思想，其本质就是运用思维的延续性感受真实的问题解决情境，培养创造性思维．